
Тема 4_векторный анализ (теория поля)
.pdf
|
|
|
|
|
|
|
|
|
Вариант №11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1. |
Найти вектор напряженности электрического поля, потенциал которого |
||||||||||||||||||||||||||||||||||||
имеет вид (r) arcsin |
1 |
, где r |
радиус-вектор точки, |
r |
|
r |
|
|
. Построить по- |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
r |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
верхности равного потенциала для случаев , |
|
|
, |
. |
|
|
|
|
|||||||||||||||||||||||||||||
|
Найти производную поля f x, y,z x3y2 z |
6 |
|
|
4 |
|
|
|
|
3 |
|
|
|
|
|||||||||||||||||||||||
2. |
в направлении градиента функ- |
||||||||||||||||||||||||||||||||||||
ции x,y,z x2 4x y 5y 6z2 в точке M 3,1, |
13 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
3. |
Показать, что поле вектора |
|
|
|
|
3y |
|
4x3 |
1 |
|
|
2x4 |
|
|
|
2 |
|
4 |
по- |
||||||||||||||||||
à |
|
|
|
|
|
|
i |
|
|
|
|
|
|
3y |
|
j 5z |
k |
||||||||||||||||||||
|
x4 |
y2 |
|
|
|
y3 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
||||||||
тенциально. Найти потенциал поля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4. |
Найти векторные линии поля вектора a x y2 z2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
i y j zk . |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5. |
Вычислить работу силы F x i |
|
|
|
|
|
j yk |
при перемещении по замкнуто- |
|||||||||||||||||||||||||||||
|
3 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
9 y |
2 |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
му контуру 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
z 2x y 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6. |
Вычислить поток поля |
a |
|
|
y z |
|
j |
x y k |
через часть поверхности |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
y |
z2 x2 , лежащую в I октанте и отсеченную плоскостью y 3, в направле- |
||||||||||||||||||||||||||||||||||||
нии внешней нормали. |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7. |
|
|
|
|
|
|
|
y |
2 |
|
z |
2 |
k |
|
|
через замкнутую поверхность, огра- |
|||||||||||||||||||||
Найти поток поля a x |
i |
|
|
j |
|
|
|
|
|||||||||||||||||||||||||||||
ничивающую область |
x2 y2 2, |
в направлении внешней нормали. |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 z y2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8. |
Проверить формулу Стокса для поля вектора a 4x2 y x2 |
||||||||||||||||||||||||||||||||||||
i 4 y2 |
j zk , |
||||||||||||||||||||||||||||||||||||
принимая за контур интегрирования окружность x2 y2 a2, z 0, а за поверх-
ность интегрирования – часть поверхности цилиндра x2 y2 a2, |
0 z 4 и |
||
z 4. |
|
|
|
9. Найти div grad f r , где |
r2 x2 y2 z2 , а f r произвольная дважды |
||
дифференцируемая функция от r. |
|
||
10. Найти a , если a |
с |
, c y,z,x , r2 x2 y2 z2. |
|
sin r |
|
||
|
|
|
|
11

|
|
|
|
Вариант №12 |
|
||
1. |
Найти вектор напряженности электрического поля, потенциал которого |
||||||
|
|
|
|
|
|
||
имеет вид (x, y,z) |
|
x2 y2 |
. Построить эквипотенциальные поверхности для |
||||
|
z |
||||||
случаев 0, 1. |
|
|
|
|
|||
|
|
|
|
|
|||
2. |
Найти производную поля u(x,y,z) arctg |
y |
xz |
в точке M 2, 2, 1 по |
|||
|
|||||||
|
|
|
|
|
x |
|
|
направлению нормали к поверхности x2 y2 2z 10, образующей острый угол с положительным направлением оси OZ .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5z |
3 |
|
|
|
|
|
2 |
|
|
||
3. |
Показать, что поле вектора |
а 4x3ey |
|
i x4 ey |
1 j |
15z |
1 k по- |
||||||||||||||||||||||
2 |
|
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
тенциально. Найти потенциал поля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4. |
Найти векторные линии поля вектора a z y |
i z 3 |
j y 3 |
k . |
|||||||||||||||||||||||||
5. |
Вычислить работу вектора силы F yi x j zk |
при перемещении по за- |
|||||||||||||||||||||||||||
|
2 |
y |
2 |
z |
2 |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
мкнутому контуру x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Вычислить поток поля a |
2 |
|
x 4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
6. |
|
i z j 6 k через часть поверхности |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 z2 4, лежащую в IV октанте, в направлении внешней нормали. |
|||||||||||||||||||||||||||||
7. |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
через замкнутую поверхность, ограни- |
||||||||||||||
Найти поток поля a x |
|
|
i y j 2zk |
|
|||||||||||||||||||||||||
|
|
x |
2 |
y |
2 |
|
6 y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
чивающую область |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
в направлении внешней нормали. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
0 z |
|
|
|
|
x2 |
y2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y z |
2 |
|
2 |
|
|
2 |
k , при- |
Проверить формулу Стокса для поля вектора a |
i zx |
|
j x y |
|
|||||||||||||||||||||||||
нимая за контур интегрирования окружность x2 y2 |
9, |
z 1, а за поверхность |
|||||||||||||||||||||||||||
интегрирования – часть параболоида x2 y2 9z, натянутого на этот контур.
|
|
|
|
|
|
|
|
d f |
|
|
r |
|
|
||
9. |
Доказать, что c |
|
|
d r |
|
|
, где c |
, r f r , c - постоянный вектор, |
|||||||
|
r |
||||||||||||||
r - радиус-вектор точки, |
r |
|
r |
|
, |
f r - произвольная дифференцируемая функ- |
|||||||||
|
|
||||||||||||||
ция от r. |
|
|
|
|
|
|
|
|
|
a , если r - радиус-вектор точки, |
|||||
10. |
Для поля вектора a r3 r . Найти a, |
||||||||||||||
r |
|
|
r |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12

Вариант №13
1. Потенциальная энергия частицы задана функцией u x,y,z arccos
Найти силу F , действующую на частицу. Какой вид имеют эквипотенциальные поверхности поля, в котором находится частица? Изобразить эти поверхности в случае
2. |
Найти производную поля f(x, y,z) x y3z4 |
в направлении градиента функ- |
||||||||||||||||||||||||||||||||||||
ции x, y,z x3 4x2y 5z2 3в точке M -1,21,-1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3. |
Показать, что поле вектора |
|
|
|
|
y z4 z4 |
|
|
|
z y |
|
|
|
|
5 |
|
|
|
4y z3 |
z y |
||||||||||||||||||
|
à |
|
|
i |
|
|
|
ze |
|
|
6 y |
|
|
j |
|
|
|
ye |
k |
|||||||||||||||||||
|
x2 |
|
x |
|
|
|
|
x |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
потенциально. Найти потенциал поля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
j |
|
|
|
|
|
k |
|
|
|
|
|
|
|
4. |
Найти векторные линии поля вектора a |
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||
x 3 |
y 4 |
z 9 |
|
|
|
|
||||||||||||||||||||||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
при переме- |
|||||
Вычислить работу силы F y z x2 |
i xz y |
|
j x y z2 |
k |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
y |
2 |
9, |
лежащей в I октанте, от точки A 3,0,0 |
к |
|||||||||||||||||||||||||||
щении по окружности x |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
z 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точке B 0,3,0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6. |
Вычислить поток поля a x y |
i y j zk |
через плоский треугольник с |
|||||||||||||||||||||||||||||||||||
вершинами в точках A 2,0,0 , B 2,0,4 , |
C 2, 2, |
0 . В направлении оси OX . |
||||||||||||||||||||||||||||||||||||
7. |
Найти поток поля a x z |
i x y j z y |
k |
|
через замкнутую поверх- |
|||||||||||||||||||||||||||||||||
ность, ограничивающую областьx2 y 2 z 23 |
3 |
|
|
, в направлении |
||||||||||||||||||||||||||||||||||
|
x2 y2 |
|||||||||||||||||||||||||||||||||||||
внешней нормали. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8. |
Проверить формулу Стокса для поля вектора |
|
2 |
|
|
|
z |
2 |
|
x |
2 |
y k , при- |
||||||||||||||||||||||||||
a |
y |
z i |
|
x j |
|
|||||||||||||||||||||||||||||||||
нимая за контур интегрирования окружность x2 y2 |
4, |
|
|
z 2, а за поверхность |
||||||||||||||||||||||||||||||||||
интегрирования – круг, ограниченный этой окружностью. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
9. |
Доказать, что div f r r 3 f r r |
dd rf , где r |
радиус-вектор точки, |
|||||||||||||||||||||||||||||||||||
r |
|
|
r |
|
, f r произвольная дифференцируемая функция от r. |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
10. Для поля вектора a r3c |
найти rot a,если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
r |
2 |
x |
2 |
y |
2 |
z |
2 |
, |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c 2xi |
y |
x j z k. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
13

Вариант №14
1. Потенциальная энергия частицы задана функцией u x,y,z 2x2 y2 z2.
Найти силу F , действующую на частицу. Какой вид имеют эквипотенциальные поверхности поля, в котором находится частица? Изобразить эти поверхности в случае u 0, u 1, u 2.
2. Найти производную скалярного поля u(x,y,z) ln 1 x2 y2 
 x2 z2 в
x2 z2 в
точке M 0,0,5 по направлению нормали к поверхности x2 6x 9y2 z2 4z 5,
образующей острый угол с положительным направлением оси OZ .
3. |
Показать, что поле вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à y4 zxz 1 2 yxy 1 i 4x y3 2xy lnx |
j xz ln x 1 k |
||||||||||||
потенциально. Найти потенциал поля. |
|
|
|
|
|
|
|
|
|
|
||||
4. |
Найти векторные линии поля вектора a y 2 i x 2 j z k . |
|||||||||||||
|
|
|
1 |
|
1 |
|
x |
|
y |
|
||||
5. |
Показать, что поле вектора a |
|
|
|
i |
|
|
|
|
|
|
j |
|
k является потенциаль- |
y |
|
|
z2 |
|||||||||||
|
|
|
|
z |
|
y2 |
|
|
||||||
ным и вычислить линейный интеграл этого вектора от точки A 2, 3, 1 до точки B 4,6,2 .
6. Вычислить поток поля a x z i x j y k через часть поверхности
z2 x2 4, лежащую в IV октанте и отсеченную плоскостями y 3, |
y 1, в |
направлении внешней нормали. |
|
7. |
Найти поток поля a z i x y j yzk |
через часть поверхности |
y z2 x2 4, отсеченную плоскостью y 2, |
в направлении внешней нормали. |
|
8. |
Проверить формулу Стокса для поля вектора a y z i z j yk , прини- |
|
мая за поверхность интегрирования – поверхность, лежащую в I октанте, ограниченную параболоидом y 9 x2 z2 и плоскостями x 0, z 0, а за линию интегрирования – линию пересечения этой поверхности с плоскостью y 0.
9. Доказать, что rot rota grad diva a.
10. Найти a, a , для вектора a r sin2 r , где r радиус-вектор точки, r r .
Вариант №15
1.Найти вектор напряженности электрического поля, потенциал которого задан функцией (M) x2 3y2 z2. Построить поверхности равного уровня для случаев 0, 1, 2.
2.Найти производную скалярного поля u(x, y,z) 
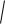 x2 y2 z в точке
x2 y2 z в точке
M 3, 4, 1 по направлению нормали к поверхности x2 y2 25z,образующей острый угол с положительным направлением оси OZ .
3. Показать, что поле вектора
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à y zxy 1 1 i 5z y4 xyzln x 2y |
j y5 xy 3z2 k |
|||||||||||||||||
потенциально. Найти потенциал поля. |
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
4. |
|
|
|
|
|
|
|
|
|
|
z |
x |
|||||||||
Найти векторные линии поля вектора a z i |
|
j x k . |
|||||||||||||||||||
5. |
Вычислить циркуляцию вектора a y i x j z k |
по контуру, составлен- |
|||||||||||||||||||
ному из осей координат и дуги кривой x a cos3t, |
y a sin3t |
между точками |
|||||||||||||||||||
A a,0,1 и B 0,a,1 в плоскости z 1. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||
6. |
Найти поток поля a y i x |
|
|
k через часть поверхности |
|||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
z2 x2, лежащую в IV октанте и отсеченную плоскостями y 2, в |
|||||||||||||||||||
направлении внешней нормали. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7. |
Найти поток поля a y i x j z k |
через замкнутую поверхность, ограни- |
|||||||||||||||||||
|
|
|
|
|
2 |
y |
2 |
4, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
в направлении внешней нормали. |
|||||||||||||||
чивающую область |
0 z 8 x, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
Проверить формулу Стокса для поля вектора a yz i xz 4x j x y k , |
||||||||||||||||||||
принимая за контур интегрирования эллипс 4x2 y2 4, |
|
|
z 0, а за поверхность |
||||||||||||||||||
интегрирования – часть поверхности цилиндра |
|
|
2 |
y |
2 |
4, |
и плоскости z 2. |
||||||||||||||
4x |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 z 2, |
|
|
||||||
9. |
Показать, что любое решение уравнения a k2 a 0, удовлетворя- |
||||||||||||||||||||
ющее условию соленоидальности, удовлетворяет векторному уравнению |
|||||||||||||||||||||
Гельмгольца 2 a k2 a 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10. Вычислить rot a и diva, где a yzi 2xz j |
cosr, |
r2 x2 y2 z2. |
|||||||||||||||||||
15

Вариант №16
1. Найти вектор напряженности электрического поля, потенциал которого равен функцией (M) x2 2x 1 4z2 4 y . Построить эквипотенциальные по-
верхности для случаев 0, |
4. |
|
|
|
|
|
|
|
|
|
|
|
|
z y |
|
|
|
|||||||||||
2. |
Найти производную скалярного поля u(x,y,z) x |
|
|
|
|
в точке |
||||||||||||||||||||||
|
y |
x |
||||||||||||||||||||||||||
M 1, 1, 2 по направлению нормали к поверхности x2 y2 z2 |
4, образующей |
|||||||||||||||||||||||||||
острый угол с положительным направлением оси OZ . |
|
|
|
|
|
|
|
|
||||||||||||||||||||
3. |
Показать, что поле вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
10x4 |
z |
|
|
|
2x5 |
|
|
|
2 y |
|
y |
|
|
y2 |
|||||||||||
|
à |
|
y |
i |
|
|
|
|
|
|
|
|
z |
j |
|
|
1 |
|
|
k |
||||||||
|
|
|
|
|
y2 |
|
1 y2z2 |
|
|
|||||||||||||||||||
|
|
|
1 y2z2 |
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
||||||||||
потенциально. Найти потенциал поля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4. |
Найти векторные линии поля вектора a y 2 i x 2 |
|
j z 2 k . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
2 |
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
5. |
Вычислить работу силы F |
|
|
i |
|
|
j x yk |
при перемещении по дуге |
||||||||||||||||||||
z |
|
|
|
|
||||||||||||||||||||||||
окружности x2 y2 1, |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z 1, расположенной в I октанте между точками |
||||||||||||||||||||||||||||
A 1, 0,1 и B 0,1,1 .
6.Вычислить поток поля a y, x, z через часть поверхности
x2 y2 z2 R2, лежащую в III октанте, в направлении внешней нормали.
|
x |
2 |
|
|
через полную поверхность пирами- |
|||||
7. Найти поток поля a |
|
i x y j 3zxk |
||||||||
ды с вершинами в точках A(4, 0, 0), B 0, 2, |
0 , C 0, 0, |
4 , O 0,0,0 |
в направле- |
|||||||
нии внешней нормали. |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
8. Проверить формулу Стокса для поля вектора a z i x j x y |
|
k , прини- |
||||||||
мая за контур интегрирования окружность x b cost, |
y 0, |
z b sint,а за по- |
||||||||
верхность интегрирования – поверхность конуса с высотой H , натянутую на |
||||||||||
этот контур. |
|
|
|
a, r , где r радиус-вектор точки поля, |
||||||
9. Доказать, что r r, a 4 |
||||||||||
a заданный постоянный вектор.
10. Найти rot a f r , где a |
y i 2 j xzk , |
f r произвольная дифференци- |
руемая функция, a r2 x2 y2 z2. |
|
|
16

Вариант №17
1. Потенциальная энергия частицы задана функцией
u x,y,z x2 2x 1 3z2 9 y. Найти силу F , действующую на частицу. Какой вид имеют эквипотенциальные поверхности поля, в котором находится части-
ца? |
Изобразить эти поверхности в случае u 0, u 9. |
|
|
||
2. |
Найти производную скалярного поля u(x, y,z) |
|
|
4 z2 в точке |
|
x y |
|||||
M 1, 1, 0 по направлению нормали к поверхности z x2 y2 , образующей ту-
пой угол с положительным направлением оси OZ .
3. |
Показать, что поле вектора |
|
|
|
|
|
||||||
|
|
|
|
|
3 |
|
|
|
3x |
|
|
|
|
à |
|
yzsin x i |
|
|
|
i zcosx 1 |
j |
ycosx |
|
1 k |
|
|
z |
z2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
потенциально. Найти потенциал поля. |
|
|
|
|
|
|||||||
4. |
Найти векторные линии поля вектора a y z 1 i x z 1 |
j x yk . |
||||||||||
5.Вычислить работу силы F y z2i x2y j y2xk при перемещении по пря-
мой из точки A 2, 3, 1 и B 4, 6, 2 . |
|
|
|
|
||||||
6. |
Вычислить поток поля a x y |
i z y j x y k через плоский тре- |
||||||||
угольник с вершинами A 6,6,0 , B 6,6,0 , |
C 0,6,6 в направлении оси OY . |
|||||||||
7. |
Найти поток поля a 75 x3 |
|
|
|
|
|
через замкнутую поверхность, |
|||
i y3 |
j z3k |
|||||||||
|
|
x |
2 |
y |
2 |
x, |
|
|
||
|
|
|
|
|
|
|||||
ограничивающую область |
|
|
|
|
|
|
|
|
в направлении внешней нормали. |
|
|
|
|
|
|
y2 , |
|
||||
|
0 z x2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
8.Проверить формулу Стокса для поля вектора a 3y2 i 3z2 j 3x2 k , принимая за поверхность интегрирования поверхность, лежащую в I октанте, ограниченную сферой x2 y2 z2 4 и плоскостями x 0, y 0, а за линию интегрирования – линию пересечения этой поверхности с плоскостью z 0.
9.Доказать, что в потенциалом поле вектора a его потенциал u(x, y,z) удовлетворяет уравнению Пуассона u a .
10. Найти rot a и diva для вектора a rsinr r , |
r |
|
r |
|
, r радиус-вектор |
|
|
||||
точки. |
|
|
|
|
|
17
Вариант №18
1. Потенциальная энергия частицы описывается функцией
u M x2 2x 2 y2 4 y 4z2 16z 15 . Найти силу F , действующую на частицу.
Какой вид имеют эквипотенциальные поверхности поля, в котором находится частица? Изобразить эти поверхности в случае
|
Найти производную скалярного поля u(x, y,z) x2 y2 z2 |
3 |
|
|
||||
2. |
2 в точке |
|
||||||
M 1, 1, 0 по направлению нормали к поверхности заданной уравнением |
|
|||||||
2x2 y2 z2 1. |
|
|
|
|
|
|
|
|
3. |
|
4x3 |
|
|
3x4 |
|
|
|
Показать, что поле вектора à |
z3 |
i zcos y 1 |
j sin y |
z4 |
2z k по- |
|||
|
|
|
|
|
|
|
||
тенциально. Найти потенциал поля. |
|
|
|
|
|
|
4. |
Найти векторные линии поля вектора a 1 z i y j x 1 k . |
|
||||
5. |
Вычислить циркуляцию ротора вектора |
F y z2 |
|
|
2yk |
по контуру, |
i |
x2z j x |
|||||
состоящему из дуги параболы y x2 и отрезка прямой y x в плоскости z |
0. |
6. Найти поток поля a y i x j z k через часть поверхности z 4 2 x2 |
16, |
лежащую во II октанте и отсеченную плоскостями y 0, y 2, в направлении внешней нормали.
7. Вычислить поток поля a x y i xz j z k через часть поверхности
z 4 x2 y2 отсеченную плоскостью z 2, в направлении внешней нормали. 8. Проверить формулу Стокса для поля вектора a y i x j x y k , прини-
мая за поверхность интегрирования поверхность, лежащую во II октанте, ограниченную сферой с центром в начале координат радиуса a и плоскостями y 0, z 0, а за контур интегрирования – линию пересечения этой поверхности с плоскостью x 0.
9. |
|
|
|
2 |
|
|
|
|
Доказать, что |
, (x, y,z)- дважды дифференциру- |
|||||||
емая функция. |
|
|
|
|
|
|
|
|
10. |
Найти rot a и diva для вектора a r b cosr , где r |
|
r |
|
, r - радиус- |
|||
|
|
|||||||
вектор точки, b - постоянный вектор.
18

Вариант №19
1. Найти вектор напряженности электрического поля, потенциал которого
описывается функцией (x, y,z) |
3 |
. Построить эквипотенциальные по- |
|
x2 y z2 |
|||
|
|
верхности для случаев 1, 2.
2. Найти производную скалярного поля u(x, y,z) 4ln 3 y2 8x y z в точке
M 1, 1, 1 по направлению нормали к поверхности x2 2 y2 2z2 1, образующей
тупой угол с положительным направлением оси OZ . 3. Показать, что поле вектора
à |
|
3 |
|
4y 5y |
|
|
|
|
4y |
2 |
|
|
ze4y |
3z4 |
i 4xz e |
4 |
j xe |
3z3 |
1 k |
||||||
|
|
x |
|
|
|
|
|
|
|
x |
|
|
потенциально. Найти потенциал поля.
4.Найти векторные линии поля вектора a 1 z i x j y 1 k .
5.Вычислить работу силы a y z i xz j при перемещении по дуге винтовой
линии x Rcost, y Rsint, |
z |
4t |
от точки пересечения кривой с плоскостью |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 0 |
до точки её пересечения с плоскостью z 8. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
6. |
Вычислить поток поля |
a y 2 i |
|
|
z 2 k через часть поверхности |
|
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
z 2 |
x2 y2 , лежащую во II октанте, в направлении внешней нормали. |
|
||||||||||||||||||||||||||||
7. |
Найти поток поля |
|
|
|
|
2 |
|
|
через замкнутую поверхность, ограни- |
|||||||||||||||||||||
|
a x |
|
i y j z k |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
y |
2 |
2 y, |
в направлении внешней нормали. |
|
|
|
|||||||||||||||
чивающую область x |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
0 z 4 y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
||||||
8. |
Проверить формулу Стокса для поля вектора a y z i |
xz |
|
|
x |
|
j x y k , |
|||||||||||||||||||||||
8 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
принимая за поверхность интегрирования боковую поверхность пирамиды, |
|
|||||||||||||||||||||||||||||
ограниченную плоскостями x 0, y 0, |
|
x 2 y 4z 8 |
z 0 , а за контур инте- |
|||||||||||||||||||||||||||
грирования – линию её пересечения с плоскостью z 0. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
9. |
Доказать, что rot |
c f r 1 d f r,c , где r |
|
r |
|
, |
r радиус-вектор точки, |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
d r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
c постоянный вектор, |
f r - произвольная дифференцируемая функция от r. |
|||||||||||||||||||||||||||||
10. Найти a и a |
|
для поля вектора a csin r , если c постоянный вектор, |
||||||||||||||||||||||||||||
r |
|
|
r |
|
|
, r радиус-вектор точки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
19
|
Вариант №20 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1. |
Найти вектор напряженности электрического поля, потенциал которого |
||||||||||||||||||||||||
описывается функцией (x, y,z) |
|
|
1 |
|
|
|
|
. Построить эквипотенциальные по- |
|||||||||||||||||
y |
2 z2 x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
верхности для случаев 1, 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
Найти производную скалярного поля u(x, y,z) ln ex ey ez |
в начале ко- |
|||||||||||||||||||||||
ординат по направлению луча, образующего угол 60 с осью абсцисс, |
угол 45 |
||||||||||||||||||||||||
с осью ординат, а с осью аппликат – тупой угол. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
z |
|
|
y |
|
5 |
|
|
y |
|
|||||
3. |
Показать, что поле вектора à |
|
|
|
|
|
|
i |
|
|
|
|
|
e |
|
|
|
|
j |
|
|
1 k по- |
|||
x y z |
|
y z |
|
|
|
||||||||||||||||||||
тенциально, найти потенциал поля. |
|
|
x |
|
|
|
y |
|
x y z |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. |
Найти векторные линии поля вектора a z 1 i z x |
j x 1 k . |
|||||||||||||||||||||||
|
|
|
|
|
|
z2 |
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
||||
5. |
Вычислить работу силы F z y i |
|
|
|
|
j |
|
|
|
|
k |
при перемещении вдоль ли- |
|||||||||||||
|
x |
|
|
x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нии (L): x = 4, x 4, y2 z2 16 от точки A 4, 4, 0 |
к точке B 4, 0, 4 . |
|
|||||||||||||||||||||||
6.Вычислить поток поля a x3 i j k через часть поверхности
x2 y2 z2 1, лежащую в IV октанте, в направлении внешней нормали.
|
|
2 |
|
|
|
|
|
|
|
|
|
|
7. Найти поток поля a 6x y i 3y |
j 5 k через полную поверхность пира- |
|||||||||||
миды с вершинами в точках A 2,0,0 , B 0,1,0 , C 0,0, 1 , |
|
D 0,0,0 |
в направ- |
|||||||||
лении внешней нормали. |
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
y |
z |
z |
y k , при- |
|||||||
8. Проверить формулу Стокса для поля вектора a |
|
i |
|
x j x |
|
|||||||
нимая за контур интегрирования окружность x2 y2 |
4, z |
2, а за поверхность |
||||||||||
интегрирования – поверхность кругового цилиндра |
|
2 |
y |
2 |
4, |
натянутую на |
||||||
x |
|
|
||||||||||
эту окружность, и плоскость z 0. |
|
0 z 2, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
9. Доказать, что вектор div u gradv u v gradu, gradv , где u u(õ,y,z), |
||||||||||||
v v(õ, y,z) произвольные дважды дифференцируемые функции. |
|
|
||||||||||
10. Вычислить rot r, a b , если a 2 i j , b 3 i 2 |
j k , r x i y j zk . |
|||||||||||
20
