
ИДЗ_Собственные значения и собственные векторы
.pdf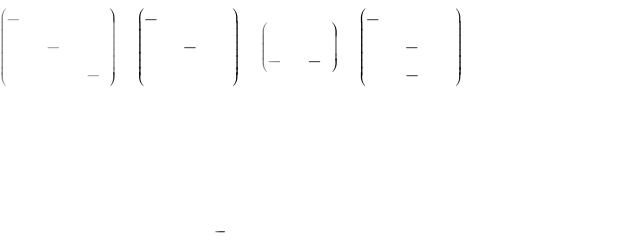
ИДЗ «Собственные значения. Собственные векторы»
Вариант 1
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному) виду и найти соответствующий базис.
3 |
5 |
0 |
|
1 |
0 |
0 |
5 |
4 |
|
1 |
2 |
0 |
0 |
3 0 |
, |
0 |
1 |
3 , |
, |
0 |
2 |
0 . |
|||
0 |
2 |
3 |
|
0 |
0 |
2 |
9 |
8 |
|
8 |
4 |
3 |
|
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
2 |
(1, 0, 1) |
2 |
(1, 1, 1) |
4 |
(1, 1, 0) |
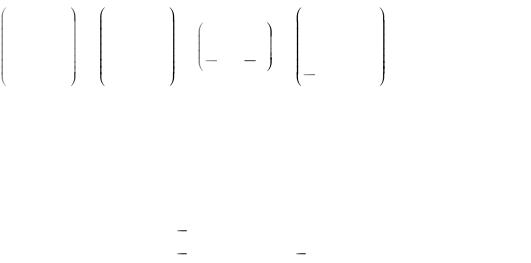
Вариант 2
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному) виду и найти соответствующий базис.
9 |
0 |
0 |
2 |
0 |
0 |
6 |
9 |
|
0 |
4 |
0 |
2 |
9 |
0 , 0 |
2 |
3 , |
, |
0 |
2 |
0 . |
|||
5 |
0 |
9 |
0 |
0 |
1 |
1 |
4 |
|
2 |
4 |
1 |
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
1 |
(2, 0, 1) |
|
1 |
(1, 1, 1) |
|
3 |
(2, |
1, 1) |
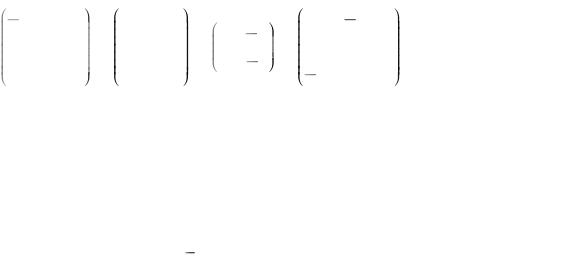
Вариант 3
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному)
виду и найти соответствующий базис.
4 |
0 |
0 |
9 |
0 |
0 |
8 |
9 |
|
2 |
2 |
0 |
0 |
2 |
1 , 0 |
1 |
0 , |
, |
0 |
3 |
0 . |
|||
0 |
0 |
2 |
2 |
0 |
1 |
2 |
1 |
|
2 |
4 |
1 |
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
2 |
(1, 0, 1) |
2 |
(1, 1, 1) |
4 |
(1, 1, 0) |

Вариант 4
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному)
виду и найти соответствующий базис.
5 |
0 |
0 |
7 |
0 |
0 |
2 |
9 |
|
2 |
0 |
4 |
6 |
5 |
0 , 2 |
3 |
0 , |
, |
6 3 |
12 . |
||||
0 |
0 |
8 |
0 |
0 |
3 |
1 |
8 |
|
0 |
0 |
1 |
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
1 |
(3, 0, 1) |
1 |
(0, 1, 0) |
4 |
(2, 0, 1) |
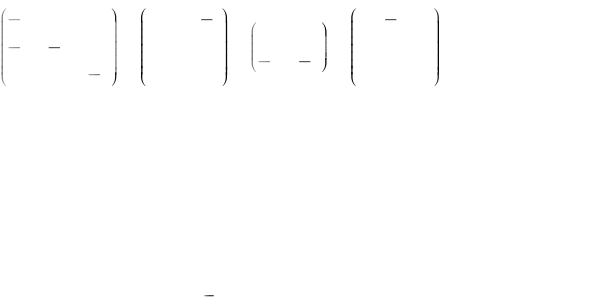
Вариант 5
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному)
виду и найти соответствующий базис.
6 |
0 |
0 |
3 |
0 |
1 |
|
2 |
1 |
1 |
2 |
0 |
3 |
6 1 |
, 0 |
6 |
0 |
, |
, 0 |
2 |
0 . |
|||
0 |
0 |
6 |
0 |
0 |
6 |
|
7 |
6 |
4 |
4 |
3 |
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
2 |
(1, 1, 5) |
2 |
(0, 1, 1) |
1 |
(1, 0, 5) |
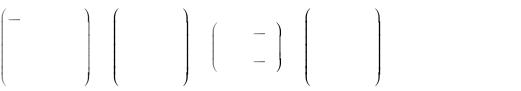
Вариант 6
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному)
виду и найти соответствующий базис.
8 |
0 |
0 |
3 |
0 |
0 |
10 |
4 |
1 |
0 |
0 |
0 |
7 |
5 , 0 |
3 |
0 , |
, 0 |
1 |
0 . |
|||
0 |
0 |
7 |
0 |
1 |
4 |
6 |
1 |
2 |
0 |
2 |
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
2 |
(2, 3, 0) |
3 |
(1, 2, 1) |
4 |
(0, 1, 1) |
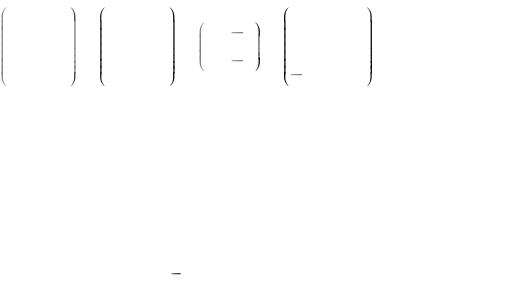
Вариант 7
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному)
виду и найти соответствующий базис.
1 |
4 |
0 |
2 |
0 |
0 |
3 |
7 |
|
1 |
2 |
0 |
0 |
1 |
0 , 0 |
2 |
0 , |
, |
0 |
2 |
0 . |
|||
0 |
0 |
3 |
3 |
0 |
5 |
1 |
5 |
|
4 |
8 |
3 |
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
1 |
(3, 1, 1) |
2 |
(1, 1, 0) |
4 |
(3, 0, 1) |
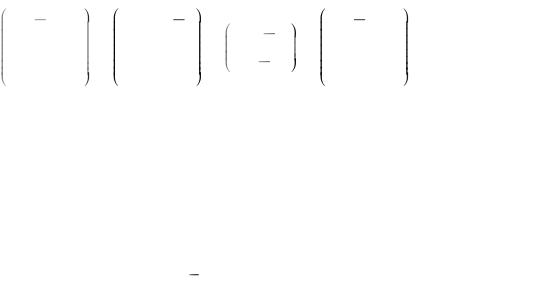
Вариант 8
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному)
виду и найти соответствующий базис.
1 |
2 |
4 |
1 |
0 |
4 |
|
8 |
9 |
0 |
4 |
0 |
0 |
1 |
0 , 0 |
1 |
0 |
, |
, 0 |
2 |
0 . |
|||
0 |
0 |
1 |
0 |
0 |
2 |
|
4 |
10 |
2 |
8 |
1 |
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
2 |
(1, 0, 1) |
2 |
(1, 1, 1) |
4 |
(1, 1, 0) |
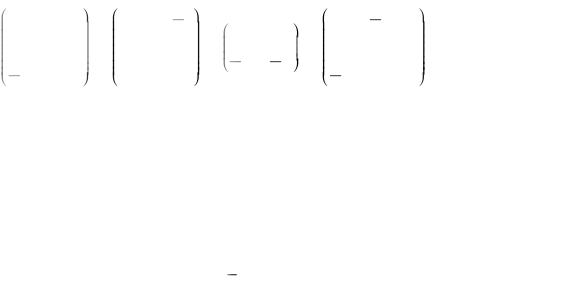
Вариант 9
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному)
виду и найти соответствующий базис.
7 |
0 |
0 |
3 |
0 |
1 |
|
9 |
6 |
|
2 |
2 |
0 |
0 |
7 |
0 , 0 |
6 |
0 |
, |
, |
0 |
3 |
0 . |
|||
1 |
3 |
7 |
0 |
0 |
6 |
|
4 |
2 |
|
2 |
4 |
1 |
|
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
1 |
(4, 1, 2) |
1 |
(1, 1, 0) |
4 |
(2, 0, 1) |
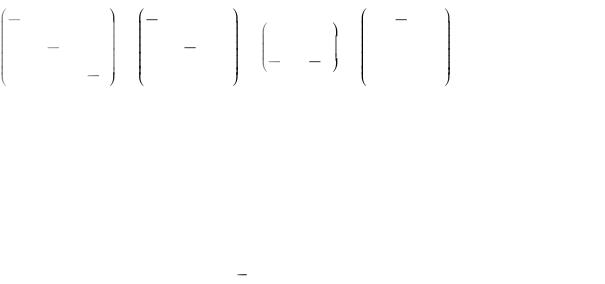
Вариант 10
Задание 1.
1.Найти собственные значения линейного оператора, заданного матрицей в некотором базисе.
2.Является ли оператор оператором простой структуры?
3.Найти собственные векторы линейного оператора, заданного матрицей в некотором базисе.
4.Привести матрицу линейного оператора к диагональному (клеточно-диагональному)
виду и найти соответствующий базис.
3 |
5 |
0 |
|
1 |
0 |
0 |
2 |
1 |
1 |
4 |
0 |
0 |
3 0 |
, |
0 |
1 |
3 , |
, 0 |
3 |
0 . |
|||
0 |
2 |
3 |
|
0 |
0 |
2 |
7 |
6 |
2 |
8 |
2 |
|
|
|
|||||||||
Задание 2.
Даны собственные значения и собственные векторы линейного оператора в некотором базисе. Найти матрицу оператора в этом базисе.
1 |
(3, 0, 1) |
1 |
(0, 1, 0) |
4 |
(2, 0, 1) |
