Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математический анализ ИДЗ №1 Введение в анализ

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1.16 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Уральский федеральный университет имени первого Президента России Б.Н.Ельцина» Институт радиоэлектроники и информационных технологий – РТФ

Кафедра Вычислительных методов и уравнений математической физики

Введение в анализ Сборник типовых заданий

Екатеринбург

УрФУ

2013

Белоусова В. И., Криковцева Т. Г., Михалева М. М., Шестакова И. А.

Введение в анализ: сборник типовых заданий/ В. И. Белоусова, Т. Г. Криковцева, М. М. Михалева, И. А. Шестакова. Екатеринбург: УрФУ, 2013. 34 с.

Приведены 30 вариантов индивидуальных заданий по теме «Введение в анализ» для студентов Института радиоэлектроники и информационных технологийРТФ

©Уральский федеральный университет, 2013 © Белоусова В. И., Криковцева Т. Г., Михалева М. М., Шестакова И. А., 2013

Указания к оформлению контрольных работ

При выполнении контрольной работы (индивидуального домашнего задания, расчетно-графической работы) студенту необходимо руководствоваться следующим:

1.Номер варианта контрольной работы определяется порядковым номером в списке по журналу группы и остается неизменным в течение учебного года.

2.Контрольные работы выполняются в обычной школьной тетради (12-18 листов), на обложке которой приводятся сведения по следующему образцу:

Институт радиоэлектроники и информационных технологий – РТФ Кафедра Вычислительных методов и уравнений математической физики

Т Е Т Р А Д Ь

		Контрольная работа № _
	По	(указать наименование дисциплины)
			(Указать номер варианта)
		(Название контрольного мероприятия)
	Студента(ки)		1 курса,	группы РИ- (номер)
	(указать ФИО студента в родительном падеже)
				Преподаватель (ФИО)

Дата сдачи работы _______
Оценка		_______	(Подпись преподавателя)

3.Условия задач в контрольной работе переписывать полностью, без сокращений. Весь ход решения задачи сопровождать краткими, но исчерпывающими пояснениями.

4.На страницах тетради оставляются поля для замечаний преподавателя. После каждой решенной задачи необходимо оставлять место для замечаний преподавателя и для ответа на эти замечания. Каждая следующая задача должна начинаться с новой страницы. Если контрольная работа при первой проверке не зачтена, то студент обязан представить ее исправленный вариант на повторную проверку в указанный срок (в этой же тетради), включив те задачи, решение которых оказалось неверным. Зачтенные задачи заново переписывать не надо. Если работа для повторной проверки переписана заново, то ее надо представлять вместе

суже проверенной работой.

5.Защита выполненных, но не зачтенных работ проводится во время зачетной недели в форме собеседования с преподавателем (в часы занятий и консультаций).

6.В том случае, когда работа зачтена, студенту возвращается только обложка работы

сотметкой преподавателя и его подписью.

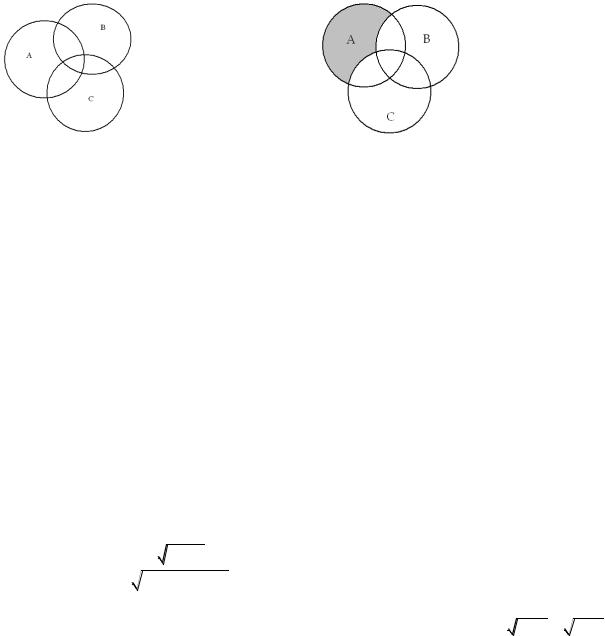
Индивидуальные задания по теме «Введение в анализ»

	Вариант 1
I.	Заштриховать ту часть II.	Записать множество,
	диаграммы на рис. 1,	изображенное с
	которая соответствует	помощью кругов
	множеству	Эйлера на рис. 2.
	(A B) (C \ B) .

Рис. 1	Рис. 2

III.Пользуясь определением равенства множеств, доказать, что

A \ (B C) (A \ B) (A \ C) .

IV. Пользуясь определением предела последовательности, доказать, что

lim	n 3	1	.
	2n 5	2
n

V.Исследовать на сходимость последовательность с общим членом


		a	1	1	1				1		.
		a									.
		n	1 2	2 3	3 4			n n 1
			1 2	2 3	3 4			n n 1
VI. Пользуясь определением предела функции, доказать, что
а) lim	x3 1	;		б) lim		3x2 2x 1				3 .
а) lim	x 1 2	;		б) lim		x2	1			3 .
x 1	x 1 2				x	x2	1

VII. Найти пределы, если они существуют:

2 4n2 3n3

а) lim

8sin(2n!

n4 7) 3n2

; б) lim

;

16n4 9n3 8

n3 7n 10

г) lim tg x 2 x

;

д) lim

1 cos 6x

;

x 0

x sin 3x

x 2

в)

е)

	2x 5		5 x
lim				;
	2x 1
x
lim		x2 x 12			.

		x 2		4 x
x 3

VIII. Исследовать функции на непрерывность, установить характер точек разрыва:

		x2 1,		x 0;

		3			б) f (x)	1
а)	f (x)		, 0	x 2; ;				.
а)	f (x)		, 0	x 2; ;		1		.
	x 2
	x 2				2	x2	2
	2x 1,			x 2.	2		2
	2x 1,			x 2.

					4

	Вариант 2
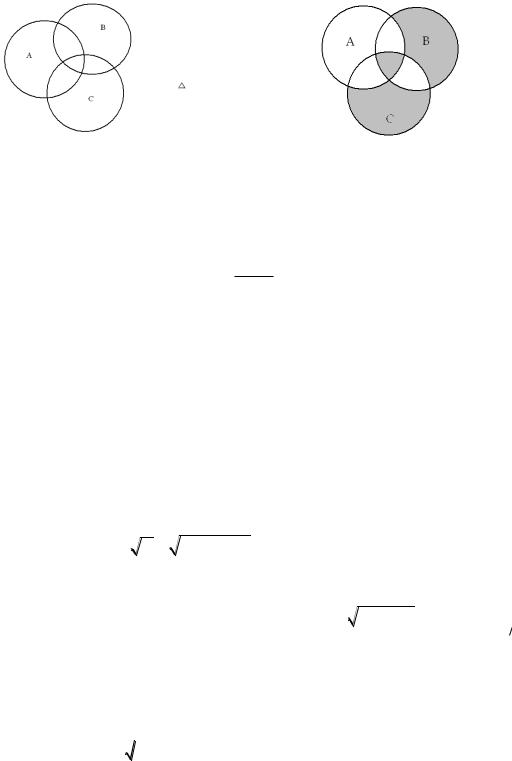
I.	Заштриховать ту	II.	Записать множество,
	часть диаграммы на		изображенное с
	рис. 3, которая		помощью кругов
	соответствует		Эйлера на рис. 4.
	множеству
	(A \ B) (B \ C) .

Рис. 3	Рис. 4

III.Пользуясь определением равенства множеств, доказать, что

A \ (B C) (A \ B) (A \ C) .

IV. Пользуясь определением предела последовательности, доказать, что

lim	5n2 n 2	.
	4n 2
n

V.Исследовать на сходимость последовательность с общим членом

n 1

n 2

n 3

VI. Пользуясь определением предела функции, доказать, что

a) lim

5x 1

;

б)

lim

(x2

3x 2)

3x2

2x 6 3

x 1

(x 1)2

VII. Найти пределы, если они существуют:

1 2

1 sin 3x

ctg x

а)

lim

;

б) lim

; в)

1 tg 5x

x 0

sin2 3x

г)

;

д) lim

;

е)

lim

n n 5

x 0 x arctg x

	x 2	3x 1
		x2
lim		;

x 0	2x 2

lim	x2	2x 1	.
		x3 x
x 1

VIII. Исследовать функции на непрерывность, установить характер точек разрыва:

x 1					,		x 1;

	x 3

	2			2					б) f x x sign x	3		2	2x .
а) f x =			x			,		1 x 2;			x
а) f x =	3		x			,		1 x 2;			x
	3
		3x 4,						x 2.


									5

	Вариант 3
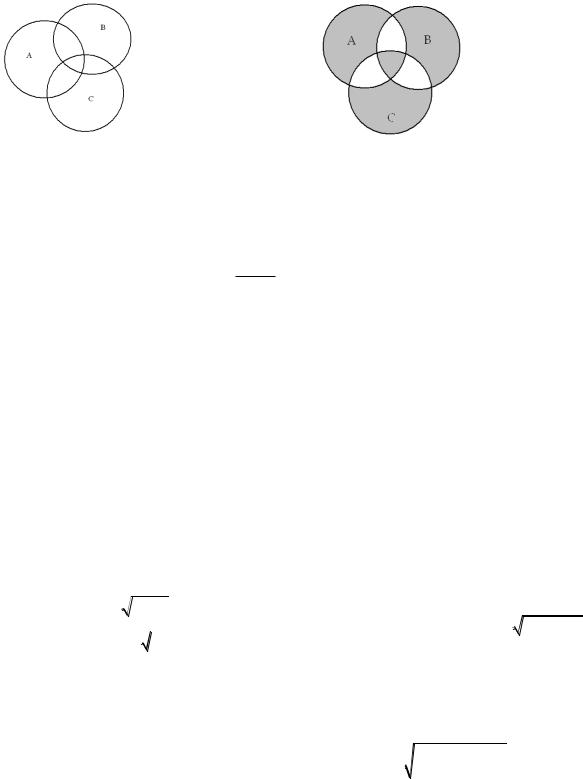
I.	Заштриховать ту	II.	Записать множество,
	часть диаграммы на		изображенное с
	рис. 5, которая		помощью кругов
	соответствует		Эйлера на рис. 6.
	множеству
	(A B) (C \ B).

Рис. 5	Рис. 6

III.Пользуясь определением равенства множеств, доказать, что

A (B \ C) (A B) \ ( A C) .

IV. Пользуясь определением предела последовательности, доказать, что

lim 2n 3 2 .

n n 2

V.Исследовать на сходимость последовательность с общим членом

n 2n 1

1 1

2 3

3 5

VI. Пользуясь определением предела функции, доказать, что

а) lim

1 x x2

1 ;

б)

lim

(x2

2x 3)

3 x2

(x 1)2

x 1

VII. Найти пределы, если они существуют.

arcsin 4x

6 x 1

а) lim

n4 sin

n! n10

8n 4

; б) lim

; в)

lim

6x 8

;

13n 4

ctg 2x arctg

6x 8

x 0

1 arcsin

x sin 2 x

8x3 1

г) lim

n2 n 1 ;

lim

;

д) lim

е)

6x 1

x 0

x 1 2 6x

VIII. Исследовать функции на непрерывность,

x2		2x, 3 x 1;
	x	2,	1 x 3;
а) f x =

		x2 7,	x 3.

установить характер точек разрыва:

б) f x	x 2		.



	x	1

	Вариант 4
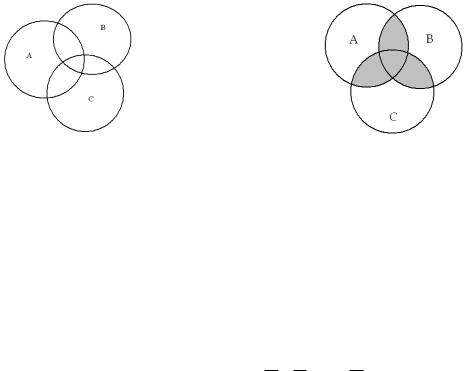
I.	Заштриховать ту	II.	Записать множество,
	часть диаграммы на		изображенное с
	рис. 7, которая		помощью кругов
	соответствует		Эйлера на рис. 8.
	множеству
	(A B) (C \ B).

Рис. 7	Рис. 8

III.Пользуясь определением равенства множеств, доказать, что

A (B \ C) (A B) \ C .

IV. Пользуясь определением предела последовательности, доказать, что

lim cos n2 0 .

n 2n

V.Исследовать на сходимость последовательность с общим членом

a 1

5n 1

VI. Пользуясь определением предела функции, доказать, что

а) lim

10x2 3x 1

;

б) lim

4x 3

5x2 1

x 3

VII. Найти пределы, если они существуют.

2 lg(10

1)sin

)

;

tg 5x sin 3x

а)

lim

б) lim

;

cos x sin x

cos 4x cos x

x 0

3 n 3 n4 5 sin

1 2x

ctg 3 x

г)

lim

;

д) lim

;

1 sin

x 0

в)

е)

	arctg x ctg x		;
lim
		x
x 0

lim 3 n3 n 7 n .

VIII. Исследовать функции на непрерывность, установить характер точек разрыва:

1 2x,

1 x 1;

x 1

x 3

б) f x

а) f (x)

1 x 3;

2x 1

x2 5x 6 2

2x,

x 3.

	Вариант 5
I.	Заштриховать ту	II.	Записать множество,
	часть диаграммы на		изображенное с
	рис. 9, которая		помощью кругов
	соответствует		Эйлера на рис. 10.
	множеству
	(A B) (C \ B).

Рис. 9	Рис. 10

III.Пользуясь определением равенства множеств, доказать, что

(A B) \ (A C) (A B) \ C .

IV. Пользуясь определением предела последовательности, доказать, что

lim	n3 2n	1	.
	1 3n3	3
n

V.Исследовать на сходимость последовательность с общим членом

a 1	2	3	n	.
	4	42	4n 1
n

VI. Пользуясь определением предела функции, доказать, что

а) lim	x2 2x 1	1	;	б) lim	x2	3x 2	.
	3x2 1	3			x2	4x 4
x				x 2

VII. Найти пределы, если они существуют.

en tg

(5 sin n)

;

а)

lim

;

б)

lim

arctg(n

1 7 sin

x2 tg 2 x

27x 3

г)

lim

;

д)

lim

;

1 2sin

x 1 3

x 0

		4x2 1			x2 5
в)	lim					;
		4x	2	1
	x
		sin2 3x
е)	lim					.

	x 0 1	cos 12x

VIII. Исследовать функции на непрерывность, установить характер точек разрыва:

2x x2 , 3 x 0;

а)

f x

0 x 2;

б) f (x)

x 1

5x 3

1 3x,

2 x 4.

	Вариант 6
I.	Заштриховать ту	II.	Записать множество,
	часть диаграммы на		изображенное с
	рис. 11, которая		помощью кругов
	соответствует		Эйлера на рис. 12.
	множеству
	(A \ B) (C \ B).

Рис. 11	Рис. 12

III.Пользуясь определением равенства множеств, доказать, что

(A B) \ C (A \ C) (B \ C) .

IV. Пользуясь определением предела последовательности, доказать, что

lim	3n2 n 2	.
	2n 3
n

V.Исследовать на сходимость последовательность с общим членом

an 4 2!4 3!4 n4! .

VI. Пользуясь определением предела функции, доказать, что

а) lim	3x2	x 7	1	;	б) lim	x2	3x 2	.
	9x2	4x 1	3			x2	4x 4
x					x 2

VII. Найти пределы, если они существуют.

4 en! tg

cos2

2 x 2

lim

а)

; б)

lim2

sin

;

в)

lim

;

arctg(n

4n 4)

x / 2

n 3n

1 tg 2x

cos 5x cos x ;

г)

lim

;

д)

lim

е)

lim x

2 x 2 .

arcsin

6 x2

x 0 sin 3x arctg x

x 0

1 arctg 4x

x 1

VIII. Исследовать функции на непрерывность, установить характер точек разрыва:

x 2,

3 x 1;

sin x 2

а) f (x)

, 1 x 3;

б) f x

x 10

x 3.

	Вариант 7
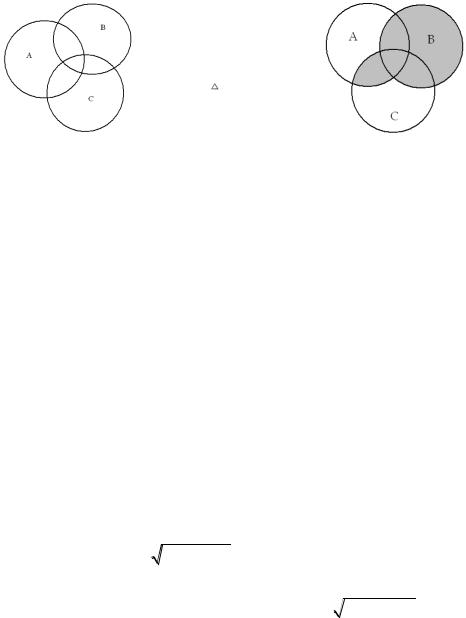
I.	Заштриховать ту	II.	Записать
	часть диаграммы на		множество,
	рис. 13, которая		изображенное с
	соответствует		помощью кругов
	множеству		Эйлера на рис. 14.
	(A C) (B \ C).
	Рис. 13		Рис. 2

III.Пользуясь определением равенства множеств, доказать, что

A \ (B \ C) (A \ B) (A C).

IV. Пользуясь определением предела последовательности, доказать, что

sin n

бесконечно малая при n .

последовательность

n n 1

V. Исследовать на сходимость последовательность с общим членом

1 n 1

VI. Пользуясь определением предела функции, доказать, что

а) lim

4x 3

0 ;

б)

lim

x 9

2x 4

9x 1

x 1

VII. Найти пределы, если они существуют.

а) lim

(7n2 9) sin(n4

cos 9n

; б)

lim

7 x2

2 x 14

;

в) lim

1 cos 4x

;

25n4

9n3

x 7

x2 49

x 0 arctg 9x2

sin 3x

arctg2 x

lim n 3

;

е) lim 1 2cos x tg x .

г) lim

;

д)

n3 4n2

2 cos x

x o

x 2

VIII. Исследовать функции на непрерывность, установить характер точек разрыва:

5x 1	, x 1;
	, x 1;		x 4
x 2			x 4
а) f x 3x 1, 1 x 2,		б) f x			.

			x	4


	x 2.
7,	x 2.

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2019249.15 Кб5математика экзамен.docx
#
22.02.20152.14 Mб13Математика.doc
#
22.02.20152.22 Mб14Математика.doc
#
23.02.20154.52 Mб40Математика.pdf
#
13.03.20164.55 Mб32Математика_2_2015.pdf
#
23.02.20151.16 Mб30Математический анализ ИДЗ №1 Введение в анализ.pdf
#
22.02.2015167.42 Кб13материал для реферата.doc
#
19.11.2019113.89 Кб3Материал для самост. изучения.docx
#
08.11.20192.2 Mб23Материал по вопросам.doc
#
10.11.2019385.02 Кб2Материализм XIX.doc
#
13.03.20162.14 Mб7материализм_и_эмпириокритицизм.pdf