
Часть 2 ВА и АГ интернет-материалы
.pdf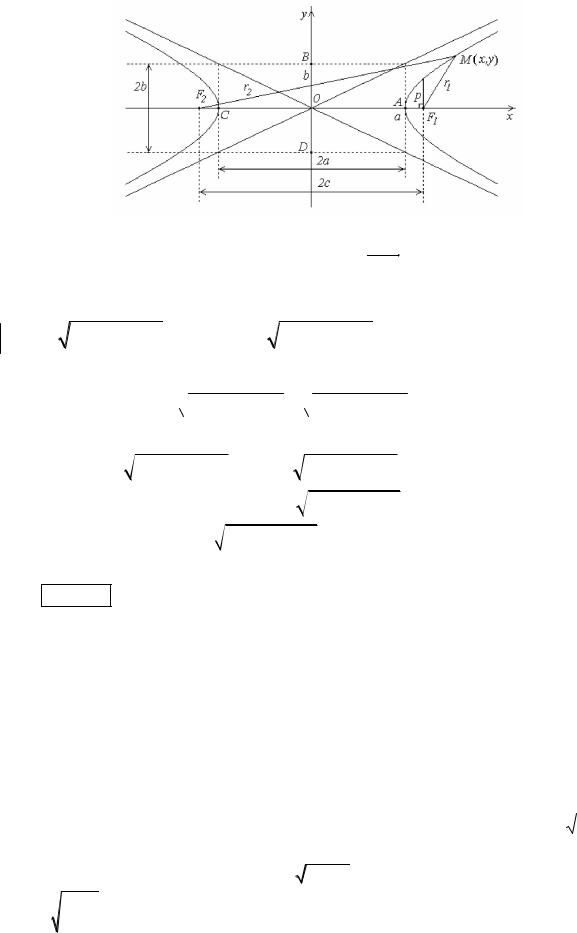
|
Вывод уравнения гиперболы. |
|
|
|
|
|
|||||||||
|
|
|
|
|
F1M |
|
|
|
|
2a и |
|
|
|
||
|
По определению |
|
|
F2 M |
|
F1 F2 |
2c, значит, а<с. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользуемся |
|
формулой |
|
расстояния |
между двумя точками |
|||||||||
|
|
|
|
|
|
|
|||||||||
F M |
(x c)2 y2 r , |
F M |
(x c)2 y2 r . |
||||||||||||
1 |
|
|
|
1 |
2 |
|
|
|
|
2 |
|
||||
По определению r1 r2 2a . Подставим в это равенство r1 и r2: 
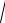 (x c)2 y2
(x c)2 y2 
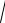 (x c)2 y2 2a.
(x c)2 y2 2a.
Проделаем преобразования:

 (x c)2 y2 2a
(x c)2 y2 2a 
 (x c)2 y2 ,
(x c)2 y2 ,
(x c)2 y2 4a2 4a
 (x c)2 y2 (x c)2 y2 , cx a2 a
(x c)2 y2 (x c)2 y2 , cx a2 a
 (x c)2 y2 ,
(x c)2 y2 ,
(c2 a2 )x2 a2 y2 a2 (c2 a2 ).
Если c2- a2=b2, то b2x2 - a2y2= a2b2 и
|
x2 |
|
y2 |
1 |
- каноническое уравнение гиперболы. |
|
a2 |
b2 |
|||
|
|
|
|
Гипербола – центральная линия второго порядка. Она состоит из двух бесконечных ветвей, симметрична относительно осей. Элементами гиперболы являются:
точка О - центр гиперболы; точки А и В - вершины гиперболы;
точки F1(+ с ,0) и F2(- с ,0) - фокусы гиперболы;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2с - фокусное расстояние, которое |
вычисляется по формуле |
c |
b2 a2 |
; |
||||||||||||
AB=2a - действительная ось гиперболы; |
|
|
|
|
||||||||||||
CD=2b - мнимая ось гиперболы, |
b |
|
|
; |
|
|
|
|||||||||
c2 a2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
c |
|
1 |
b2 |
|
, e 1 |
– эксцентриситет гиперболы. |
|
|
|
||||||
|
|
|
|
|
||||||||||||
|
a |
|
|
a2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
Эксцентриситет определяется отношением осей гиперболы и характеризует еe форму: чем больше e, тем более вытянут вдоль мнимой оси основной прямоугольник гиперболы.
Асимптоты гиперболы - это прямые, к которым ветви гиперболы неограниченно приближаются при удалении в бесконечность.
|
b |
|
|
||
Уравнения асимптот гиперболы имеют вид: |
y |
|
|
x |
. |
|
|||||
|
a |
|
|
||
Угол между асимптотами зависит от значения эксцентриситета гиперболы
e |
c |
1, он определяется из уравнения |
tg |
|
|
b |
. При |
a b гипербола |
|
|
|
||||||
|
a |
2 |
|
a |
|
|||
называется равнобочной, ее асимптоты взаимно перпендикулярны, уравнение гиперболы имеет вид: x2 y2 a2 . Если принять асимптоты за оси координат,
то уравнение гиперболы примет вид: xy a2 , то есть равнобочная гипербола
2
является графиком обратной пропорциональности.
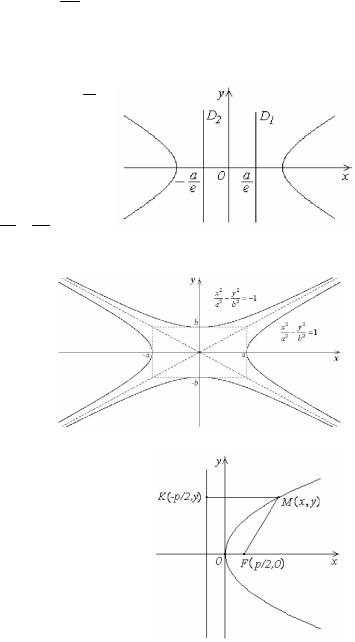
Прямые d1 и d2 , перпендикулярные действительной оси гиперболы и
отстоящие от ее центра на расстояниях d a , e
называются директрисами гиперболы, соответствующими фокусам F1 и F2. Отношение расстояния любой точки гиперболы до фокуса к расстоянию ее до соответствующей директрисы
постоянно и равно эксцентриситету r1 r2 e . d1 d2
Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях a и b определяются уравнениями:
|
x2 |
|
y2 |
1 |
и |
|
x2 |
|
y2 |
1 |
. |
|
a2 |
b2 |
|
a2 |
b2 |
||||||
|
|
|
|
|
|
|
|
Сопряженные гиперболы имеют общие асимптоты. Действительная ось одной из них есть мнимая ось другой .
Парабола
Параболой называется геометрическое место точек M(x,y), расстояние которых до определенной точки F(p/2,0) (называемой фокусом параболы) равно расстоянию до определенной прямой (называемой директрисой параболы).
33
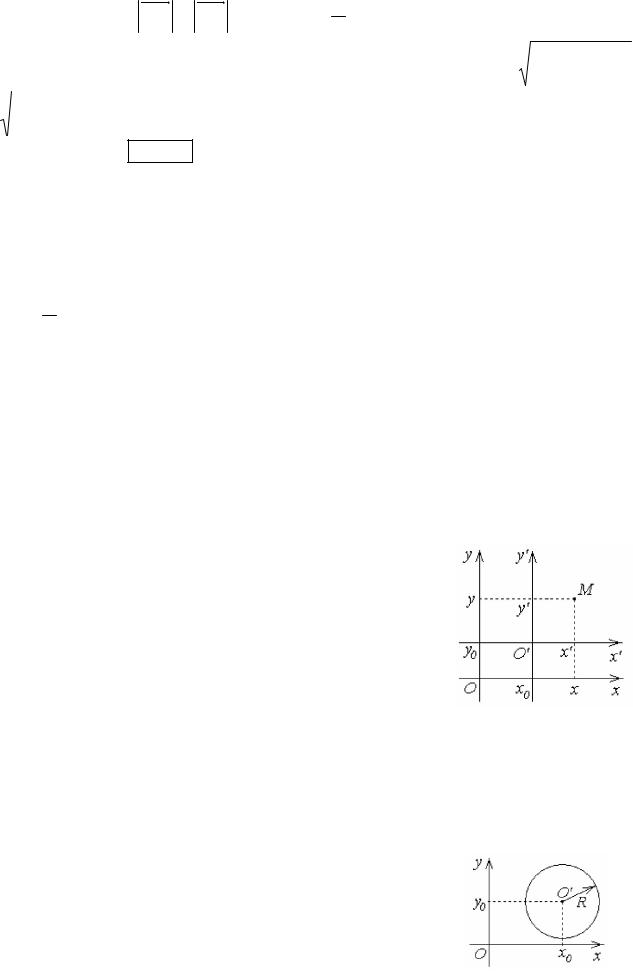
Вывод уравнения параболы.
По определению FM MK и r = d, d p x .
2
Воспользуемся формулой расстояния между двумя точками: r |
(x |
p |
)2 y2 , |
||||||||||
|
|||||||||||||
|
|
|
|
|
p |
|
p |
|
p |
|
2 |
|
|
|
(x |
p |
)2 y 2 |
|
x , (x |
)2 y2 ( |
x)2 . |
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
2 |
|
2 |
2 |
2 |
|
|
|
|
|||||
y2=2 p x - каноническое уравнение параболы.
Парабола – нецентральная линия второго порядка. Она состоит из одной бесконечной ветви, симметричной относительно оси. Элементами параболы являются:
точка О - вершина параболы; OX - ось параболы;
точка F(р/2,0) - фокус параболы;
x p - уравнение директрисы параболы;
2
e 1 - эксцентриситет параболы,
p - фокальный параметр (расстояние от фокуса до директрисы или половина длины хорды, проходящей через фокус перпендикулярно оси).
3.4.Преобразования координат Параллельный перенос
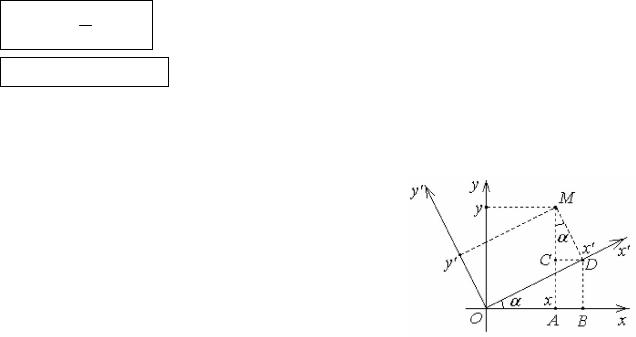
Перенесём начало координат из точки О в точку О1 параллельным переносом осей. Пусть в системе координат XOY точка М имеет координаты x и y. Система координат X O1Y получена из системы
координат XOY параллельным переносом осей, при котором начало координат О1 имеет координаты x0 и y0 в системе координат XOY.
Точка М в системе координат X O1Y имеет координаты x и y . Связь между координатами точки M(x,y) и точки M(x ,y ) в старой и новой системах координат задается формулами:
|
, |
|
|
, |
|
x x x0 |
(1) |
x x x0 |
|||
|
|
, |
|
(2) |
|
y y y0 |
|
y y y0. |
|||
Уравнения кривых второго порядка, когда их центры симметрии находятся в точке с координатами O1(x0,y0), получаются с помощью преобразования координат при параллельном переносе осей (2):
(x x |
)2 ( y y )2 |
R2 |
- уравнение окружности с |
0 |
0 |
|
|
центром в точке O1(x0,y0) и радиусом R;
34
|
(x x )2 |
|
(y y |
)2 |
1 |
- уравнения эллипса и гиперболы с центром симметрии |
|
0 |
0 |
|
|||
|
a2 |
b2 |
|
|||
|
|
|
|
|
в точке O1(x0,y0);
y y0 b (x x0 ) - уравнения асимптот гиперболы; a
(y y0 )2 2 p(x x0 ) - уравнение параболы с вершиной в точке O1(x0,y0).
Поворот координатных осей
Выведем формулу преобразования координат при повороте координатных осей.
Повернём оси координат на угол относительно исходной системы координат. Координаты точки М в системе координат
|
|
равны x и y . Найдём её координаты в |
||
X O Y |
|
|||
системе координат XOY . В треугольнике CMD |
||||
CMD , OD x , MD y . |
|
|
||
Следовательно, x=OA=OB-AB=OB-CD, y=MA=AC+CM=DB+CM. |
||||
Поскольку |
|
|
||
|
|
|
|
|
|
|
OB x |
cos , CD y sin , |
|
|
|
|
|
|
|
|
CM y |
cos , DB x sin , |
|
то |
|
x x cos y sin , |
||
|
|
|
(3) |
|
|
|
y x sin y cos . |
||
Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x ,y ) этой же точки при повороте осей на угол .
Формулы, выражающие новые координаты (x ,y ) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система получена поворотом старой на угол , то старая система получается поворотом новой на угол (- ), поэтому в равенствах (3) можно поменять местами старые и новые координаты, заменяя одновременно на (- ).
Выполнив это преобразование, получим
x xcos ysin ,
y xsin y cos .
Изменение начала координат и поворот осей
Если оси декартовой прямоугольной системы переносятся параллельно на величины x0 по оси ox и на y0 по оси oy и, кроме того, поворачиваются на угол
35
, то этому изменению системы соответствуют формулы преобразования координат, выражающие старые координаты через новые
x x cos y sin x0 ,
y x sin y cos y0 ,
и новые координаты через старые:
|
|
|
|
)sin , |
||
x |
(x x )cos ( y y |
|||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
)cos . |
y (x x )sin ( y y |
||||||
|
|
|
|
0 |
0 |
|
Приведение общего уравнения кривой второго порядка к каноническому виду
Пусть кривая второго порядка задана в общем виде:
Ax2 2Bxy Cy2 2Dx 2Ey F 0 .
(4)
(5)
(6)
Всякая линия второго порядка есть либо эллипс, либо парабола, либо гипербола, либо распадается на пару прямых (пересекающихся, параллельных или совпадающих).
Приведение этого уравнения к каноническому виду заключается в
нахождении системы координат, в которой кривая имеет канонический вид, геометрически это может быть достигнуто поворотом координатных осей на угол, совмещающий оси симметрии кривой с координатными осями и переносом начала координат в центр или вершину кривой x0 , y0 . Кривые
второго порядка, имеющие центр, называются центральными.
Алгебраически это приводит к сокращению членов с произведением текущих координат и членов, содержащих их в первой степени, после применения формул (1) и (3).
1). Преобразуем уравнение (6) поворотом осей координат на угол так, чтобы исчезло слагаемое, содержащее произведение неизвестных. Преобразование поворота имеет вид:
x x cos y sin , y x sin y cos ,
где x , y - новые координаты. Уравнение примет вид:
A1x 2 2B1x y C1 y 2 2D1x 2E1 y F1 0 ,
где главный интерес представляет коэффициент перед произведение x y :
B1 2Asin cos 2B(cos2 sin2 )
.
2C sin cos 2Bcos 2 (C A)sin 2 .
Найдём угол поворота из условия B1 0 : 2B cos 2 ( A C) sin 2 , откуда
36

|
|
|
|
|
А С, |
||
|
|
|
|
, |
|
|
|
4 |
|
|
|||||
|
|
2B |
(7) |
||||
1 |
|
|
|||||
|
|
arctg |
А С. |
||||
|
|
|
|
|
, |
||
2 |
|
|
|||||
|
|
|
A C |
|
|||
Каноническое уравнение кривой принимает вид:
A1 x 2 C1 y 2 2D1 x 2E1 y F1 0,
где |
A B sin 2 |
1 |
A C cos 2 |
1 |
A C |
, |
|
||||
|
|
|
|||||||||
1 |
2 |
|
|
2 |
|
|
|
|
|||
|
|
|
1 |
|
1 |
|
|
|
|||
|
C B sin 2 |
A C cos 2 |
A C |
. |
|||||||
|
|
|
|||||||||
|
1 |
|
2 |
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|||
2). Члены, содержащие переменные в первой степени, исчезают после выделения в общем уравнении полных квадратов, тем самым алгебраически позволяют найти центр или вершину кривой после применения формул
x x x0 ,
y y y0 .
Заметим, что преобразование параллельного переноса не изменяет коэффициентов A1 и C1 и конечный результат преобразований может быть проанализирован уже после преобразования поворота. Кроме того, при преобразовании поворота коэффициенты уравнения меняются,
|
Ax2 2Bxy Cy2 |
2Dx 2Ey F 0 |
||||||||
переходит в |
A1 x 2 C1 y 2 2D1 x 2E1 y F1 0, |
|||||||||
|
||||||||||
но некоторые комбинации коэффициентов, а именно, |
||||||||||
I1 A1 C1 |
A C и I2 |
|
A1 |
B1 |
|
A1C1 |
|
A B |
|
AC B2 |
|
|
|
|
|||||||
|
|
|
B1 |
C1 |
|
|
|
B C |
|
|
сохраняют свои значения. Такие величины носят название инвариантов (неизменных величин) уравнения второй степени.
С помощью инвариантов различают три типа линий второго порядка. 1). Эллиптический тип, если I2 AC B2 0 .
К этому типу относятся, кроме действительного эллипса, также мнимый эллипс
x2 y2 1 a2 b2
и пара мнимых прямых, пересекающихся в действительной точке
x2 |
|
y2 |
|||
|
|
|
|
|
0. |
a |
2 |
b |
2 |
||
|
|
|
|
||
2). Гиперболический тип, если I2 AC B2 0 .
К нему относится, кроме гиперболы, пара действительных пересекающихся прямых
37
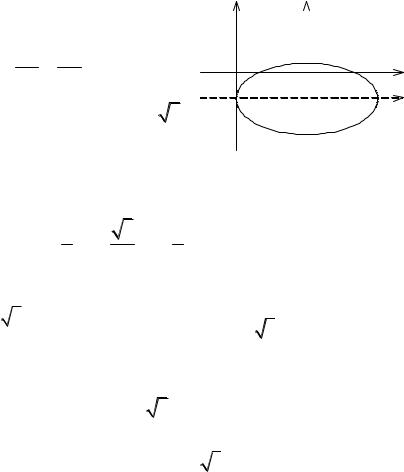
x |
2 |
|
y2 |
||
|
|
|
|
|
0 . |
a |
2 |
b |
2 |
||
|
|
|
|
||
3). Параболический тип, если I2 AC B2 0 .
К нему относится, кроме параболы, пара параллельных (действительных или мнимых) прямых (они могут совпадать).
ПРИМЕР: Приведите уравнение 5x2 9y2 30x 18y 9 0 к каноническому виду и постройте кривую.
Выделим полный квадрат: сгруппируем члены этого уравнения, содержащие одноименные координаты:
5x2 30x 9y2 18y 9 0 , |
5 x2 6x 9 y2 2y 9 0 . |
Дополним члены в скобках до полных квадратов:
5 x2 6x 9 9 9 y2 2y 1 1 9 0, 5 x 3 2 9 y 1 2 45.
Введем новые координаты: x x 3, y y 1, x0 |
3, |
y0 1, |
|
||||||||||||
то есть точка O1 3, 1 |
– центр кривой. |
|
|
|
|
|
|||||||||
Уравнение в новой системе координат |
y |
|
y |
|
|||||||||||
принимает вид: |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
y |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
45 |
|
|
|
|
1, |
|
|
|
|
x |
|
5x 9y |
|
|
|
|
|
|
|
0 |
|
|
|||||
|
|
|
|
|
|
9 |
5 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
01 |
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
определяет эллипс |
|
с |
|
полуосями |
|
a 3, |
b 5, |
|
|
|
|
||||
который в исходной системе координат имеет |
|
|
|
|
|||||||||||
центр в точке O1 3, 1 . |
|
|
|
|
|
|
|
|
|
|
|||||
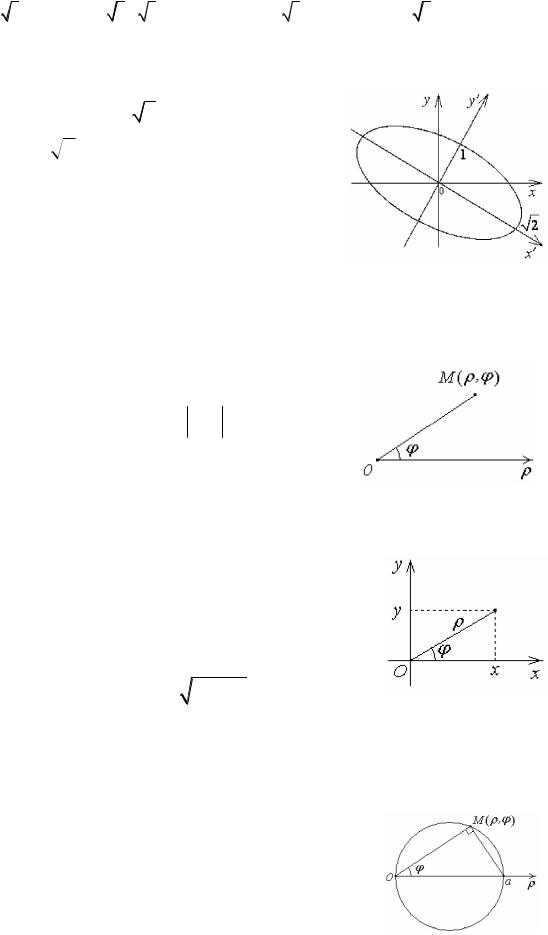
ПРИМЕР: Определите вид кривой 5 x2 |
3 xy 7 y2 |
2. |
|
|
|
||||||||||
4 2 4
Определим угол поворота осей по формуле (7):
A |
5 |
,C |
7 |
,B |
3 |
, |
|
1 |
arctg |
2B |
|
1 |
arctg |
|
|
|
. |
|
3 |
||||||||||||||||||
|
|
4 |
|
A C |
|
|
||||||||||||
4 |
4 |
|
|
2 |
2 |
6 |
|
|||||||||||
Подвергнем уравнение кривой преобразованию:
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|||
|
sin |
|
|
|
|
|
|
|
|||||||
x x |
cos y |
2 |
|
x |
2 |
|
y , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
y x sin y cos |
|
|
|
x |
|
|
|
|
|
y |
|||||
2 |
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
и получим уравнение эллипса
38
5 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
7 |
|
1 |
|
|
|
|
|
2 |
|
|||||||||||||
3 |
|
|
3 |
|
|
3 |
|
|
|
|
3 |
|
|
3 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|||||||||
4 |
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
4 |
|
|
2 |
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
x |
2 |
2y |
2 |
2 |
|
|
|
|
|
x |
2 |
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
, |
|
|
|
|
|
|
2 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
с полуосями a 
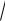 2 , b 1.
2 , b 1.
3.5. Линии в полярной системе координат
Полярные координаты определяются заданием на плоскости полюса О (0,0) и полярной оси .
Координаты точки М в полярных координатах
задаются длиной радиус-вектора OM этой точки
и углом его наклона к полярной оси, отсчитываемым против часовой стрелки.
При этом 0 , 0 2 .
Связь полярных координат с декартовыми
Совместим начало декартовой системы с полюсом полярной системы координат, а ось OX с полярной осью .
Связь координат точки M(x,y) и M( , ):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x cos , |
|
|
x2 y2 , |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y sin , |
|
arctg |
. |
|
|
|
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||
Окружности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим линию a cos , а=const >0. |
|
|
|||||||||||||
1). По точкам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
|
0 |
30 |
|
45 |
|
|
60 |
90 |
|
|||||
|
|
|
а |
0,86 а |
|
0,7 а |
|
|
0,5 а |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 , с возрастанием угла |
от 0 до |
/2 косинус этого |
||||||||||||||
39
угла убывает от 1 до 0, таким образом, убывает от а до 0 в точке О(0, /2), и радиус-вектор точки М описывает верхнюю половину окружности. Нижняя её половина получается при изменении от 3 /2 до 2 . Этим значениям угла соответствуют положительные значения cos , возрастающие от 0 до 1, что приводит к возрастанию от 0 до а и геометрическому замыканию окружности.
Уравнение a cos задаёт окружность с центром в точке (a/2,0) и радиусом a/2.
2). В уравнении линии a cos перейдем к декартовым координатам:
|
|
|
x |
, x2 y2 ax 0, (x |
a |
)2 y2 |
a2 |
|
x2 y2 a |
|
, |
||||||
|
|
|
|
|||||
|
|
|
x2 y2 |
2 |
4 |
|
||
каноническое уравнение окружности с центром в точке (a/2,0) и радиусом a/2. Постройте самостоятельно кривую asin , a > 0.
Спирали
Архимедова спираль: = а ,0 , 0 .
Для построения архимедовой спирали нужно вычислить значения при различных значения :
OA a ;OB 2OA 2 a ;OC 3OA 3 a ; и так далее.
2 2 2
Кривая представляет собой линию, описываемую точкой, движущейся с постоянной скоростью по лучу, вращающемуся около полюса О с постоянной
скоростью : a v .
Гиперболическая спираль: a , a > 0,0 , 0 .
40
Логарифмическая спираль:
a , a 1; - , 0 . |
a , 0< a 1; - , 0 |
||||||||||||||||
Розы |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
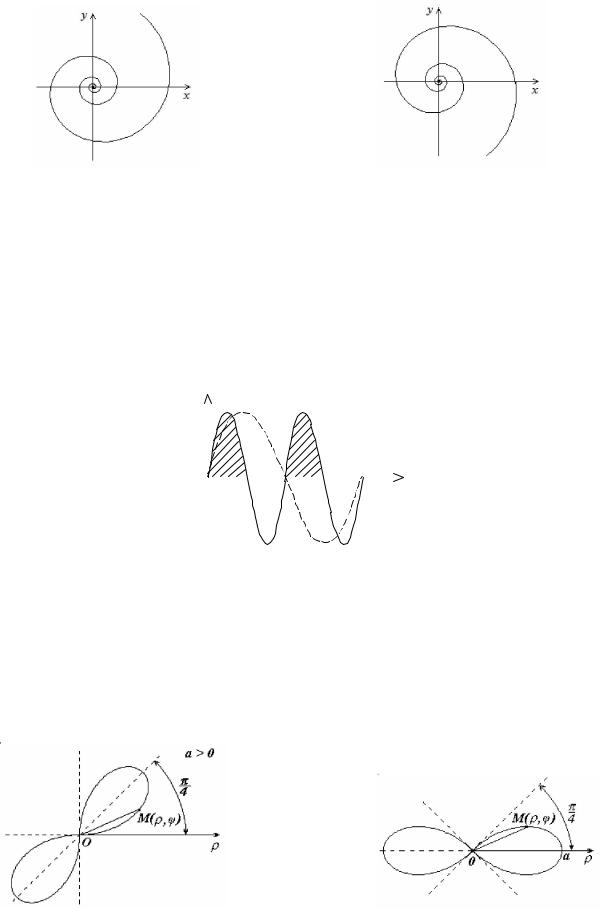
Двухлепестковые розы: asin 2 , a>0; 0 2 , 0 a . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
0 |
30 |
45 |
60 |
|
90 |
|
|||||||||
|
|
0 |
0,7 а |
|
|
а |
0,7 а |
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
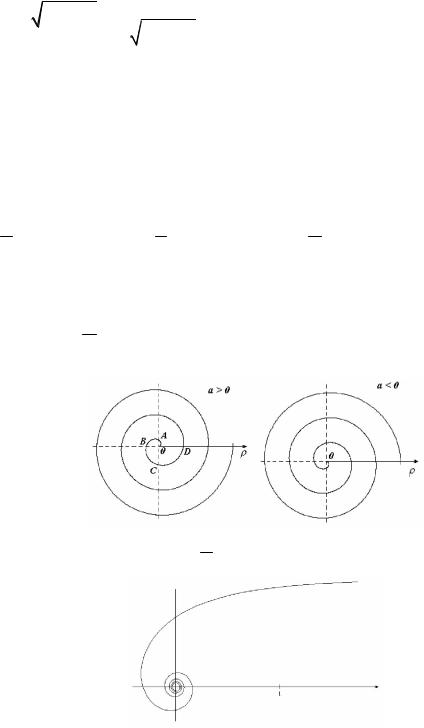
График функции asin 2 для [0,2 ) : |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
= sin |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
/2 |
|
|
3 /2 |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
/4 |
|
5 /4 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция |
asin 2 при а>0 принимает допустимые, неотрицательные |
||||||||||||||||||||||||
значения 0 |
при |
[0, |
|
] [ , |
3 |
]; |
принимает |
максимальные, равные а, |
|||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
значения при |
|
|
и |
|
5 |
, |
интервалами возрастания функции являются |
||||||||||||||||||
|
|
||||||||||||||||||||||||
|
1 |
4 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
3 |
|||||||||||
значения [0, |
) [ , |
) , убывания |
, |
, |
|||||||||||||||||||||
|
|
– |
|
|
|
|
|
|
. Аналогично |
||||||||||||||||
|
|
|
2 |
|
2 |
||||||||||||||||||||
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|||||||
строим кривую, содержащую косинус.
asin 2 , a>0; 0 2 , 0 a ; |
a cos2 , a>0; |
0 2 , |
0 a |
41
