
Часть 2 ВА и АГ интернет-материалы
.pdf
|
|
|
|
|
|
|
Угол между двумя прямыми |
|
|||||||||||||||||
Если a1 {l1,m1, n1} |
|
и a2 |
{l2 , m2 ,n2} направляющие век- |
|
|||||||||||||||||||||
торы прямых L1 и L2 , то абсолютная величина косинуса уг- |
|
||||||||||||||||||||||||
ла между этими векторами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
l1l2 m1m2 n1n2 |
|
|
|
|
L1 |
L2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
l2 |
m2 |
n2 |
|
l2 |
m2 n2 |
|
|||||||||||||||||||
|
|
|
|
1 |
|
1 |
1 |
2 |
|
2 |
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
дает угол между прямыми |
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
Условие параллельности и перпендикулярности двух прямых |
|||||||||||||||||||||||||
Прямые будут параллельны, если их направляющие векторы a1 и a2 |
|||||||||||||||||||||||||
параллельны, то есть |
|
|
l1 |
|
|
m1 |
|
n1 |
. |
|
|
|
|
|
|||||||||||
|
l2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
m2 |
|
|
n2 |
|
|
|
|
|
|
|
|
||||||||
Прямые будут перпендикулярны, если их направляющие векторы пер- |
|||||||||||||||||||||||||
пендикулярны, то есть |
|
|
|
|
l1l2 |
m1m2 |
n1n2 |
0 |
. |
|
|||||||||||||||
ПРИМЕР: Определите угол между двумя прямыми:
3x 4y 2z 0, |
4x y 6z 2 0, |
||
|
2x y 2z 0, |
|
y 3z 2 0. |
|
|
||
Находим направляющие векторы данных прямых. Нормальные векторы плоскостей, задающих первую прямую, n1 {3, 4, 2}, n2 {2,1, 2}, и вторую прямую, Направляющие векторы первой и второй прямых:
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
i |
j |
|
|
|
|
|
||||||||||
|
|
3 |
|
4 |
|
2 |
|
|||||||||||||||
a1 |
n1 |
n2 |
|
|
10i 2 j 11k , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
|
|
|
|
|
||||||||||
|
|
4 |
1 6 |
|
||||||||||||||||||
a2 n3 |
n4 |
3i 12 j 4k , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
1 |
|
3 |
|
|
|
|
|
|
|
|
||
cos |
|
|
|
|
|
10 3 2 12 11 4 |
|
|
|
|
98 |
; |
||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
102 22 112 |
|
|
32 122 |
42 |
195 |
|
|||||||||||||
arccos 98 .
195
22
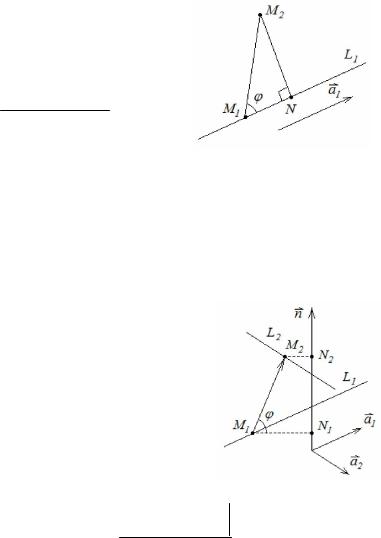
Расстояние от точки до прямой
Пусть прямая L1 с направляющим вектором a1 {l1, m1, n1} проходит че-
рез точку M1(x1, y1, z1). Найдем расстояние от точки M2 (x2 , y2 , z2 ) до прямой, для чего построим вектор
M1M2 {x2 x1, y2 y1, z2 z1}.
Длина перпендикуляра M2 N , опущенного из точки
M2 на прямую L1 (она же – искомое расстояние):
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
M |
a |
|
|
||||
|
|
|
|
1 |
2 |
1 |
|
|
|
||
M2 N d |
M1M2 |
sin |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Расстояние между двумя прямыми
Пусть прямая L1 с направляющим вектором a1 {l1, m1, n1} проходит через
точку M1(x1, y1, z1), а прямая L2 с направляющим вектором a2 {l2 , m2 , n2} – через точку M2 (x2 , y2 , z2 ) .
Построим вектор M1M2 {x2 x1, y2 y1, z2 z1} и спроектируем его на направление n нормали к векторам
a1 и a2 . Длина проекции N1N2 и будет искомым расстоя-
нием. Нормаль может быть задана как n a1 a2 , а мо-
дуль проекции N1N2 может рассматриваться как высота параллелепипеда, построенного на векторах M1M2 , a1 ,
a2 как на ребрах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
V |
|
M1M |
2 |
a1 |
a2 |
||||
|
|
|||||||||||
N1N2 d |
M1M2 |
sin |
параллелепипеда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||
|
|
|
Sоснования |
|
|
a1 |
a2 |
|
|
|||
|
|
|
||||||||||
Если прямые параллельны, то ищем расстояние от точки M2 до прямой
L1 (как в предыдущем параграфе).
2.4. Прямая и плоскость
Точка пересечения прямой и плоскости
Пусть известны уравнения прямой и плоскости:
L : |
x x0 |
|
y y0 |
|
z z0 |
; |
P : Ax By Cz D 0 . |
l |
m |
|
|||||
|
|
|
n |
|
|||
Координаты точки пересечения прямой и плоскости должны одновременно удовлетворять этим уравнениям.
23

1). Выражая две переменные через третью из уравнений прямой и подставляя их в уравнение плоскости, получим уравнение для одной переменной и найдем точку пересечения прямой и плоскости.
2). Можно перейти к параметрическим уравнениям прямой:
|
|
x x0 lt, |
y y0 mt, z z0 nt , |
|||
тогда подстановка переменных в уравнение плоскости P позволяет найти зна- |
||||||
чение параметра |
t0 |
|
Ax0 By0 |
Cz0 D |
для координат точки пересечения |
|
Al Bm Cn |
||||||
|
|
|
|
|||
прямой и плоскости.
3). Если прямая задана общими уравнениями, точка пересечения может быть найдена как решение системы из трех уравнений плоскостей.
Уравнение пучка плоскостей, проходящих через прямую
Пусть прямая задана линией пересечения двух плоскостей:
A1 x B1 y C1 z D1 0,A2 x B2 y C2 z D2 0.
Возьмем любые отличные от нуля числа и и составим равенство
( A1 x B1 y C1 z D1 ) ( A2 x B 2 y C 2 z D 2 ) 0 .
Это равенство определяет произвольную плоскость, проходящую через ту же прямую.
Совокупность всех плоскостей, проходящих через одну и ту же прямую, назы-
вается пучком плоскостей. Если положить 0 и , то уравнение
A1 x B1 y C1 z D1 (A2 x B2 y C2 z D2 ) 0
определяет все плоскости пучка, кроме второй из плоскостей, задающих прямую.
24
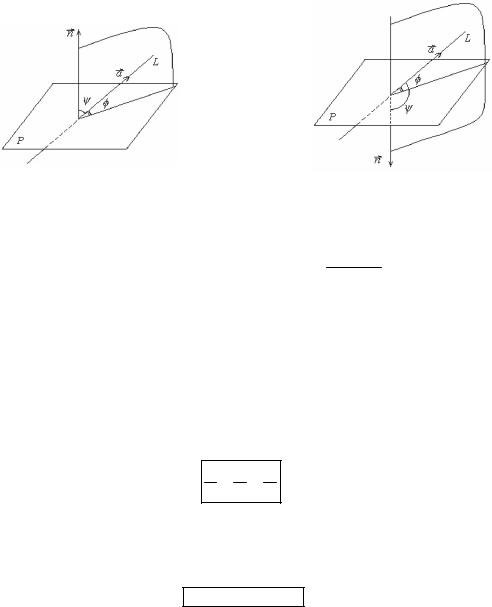
Угол между прямой и плоскостью
Угол между прямой и плоскостью определяется как угол между пря-
мой и ее проекцией на плоскость. Пусть – угол между вектором нормали n к
плоскости и направляющим вектором |
a |
прямой. Если угол острый, то |
|||||||
|
|
|
|
|
|
|
|
||
|
, если угол тупой, то |
, т. е. |
|
|
. |
||||
|
|
2 |
|||||||
2 |
|
2 |
|
|
|
||||
|
|
sin sin |
|
|
|
|
cos |
|
|
|
n a |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
n |
|
a |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
Условия параллельности и перпендикулярности |
|||||||||||||||||||||||||
прямой L : |
x x0 |
|
y y0 |
|
z z0 |
и плоскости |
|
P : Ax By Cz D 0 |
|||||||||||||||||
l |
|
|
|
||||||||||||||||||||||
|
|
m |
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||
Прямая L перпендикулярна плоскости P, если направляющий вектор прямой коллинеарен нормальному вектору плоскости, то есть
A B C . l m n
Прямая L параллельна плоскости P, если направляющий вектор прямой перпендикулярен нормальному вектору плоскости, (a n) 0, то есть
Al Bm Cn 0.
25
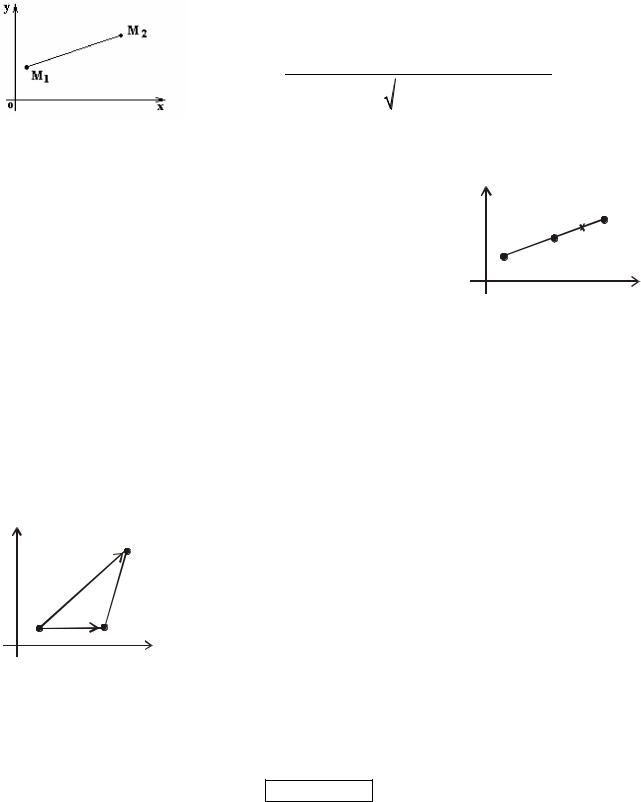
3.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
3.1.Простейшие задачи на плоскости
Расстояние между двумя точками
|
|
|
|
|
|
Даны две точки M1(x1,y1) и M2(x2,y2). Расстояние между |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ними равно длине вектора |
M1M2 x2 |
x1 ,y2 y1 и |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
может быть вычислено по формуле |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
x x 2 |
y y 2 |
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M M |
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
1 |
|
2 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Деление отрезка в данном отношении |
|
|
|
|
|
||||||||||||||||||||||||||||
|
Точка M(x,y) делит отрезок M1M2 |
|
в отношении , |
y |
|
|
|
|
|
|||||||||||||||||||||||||||||
если |
x x1 |
|
y y1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
x2 x |
y2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|||
|
Координаты |
точки |
М находятся по |
|
формулам: |
|
|
|
|
|
C |
|||||||||||||||||||||||||||
|
|
|
M1 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
1 |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y1 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Координаты середины отрезка С получаются при М1М = ММ2, =1: |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x |
x1 x2 |
, y |
y1 y2 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
2 |
|
|
c |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Площадь треугольника |
|
|
|
|
|
|
|
|||||||||||||||||||||||
y |
|
M3 |
Пусть треугольник задан координатами своих вершин: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М1(x1,y1), M2(x2,y2), M3(x3,y3). |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x1 |
|
y1 |
|
1 |
|
|
|
|
|
|
1 |
|
x2 x1 |
y2 y1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
S |
|
|
x |
|
y |
2 |
|
1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x3 x1 |
y3 y1 |
|
|
|
|||||
M1 |
M2 |
|
|
|
|
|
|
|
|
|
x3 |
|
y3 |
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.2. Прямая линия на плоскости
Уравнения прямой
Общее уравнение прямой на плоскости XOY можно получить из общего уравнения плоскости в пространстве при z= 0:
Ax+By+C = 0.
Если А= 0 (В= 0), то прямая параллельна оси OX (оси OY). Если С= 0, то прямая проходит через начало координат.
26
Если прямая проходит через точку (x0,y0) перпендикулярно вектору n A, B , ее уравнение принимает вид: A(x x0 ) B(y y0 ) 0 .
Каноническое уравнение прямой
Если прямая проходит через точку (x0,y0) параллельно направляющему вектору a l,m , то получаем каноническое и параметрические уравнения
прямой на плоскости в виде:
|
|
|
|
|
|
|
|
x x0 lt, |
|
|
x x |
0 |
|
y y |
0 |
|
и |
||
|
|
|
|
|
|
||||
|
l |
|
m |
|
|
||||
|
|
|
|
|
|
y y0 |
mt, |
||
|
|
|
|
|
|
|
|
|
|
где t - параметр, t ( , ) .
Уравнение прямой, проходящей через две точки
Пусть на плоскости заданы две точки M1(x1,y1), M2(x2,y2). Уравнение прямой, проходящей через эти точки, можно записать как условие коллинеарности векторов
M1M2 č MM1 , где M(x,y) – произвольная точка прямой. Искомое уравнение получаем в виде
|
x x1 |
|
y y1 |
|
. |
|
x2 x1 |
y2 y1 |
|||
|
|
|
|||
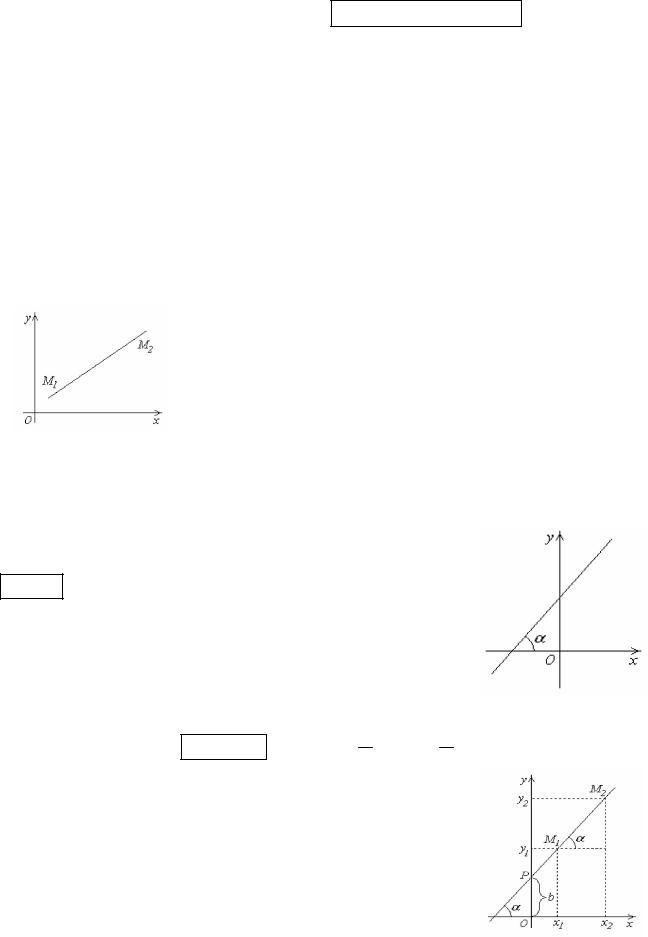
Уравнение прямой, проходящей через данную точку
в заданном направлении
Пусть прямая составляет угол с осью ох. Угловым коэффициентом прямой k называется число
k tg .
Прямая может быть задана точкой М1(x1,y1) и угловым коэффициентом k или двумя точками М1(x1,y1) и М2(x2,y2).
Уравнение прямой с угловым коэффициентом k
может быть получено из общего уравнения прямой
Ax+By+C=0, если B 0 :
y k x b , где k А и b C . B B
Прямая пересекает ось oy в точке P(0,b).
Из уравнения прямой, проходящей через две точки, имеем
y y |
y2 y1 |
(x x ) , |
y2 y1 |
tg k , |
|
|
|||||
|
|
|
|||
1 |
x2 |
x1 |
1 |
x2 x1 |
|
|
|
||||
y y1 k(x x1).
27
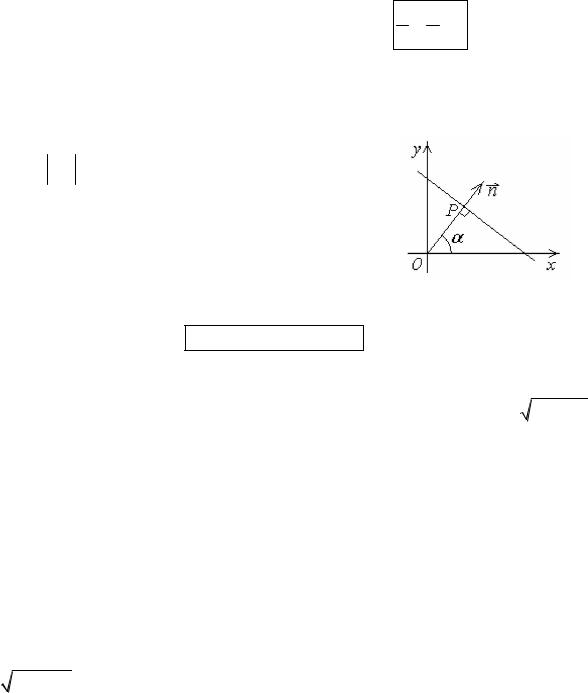
Уравнение прямой в отрезках
Общее уравнение прямой Ax+By+C=0 при C 0 может быть
преобразовано к виду уравнения прямой “в отрезках”: x y 1 . a b
Прямая в отрезках пересекает ось Оx в точке А(а,0) и ось Оy в точке
В(0,b).
Нормальное уравнение прямой
Пусть известно расстояние от прямой до начала координат OP p и угол между перпендикуляром
к прямой и положительным направлением оси OX. Из нормального уравнения плоскости в
пространстве, полагая z= 0 и учитывая, что
|
|
|
||
cos |
|
|
sin , |
|
2 |
||||
|
|
|
||
получаем нормальное уравнение прямой на плоскости в виде
xcos ysin p 0 .
Нормальное уравнение прямой можно получить из общего уравнения
1
прямой Ax+By+C= 0, умножив его на нормирующий множитель  .
.
 A2 B2
A2 B2
Знак числа должен быть противоположен знаку числа С.
Косинусы углов, образуемых прямой с осями координат, называются
направляющими косинусами прямой.
Если угол между прямой и осью OX равен и угол между прямой и осью OY равен , то cos2 cos2 1.
Расстояние от точки до прямой
Расстояние d от точки M0(x0,y0) до прямой, задаваемой нормальным уравнением, равно модулю отклонения точки от прямой , d = | |:
d |
|
Ax By C |
. |
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|||
 A2 B2
A2 B2
По этой формуле положительно, если точка М0 и начало координат лежат по разные стороны от прямой, в противном случае отрицательно.
Координаты точки пересечения двух прямых
Если прямые заданы уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, то координаты точки их пересечения (x0, y0) получаются как решение системы уравнений
A1x B1 y C1 0,
A2 x B2 y C2 0
28
|
|
|
|
B1 |
C1 |
|
|
|
|
|
|
|
C1 |
A1 |
|
|
|
|
|
|
по формулам Крамера в виде x |
|
|
|
B2 |
C2 |
|
|
, y |
0 |
|
|
|
C2 |
A2 |
|
|
, при |
A1 |
B1 |
0. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
A1 |
B1 |
|
|
|
|
|
|
A1 |
B1 |
|
|
|
A2 |
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
А2 |
B2 |
|
|
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|
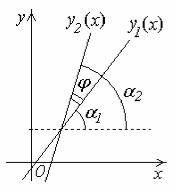
Угол между двумя прямыми
Пусть две прямые заданы уравнениями: y1 k1x b1,
y2 k2 x b2.
Острый угол пересечения этих прямых (отсчитываемый по часовой стрелке) находится из следующих соотношений:
tg |
|
tg( 2 1 ) |
|
|
|
tg 2 tg 1 |
|
|
|
k2 k1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|||||||||
|
|
1 tg 1 tg 2 |
1 k2 k1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие параллельности и перпендикулярности двух прямых
Если прямые заданы уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, то они
параллельны, если |
A1 |
|
B1 |
, и перпендикулярны, если |
A A B B 0 . |
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||
|
A2 |
|
B2 |
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Прямые y1=k1x+b1 и y2=k2x+b2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
параллельны друг другу, если 0 , tg 0: |
k1=k2 |
; |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
перпендикулярны друг другу, если |
, tg : |
k |
k |
|
1 |
|
k |
1 |
|
. |
|||||||||
|
2 |
|
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
1 |
k2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.3. Кривые второго порядка
Кривые второго порядка на плоскости определяются алгебраическими уравнениями второго порядка.
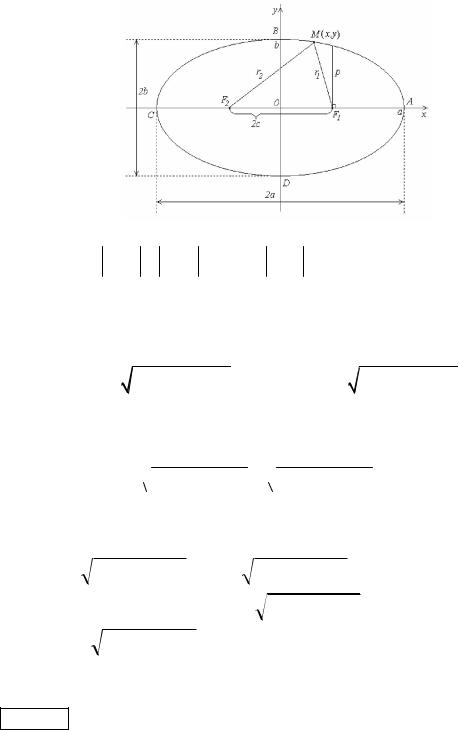
Эллипс
Эллипсом называется геометрическое место точек M(x,y), для которых сумма расстояний до двух заданных точек F1(+с,0) и F2(-с,0) (называемых фокусами эллипса) постоянна и равна 2а.
29
Вывод уравнения эллипса.
По определению F1M F2M 2a и F1F2 2c . Рассмотрим случай a c , так
как при a c получается отрезок F1F2 .
Воспользуемся формулой расстояния между двумя точками:
|
|
|
|
|
|
|
|
|
|
|
|
|
F M |
(x c)2 |
y2 r , |
F M |
(x c)2 |
y2 |
r . |
||||
|
1 |
|
|
1 |
2 |
|
|
|
|
2 |
|
По определению r1 r2 |
2a . Подставим в это равенство r1 |
и r2: |
|||||||||

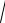 (x c)2 y2
(x c)2 y2 
 (x c)2 y2 2a .
(x c)2 y2 2a .
Проделаем преобразования:

 (x c)2 y2 2a
(x c)2 y2 2a 
 (x c)2 y2 ;
(x c)2 y2 ;
(x c)2 y2 4a2 4a
 (x c)2 y2 (x c)2 y2 ; a
(x c)2 y2 (x c)2 y2 ; a
 (x c)2 y2 a2 cx;
(x c)2 y2 a2 cx;
(a2 c2 )x2 a2 y2 a2 (a2 c2 ).
Если a2- c2=b2, то b2x2+a2y2=a2b2 и
|
x2 |
|
y2 |
1 |
- каноническое уравнение эллипса. |
|
a2 |
b2 |
|||
|
|
|
|
Убедиться, что любая точка, координаты которой удовлетворяют этому уравнению, принадлежит эллипсу, можно следующим образом. Из каноничес-
кого уравнения получим, что y |
2 |
b |
2 |
|
x2 |
|
|
|
|||
|
|
1 |
|
. Подставим это выражение в |
|||||||
|
|
a2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
соотношение |
F1M |
|
F2M |
2a , |
|
взятое |
в |
виде |
|||
|
|
|
|
|
|
30 |
|
|
|
|
|
(x c)2 y2 |
|
(x c)2 y2 |
2a . После преобразований получим верное |
равенство. |
|
|
|
Эллипс – центральная линия второго порядка, замкнутая линия, симметричная относительно осей и центра. Элементами эллипса являются: точка О - центр эллипса;
точки A, B, C, D - вершины эллипса; точки F1(с,0), F2(-с,0) - фокусы эллипса;
2c - фокусное расстояние, которое вычисляется по формуле c 
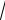 a2 b2 ;
a2 b2 ;
АВ=2а и CD=2b - большая и малая оси эллипса; a и b - большая и малая полуоси эллипса;
e c , (e 1) - эксцентриситет эллипса, который вычисляется по формуле
|
a |
|
|
|
||
e |
1 |
b2 |
|
|
. |
|
a2 |
|
|||||
|
|
|
|
|
|
|
Эксцентриситет определяется отношением осей эллипса и характеризует
его форму: чем больше e, тем более вытянут эллипс вдоль большой оси. |
|
|||||||||
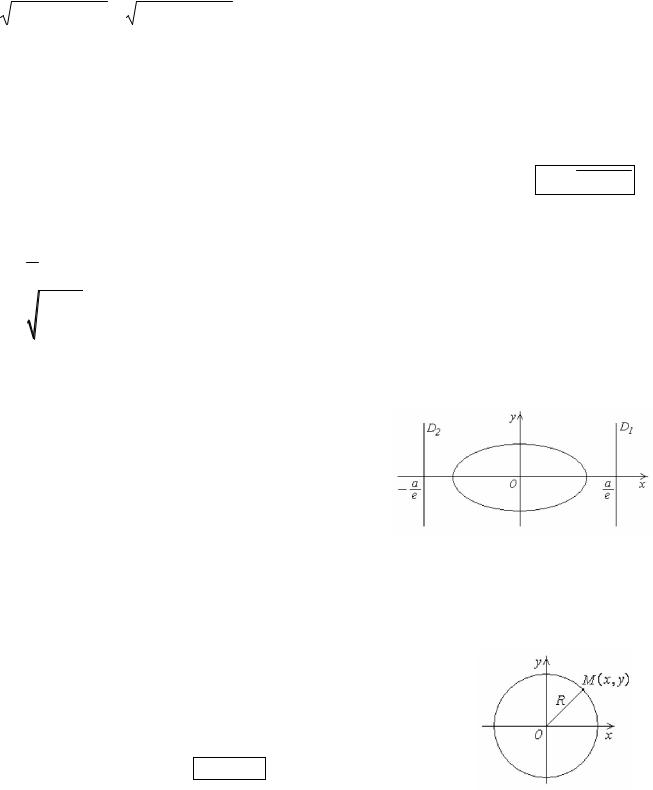
Прямые d1 |
и |
d2 , параллельные малой оси |
|
|
|
|||||
эллипса и отстоящие от его центра на |
|
|
|
|||||||
расстояниях |
d |
a |
, |
называются |
|
|
|
|||
|
|
|
|
|||||||
директрисами |
|
e |
|
|
|
|
|
|||
эллипса, |
соответствующими |
|
|
|
||||||
фокусам F1 |
и F2. Отношение расстояния любой |
|
|
|
||||||
точки эллипса до фокуса к расстоянию ее до |
|
|
|
|||||||
соответствующей директрисы постоянно и равно эксцентриситету |
r1 |
|
r2 |
e . |
||||||
d1 |
d2 |
|||||||||
|
|
|
|
|
|
|
|
|||
Окружность
Окружность представляет собой геометрическое место точек, равноудаленных от точки О, называемой центром окружности. Уравнение окружности можно получить из уравнения эллипса при a=b=R:
x2+y2=R2.
Гипербола
Гиперболой называется геометрическое место точек M(x,y), для которых абсолютная величина разности расстояний до двух заданных точек F1(+c,0) и F2(-c,0) (называемых фокусами гиперболы) постоянна и равна 2а.
31
