Часть 2 ВА и АГ интернет-материалы

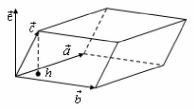
то его координаты получаются при разложении определителя по элементам первой строки.

1.6. Смешанное произведение векторов

1) a b c = b c a = c a b = – b a c = – c b a = – a c b ;

2) a b c = 0, если a 0 или (и) b 0 , или (и) c = 0, или a , b , c компланарны;

смешанное произведение трех векторов, два из которых совпадают, равно нулю.

Необходимым и достаточным условием компланарности трех векторов

объему параллелепипеда, построенного на приведенных к общему началу векторах a , b и c как на ребрах. Смешанное произведение положительно, если тройка a b c правая, и отрицательно, если тройка a b c левая. Если же векторы

12

(последнее равенство очевидно, если разложить определитель по элементам третьей строки).

13

2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Аналитическая геометрия – раздел геометрии, в котором геометрические объекты описываются алгебраическими уравнениями в декартовых (иногда иных) координатах и затем исследуются методами алгебры и анализа.

В рамках координатного метода геометрические свойства объектов выясняются путем изучения аналитическими и алгебраическими средствами свойств уравнений, описывающих геометрические объекты.

2.1. Уравнения поверхностей и линий

Уравнением поверхности называется такое уравнение, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты любой точки, не лежащей на ней:

F(x, y, z) = 0.

Сама поверхность в этом случае будет являться геометрическим образом соответствующего уравнения. В общем случае, если на три декартовы координаты точки наложено одно условие связи, у точки остаются две степени свободы, т.е., геометрический образ такого уравнения является двумерным многообразием. Одну из координат в этом уравнении, например z, можно рассматривать как неявную функцию двух других.

В частных, так называемых вырожденных случаях, геометрическим образом этой зависимости могут быть точка, линия, пустое множество. Так, образ

уравнения x2 y2 z2 R2 – сфера радиуса R с центром в точке O 0, 0,0 , об-

координаты ни одной точки пространства.

Возможно другое, параметрическое выражение функциональной зависимости между несколькими переменными с помощью вспомогательных переменных – параметров. В этом случае говорят, что поверхность задана параметрически. Так, чтобы определить положение точки на сфере, нужны два параметра, например, широта и долгота точки, лежащей на сфере. Тогда декартовы координаты точки на сфере: x R cos cos , y R cos sin , z Rsin , где R – радиус сферы.

Если уравнения F1(x, y, z) = 0 и F2(x, y, z) = 0 являются уравнениями двух поверхностей, пересекающихся по линии L, то линия L есть геометрическое место общих точек этих поверхностей, координаты которых удовлетворяют системе уравнений:

L: F1 (x, y, z) 0,

F2 (x, y, z) 0.

Вслучае двух переменных зависимость между ними F(x, y) 0 может

быть геометрически истолкована как уравнение плоской кривой. Любую величину t, определяющую положение точки (x, y) на этой кривой, можно принять за параметр. Тогда x x t , y y t дадут параметрические уравнения кривой.

14

2.2. Плоскость в пространстве Общее уравнение плоскости

Возьмем на плоскости P произвольную точку M0 (x0 , y0 , z0 ) . Выберем вектор

n {A, B,C}и M0 M {x x0 , y y0 , z z0 }, то их скалярное произведение равно

(n M0M ) A(x x0 ) B(y y0 ) C(z z0 ) .

Уравнение плоскости, проходящей через точку M 0 (x0 , y0 , z0 ) и имеющей нормальный вектор n {A, B,C}, имеет вид

A(x x0 ) B( y y0 ) C(z z0 ) 0 .

Раскрыв скобки, и обозначив Ax0 By0 Cz0 D , получим общее уравнение плоскости:

Ax By Cz D 0 .

Итак, в декартовых координатах плоскость может быть задана уравнением первой степени и представляет собой алгебраическую поверхность первого порядка.

ПРИМЕР: Составьте уравнение плоскости, проходящей через точку M (1,1,1) перпендикулярно к вектору n {2,2,3}.

Искомое уравнение примет вид: 2 x 1 2 y 1 3 z 1 0, 2x 2 y 3z 7 0 .

Если два уравнения A1x B1 y C1z D1 0 и A2 x B2 y C2 z D2 0 определяют одну и ту же плоскость, то их отличные от нуля коэффициенты пропорциональны

A1 B1 C1 D1 .

A2 B2 C2 D2

Неполные уравнения плоскостей

Рассмотрим частные случаи уравнения первой степени

Ax By Cz D 0 .

1.D = 0: Ax + By + Cz = 0.

Это уравнение определяет плоскость, проходящую через начало координат.

2.A = 0: By + Cz + D = 0. B = 0: Ax + Cz + D = 0.

C = 0: Ax + By + D = 0.

Эти уравнения определяют плоскости, параллельные соответственно координатным осям OX, OY, OZ, так как соответствующие компоненты нормального вектора плоскости равны нулю.

3.A = 0, B = 0: Cz + D = 0.

15

A = 0, C = 0: By + D = 0.

B = 0, C = 0: Ax + D = 0.

Эти уравнения определяют плоскости, параллельные соответственно координатным плоскостям OXY, OXZ, OYZ.

4.A = 0, B = 0, D = 0: Cz = 0. A = 0, C = 0, D = 0: By = 0.

B = 0, C = 0, D = 0: Ax = 0.

Эти уравнения определяют координатные плоскости XOY, XOZ,YOZ.

Уравнение плоскости «в отрезках»

Пусть коэффициенты в общем уравнении плоскости отличны от нуля. Преобразуем общее уравнение плоскости:

Ax By Cz D 0 Ax By Cz D,

Если обозначить a D ,b D ,c D , получим

A B C

уравнение плоскости «в отрезках»:

x y z 1, a b c

где a,b, c представляют собой отрезки, отсекаемые плоскостью на координатных осях.

ПРИМЕР: Какие отрезки отсекает на осях координат плоскость

2x – 4y + 6z –12 = 0 ?

Приведем общее уравнение плоскости к виду уравнения «в отрезках»

2x 4y 6z 1 x y z 1.

Пусть дана плоскость. Проведем через начало координат прямую, перпендикулярную к плоскости (нормаль), и обозначим через P точку пересечения плоскости и нормали. Обозначим углы, которые составляет нор-

ďđn OM OM n0 x cos y cos z cos .

Если известна длина отрезка OP = p, то уравнение x cos y cos z cos p

задает нормальное уравнение плоскости в виде

16

ПРИМЕР: Найдите расстояние точки M (4, 3, 1) от плоскости

3x 4y 12z 14 0 .

A2 B2 C2

Уравнение плоскости, проходящей через три данные точки

Пусть даны три точки M1 (x1 , y1 , z1 ), M 2 (x2 , y2 , z2 ), M3 (x3 , y3 , z 3 ) . Введем текущую точку плоскости M x, y,z

и рассмотрим три вектора: M1M {x x1 , y y1 , z z1},

M1M2 {x2 x1, y2 y1, z2 z1}, M1M3 {x3 x1, y3 y1, z3 z1} .

Точка M x, y,z лежит на плоскости M1M2 M3 в том и

только в том случае, если эти векторы компланарны. Условие компланарности трех векторов определяет плоскость, проходящую через три данные точки:

Угол между двумя плоскостями

Пусть плоскости P1 и P2 заданы уравнениями:

A1x B1 y C1z D1 0, A2 x B2 y C2 z D2 0.

Нормальные векторы этих плоскостей задаются координатами:

18

Один из двугранных углов между плоскостями равен острому углу между их нормальными векторами и определяется из равенства

n {A, B,C}. Из условия параллельности плоскостей:

A B C , получим A = 0, B = 1, C = - 3 и уравнение искомой плоскости

0 1 3

0 (x 7) 1 (y 2) 3 (z 3) 0 y 3z 11 0 .

ПРИМЕР: Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям:

x – y + 2z – 5 = 0, 2x + y – 3z + 1 = 0.

Нормальные векторы данных плоскостей: n1 {1, 1,2}, n2 {2,1, 3} . РЕШЕНИЕ 1:

Нормальный вектор искомой плоскости перпендикулярен к нормальным векторам данных плоскостей, т.е.

и уравнение искомой плоскости: x + 7y + 3z = 0.

19

РЕШЕНИЕ 2:

Нормальный вектор искомой плоскости перпендикулярен к нормальным векторам данных плоскостей. Из условия перпендикулярности можно найти координаты вектора n {A, B,C} из системы:

2.3. Прямая линия в пространстве

Общие уравнения прямой

Прямая линия в общем виде определяется как линия пересечения двух плоскостей, то есть системой уравнений:

A1x B1 y C1z D1 0,A2 x B2 y C2 z D2 0.

Канонические уравнения прямой

Любой ненулевой вектор раллельный ей, называется направляющим вектором прямой. Пусть - текущая точка прямой, а

Вектор M 0 M {x x0 , y y0 , z z0 } коллинеарен вектору a , следовательно, их координаты пропорциональны.

Канонические уравнения прямой, проходящей через

Параметрические уравнения прямой

Обозначим отношения, входящие в канонические уравнения прямой, через t:

Отсюда получаем параметрические уравнения прямой в виде:

Уравнения прямой в виде проекций на координатные плоскости

20

ПРИМЕР: Прямая задана общими уравнениями: 3x 2y 4z 11 0, (*)

2x y 3z 1 0.

Составьте канонические и параметрические уравнения прямой. Напишите ее уравнение в виде проекций на координатные плоскости.

Найдем координаты точки, лежащей на прямой. Положим x0 1, а две другие координаты найдем из системы (*):

В качестве направляющего вектора прямой выберем вектор, являющийся векторным произведением нормальных векторов плоскостей, линией пересечения которых будет искомая прямая.

Уравнения прямой, проходящей через две данные точки

Пусть даны две точки M1 (x1, y1, z1 ) и M2 (x2 , y2 , z2 ) . В качестве направ-

ляющего вектора прямой выберем вектор M1M2 {x2 x1, y2 y1, z2 z1}, и уравнения прямой, проходящей через две данные точки, примут вид:

ПРИМЕР: Составьте уравнения прямой, проходящей через две точки

21