b2
|
|
a |
- уравнение эллипса в полярных координатах, связанных с |
|
1 ecos |
|
|
|
фокусом;
e  a2 b2 - эксцентриситет эллипса, если координатные оси совпадают с a
a2 b2 - эксцентриситет эллипса, если координатные оси совпадают с a
осями эллипса.
Окружность
Окружность - геометрическое место точек, равноудаленных от точки О (центр).
x2 y2 R2 - уравнение окружности радиуса R с центром в
начале координат;
|
(x x )2 ( y y )2 |
R2 |
- уравнение окружности радиуса |
R |
0 |
0 |
|
); |
с центром в точке (x0,y0 |
|
x x0 |
R cost, |
- параметрические уравнения окружности радиуса R с |
|
|
Rsin t |
|
y y0 |
|
|
|
центром в точке (x0,y0);
R - уравнение окружности радиуса R с центром в начале координат в полярных координатах;
2 2 |
cos( ) 2 |
R2 |
- уравнение окружности радиуса |
0 |
0 |
0 |
|
|
R с центром в точке ( 0, 0) в полярных координатах;
2R cos - уравнение окружности радиуса R в полярных координатах. Центр окружности лежит на полярной оси, окружность касается начала координат.
Гипербола
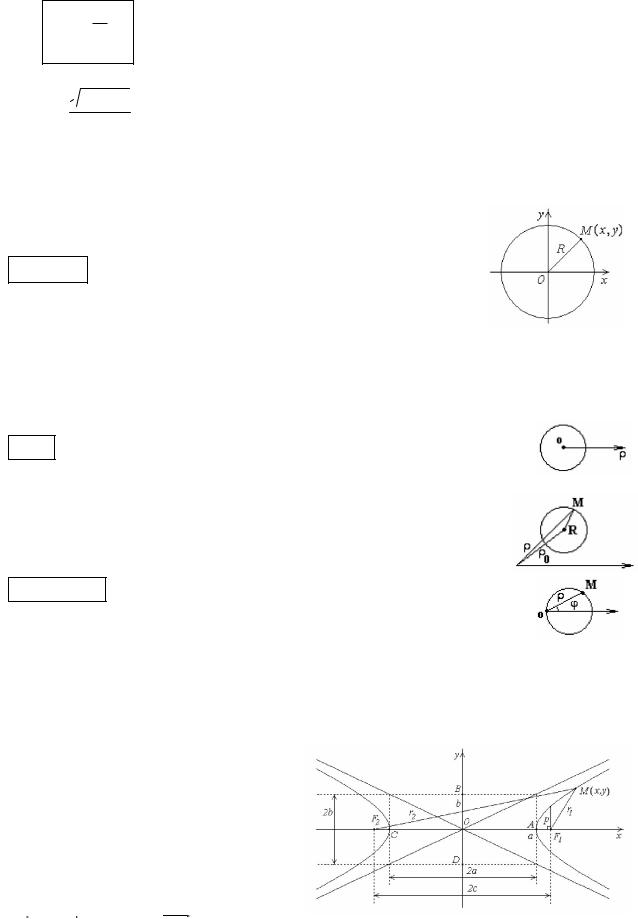
Гипербола - геометрическое место точек M x, y , для которых абсо-
лютная величина разности расстоя-
ний до |
двух заданных точек |
F1 c,0 |
и F2 c,0 (называемых |
фокусами гиперболы) постоянна и равна 2a .
|
F1M |
|
F2M |
2a и |
F1F2 |
2c , |
a c , |
c2 a2 b2 . |
|
|
|

|
x2 |
|
y2 |
1 |
- каноническое уравнение гиперболы. |
|
a2 |
b2 |
|
|
|
|
Гипербола – центральная линия второго порядка. Она состоит из двух бесконечных ветвей, симметрична относительно осей. Элементами гиперболы являются: точка О - центр гиперболы; точки А и В - вершины гиперболы;
точки F1(+ с ,0) и F2(- с ,0) - фокусы гиперболы; |
2с - фокусное расстояние, |
которое вычисляется по формуле |
c |
|
|
; AB=2a - действительная ось |
b2 a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гиперболы; CD=2b - мнимая ось гиперболы; |
|
|
|
|
; e |
c |
|
1 |
b2 |
|
, e 1 |
- |
|
b |
|
c2 a2 |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a2 |
|
эксцентриситет гиперболы.
Эксцентриситет определяется отношением осей гиперболы и характеризует еe форму: чем больше e, тем более вытянут вдоль мнимой оси основной прямоугольник гиперболы.
Асимптоты гиперболы - это прямые, к которым ветви гиперболы неограниченно приближаются при удалении в бесконечность.
|
b |
|
|
Уравнения асимптот гиперболы имеют вид: |
y |
|
|
x |
. |
|
|
a |
|
|
Угол между асимптотами зависит от значения эксцентриситета гиперболы
e |
c |
1, он определяется из уравнения |
tg |
|
|
b |
. При |
a b гипербола |
|
|
|
|
a |
2 |
|
a |
|
называется равнобочной, ее асимптоты взаимно перпендикулярны, уравнение гиперболы имеет вид: x2 y2 a2 . Если принять асимптоты за оси координат,
то уравнение гиперболы примет вид: xy a2 , то есть равнобочная гипербола
2
является графиком обратной пропорциональности. Прямые d1 и d2 , перпендикулярные
действительной оси гиперболы и отстоящие от
ее центра на расстояниях d a , называются e
директрисами гиперболы, соответствующими фокусам F1 и F2. Отношение расстояния любой точки гиперболы до фокуса к расстоянию ее до
соответствующей директрисы постоянно и равно эксцентриситету r1 r2 e . d1 d2
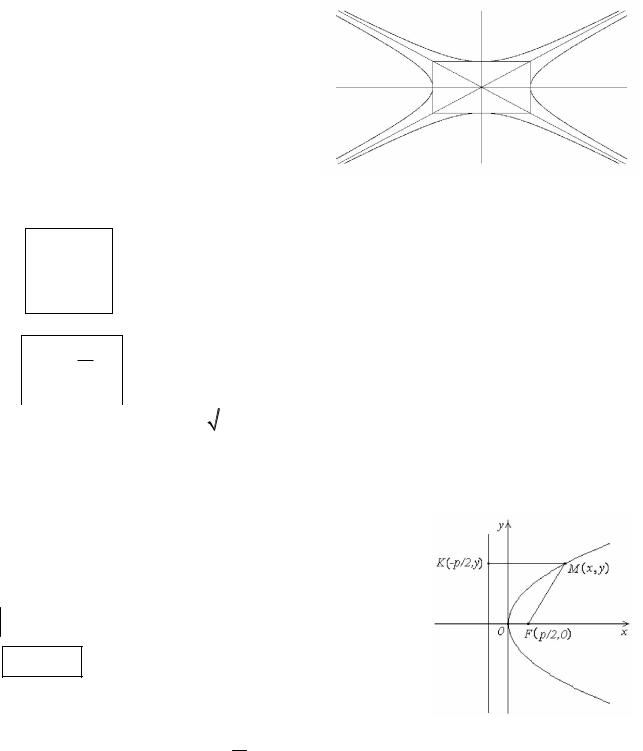
Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях a и b определяются уравнениями
|
x2 |
|
y2 |
1 |
и |
|
x2 |
|
y2 |
1 |
. |
|
a2 |
b2 |
|
a2 |
b2 |
|
|
|
|
|
|
|
|
Сопряженные гиперболы имеют общие асимптоты. Действительная ось каждой из них есть мнимая ось другой и наоборот.
x a ch t,
y bsh t, - параметрические уравнения правой ветви гиперболы; t ( , )
b2
|
|
|
a |
|
- уравнение правой ветви гиперболы в полярных координатах, |
|
1 ecos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
связанных с фокусом, e |
|
a2 |
b2 |
|
|
|
- эксцентриситет гиперболы. |
|
|
|
a
Парабола
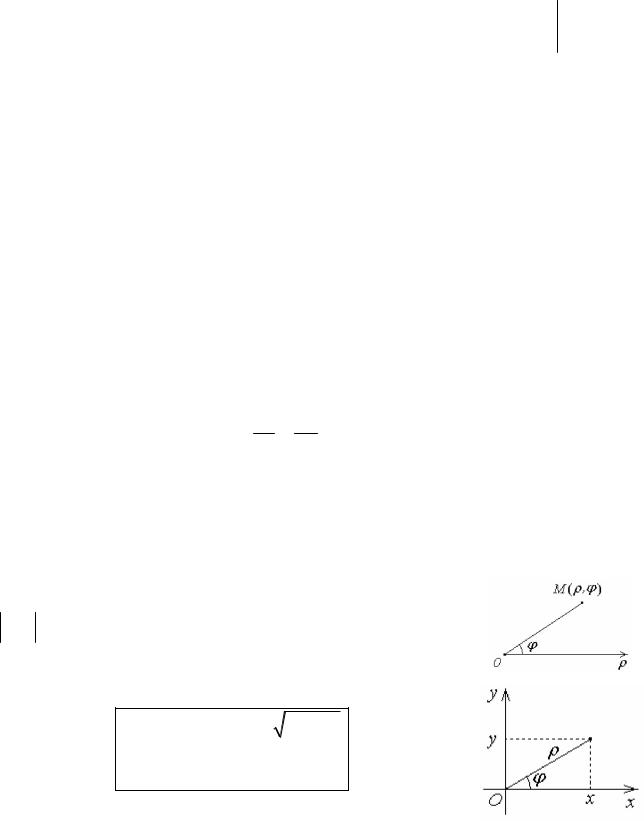
Парабола - геометрическое место точек M x, y ,
равноудалённых от заданной точки (фокуса) и от данной прямой (директрисы).
y2 2 px - каноническое уравнение параболы с
вершиной в начале координат,
точка О - вершина; OX - ось параболы;
точка F(р/2,0) - фокус; x p - уравнение директрисы;
2
e 1- эксцентриситет; p - фокальный параметр (расстояние от фокуса до директрисы или половина хорды, проходящей через фокус перпендикулярно оси OX).
(y y |
)2 2 p(x x ) |
- каноническое уравнение параболы с вершиной в |
0 |
0 |
|
точке (x0,y0);
|
|
p |
|
- уравнение параболы в полярных координатах, связанных с |
|
1 cos |
|
|
|
фокусом;
x t,
- параметрические уравнения параболы.
y  2 pt
2 pt
Уравнения вырожденных кривых второго порядка (прямые)
a2 x2 c2 y2 0, |
- |
уравнения двух пересекающихся |
y |
a |
|
x |
прямых; |
|
|
|
|
|
|
|
c |
|
|
|
|
|
- |
уравнения двух параллельных |
y2 a2 0, |
|
y a |
|
прямых; |
|
|
- уравнение двух совпадающих с осью OX прямых. |
y2 0 |
|
|
|
|
|
|
|
Преобразования координат |
|
|
|
|
|
|
Для приведения кривой Ax2 2Bxy Cy2 2Dx 2Ey F 0 к каноническому виду следует подвергнуть уравнение преобразованиям:
|
|
|
|
|
, Ŕ Ń, |
|
|
|
x x cos y sin , |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2B |
|
|
|
y x sin y cos , |
1 |
arctg |
, Ŕ Ń, |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
A C |
|
|
|
|
|
|
|
и выделить полный квадрат для определения центра кривой, |
если он существует. |
|
|
|
|
|
|
|
|
|
(x x )2 |
( y y )2 R2 |
- уравнение окружности |
с |
|
0 |
0 |
|
|
|
|
|
|
|
|
центром в точке O '(x0 , y0 ) и радиусом R;
|
(x x )2 |
|
(y y |
)2 |
1 |
- уравнения эллипса и гиперболы с центром |
|
0 |
0 |
|
|
a2 |
b2 |
|
|
|
|
|
|
симметрии в точке O'(x0, y0 );
y y0 b (x x0 ) - уравнения асимптот гиперболы; a
(y y0 )2 2 p(x x0 ) - уравнение параболы с вершиной в точке O'(x0, y0 ).
При переходе от одной системы прямоугольных координат к другой мы заменяем уравнение Ax2 2Bxy Cy 2 2Dx 2Ey F 0 линии второго порядка другим уравнением
A1x2 2B1xy C1 y2 2D1x 2E1 y F1 0 .
При этом выражения |
I A C A C |
и |
I |
2 |
A1 |
B1 |
|
A B |
1 1 1 |
|
|
B1 |
C1 |
|
B C |
|
|
|
|
|
|
остаются равными. Они называются инвариантами (неизменными) уравнения второй степени.
С их помощью различают три типа линий второго порядка.
1). Эллиптический тип, если I2 AC B2 0.
К нему относятся, кроме действительного эллипса, также мнимый эллипс
и пара мнимых прямых, пересекающихся в действительной точке
2). Гиперболический тип, если I2 AC B2 0.
К нему относится, кроме гиперболы, пара действительных
x2 y2
пересекающихся прямых a2 b2 0.
3). Параболический тип, если I2 AC B2 0.
К нему относится, кроме параболы, пара параллельных (действительных или мнимых) прямых (они могут совпадать).
Линии в полярной системе координат
Полярные координаты
OM , 0 , 0 2 .
Связь полярных координат с декартовыми
Для M(x,y) и M( , ):
|
x cos , |
|
x2 y2 , |
|
|
|
|
y |
|
|
y sin , |
tg |
. |
|
|
x
Окружности
a cos , а=const >0. |
2 a sin , а=const >0. |
Спирали
Архимедова спираль: a , 0 , 0 .
Гиперболическая спираль: a , 0 , 0 , a > 0.
Логарифмическая спираль: a , a 0, a 1; - < , 0 .
167
Розы
Двухлепестковые розы:
a sin 2 , a>0; 0 2 , 0 a ; |
a cos 2 , a>0; |
0 2 , 0 a . |
Четырехлепестковые розы a > 0
a |
sin 2 |
; |
0 2 , |
0 a ; |
a |
cos 2 |
; |
0 2 , |
0 a . |
Трёхлепестковые розы:
a sin 3 ;0 2 , 0 a, a>0 ; a cos 3 ; 0 2 , 0 a, a>0 .
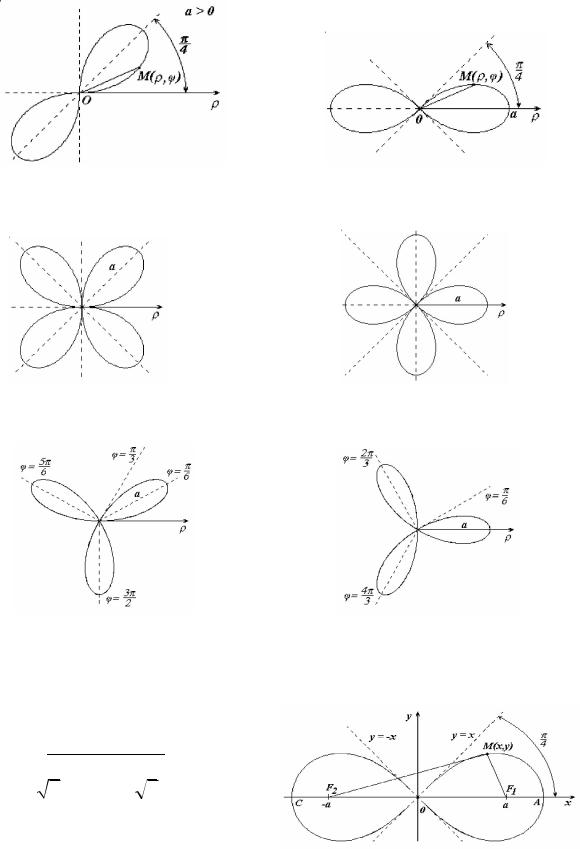
Лемниската Бернулли
2 2a2 cos2
Вершины кривой находятся в точках A(a
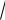 2,0); C( a
2,0); C( a
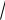 2,0).
2,0).
Площадь каждой петли S = a2.
Кардиоида
В полярных координатах a(1 cos ), a 0. Вершина кардиоиды находится в точке А (2а,0).
Укажем, что площадь кардиоиды S 3 a2 , 2
а длина L= 8a.
Параметрическое задание линий Окружность
x R cos t, |
- параметрические уравнения |
|
y R sin t |
окружности. |
|
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
x2 y2 R2 (cos2 t sin2 t) R2 .
Циклоида |
|
x a(t sint), |
где |
|
y a(1 cost), |
|
t . |
|
При 0 t 2 получаем первую арку циклоиды. Укажем, что длина дуги одной арки
L 8a , а площадь под одной аркой S 3 a2 .
Астроида
x Rcos3 t,
где 0 t 2 . В декартовых
y Rsin3 t,
координатах уравнение астроиды x2/3+y2/3=R2/3. Длина астроиды L= 6R, а площадь, ограниченная
астроидой, S = 3 R2/8.
169
IV. Поверхности второго порядка
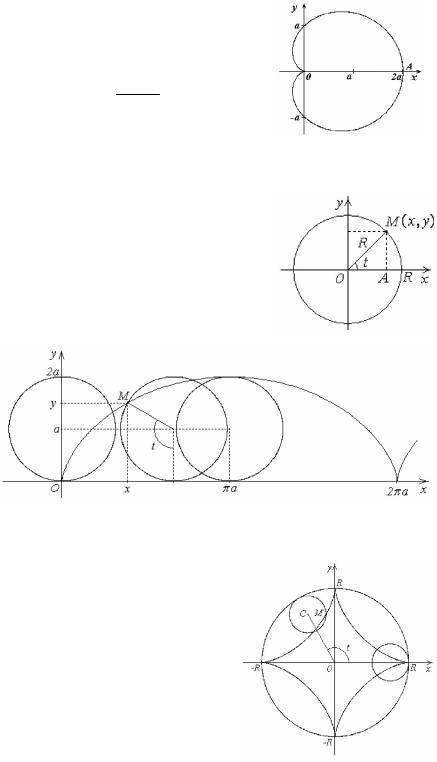
Эллипсоид
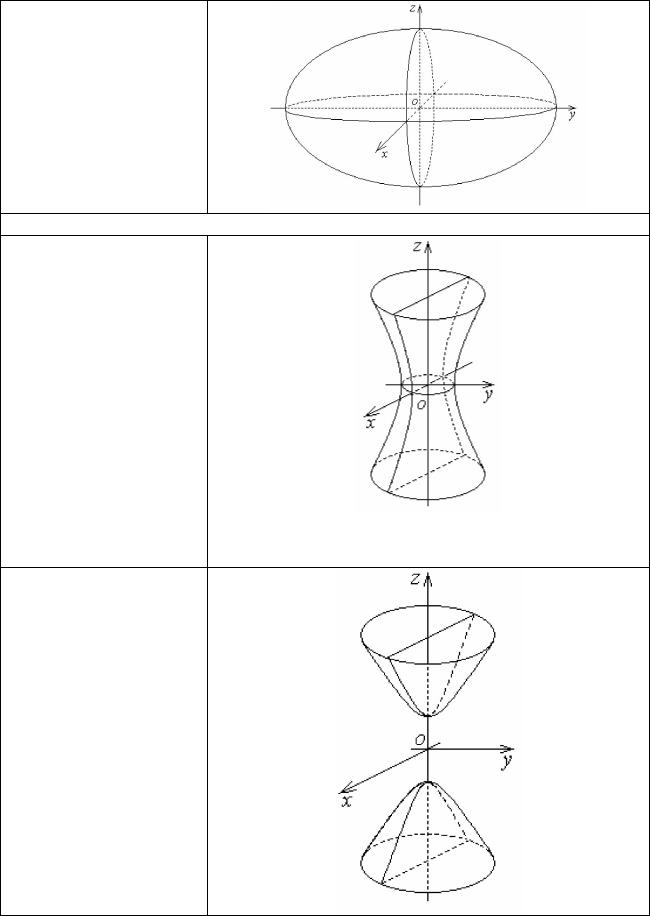
Гиперболоиды
Однополостный гиперболоид
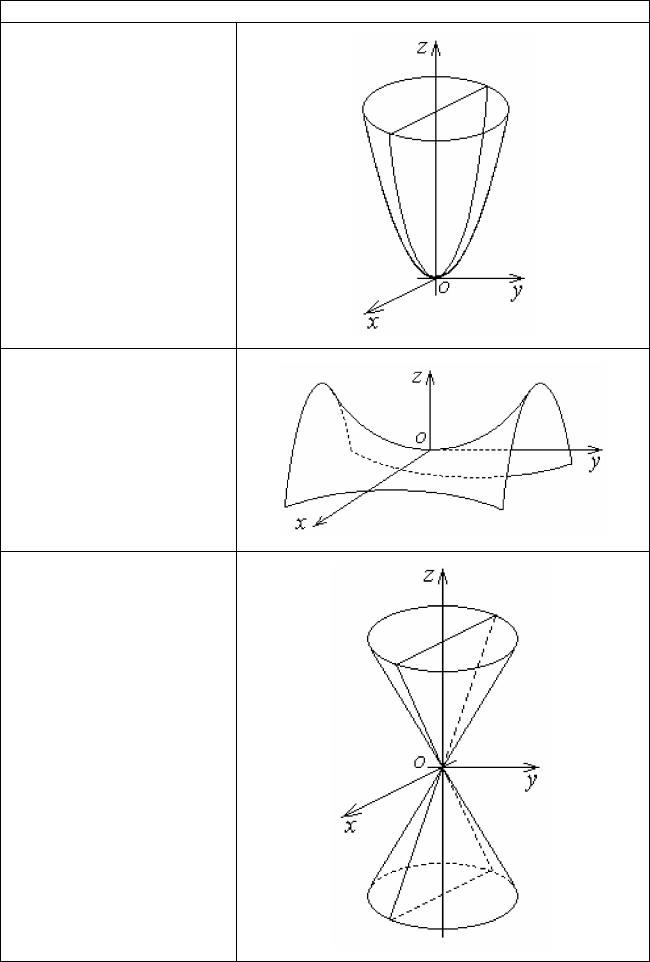
Двуполостный гиперболоид
Параболоиды
Эллиптический параболоид
Гиперболический параболоид
Конус второго порядка









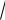 2,0);
2,0); 
 2,0).
2,0).