Вариант 20
1. Дан правильный шестиугольник OABCDE со стороной ОА = 3.
Обозначим OA m , AB n и BC p . Установите зависимость между ними. Выразите через m и n векторы OB , BC , ED , OD , DA .
2. Докажите, что если диагонали четырехугольника в точке пересечения делятся пополам, то этот четырехугольник - параллелограмм.
3. Найдите длину вектора a 3c d , если c 2, d 6, а угол между векторами c и d равен 60 .
4. Найдите уравнения и длины сторон и медиан треугольника если даны две его вершины А (-1, 2), В (-11, 7) и точка М (19/3;8/3) пересечения его медиан.
5. Постройте кривую y 5 3x .
6. Приведите кривую 10 x 2 4 3 xy 6 y 2 0 к каноническому виду.
7. Найдите точку, симметричную точке M 1;2;0 относительно плоскости P : 4x 5y z 7 0.
8. Найдите угол между плоскостями 6 x 2 y 4 z 17 0 ,
9x 3y 6z 4 0 .
9. Вычислите кратчайшее расстояние между прямыми:
x
y 3
z 2
,
x 1
y 2
z
.
1
2
0
0
1
2
5x 4y 3z 3 0,
10. Составьте уравнения проекции прямой на
4 x y z 2 0,
плоскость 5 x 3 y 2 z 5 0 .
11. Составьте уравнение сферы, если известно, что точки
M 1 2;3;3 ,M 2 2;1;1 ,M 3 0;3;1 ,M 4 2;3; 1 лежат на сфере.
x2
y2
12. Найдите уравнения линий пересечения поверхности
3z
4
6
с координатными плоскостями.
142
Вариант 21
1. Вне плоскости параллелограмма ABCD взята точка О . В базисе из векторов OA , OB , OC найти координаты вектора OK , если К –
середина стороны AD .
2. Найти направляющие косинусы вектора a 1; 2; 2 .
3. Составляют ли векторы a 1; 1; 1 , b 2; 1; 3 , c a , b
ортогональный базис трехмерного пространства?
4. Найдите уравнения и длины сторон и медиан треугольника, если даны три его вершины А (1; -2), В (-9; 3), С (-5; -5).
5. Постройте кривую x 2 15 y 2 2 y .
6. Приведите кривую 6 x 2 4 3 xy 10 y 2 1 0 к каноническому виду.
7. Найдите точку, симметричную точке M 2; 1;1 относительно плоскости P : x y 2z 2 0.
8. Точка M 2;1; 3 служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составьте уравнение этой плоскости.
9. Найдите проекцию точки М (2;1;0) на плоскость P : y + z + 2 = 0.
10. Докажите, что прямая L : x y 2 z лежит в плоскости
1 2 1
x y 3 z 2 0 .
11. Составьте уравнение сферы, если известны координаты ее центра
C (1;-2;0) и радиус R = 3.
x2
y2
z2
12. Найдите уравнения линий пересечения поверхности
1
4
9
25
с координатными плоскостями.
143
Вариант 22
1. В плоскости треугольника АВС найдите точку О такую, что
OA OB OC 0 . Существуют ли такие точки вне плоскости треугольника?
2. Векторы a и b неколлинеарны. При каких значениях скалярной
величины векторы a b
и 3a b коллинеарны?
3. Образуют ли базис в пространстве векторы {1; 0; 0},
1
1
1
1
0;
;
,
0;
;
? Будет ли он ортонормированным?
2
2
2
2
4. Найдите вершины и уравнения медиан треугольника, если даны уравнения трех его сторон AC : x 2 y 3 0 ; AB : x 2 y 5 0 ;
BC : 2 x y 19 0 .
5. Постройте кривую y 2 4 24 x 2 2 x .
5
6. Приведите кривую 5 x 2 2 3 xy 3 y 2 0 к каноническому виду.
7. Найдите точку, симметричную точке M 1;1;1 относительно плоскости
P : x 4 y 3z 5 0.
8. Укажите значение λ , при котором плоскости P 1 : x 3 y 2 z 5 0 и
P 2 : 3 x 3 y 3 z 8 0 будут перпендикулярны.
9. Составьте уравнения прямой, образованной пересечением плоскости 2 x y 3 z 4 0 с плоскостью, проходящей через ось абсцисс и
точку A 2; 1;3 .
x y z 2 0,
10. Найдите точки пересечения прямой L :
x y 3 z 6 0
с координатными плоскостями.
11. Составьте уравнение сферы, если известны координаты ее центра
C (2;-1;3) и точки M (0;1;2) на сфере.
x2
y2
z2
12. Найдите уравнения линий пересечения поверхности
1
9
16
4
с координатными плоскостями.
Вариант 23
1. Даны 3 точки A x 1 ; y 1 ; z 2 , B x 2 ; y 2 ; z 2 , C x 3 ; y 3 ; z 3 , не лежащие на одной прямой. Найдите координаты точки пересечения медиан треугольника АВС .
2. Найдите направляющие косинусы вектора a 2b , если
a 2 i 3 j 4 k, b i j k .
3. Вычислите: 1) a b , 2a 2b 3a 3b , 4a 4b ;
2)
[[a b , 2a 2b ],
[3a 3b , 4a 4b ]]
.
4. Найдите уравнения и длины сторон треугольника, если даны две его вершины А (1; 2), В (21; -8) и точка К (13; 8) пересечения его высот.
4
5.
Постройте кривую x 2
y 2 2y 10.
3
6. Приведите кривую 11 x 2 2 3 xy 9 y 2 1 0 к каноническому виду.
7. Найдите точку, симметричную точке M 1;2;3 относительно плоскости P : 2x 10y 10z 1 0.
8. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям 2 x 2 y 2 z 1 0,
3x 2y 3z 4 0.
x 5 y 2 z 5 0,
9. Докажите, что прямая пересекает ось ординат .
x y z 1 0
10. Составьте уравнения прямых, образованных пересечением плоскости 3 x 5 y z 4 0 с координатными плоскостями.
11. Составьте уравнение сферы, если известно, что точки M 1 1; 2;5 и
M 2 3; 2; 1 - концы ее диаметра.
12. Найти уравнения линий пересечения поверхности x 2 y 2 z 2 1 L :
25 16 9
с координатными плоскостями.
145
Вариант 24
1. В трапеции ABCD длины оснований AD и BC относятся как 4 : 1. Принимая за начало координат вершину А , а за базисные векторы AD и AB , найдите координаты вершин трапеции и точки S пересечения боковых сторон.
2. Найдите единичный вектор, сонаправленный вектору a 2i 3 j 6k .
3. Какой угол образуют единичные векторы c 0 и d 0 , если известно, что
векторы a 3c 4d и b c d ортогональны?
4. Найдите координаты вершин треугольника, если даны уравнения двух его сторон AC : x 2 y 5 0 , AB : x 2 y 3 0 и двух высот:
2x 4y 10 0, 2x y 14 0.
5. Постройте кривую x 2 5 y .
6. Приведите кривую 9 x 2 2 3 xy 11 y 2 1 0 к каноническому виду.
7. Найдите точку, симметричную точке M 0; 3; 2 относительно плоскости P : 2x 10y 10z 1 0.
8. Составьте уравнение плоскости, которая проходит через точку
M (1;-1;4) перпендикулярно к двум плоскостям: x 2 y z 5 0, и
y x 0.
9. Составьте уравнение плоскости, проходящей через прямую
x
y 3
z 2
перпендикулярно к плоскости
3 x y 2 z 0.
1
2
0
x
y1
z
10. Найдите угол между прямыми L :
и
2
1 7
1
x 5 y 2 z 5 0,
2 :
x y z 1 0.
11. Составьте уравнение сферы, если известны координаты ее центра C
(1;1;0) и то, что плоскость 2 x 3 y 3 z 1 0 касается сферы.
12. Найдите уравнения линий пересечения поверхности z x 2 y 2 1 L
4
с координатными плоскостями.
Вариант 25
1. Дан треугольник АВС . На стороне ВС расположена точка М так, что |BM | : |MC | = λ . Найдите вектор AM , если AB b , AC c .
2.
Даны векторы a 2; 0;1 ,
b 1;1; 0 , c 0;1;
3 . Вычислите
прc [ a, b ].
3.
Даны векторы a 2; 3;1 ,
b 3;1; 2 , c 1; 2;
3 . Вычислите
[ [a ,b ],c ] и [a ,[b ,c ]] .
4. Найдите уравнения и длины сторон и медиан треугольника, если даны две его вершины А (-1; -2), В (19; -12) и точка М (29/3; -10/3)
пересечения его медиан.
5. Постройте кривую x 2 1 y .
6. Приведите кривую 5 x 2 2 3 xy 7 y 2 8 0 к каноническому виду.
7. Найдите точку, симметричную точке M 1;0; 1 относительно плоскости P : 2 y 4z 1 0.
8. Определите двугранный угол, образованный пересечением пары
плоскостей 5 x - 3 y 2 z 5 0,
3x 3y -3z -8 0.
9. Вычислите кратчайшее расстояние между прямыми:
x 1
y - 2
z 2
,
x -1
y - 2
z
.
2
2
1
0
0
1
3x y 3 0,
на
10. Составьте уравнения проекции прямой L :
x 2 y 5z 10 0,
плоскость P : x y 3 z 5 0 .
11. Составьте уравнение сферы, если известно, что точки
M 1 2; 5;1 , M 2 1; 2; 1 , M 3 1; 5;2 , M 4 1; 8; 1 лежат на сфере.
x2
y2
12. Найдите уравнения линий пересечения поверхности
2z
2
4
с координатными плоскостями.
8. ПРИМЕР ВАРИАНТОВ КОНТРОЛЬНЫХ РАБОТ Векторная алгебра
1.
На векторах a 3 i j , b 5 i 2 k построен параллелограмм. Найдите площадь
параллелограмма и длины его диагоналей.
2.
Найдите пр b a , если a 2 e 1 e 2 , b e 1 e 2 , где
e1
1,
e2
2, e 1
e 2 600 .
3.
Вычислите объем тетраэдра: A 3,2,4 , B 2, 3, 4 , C 2, 2,3 , D 0, 2,1 .
4.
На плоскости заданы векторы e 1 2,1 , e 2 1,1 , a 5,2 . Можно ли взять
e 1 , e 2 за новый базис на плоскости? Если да, то найдите разложение вектора a
по базису и запишите соответствующее разложение.
5.
Убедитесь, что векторы a 4 i 3 j , b 5 k могут быть взяты за ребра куба.
Найдите третье ребро c .
Аналитическая геометрия
1. Найдите расстояние от точки М 0 до плоскости, проходящей через точки
М 1 , М 2, М 3 , если М 1 (-3,4,-7), М 2 (1,5,-4), М 3 (-5,-2,0), М 0 (-12,7,-1).
2. Напишите уравнение плоскости, проходящей через точку A (1,0,-2) перпендикулярно вектору BŃ , если известны координаты точек B (2,-1,3),
C (0,-3,2).
3. Найдите угол между плоскостями x – 3y + 5 = 0 и 2x – y + 5z – 16 = 0.
4. Найдите координаты точки A (0,0,z ), равноудаленной от точек B (5,1,0) и
C (0,2,3).
5. Напишите каноническое уравнение прямой, по которой пересекаются плоскости 2 x + y + z – 2 = 0 и 2x – y – 3z + 6 = 0.
x 2 y 3 z 1
6. Найдите точку пересечения прямой 1 1 4 и плоскости x +2y +3z -14 = 0.
7. Установите, какую кривую второго порядка определяет уравнение 4 x 2 +3 y 2 – 8x + 12y – 32 = 0. Найдите для эллипса и гиперболы
координаты центра, полуоси, эксцентриситет и уравнения директрис, для параболы – координаты вершины и величину параметра p .
x2
2
z2
8. Найдите
точки пересечения поверхности
y
1
и прямой
9
4
x 3
y 1
z 6
3 . Укажите тип поверхности.
1
1
148
9. ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
I. Векторная алгебра
Вектор - направленный отрезок.
Векторы называются коллинеарными , если лежат на одной прямой либо на параллельных прямых.
Три вектора называются компланарными , если они лежат в одной плоскости или в параллельных плоскостях.
Два вектора равны , если они коллинеарны, имеют одинаковую длину и направление.
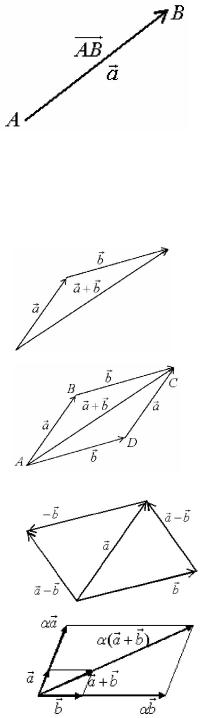
Линейные операции над векторами
Суммой a b двух векторов a и b называется вектор, идущий из начала вектора a в конец вектора
b
при условии,
что начало вектора b приложено к
концу вектора a (правило треугольника).
Свойства:
1˚.
a b
b a
2˚.
a b c a
b c
3˚.
a 0 a
вектора a существует вектор
4˚.
Для
каждого
a , такой, что a a 0 .
Разностью векторов a и b будет вектор a b , идущий из конца вектора b к концу вектора a .
Произведение a вектора a на вещественное число обладает свойствами:
6˚. a a a
7˚. a a
8˚. 1 a a
Базис и координаты
Базисом в пространстве называются три некомпланарных вектора, взятые в определенном порядке.
Базисом на плоскости будем называть два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.
Базисом на прямой будем называть любой ненулевой вектор этой прямой.
Каждый вектор может быть разложен по базису в пространстве и это разложение единственно.
Коэффициенты разложения вектора по базису называются координатами вектора в данном базисе и в каждом базисе определяются однозначно:
d a b
c = , , .
При сложении двух векторов d 1
и d 2 их координаты (относительно любо-
го базиса) складываются. При умножении вектора d 1 на любое число все его координаты умножаются на это число.
Системой координат в пространстве называют совокупность базиса
и некоторой точки О , называемой началом координат.
a , b ,
c
Вектор OM , идущий из начала координат в точку M , называется радиусвектором точки M .
Координатами точки M , , называются координаты вектора OM .
Таким образом, координаты радиус-вектора OM и координаты точки M совпадают.
Ортонормированный базис. Декартова прямоугольная система координат
Пусть в качестве базиса выбраны три взаимно перпендикулярных вектора с длинами, равными единице.
Обозначения: i, j,k , i = j = k 1 .
Такой базис называется ортонормированным (ОНБ).
Векторы i , j , k называются базисными ортами. Зафиксируем точку О – начало координат и отложим от нее векто-
ры i , j , k . Полученная система координат называется
прямоугольной декартовой.
X
Координаты любого вектора в этом базисе называются декартовыми координатами вектора:
Прямые линии, проведенные через начало координат по направлениям
базисных векторов, называются координатными осями: i – порождает OX ;
j – порождает OY ;
k – порождает OZ . Координаты точки М (вектора OM ) в
декартовой системе координат по осям OX , OY ,
OZ называются соответст-
венно абсциссой, ординатой и аппликатой.
вектора a равны проекци-
Декартовы прямоугольные координаты x , y , z
ям этого вектора на оси Ox , Oy , Oz соответственно; другими словами,
x ďđ OX a
a
cos , y ďđOY a
a
cos , z ďđOZ a
a
cos .
Здесь , , – углы, которые составляет вектор a с положительными направлениями координатных осей Ox , Oy , Oz соответственно, при этом
cos , cos , cos
Вектор a 0
называются направляющими косинусами вектора a .
a
cos , cos , cos представляет собой вектор единичной a
длины данного направления, или орт данного направления. Для направляющих косинусов справедливо соотношение:
cos2 cos2
cos2 1.
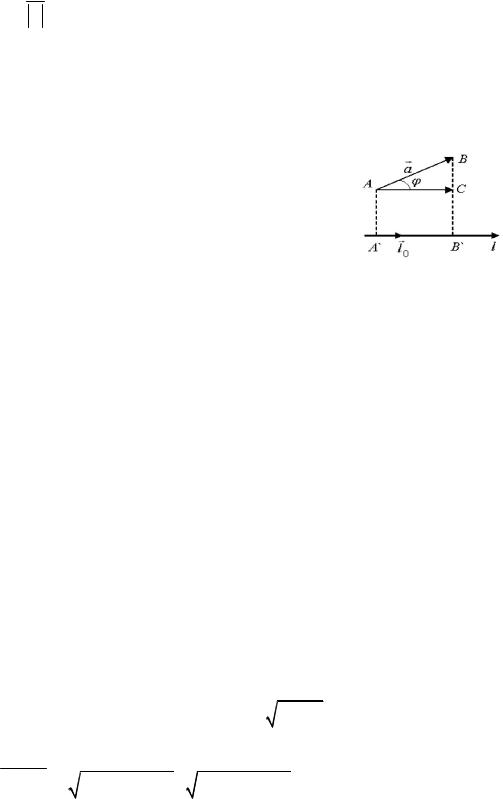
Проекция вектора a на ось l A B
равна
cos
- орт оси l .
прl a
a
a
cos(a , l 0 ) , где l 0
Если a x 1 ,
y1 , z1
и b x 2 ,
y 2 , z 2 коллинеарны, то
x1
y1
z1
.
x2
y2
z2
Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
b
a
b a, b a b
a
cos(a , b ) .
Если a x 1 ,
y 1, z 1 ,
b x2 ,
y 1 y 2 z 1z 2 .
y2 , z2 , то a b x1 x2
Алгебраические и геометрические свойства скалярного произведения:
1°. a b b a .
2°. a b a b a b
.
3°. a b c
a
c
b c ,
a
b c a b
a
c
0 , и a a
0
4°. a a 0 , если a
, если a 0 .
2
o
2
5°. a a
a
a
a
cos0
a
;
a
a a .
cos a , a
a b
x 1 x 2
y 1 y 2 z 1 z 2
6°. cos a , b
.
a
b
x 1 2 y 1 2 z 1 2
x 2 2 y 2 2 z 2 2
2x .
3 xy 6 y2 0 к каноническому виду.
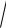15 y2 2 y.
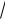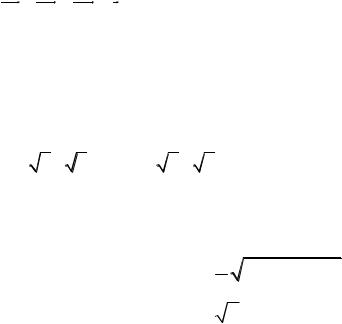
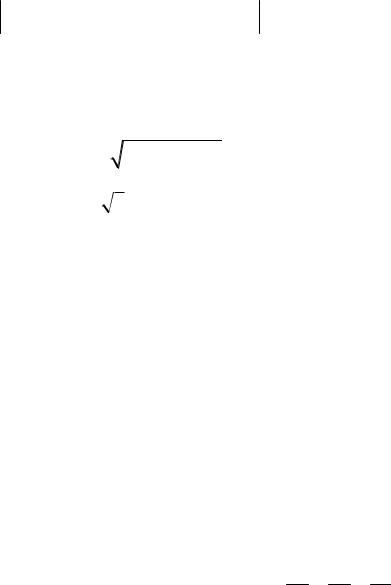
3 xy 10y2 1 0 к каноническому виду.
3 xy 9y2 1 0 к каноническому виду.
