
Часть 2 ВА и АГ интернет-материалы
.pdf
|
Какую линию определяет уравнение x2 + y2 = x? |
|
|||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
Запишем уравнение в виде x2 – x + y2 = 0. |
|
|||||||
|
Выделим полный квадрат из слагаемых, содержащих |
|
|||||||
16 |
х: |
|
|
|
|
|
|
|
Окружность |
x2 – x = (x – 1/2)2 – 1/4. |
1 2 |
|
|
|
|
|
|||
|
|
|
2 |
|
1 |
|
|
||
|
Уравнение принимает вид x |
|
|
y |
|
|
|
|
|
|
|
|
4 |
|
|
||||
|
|
2 |
|
|
|
|
|
||
|
и определяет окружность с центром в точке (1/2, 0) и |
|
|||||||
|
радиусом 1/2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Преобразования координат
Преобразуйте уравнение гиперболы x2 – y2 = 1 поворотом осей на 45 против часовой стрелки.
РЕШЕНИЕ:
|
Так как = -45 , то cos |
2 2, sin 2 2. |
|||
|
Отсюда преобразование поворота принимает вид: |
||||
|
|
|
|
|
|
|
2 2 x y , |
|
|||
17 |
x |
|
|||
|
|
|
|
|
|
2 2 y x . |
|
||||
|
y |
|
|||
|
|
|
|
|
|
Подстановка в исходное уравнение дает х у = 1/2. Так выглядит уравнение гиперболы в новой системе координат и дает график обратно-пропорциональной зависимости, знакомой из курса школьной математики.
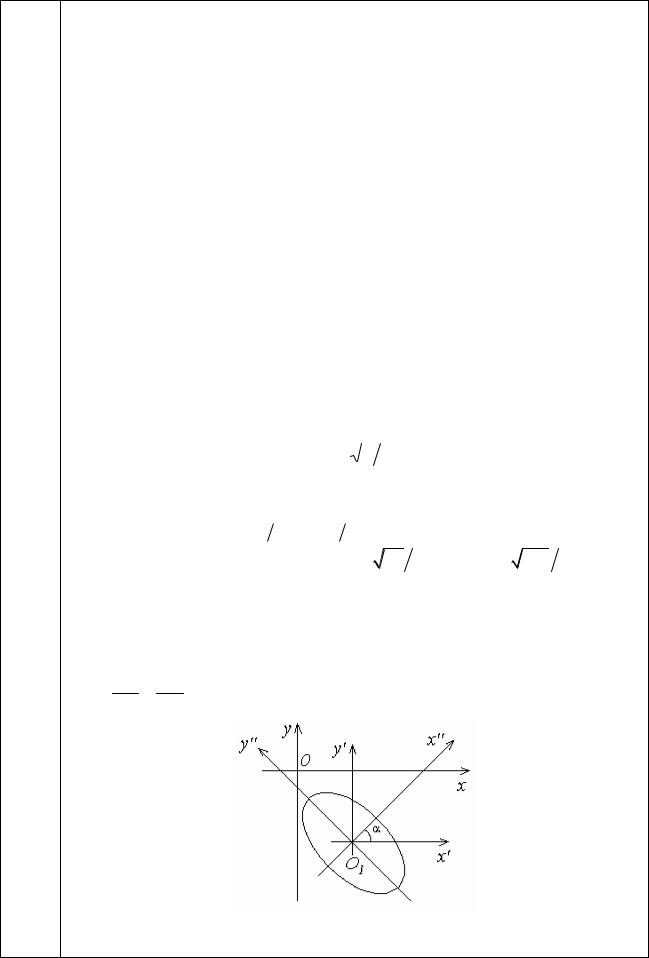
Установите, какую линию определяет уравнение x2 + y2 + xy – 2x + 3y = 0.
РЕШЕНИЕ:
1). Перенесем начало координат в такую точку О1(х0, у0), чтобы уравнение не содержало х и у в первой степени.
Это соответствует преобразованию координат:
x x x0 , 18
y y y0.
Подстановка в исходное уравнение дает
(x + x0)2 + (x + x0)(y + y0) + (y + y0)2 – 2(x + x0) + 3(y + y0) = 0 или x 2 + x y + y 2 + (2x0 + y0 - 2)x + (x0 + 2y0 + 3)y + x02 +
+ x0y0 + y02 - 2x0 + 3y0 =0.
Положим 2x0 + y0 – 2 = 0, x0 + 2y0 + 3 = 0.
Решение полученной системы уравнений: x0 = 7/3 и y0 = -8/3 дает
92
координаты нового начала координат O1(7/3, -8/3), а уравнение после преобразований принимает вид x 2 + x y + y 2 = 93/25.
2). Повернем оси координат на такой угол , чтобы исчез член х у . Подвергнем последнее уравнение преобразованию:
x x cos y sin ,
y x sin y cos
и получим (cos2 + sin cos + sin2 ) x 2 + (cos2 - sin2 ) x y + + (sin2 - sin cos + cos2 ) y 2 = 93/25.
Полагая cos2 - sin2 = 0, имеем tg2 = 1.
Следовательно, 1,2 = 45 .
Тот же результат можно получить из формулы
|
|
|
|
|
|
|
|
|
|
|
|
Ŕ Ń, |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2B |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ŕ Ń. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
, |
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A C |
|
|
|
|
||||||||
В этом примере À Ñ 1 и |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Возьмем = 45 , cos45 = sin45 = |
|
|
|
2. |
|
|
|
|
|||||||||||||||||||
2 |
|
|
|
|
|||||||||||||||||||||||
После соответствующих вычислений получаем |
|
|
|
||||||||||||||||||||||||
|
3 |
x 2 |
1 |
y 2 |
93 |
|
|
x 2 |
|
|
|
|
y 2 |
|
|
1 |
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
62 25 |
186 25 |
|
|
|
|
||||||||||||||||||||
2 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
- уравнение эллипса с полуосями a |
|
5 1,5 |
и b |
|
5 2,7 в |
|||||||||||||||||||||
|
62 |
186 |
|||||||||||||||||||||||||
дважды штрихованной системе координат, получаемой из исходной параллельным переносом осей координат в точку О1(7/3, -8/3) и последующим поворотом на угол 45 против часовой стрелки.
Итак, уравнение x2 + y2 + xy – 2x + 3y = 0 приведено к каноническому
x 2 y 2
виду a2 b2 1.
93

Приведите к каноническому виду уравнение
4x2 – 4xy + y2 – 2x – 14y + 7 = 0.
РЕШЕНИЕ:
1). Система уравнений для нахождения центра кривой:
|
4x0 2 y0 |
1 0, |
|
|
несовместна, |
|
2x0 y0 7 0 |
|
значит, данная кривая центра не имеет.
2). Не меняя начала координат, повернем оси на некоторый угол , соответствующие преобразования координат имеют вид:
x x cos y sin ,
y x sin y cos .
|
Перейдем в уравнении к новым координатам: |
|
||||||||||||||
|
4x2 – 4xy + y2 – 2x – 14y + 7 = (4cos2 - 4cos sin + sin2 ) x 2 + |
|
||||||||||||||
|
+ 2 (-4sin cos - 2cos2 + 2sin2 + sin cos ) x y + 2 (-cos - 7sin ) x + |
|||||||||||||||
|
+ (4sin2 + 4sin cos + cos2 ) y 2 |
+ 2 (sin - 7cos ) y + 7 = 0. |
(*) |
|||||||||||||
|
|
Постараемся теперь подобрать угол так, чтобы коэффициент |
||||||||||||||
|
при х у обратился в нуль. Для этого нам придется решить |
|||||||||||||||
19 |
тригонометрическое уравнение: |
|
|
|
||||||||||||
- 4sin cos - 2cos2 + 2sin2 + sin cos = 0. |
|
|||||||||||||||
|
Имеем 2sin2 - 3sin cos - 2cos2 = 0, или 2tg2 - 3tg - 2 = 0. |
|
||||||||||||||
|
Отсюда tg = 2, или tg = -1/2. |
|
|
|
||||||||||||
|
Такой же результат получается из общей формулы |
|
||||||||||||||
|
|
1 |
arctg |
2B |
, |
Ŕ 4, |
Ń 1, |
2Â 4 |
|
|||||||
|
|
|
|
|||||||||||||
|
2 |
|
|
A C |
|
|
|
|
|
|
|
|||||
|
tg 2 |
2 tg |
|
4 |
, |
tg |
|
2, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 tg |
2 |
|
3 |
0,5. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Возьмем первое решение, которое соответствует повороту осей на острый угол. Зная tg , вычислим cos и sin :
cos |
1 |
|
|
1 |
, |
sin |
|
tg |
|
2 |
. |
||||
|
|
|
|
|
|
|
|
|
|
||||||
1 tg2 |
5 |
|
|
1 tg2 |
5 |
|
|
||||||||
|
|
|
|
|
|||||||||||
Отсюда, и учитывая (*), находим уравнение данной кривой в системе
х , у :
5y 2 6
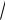 5x 2
5x 2
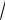 5y 7 0. (**)
5y 7 0. (**)
3). Дальнейшее упрощение уравнения (**) производится при помощи параллельного перенесения осей Ох , Оу .
Перепишем уравнение (**) следующим образом:
94
|
2 |
|
5 |
|
|
|
|
|
|||||
5 y |
|
2 |
|
y 6 5x 7 0. |
||
|
|
|||||
|
|
|
5 |
|
||
|
|
|
|
|||
Дополнив выражение в первой скобке до полного квадрата разности и компенсируя это дополнение надлежащим слагаемым, получим
|
|
|
|
2 |
|
6 |
|
|
|
|
|
|
|
5 |
|
5 |
5 |
||||||||||
y |
|
|
|
|
|
|
|
|
x |
|
|
|
0. |
5 |
|
5 |
|
|
5 |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
Введем теперь еще новые координаты х ,у , полагая
x = x + 5 5, |
y = y + 5 5, |
что соответствует параллельному |
перемещению осей на величину |

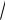 5
5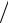 5 в направлении оси Ох и на величину
5 в направлении оси Ох и на величину 
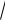 5
5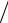 5 в направлении оси
5 в направлении оси
Оу . В координатах х у уравнение данной линии принимает вид
y 6
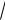 5 x 2. 5
5 x 2. 5
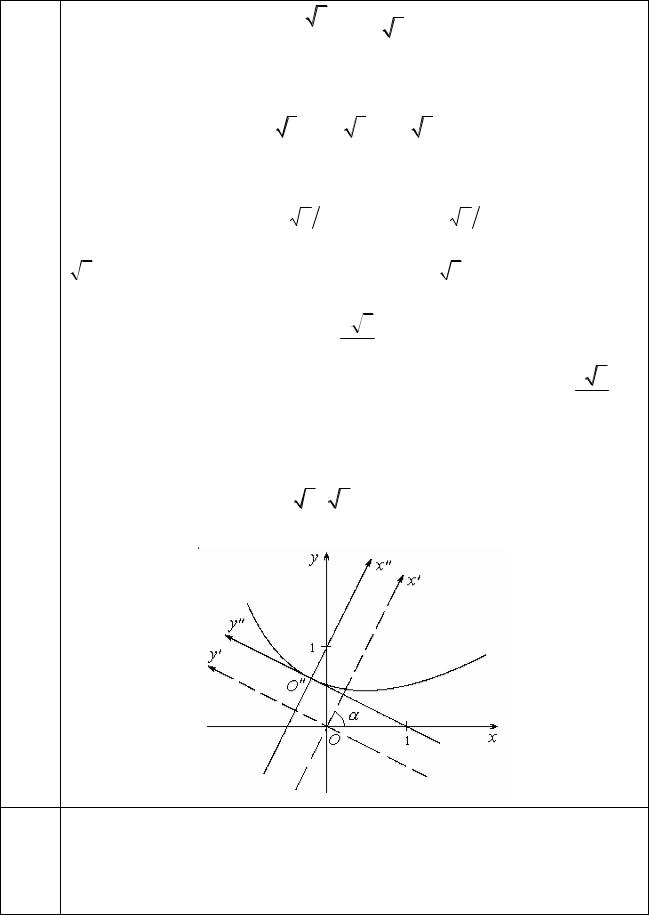
Это есть каноническое уравнение параболы с параметром p 3 5 и с
5
вершиной в начале координат системы O '' x '' y ''. Парабола
расположена симметрично относительно оси х и бесконечно простирается в положительном направлении этой оси. Координаты
|
5 |
|
5 |
|
|
|
1 |
|
3 |
|
|
вершины в системе х у O '' |
|
; |
|
, а в системе ху O '' |
|
|
|
; |
|
|
. |
|
|
|
|
||||||||
|
5 |
|
5 |
|
|
5 |
|
5 |
|
||
|
|
|
|
|
|
|
|
||||
Какую линию определяет уравнение
4x2 - 4xy + y2 + 4x - 2y - 3 =0?
20 РЕШЕНИЕ:
Система для нахождения центра кривой в данном случае имеет
вид
95

|
|
|
|
|
|
4x0 2 y0 2 0, |
||||||||
|
|
|
|
|
|
|
|
1 0. |
||||||
|
|
|
|
|
|
2x0 y0 |
||||||||
|
Эта система равносильна одному уравнению |
|||||||||||||
|
2х0 – у0 + 1 = 0, следовательно, линия имеет |
|||||||||||||
|
бесконечно много центров, |
|
|
|
|
|||||||||
|
составляющих прямую 2х – у + 1= 0. |
|||||||||||||
|
Заметим, что левая часть данного уравнения |
|||||||||||||
|
разлагается на множители первой степени: |
|||||||||||||
|
4х2 – 4ху + у2 + 4х –2у –3 = (2х – у +3)(2х – у – 1). |
|||||||||||||
|
Значит, рассматриваемая линия представляет собой |
|||||||||||||
|
пару параллельных прямых: |
|
|
|
|
|||||||||
|
2х – у +3 = 0 и 2х – у – 1 = 0. |
|
|
|||||||||||
|
Какую линию определяет уравнение |
|||||||||||||
|
|
|
|
|
|
5х2 + 6ху + 5у2 – 4х + 4у + 12 = 0? |
||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
||||||
|
Уравнение 5х2 + 6ху + 5у2 – 4х + 4у + 12 = 0 |
|||||||||||||
|
приводится к каноническому виду: х 2 + 4у 2 + 4 = 0, или |
|||||||||||||
|
|
2 |
|
y |
2 |
|
|
|
|
|
|
|
|
|
21 |
|
x |
|
|
1. |
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
Это уравнение похоже на каноническое уравнение эллипса. Однако |
|||||||||||||
|
оно не определяет на плоскости никакого действительного образа, так |
|||||||||||||
|
как для любых действительных чисел х ,у левая часть его не |
|||||||||||||
|
отрицательна, а cправа стоит –1. Такое уравнение называется |
|||||||||||||
|
уравнением мнимого эллипса. |
|
|
|||||||||||
|
Какую линию определяет уравнение |
|||||||||||||
|
|
|
|
|
|
5х2 + 6ху + 5у2 – 4х + 4у + 4 = 0? |
||||||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
||||||
|
Уравнение 5х2 + 6ху + 5у2 – 4х + 4у + 4 = 0 |
|||||||||||||
22 |
приводится к каноническому виду: х 2 + 4у 2 = 0, или |
|||||||||||||
|
|
|
|
|
|
2 |
|
y |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
|
|
0. |
|||
|
|
|
|
|
|
4 |
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
Уравнение похоже на каноническое уравнение эллипса, но определяет |
|||||||||||||
|
не эллипс, а единственную точку: х = 0, у = 0 – вырожденный эллипс. |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
4. Кривые на плоскости |
||||||||
|
|
|
||||||||||||
|
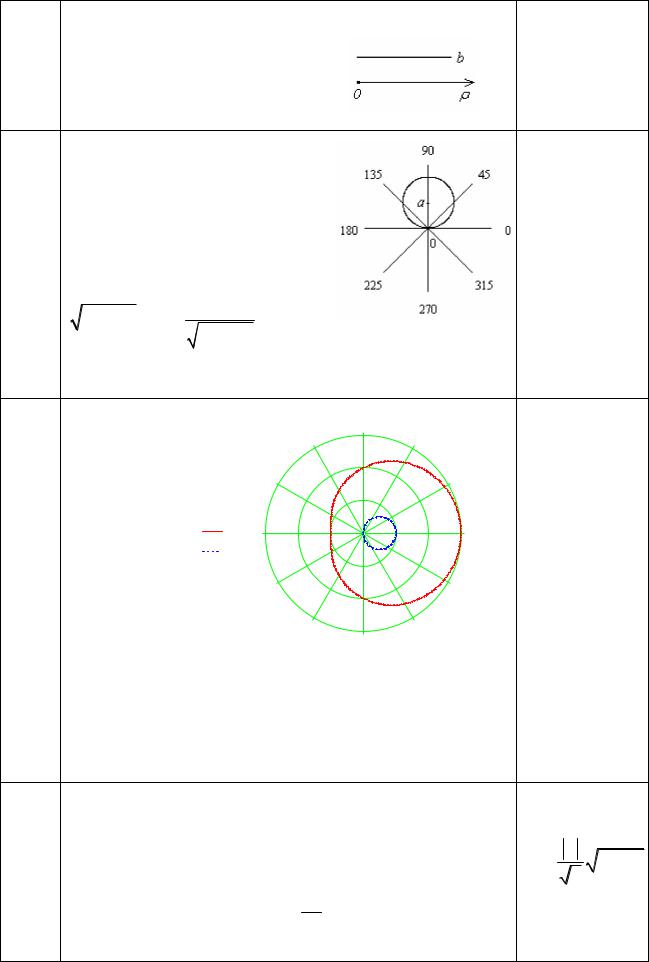
Найдите полярное уравнение кривой x = a, a > 0 и |
|
||||||||||||
|
изобразите ее. |
|
|
|
|
|
|
|
||||||
23 |
РЕШЕНИЕ: |
|
|
|
|
|
|
= a/cos |
||||||
|
cos = a = a/cos : |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
96
|
Найдите полярное уравнение кривой |
|
|
|||||
24 |
y = b, |
b > 0 и изобразите ее. |
|
|
|
|||
РЕШЕНИЕ: |
|
|
|
|
= b/sin |
|||
|
sin = b = b/sin : |
|
|
|
||||
|
Постройте в полярной системе |
|
|
|
||||
|
координат линию = |
2a sin , |
|
|
|
|||
|
a > 0. |
|
|
|
|
|
|
|
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
Линия |
представляет |
собой |
|
|
|
||
25 |
окружность |
со |
смещенным |
|
Окружность |
|||
|
центром: |
|
y |
|
|
|
|
|
|
x2 y2 2a |
, |
|
|
|
|||
|
|
|
x2 y2 |
|
|
|
|
|
|
x2 + y2 – 2ay = 0, |
|
|
|
|
|
||
|
x2 + (y – a)2 = a2. |
|
|
|
|
|
||
|
Постройте |
в |
|
|
90 |
|
|
|
|
полярной |
|
|
|
|
|
||
|
|
|
120 |
|
60 |
|
||
|
системе |
|
|
|
|
|
|
|
|
координат |
|
|
150 |
|
30 |
|
|
|
линию = 2 |
|
|
|
|
|
||
|
+ cos . |
|
cos(t) 2 |
|
|
0 |
|
|
|
РЕШЕНИЕ: |
|
180 |
|
|
|||
|
|
cos(t) |
|
|
|
|
||
|
|
|
|
|
|
|
||
26 |
Линия |
|
|
|
|
|
Улитка Пас- |
|
представляет |
|
210 |
|
|||||
|
|
330 |
|
|||||
|
|
|
каля |
|
||||
|
собой улитку |
|
|
|
|
|||
|
|
|
|
|
|
|||
|
Паскаля и |
|
|
240 |
|
300 |
|
|
|
|
|
|
270 |
|
|
||
|
получается, |
|
|
|
|
|
||
|
|
|
|
t t |
|
|
||
|
если каждый |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
радиус-вектор окружности |
|
|
|
||||
|
= cos увеличить на два. Найдем координаты |
|
||||||
|
контрольных точек: |
|
|
|
|
|||
|
= 0, = 3; = /2, = 2; = , = 1. |
|
|
|||||
|
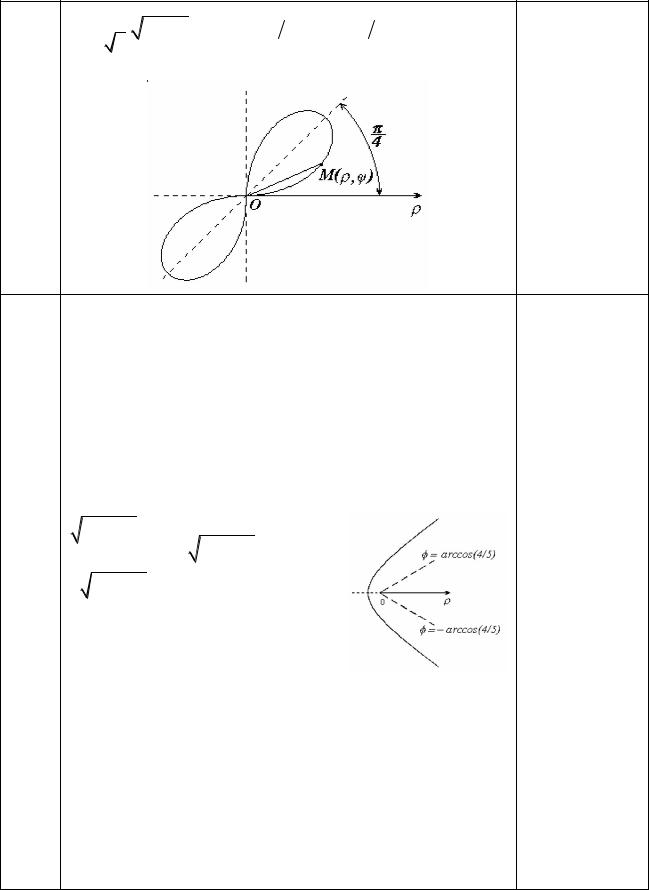
Найдите полярное уравнение кривой |
|
|
|||||
|
(х2 + у2)2 = а2ху и изобразите ее. |
|
|
|||||
|
РЕШЕНИЕ: |
|
|
|
|
|
a |
|
27 |
ОДЗ: |
xy 0. |
|
|
|
sin 2 |
||
|
|
|
|
2 |
||||
|
4 a2 2 cos sin 2 a2 |
sin 2 , |
sin 2 0 . |
|
||||
|
|
|
|
|
2 |
|
|
|
|
Уравнение кривой в полярных координатах имеет вид: |
|
||||||
97
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
и задает |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
sin 2 , |
|
|
0, |
2 |
|
, 3 2 |
|
||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
двухлепестковую розу:
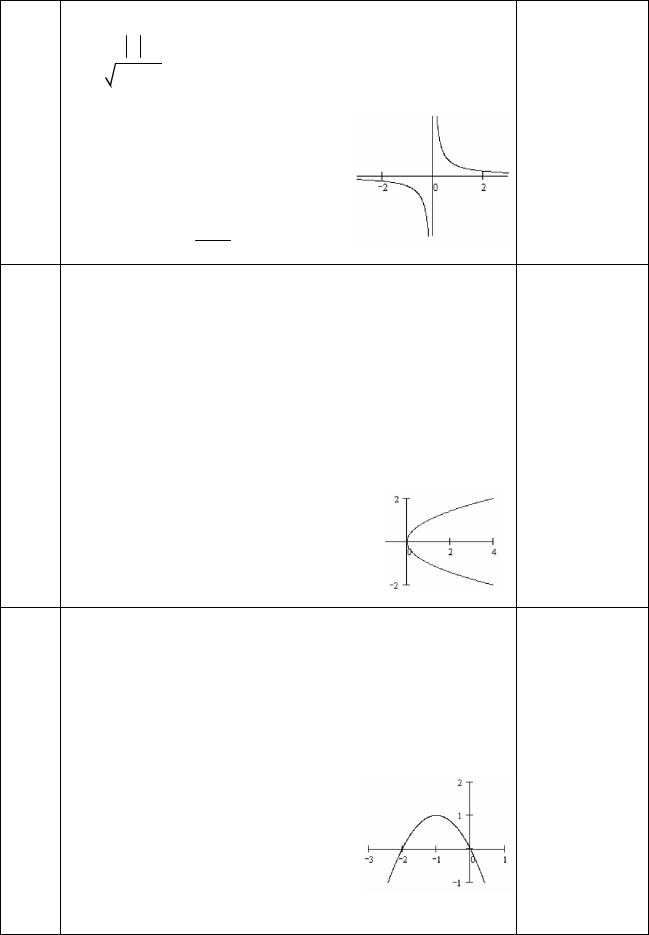
Постройте в полярной системе координат линию
|
9 |
. |
|
||
|
4 5cos |
|
РЕШЕНИЕ:
4 – 5 cos > 0, cos < 4/5,
(arccos(4/5), 2 – arccos(4/5)).
При этом (4 - 5 cos ) = 9.
Переходя к декартовым координатам, получаем
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 |
4 5 |
|
|
|
|
|
|
|
9, |
|
|
|
|
|
Правая |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||||||||
28 |
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
ветвь гипер- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
болы |
||||||
|
4 x2 y2 |
5x 9, |
|
|
|
|
|
|
|
|
|
|||||||||
|
16 x2 y2 5x 9 2 , |
|
|
|
|
|
|
|
|
|||||||||||
|
16x2 + 16y2 = 25x2 + 90x + 81, |
|
|
|
|
|
|
|||||||||||||
|
9x2 + 90x – 16y2 +81 = 0, |
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
(x 5) |
2 |
|
y2 |
||||||
|
9(x + 5) |
– 16y |
|
|
= 144 |
|
|
|
|
|
|
|
1 – правая |
|||||||
|
|
|
|
4 |
2 |
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
ветвь гиперболы при указанных . |
|
|
|
|
|||||||||||||||
|
Кривую можно было построить по точкам, например, |
|||||||||||||||||||
|
при = |
= 9/10. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
Постройте в полярной |
системе |
координат линию |
|||||||||||||||||
29 |
2 sin2 = а2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Гипербола |
|||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
98
sin 2 0, 0, 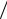 2 , 3
2 , 3 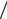 2 .
2 .
a
 .
. 
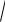 sin 2
sin 2
Перейдем к декартовым координатам, учтем, что
sin 2 2cos sin |
2 |
|
2xy |
, |
||
2 |
x2 |
y2 |
||||
|
|
|
||||
тогда кривая принимает |
вид |
|||||
гиперболы: y a2 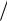 2. x
2. x
Какая линия задается параметрическими уравнениями:
x 3cost,
t 0, 2 ?
y 2sin t,
30 РЕШЕНИЕ: |
Эллипс |
|
|
x2 |
y2 |
|
|
|
|||
|
|
|
|
|
|
|
1 - эллипс. |
||
|
|
2 |
2 |
2 |
|||||
|
3 |
|
|
|
|
|
|||
|
|
||||||||
|
Какая линия задается параметрическими уравнениями: |
||||||||
|
|
|
2 |
2t 1, |
t R ? |
||||
|
|
|
|
||||||
31 |
x t |
|
|
||||||
y t 1, |
Парабола |
||||||||
РЕШЕНИЕ:
у2 = x – парабола.
Какая линия задается параметрическими уравнениями:
|
|
|
|
|
x 1 2cost, |
0, 2p ? |
|
|
|
t |
|
32 |
|
|
Окружность |
y 3 2sin t, |
|||
|
РЕШЕНИЕ: |
|
|
|
(x + 1)2 + (y – 3)2 = 4 – окружность. |
||
|
Какая линия задается параметрическими уравнениями: |
||
|
x 2t 1 , |
t R ? |
|
|
|
|
|
|
y 1 4t2 |
, |
|
33 |
РЕШЕНИЕ: |
Парабола |
|
|
y = – x2 – 2x, y = – (x + 1)2 +1 |
||
|
– парабола с вершиной в точке |
||
|
(-1, 1). |
|
|
99

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 4
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
|
Установите тип поверхности, заданной уравнением |
|
|||||||||||
|
x2 y2 z2 4 0. |
|
|
|
|
|
|
|
|
||||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
||
1 |
Перенесем константу в правую часть уравнения и раз- |
Двуполостный |
|||||||||||
делим обе части уравнения на число 4. Получим |
|||||||||||||
гиперболоид |
|||||||||||||
|
|
|
|
x2 |
|
z2 |
|
y2 |
|
|
|
||
|
|
|
|
|
|
1. |
|
|
|||||
|
|
|
4 |
|
|
|
|
|
|||||
|
|
|
4 |
4 |
|
|
|
|
|||||
|
Это уравнение задает двуполостный гиперболоид |
|
|||||||||||
|
вращения с осью OY. |
|
|
|
|
|
|
|
|
||||
|
Установите тип поверхности, заданной уравнением |
|
|||||||||||
|
x2 y2 z 2. |
|
|
|
|
|
|
|
|
|
|
||
|
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
|
||
2 |
Преобразуем уравнение к виду |
|
|
Параболоид |
|||||||||
|
|
|
x2 |
y2 |
(z 2), |
|
|||||||
|
являющемуся канонической формой уравнения пара- |
|
|||||||||||
|
болоида вращения с осью OZ, вершина которого нахо- |
|
|||||||||||
|
дится в точке (0;0;2), а выпуклость обращена вверх. |
|
|||||||||||
|
Установите тип указанной поверхности и постройте |
|
|||||||||||
|
ее: |
|
|
|
|
|
|
|
|
|
|
1) параболоид |
|
|
1) x2 y2 |
z 2 0 ; |
|
|
|
|
|
||||||
|
2) |
x2 y2 |
0 ; |
|
|
|
|
|
|
|
вращения; |
||
|
3) |
x2 y2 |
0 ; |
|
|
|
|
|
|
|
2) ось oz; |
||
|
|
|
|
|
|
|
|
3) две пересе- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
кающиеся |
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости |
|
3 |
4) |
x2 1; |
|
|
|
|
|
|
|
|
|
x y ; |
|
|
|
|
|
|
|
|
|
|
|
4) две плоско- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
сти x 1, па- |
|
|
|
|
|
|
|
|
|
|
|
|
|
раллельные |
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости zoy; |
|
|
5) x2 z2 |
1. |
|
|
|
|
|
|
|
5) круговой ци- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
линдр с обра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
зующей, парал- |
|
|
|
|
|
|
|
|
|
|
|
|
|
лельной оси oy. |
|
|
Составьте уравнения проекций на координатные плос- |
|
|||||||||||
|
кости |
сечения |
эллиптического |
параболоида |
x2 4xy 5 y2 x 0 |
||||||||
4 |
x y2 |
z2 плоскостью x 2y z 0. |
|
x2 2xz 5z2 4x 0 |
|||||||||
РЕШЕНИЕ: |
|
|
|
|
|
|
|
|
|
y2 z2 2y z 0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
Сечение параболоида плоскостью задается системой |
|
|||||||||||
|
уравнений |
|
|
|
|
|
|
|
|
|
|
||
100

x y2 z2 ,
x 2y z 0.
Этой системе соответствует некоторая линия в пространстве. Чтобы найти проекцию этой линии на координатную плоскость OXY, следует исключить из этой системы переменную z. В результате получаем x2 4xy 5y2 x 0.
|
Аналогично находятся остальные проекции: |
|
|
|||
|
на плоскость OXY: x2 4xy 5y2 x 0 ; |
|
|
|||
|
на плоскость OXZ: |
x2 2xz 5z2 4x 0 ; |
|
|
||
|
на плоскость OYZ: y2 z2 2y z 0. |
|
|
|||
|
|
|
|
|||
|
Составьте уравнение поверхности, образованной вра- |
|
|
|||
|
|
x |
2 |
, |
|
|
|
z |
|
|
|
||
|
|
|
|
вокруг оси OX. |
|
|
|
щением кривой |
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0 |
|
|
|
||
|
РЕШЕНИЕ: |
поверхности плоскостью x x0 , |
|
|
||
5 |
Сечение искомой |
y2 z2 |
x4 . |
|||
|
перпендикулярной оси вращения, есть окружность с |
|
|
|||
|
центром в точке C(x0 ,0,0) радиусом R z(x0 ). Урав- |
|
|
|||
|
нение этой окружности y2 z2 x 4.Для произволь- |
|
|
|||
|
|
|
|
0 |
|
|
ного x0 получаем уравнение поверхности вращения y2 z2 x4.
Найдите общие точки поверхности x2 y2 z2 4x 6y 2z 67 0
и прямой |
|
x 5 |
|
y |
|
z 25 |
. |
|
|
3 |
|
|
|
||||
РЕШЕНИЕ: |
2 |
|
2 |
|
||||
|
|
|
|
|
|
|
||
Выделим полные квадраты переменных в уравнении поверхно- |
||||||||
сти и увидим, что она представляет собой сферу |
|
|||||||
x 2 2 y 3 2 z 1 2 92 . |
Нет |
|||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 5 3t, |
|
|
|
|
|
|
|
|
|
y 2t, |
Перейдем к параметрическим уравнениям прямой |
||||||||
z 25 2t.
Подстановка этих значений переменных в уравнение поверхности приводит к квадратному уравнению для t c отрицательным дискриминантом. Следовательно, действительных значений t не существует, и поверхность не имеет общих точек с прямой, которая проходит вне сферы.
101
