- •1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу.
- •Задача 2
- •1. Рассчитаем сначала парные коэффициенты корреляции:
- •2. Коэффициенты парной корреляции я уже нашел:
- •3. Нескорректированный коэффициент множественной детерминации
- •Задача 3
- •2. К данной системе уравнений, для оценки структурных параметров коэффициентов применим дмнк.
- •Задача 4
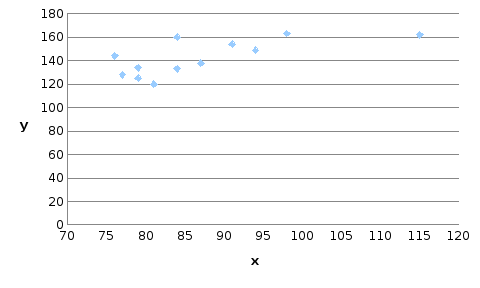
- •1.Построим поле корреляции:
- •2. Проведу выравнивание исходных уровней ряда методом скользящей средней, для этого составлю вспомогательную таблицу:
Воронков М.А.
Группа ЭМЗ-301304
Эконометрика
Индивидуальные задания
Вариант № 5
Задача 1
1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу.
|
|
|
|
|
|
|
|
|
|
|
1 |
79 |
134 |
10586 |
6241 |
17956 |
135 |
-1 |
0,74 |
|
2 |
91 |
154 |
14014 |
8281 |
23716 |
146 |
8 |
5,19 |
|
3 |
77 |
128 |
9856 |
5929 |
16384 |
133 |
-5 |
3,9 |
|
4 |
87 |
138 |
12006 |
7569 |
19044 |
143 |
-5 |
3,62 |
|
5 |
84 |
133 |
11172 |
7056 |
17689 |
140 |
-7 |
5,26 |
|
6 |
76 |
144 |
10944 |
5776 |
20736 |
132 |
12 |
8,3 |
|
7 |
84 |
160 |
13440 |
7056 |
25760 |
140 |
20 |
12,5 |
|
8 |
94 |
149 |
14006 |
8836 |
22201 |
149 |
0 |
0 |
|
9 |
79 |
125 |
9875 |
6241 |
15625 |
135 |
-10 |
8 |
|
10 |
98 |
163 |
15974 |
9604 |
26569 |
153 |
10 |
6,13 |
|
11 |
81 |
120 |
9720 |
6561 |
14400 |
137 |
-17 |
14,16 |
|
12 |
115 |
162 |
18630 |
13225 |
26244 |
169 |
-7 |
4,32 |
|
Итого |
1045 |
1710 |
150223 |
92375 |
246324 |
1712 |
-2 |
72,12 |
|
Ср.знач. |
87,08 |
142,5 |
12518,58 |
7697,91 |
20527 |
- |
- |
6,01 |
|
|
10,72 |
14,85 |
- |
- |
- |
- |
- |
- |
|
|
114,98 |
220,75 |
- |
- |
- |
- |
- |
- |
b=
(12518,58-142,5 87,08)/(7697,91-
87,08)/(7697,91-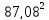 )=109,68/114,98=0,953
)=109,68/114,98=0,953
a=
142,5-0,953 87,08=59,51
87,08=59,51
y=
59,51+ 0,953 x
x
C увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,953 руб.
2.Тесноту линейной связи оценит коэффициент корреляции:
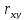 =0,953
=0,953
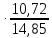 =0,687;
=0,687;
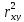 =
0,47.
=
0,47.
Это означает, что 47% вариации заработной платы(у) объясняется вариацией фактора х- среднедушевого прожиточного минимума.
Качество модели определяет средняя ошибка аппроксимации:
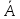 =72,12/12=6,01%
=72,12/12=6,01%
Качество
построенной модели оценивается как
хорошее, так как
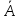 не превышает 8-10%.
не превышает 8-10%.
3.Оценку значимости уравнения регрессии в целом проведем с помощью F- критерия Фишера. Фактическое значение F-критерия:
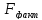 =
=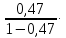 10=8,86
10=8,86
Табличное
значение критерия при пятипроцентном
уровне значимости и степенях свободы
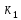 =1
и
=1
и
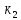 =10
составляет
=10
составляет
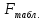 =4,96.
Так как
=4,96.
Так как
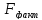 >
>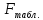 ,
то уравнение регрессии признается
статистически значимым.
,
то уравнение регрессии признается
статистически значимым.
Оценку статистической значимости параметров регрессии проведем с помощью t- статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.
Табличное
значение t-критерия
для числа степеней свободы df=10
и α=0,05 составит
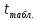 =2,23.
=2,23.
Определим
случайные ошибки
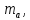
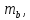
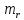 :
:
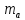 =
=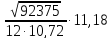 =26,41;
=26,41;
 =
=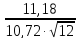 =0,301;
=0,301;
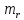 =
=
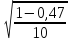 =0,23.
=0,23.
Тогда
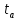 =59,51/26,41=2,25;
=59,51/26,41=2,25;
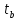 =
0,953/0,301=3,16;
=
0,953/0,301=3,16;
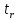 =0,687/0,23=2,98.
=0,687/0,23=2,98.
Фактические значения t-статистики превосходят табличное значение:
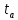 >
>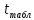 ;
;
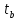 >
>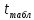 ;
;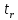 >
>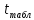 ,
поэтому параметры а, b,
и
,
поэтому параметры а, b,
и
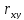 не случайно отличаются от нуля, а
статистически значимы.
не случайно отличаются от нуля, а
статистически значимы.
Рассчитаем доверительные интервалы для параметров регрессии а и b. Для этого определим предельную ошибку для каждого показателя:
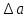 =2,23
=2,23 26,41=58,89;
26,41=58,89;
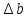 =2,23
=2,23 0,301=0,67.
0,301=0,67.
Доверительные интервалы
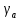 =59,51
=59,51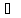 58,89;
58,89;
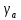 =59,51-58,89=0,62;
=59,51-58,89=0,62;
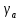 =59,51+58,89=118,4;
=59,51+58,89=118,4;
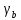 =
0,953
=
0,953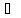 0,67;
0,67;
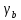 =0,283;
=0,283;
 =1,623.
=1,623.
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью p=1- α=0,95 параметры a и b , находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
4.Полученные
оценки уравнения регрессии позволяют
использовать его для прогноза. Если
прогнозное значение прожиточного
минимума составит:
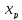 =
=
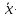 1,07=87,08
1,07=87,08 1,07=93,17
руб., тогда прогнозное значение заработной
платы составит:
1,07=93,17
руб., тогда прогнозное значение заработной
платы составит: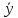 =59, 51+ 0,953
=59, 51+ 0,953 93,17=
148,3 руб.
93,17=
148,3 руб.
5.Ошибка прогноза составит:
m
= 11,18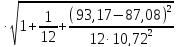 =11,75
=11,75
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:
 =2,23
=2,23 11,75=26,2.
11,75=26,2.
Доверительный интервал прогноза:
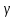 =148,3
=148,3
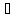 26,2;
26,2;
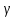 =
122,1 руб.;
=
122,1 руб.;
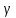 =174,5
руб.
=174,5
руб.
Выполненные прогноз среднемесячной заработной платы является надежным и находится в пределах от 122,1 руб. до 174,5 руб.
6.В заключении решения задачи построим на одном графике исходные данные и теоретическую прямую.