3.4 Неозначений інтеграл. Основні методи інтегрування.

Якщо задана деяка функція F(x), тоді її похідною є інша функція f(x), тобто

F′(x)= f(x) (*)

Сформулюємо обернену задачу: як, знаючи функцію f(x), знайти таку іншу функцію F(x), щоб виконувалась рівність (*). Відповідь на таке питання можливо отримати шляхом знаходження так званої первісної для f(x), і цією функцією буде саме F(x). Математично цю дію записують як

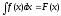
Наприклад, 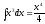. Перевіримо правильність знайденої первісної:, тобто рівність (*) в конкретному випадку справджується.

Всі можливі первісні для функції f(x) відрізняються між собою на деяку константу С, С € R. Загальне сімейство всіх первісних вигляду F(x)+C для функції f(x) утворює відповідь неозначеного інтеграла для цієї ж функції f(x),тобто

(**)

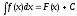Зауваження. Первісна F(x) для f(x) не завжди існує, а якщо існує, то ця первісна завжди єдина незалежно від способу її знаходження.

Наприклад, для f(x)= первісної не існує.

На основі рівності (**) складена таблиця неозначених інтегралів основних елементарних функцій.

1;

2;

3;

4;

5;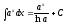

5*;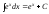

6;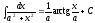

7;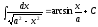

8;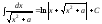

9 ;

9* ;

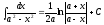10 ;

11.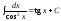

Властивості неозначеного інтеграла:

а)

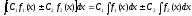
б)

в)

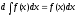
г) Якщо 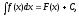тоді для будь-якоїU(x), .Приклад 1.

;

;

.

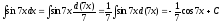I Метод заміни змінної в неозначеному інтегралі.

Якщо обчислюється 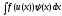, при цьому, тоді для спрощення при знаходженні відповіді такого інтеграла зручно ввести нову зміннуt=U(x), тоді

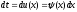
В новій змінній t наш інтеграл прийме вигляд .

Наприклад,.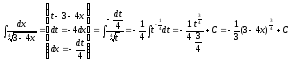

ІІ. Метод інтегрування частинами.

Основна формула цього метода 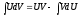, U=U(x), V=V(x) Даний метод стандартно використовується, якщо під знаком інтеграла є добуток степеневої функції на тригонометричну чи показникову, присутність під інтегралом логарифмічної або будь-якої оберненої тригонометричної функції, добуток позикової функції на тригонометричну. Також цей метод доцільний в деяких окремих випадках. За функцію U(x) звичайно приймають степеневу функцію (при диференціюванні степінь х понижується), логарифмічну чи обернену тригонометричну (оскільки для цих функцій відносно легко знаходяться похідні згідно відповідної таблиці). В ряді випадків даний метод застосовують послідовно декілька разів.

Приклад2.

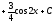
Корисним є обчислення інтеграла

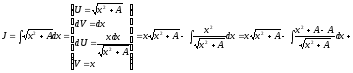
Звідки .

Аналогічно .

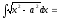
Два останні інтеграли самі по собі є корисними, наприклад, в геометричних додатках означеного інтеграла. З іншого боку цими формулами можливо користуватись як уже готовими.

Наприклад,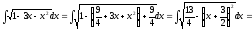

.

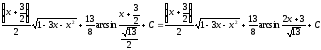ІІІ Метод інтегрування дробово-раціональних функцій.

Розглядається обчислення інтегралів вигляду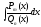, де,- многочлени відповідно зі степенемm і n змінної х. нагадаємо, що степінь многочлена встановлюється найбільшим показником степені х цього виразу. Якщо m<n, тоді дріб правильний, і його необхідно шляхом ділення многочлена чисельника на знаменник звести до суми многочлена результата ділення плюс уже правильний раціональний дріб. Згідно основної теореми алгебри многочлен 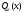завжди можливо записати у вигляді добутку лінійних нах множників типу, де k- кратність множника 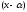, на квадратні тричлени типу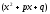з від’ємним дискримінантом, тобто<0. Згідно цього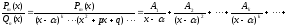

, де

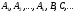
• деякі неозначені константи, для знаходження яких складають і розв’язують деяку алгебраїчну систему шляхом прирівнювання на основі рівності чисельників від коефіцієнтів при відповідно однакових степенях х. отримані після цього доданки інтегруються за допомогою інших методів інтегрування.

Приклад 3

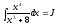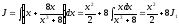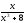. Оскільки m=4, n=3-дріб під інтегралом неправильний. Тому , тоді. Для обчисленнярозглянемо дрібна суму простіших дробів:, звідки

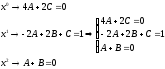
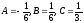
Отже, =.

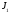Знайдемо первісну ;

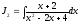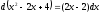,тоді .

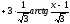Тоді первісна 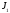може бути записана

. Остаточно відповідь початкового інтеграла 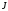буде.

ІV. Інтегрування ірраціональних функцій.

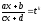Якщо обчислюється , тоді корисним є скористатись підстановкою виду, деk – спільний знаменник дробів .
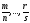