
- •9. Определенный интеграл и его приложения
- •9.1. Понятие определенного интеграла
- •Если предел последовательности интегральных сумм
- •9.2. Свойства определенного интеграла
- •9.4. Метод замены переменной в определенных интегралах
- •9.5. Метод интегрирования по частям в определенных интегралах
- •9.6. Вычисление площадей плоских фигур
- •9.7. Параметрические функции
- •9.8. Полярная система координат
- •9.9. Вычисление длины дуги плоской кривой
- •9.10. Вычисление площади поверхности вращения
- •9.11. Объем тела вращения
- •9.15. Несобственные интегралы
9.15. Несобственные интегралы
Несобственными интегралами называются 1) интегралы с бесконечными пределами (несобственные интегралы 1-го рода); 2) интегралы от неограниченных функций (несобственные интегралы 2-го рода).
Несобственный
интеграл от функции
![]() в пределах от
в пределах от![]() до
до![]() определяется равенством
определяется равенством
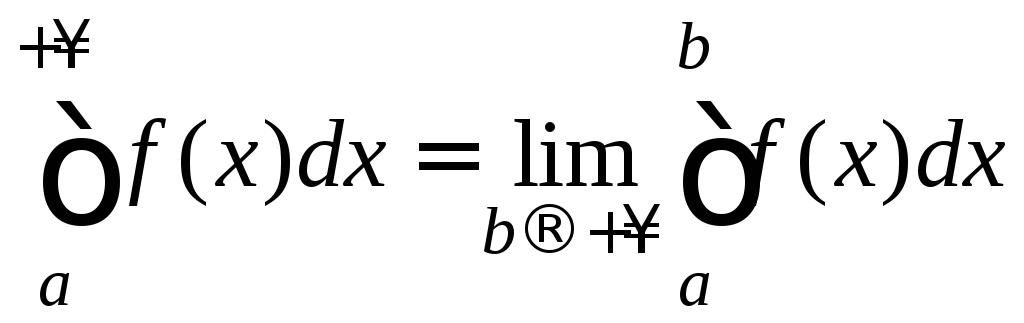 .
(9.35)
.
(9.35)
Если этот предел существует и конечен, то интеграл называется сходящимся, если же предел не существует или равен бесконечности, то интеграл называется расходящимся.
Аналогично определяются:
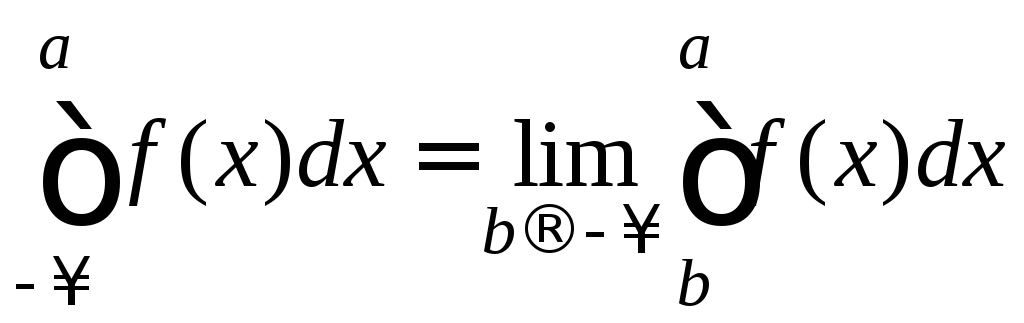 и
и
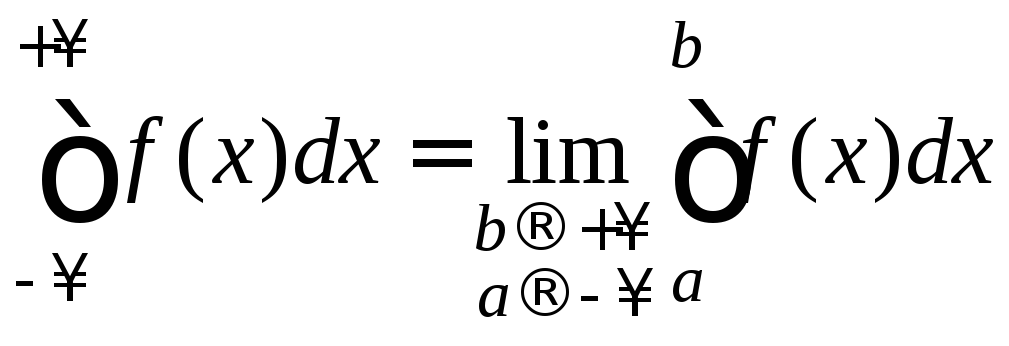 .
(9.36)
.
(9.36)
Если
функция имеет бесконечный разрыв в
точке
![]() отрезка
отрезка![]() и непрерывна при
и непрерывна при![]() и при
и при![]() ,
то несобственный интеграл 2-го рода
определяется следующим равенством:
,
то несобственный интеграл 2-го рода
определяется следующим равенством:
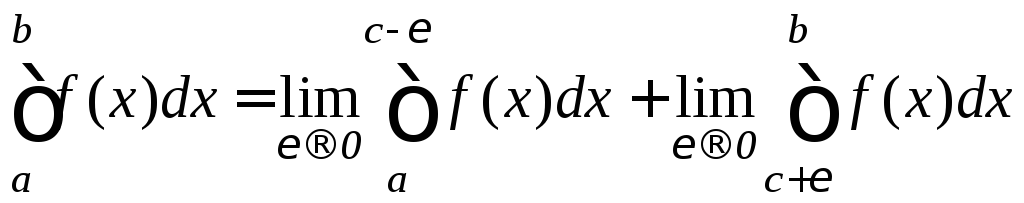 .
(9.37)
.
(9.37)
Несобственный интеграл 2-го рода называется сходящимся, если оба предела в правой части существуют и конечны; если же хотя бы один из интегралов не существует или бесконечен, то несобственный интеграл называется расходящимся.
Пример
19. Вычислить
несобственные интегралы (или установить
их расходимость): а)
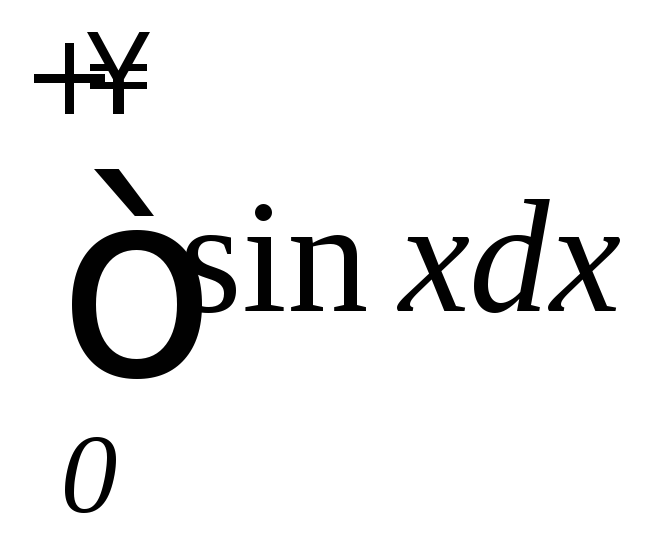 ;
б)
;
б)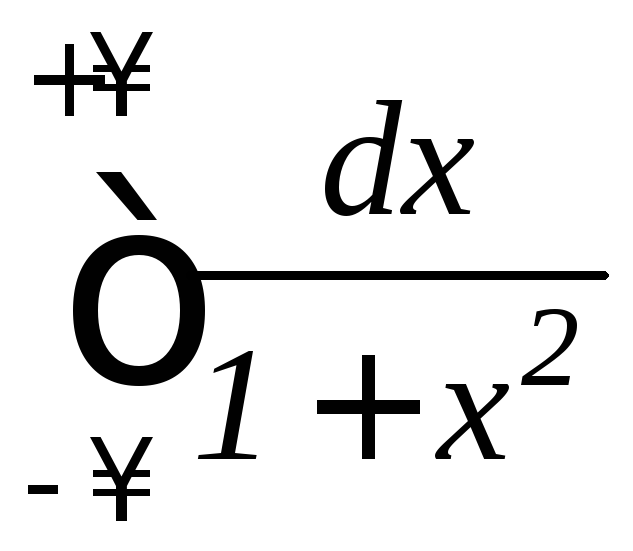 ;
в)
;
в)![]() .
.
Решение. а) Согласно формуле (9.35) получим
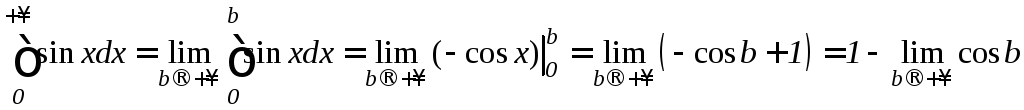 ,
,
т.е. предел не существует и несобственный интеграл расходится.
б) Используя четность подынтегральной функции и формулу (9.36), получим:
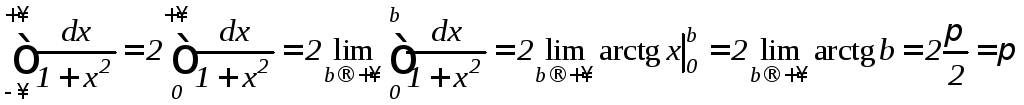 .
.
Следовательно,
несобственный интеграл сходится и равен
![]() .
.
в) Используя формулу (9.37), получим:
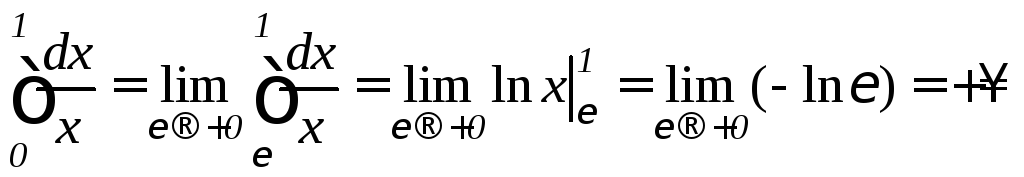 .
.
Следовательно, несобственный интеграл расходится.
Задание 9.1. Вычислить определенные интегралы:
|
1.
а)
|
б)
|
в)
|
|
2.
а)
|
б)
|
в)
|
|
3.
а)
|
б)
|
в)
|
|
4.
а)
|
б)
|
в)
|
|
5.
а)
|
б)
|
в)
|
|
6.
а)
|
б)
|
в)
|
|
7.
а)
|
б)
|
в)
|
|
8.
а)
|
б)
|
в)
|
|
9.
а)
|
б)
|
в)
|
|
10.
а)
|
б)
|
в)
|
|
11.
а)
|
б)
|
в)
|
|
12.
а)
|
б)
|
в)
|
|
13.
а)
|
б)
|
в)
|
|
14.
а)
|
б)
|
в)
|
|
15.
а)
|
б)
|
в)
|
|
16.
а)
|
б)
|
в)
|
|
17.
а)
|
б)
|
в)
|
|
18.
а)
|
б)
|
в)
|
|
19.
а)
|
б)
|
в)
|
|
20.
а)
|
б)
|
в)
|
|
21.
а)
|
б)
|
в)
|
|
22.
а)
|
б)
|
в)
|
|
23.
а)
|
б)
|
в)
|
|
24.
а)
|
б)
|
в)
|
|
25.
а)
|
б)
|
в)
|
Задание 9.2. Найти площадь фигуры, ограниченной заданными линиями:
|
1. x = acos3t, y = asin3t; |
14. y2 = x, y = x2; | |
|
2. y = lnx, 2 x 5; |
15. y = –x2+2x+3, y = x2–4x+3; | |
|
3. = acos3, (a>0); |
16. x = 6(t–sint), y = 6(1–cost) (y9); | |
|
4. xy = 4, x=1, x=4, y=0; |
17. y = arсcos x, x = 0, y = 0; | |
|
5. xy = 4, x+y–5=0; |
18.
| |
|
6. = cos2; |
19. y2 = 2x, y2 = –x2+4x; | |
|
7. y2 = 16–8x, y2 = 24x+48; |
20.
| |
|
8. = sin3; |
21.
| |
|
9. y = x2–3x, 3x+y–4=0, x=0; |
22.
| |
|
10. = 6cos3, = 3 (3); |
23.
| |
|
11. x = tg3x, y = 0, x = /12; |
24.
| |
|
12. = 2cos6; |
25.
| |
|
13.
|
| |
Задание 9.3. Найти длину кривой:
|
1.
|
14.
|
|
2. x = 5(t–sint), y = 5(1–cost) при 0 x ; |
15.
|
|
3. 9y2 = x(3–x)2, между точками пересечения кривой с осью Ox; |
16.
|
|
4.
|
17.
|
|
5.
|
18.
|
|
6.
|
19. |
|
7.
|
20.
|
|
8.
|
21.
|
|
9.
|
22.
|
|
10.
|
23.
|
|
11. |
24.
|
|
12.
|
25.
|
|
13.
|
|
Задание 9.4. Определить объем тела, образованного вращением вокруг указанной оси плоской фигуры, ограниченной заданными линиями:
|
1.
|
|
2.
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
|
7.
|
|
8.
|
|
9.
|
|
10.
|
|
11.
|
|
12.
|
|
13.
|
|
14.
|
|
15.
|
|
16.
|
|
17.
|
|
18.
|
|
19.
|
|
20.
|
|
21.
|
|
22.
|
|
23.
|
|
24.
|
|
25.
|
Задание 9.5. Вычислить площадь поверхности, образованной вращением линии:
|
1.
|
|
2.
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
|
7.
|
|
8.
|
|
9.
|
|
10.
|
|
11.
|
|
12.
|
|
13.
|
|
14.
|
|
15.
|
|
16.
|
|
17.
|
|
18.
|
|
19.
|
|
20.
|
|
21.
|
|
22.
|
|
23.
|
|
24.
|
|
25.
|
Задание 9.6. Вычислить работу, которую необходимо затратить, чтобы выкачать жидкость удельного веса из резервуара, имеющего форму
а) конуса вращения, обращенного вершиной вниз, высота которого H, а радиус основания R:
|
1. H = 6 м, R = 4 м; |
6. H = 3 м, R = 7 м; |
|
2. H = 2 м, R = 3 м; |
7. H = 3 м, R = 4 м; |
|
3. H = 8 м, R = 3 м; |
8. H = 4 м, R = 5 м; |
|
4. H = 2 м, R = 5 м; |
9. H = 5 м, R = 6 м. |
|
5. H = 6 м, R = 5 м; |
|
б) полусферы, обращенной выпуклостью вниз, радиус основания которой равен R:
|
10. R = 10 м; |
14. R = 15 м; |
|
11. R = 20 м; |
15. R = 6 м; |
|
12. R = 30 м; |
16. R = 7 м. |
|
13. R = 4 м; |
17. R = 8 м. |
в) форму цилиндра высоты H и радиуса основания R:
|
18. H = 5 м, R = 2 м; |
22. H = 3 м, R = 2 м; |
|
19. H = 4 м, R = 3 м; |
23. H = 3 м, R = 5 м; |
|
20. H = 5 м, R = 3 м; |
24. H = 7 м, R = 2 м; |
|
21. H = 6 м, R = 3 м; |
25. H = 2 м, R = 4 м; |
Задание 9.7. Вычислить несобственные интегралы или установить их расходимость:
|
1.
а)
|
14.
а)
|
|
2.
а)
|
15.
а)
|
|
3.
а)
|
16.
а)
|
|
4.
а)
|
17.
а)
б)
|
|
5.
а)
|
18.
а)
|
|
6.
а)
|
19.
а)
|
|
7.
а)
|
20.
а)
|
|
8.
а)
|
21.
а)
|
|
9.
а)
|
22.
а)
|
|
10.
а)
|
23.
а)
|
|
11.
а)
б)
|
24.
а)
б)
|
|
12.
а)
б)
|
25.
а)
б)
|
|
13.
а)
|
|

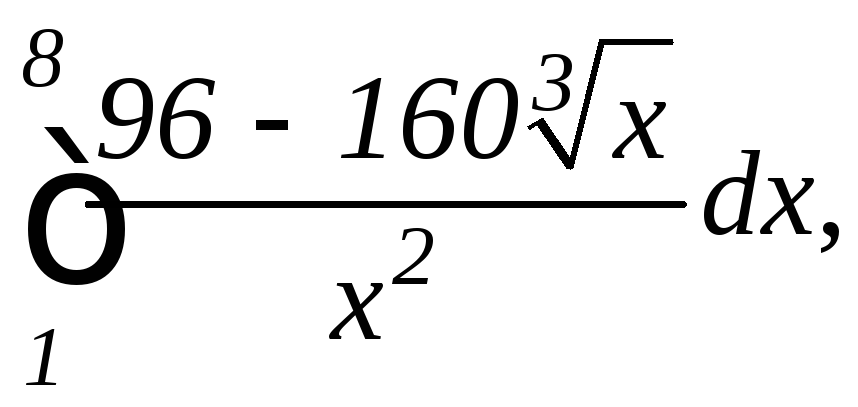
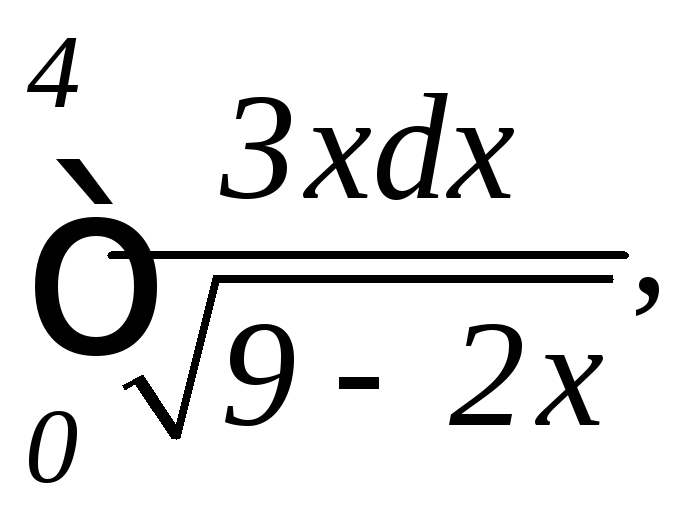
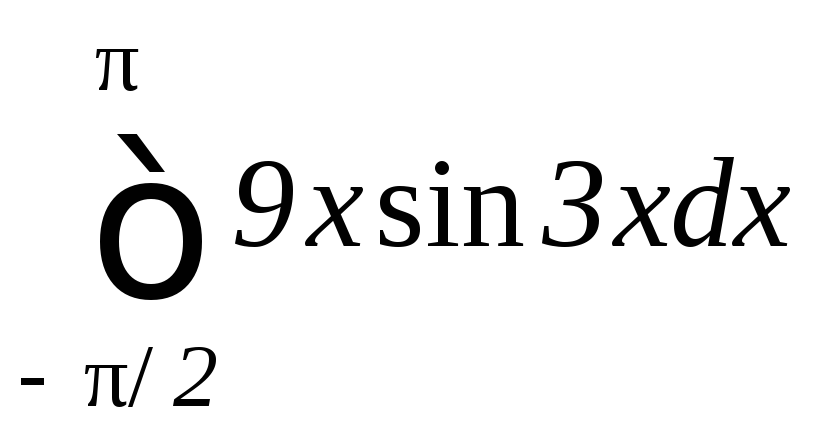 .
.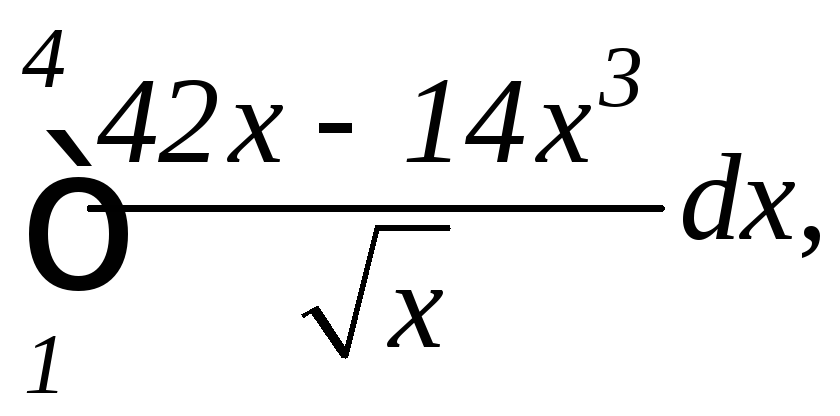
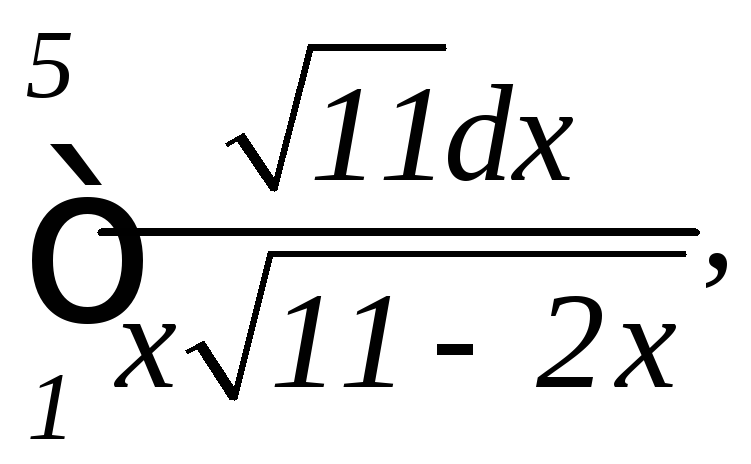
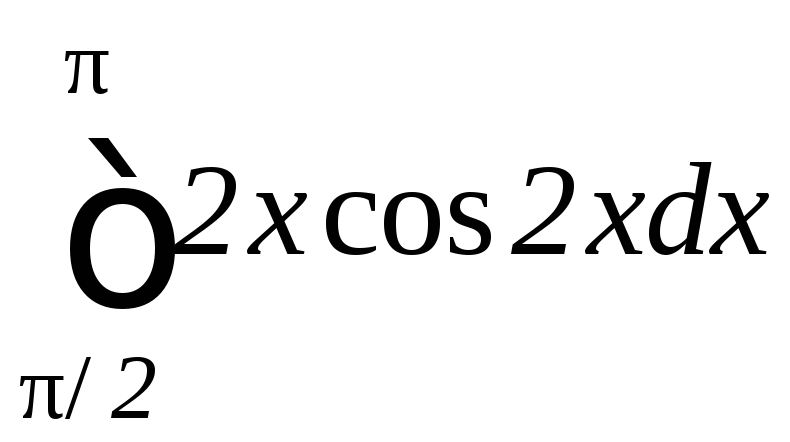 .
.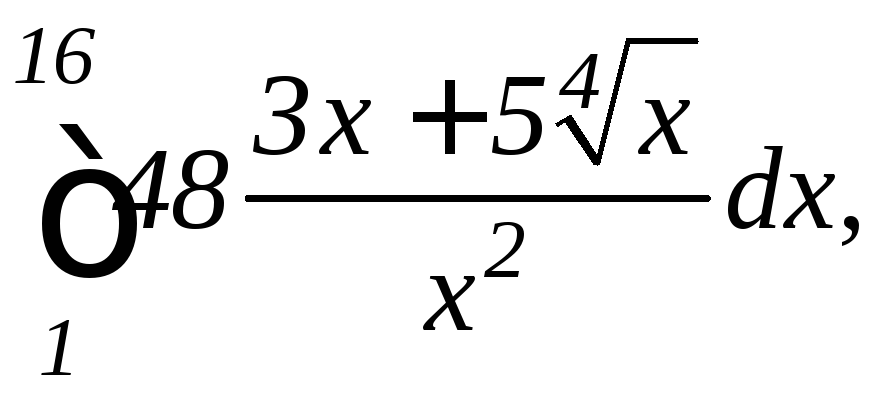
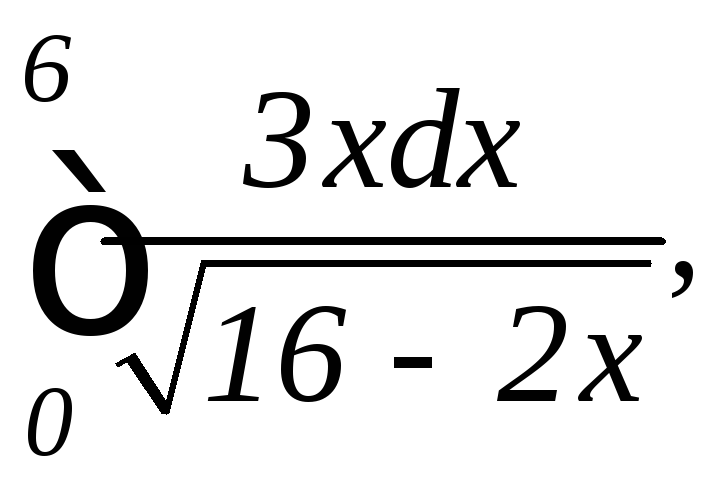
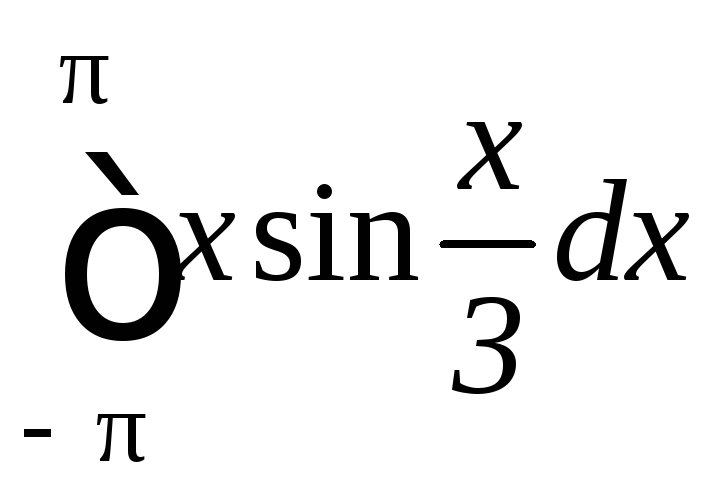 .
.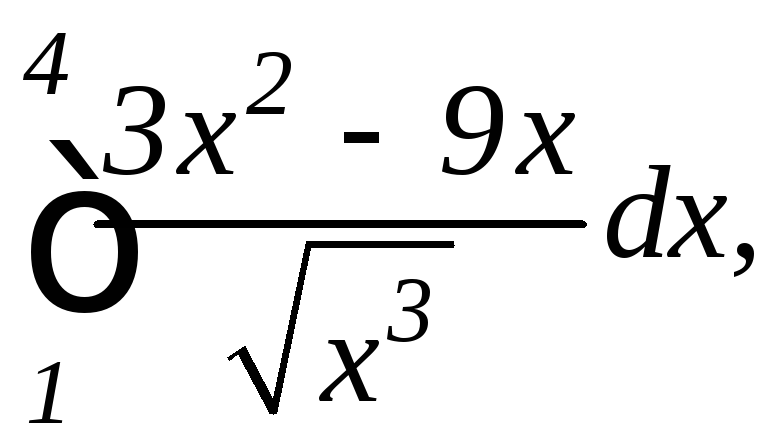
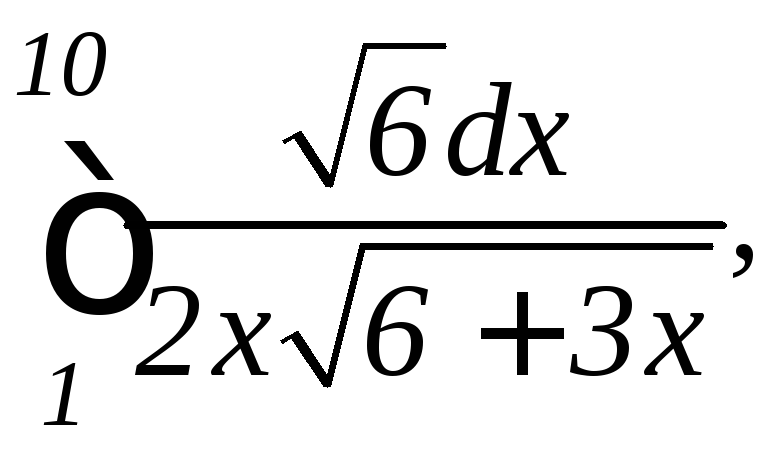
 .
.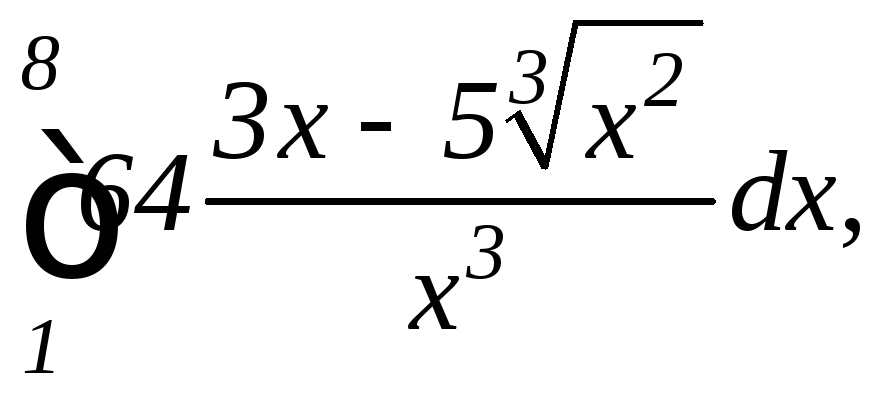
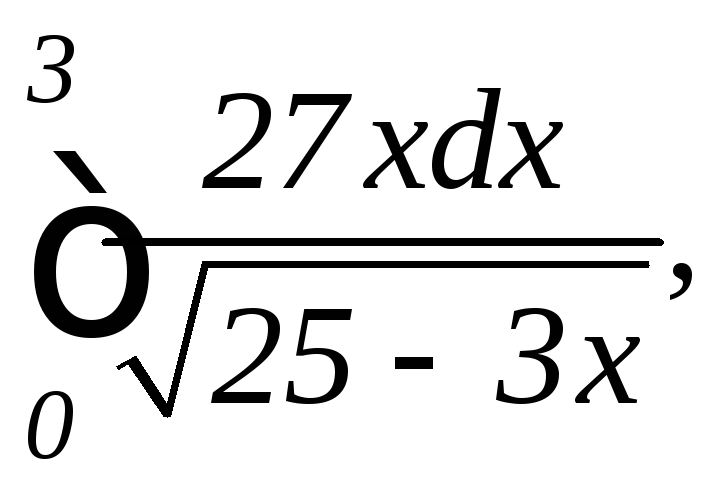
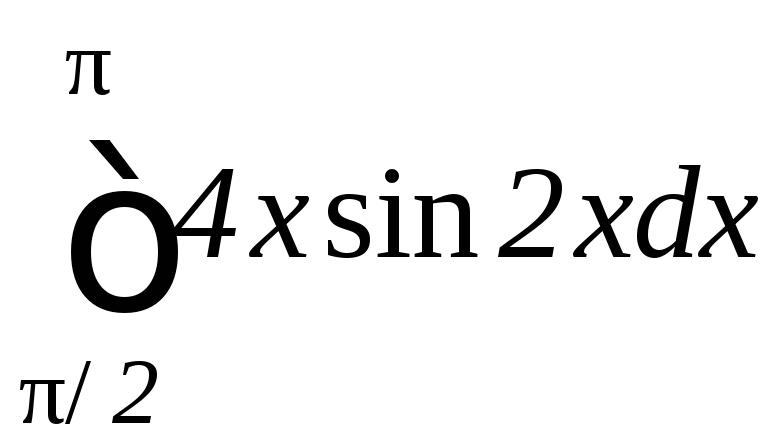 .
.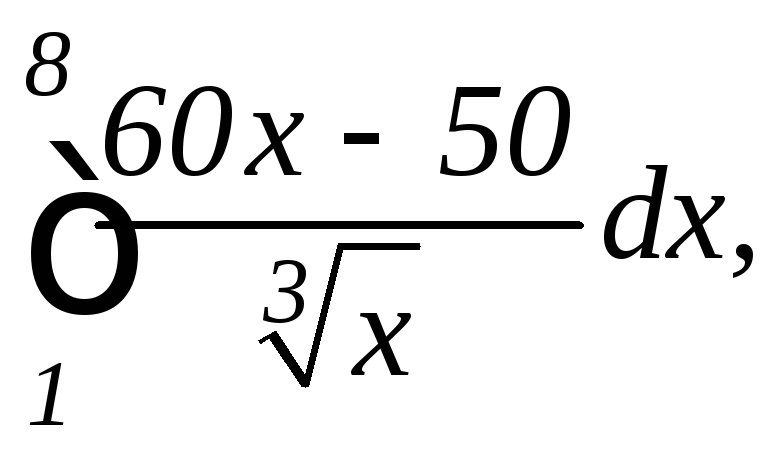
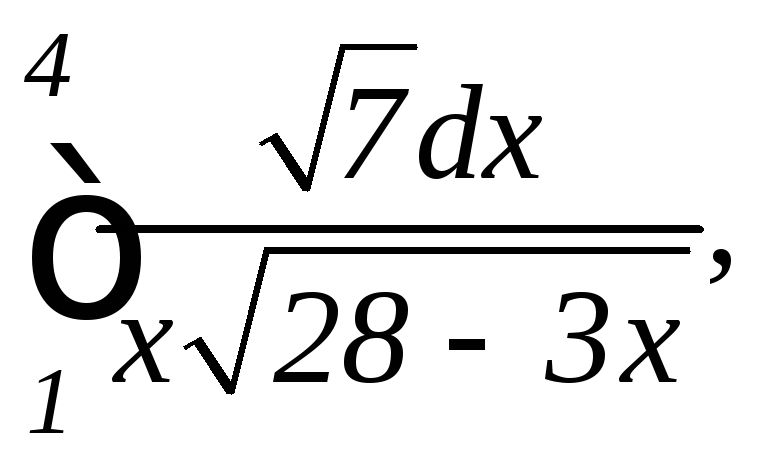
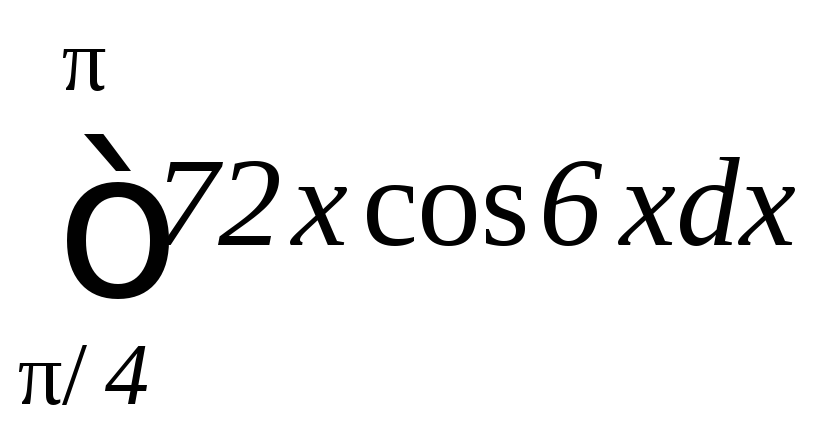 .
.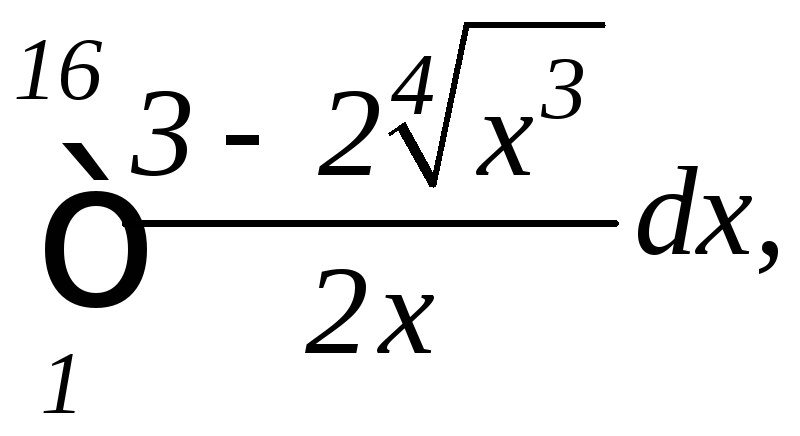
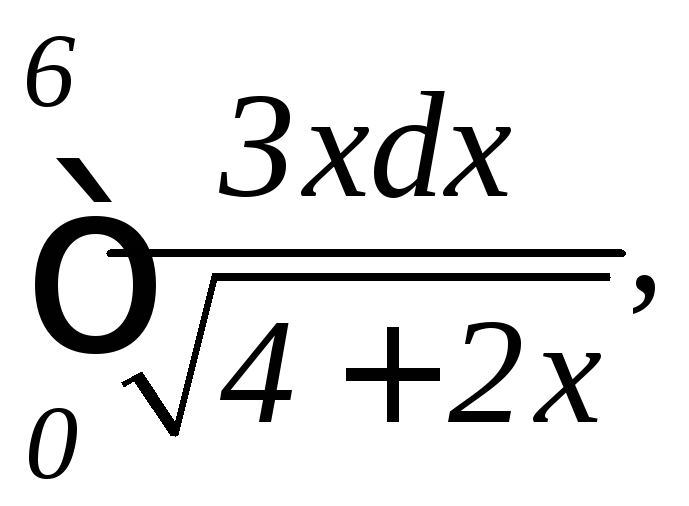
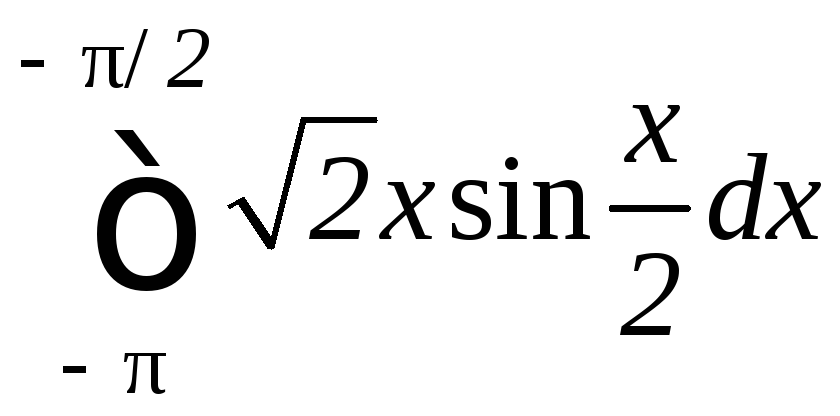 .
.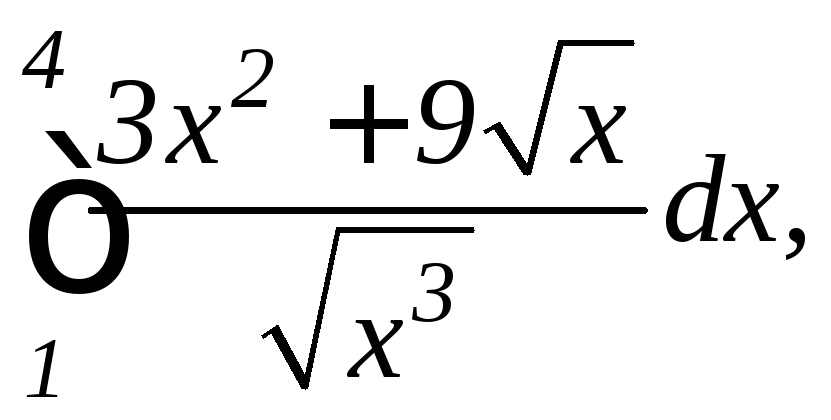
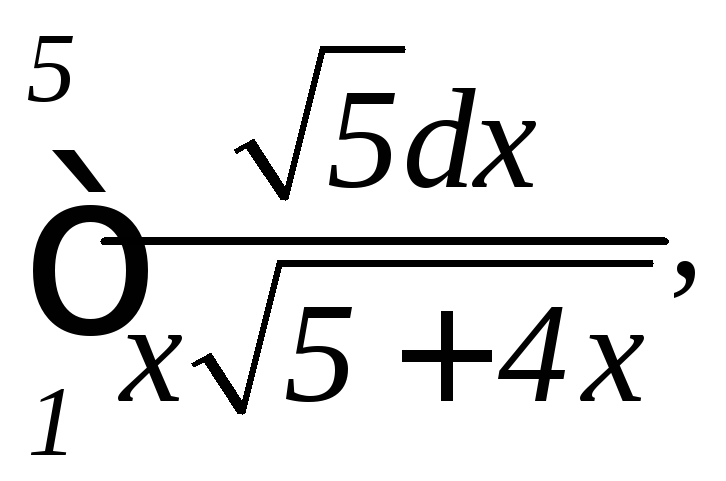
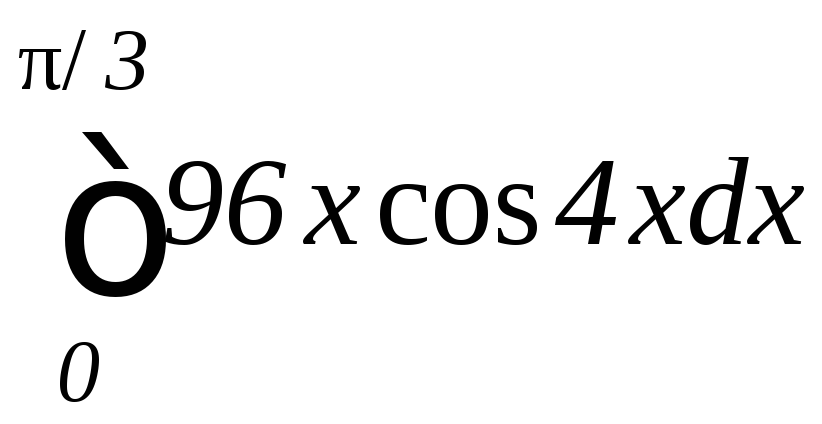 .
.
 .
.
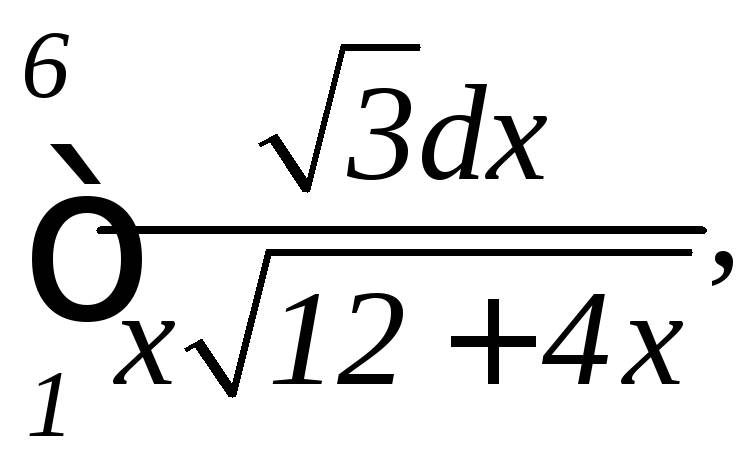
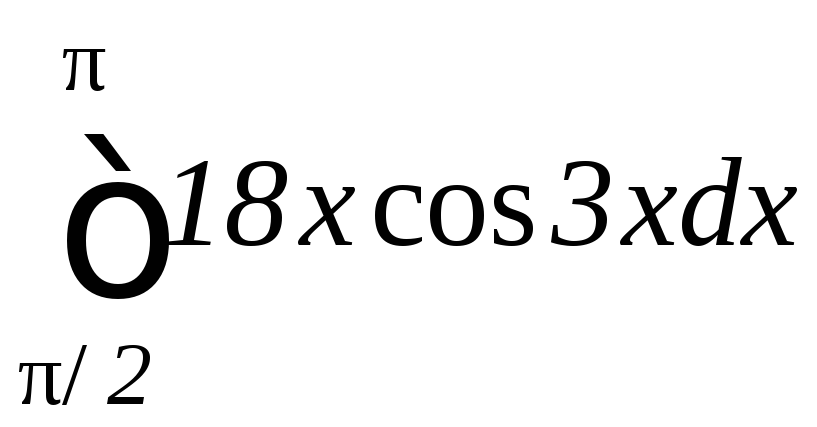 .
.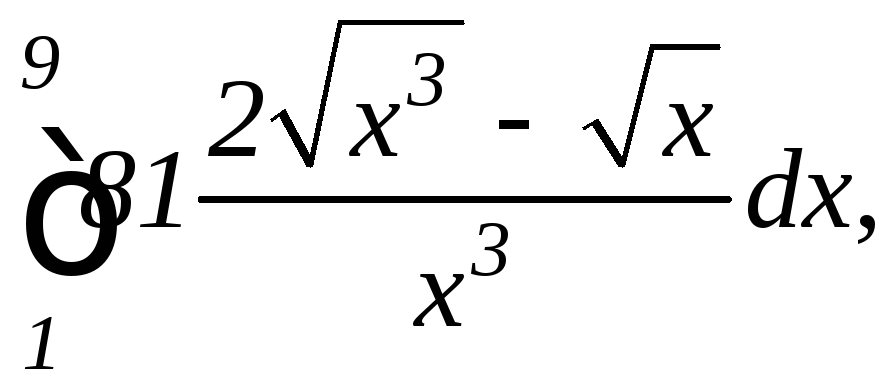

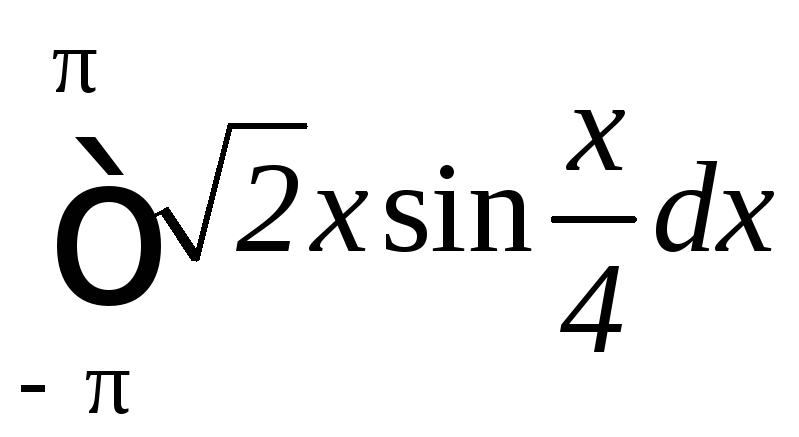 .
.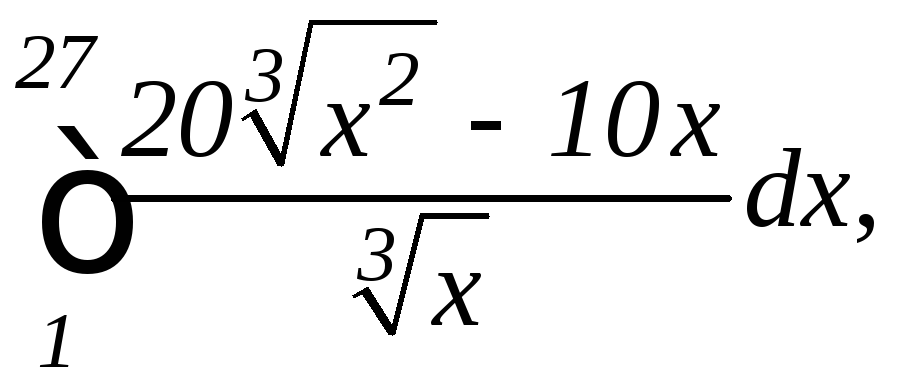
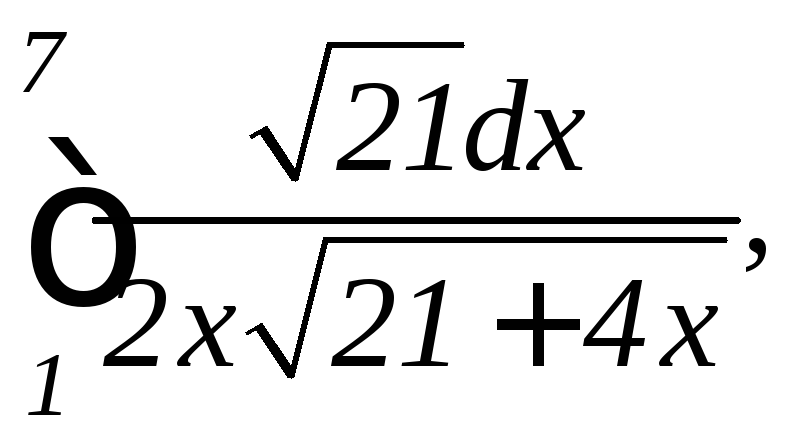
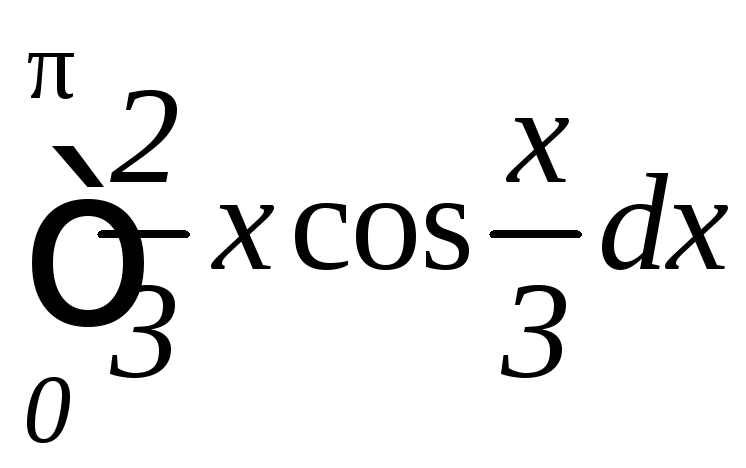 .
.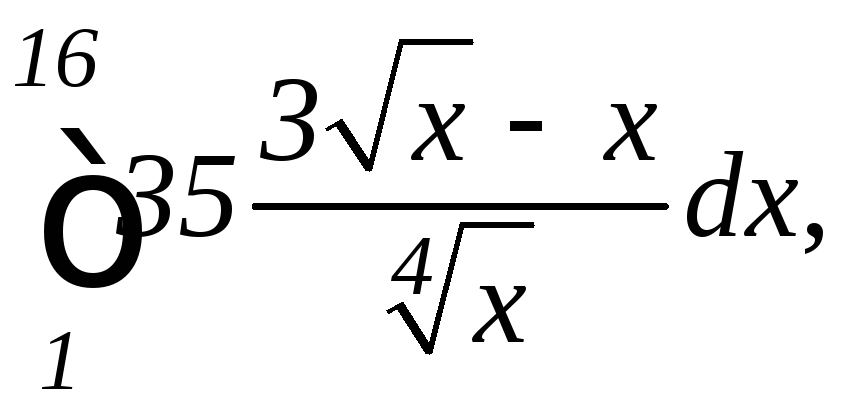
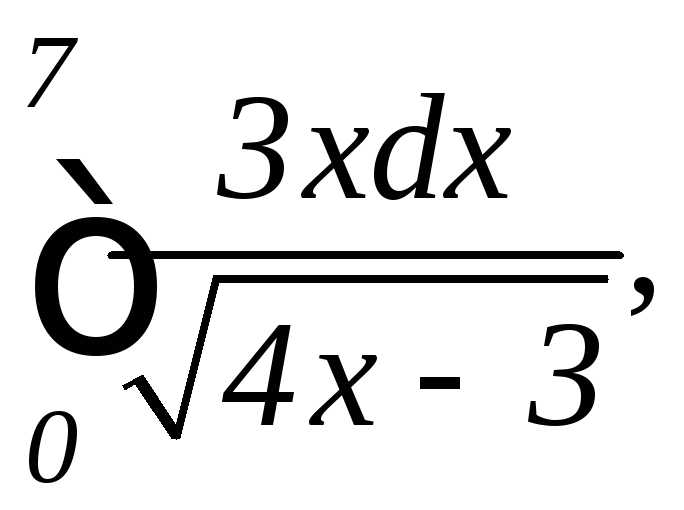
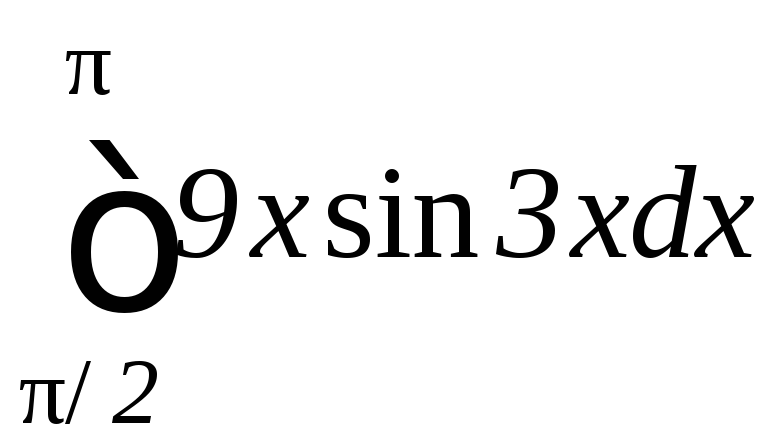 .
.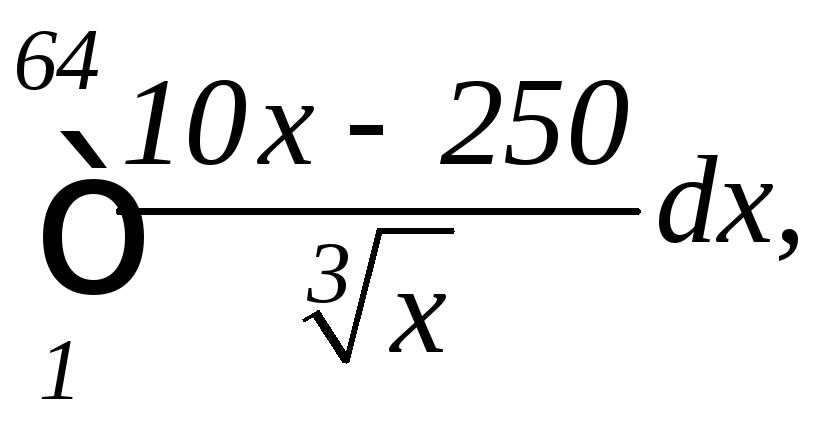
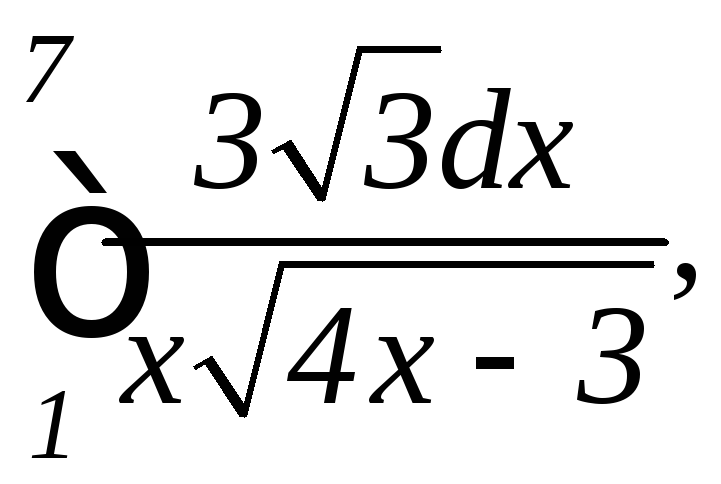
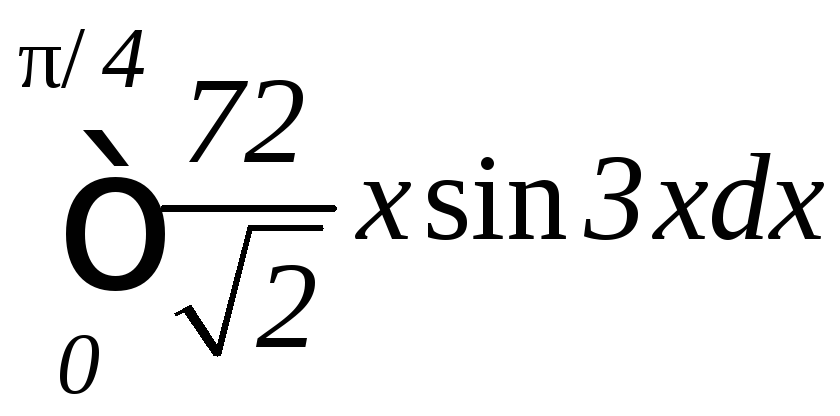 .
.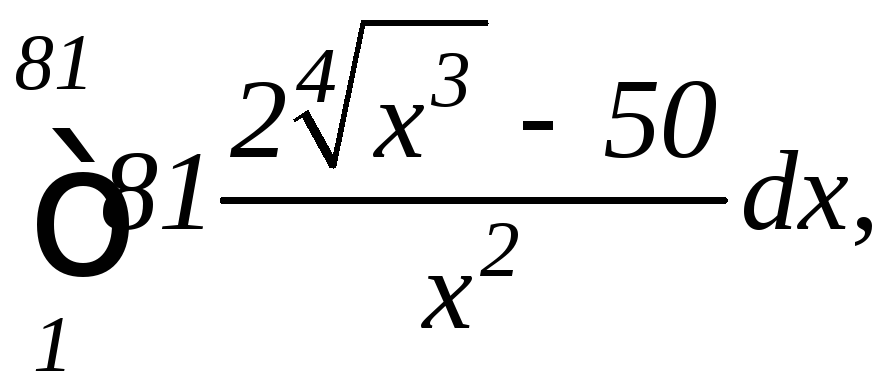
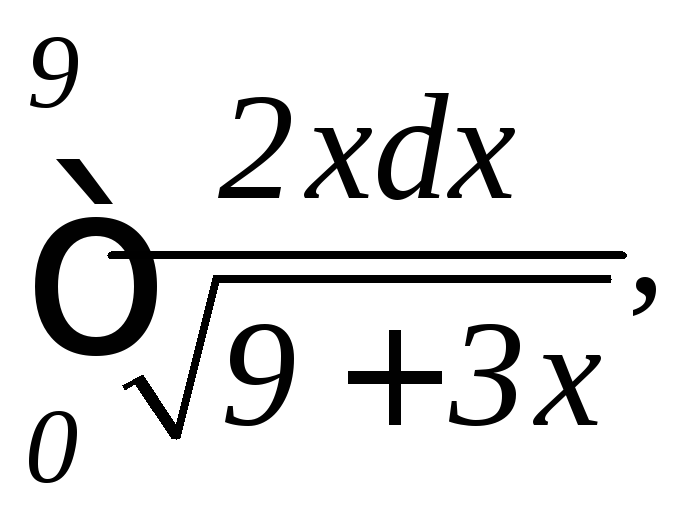
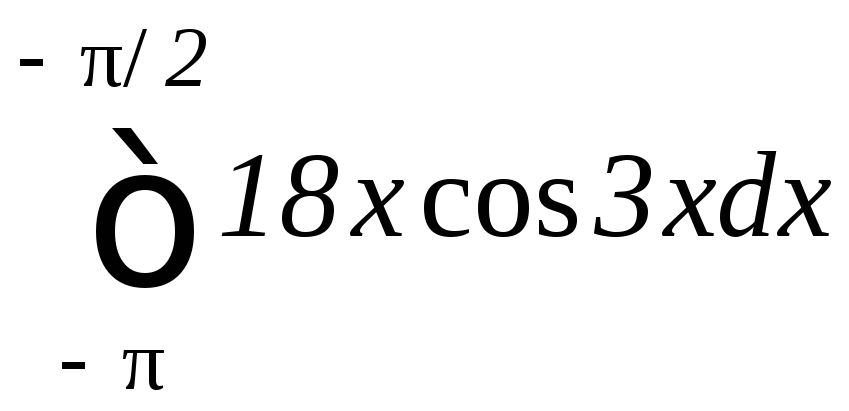 .
.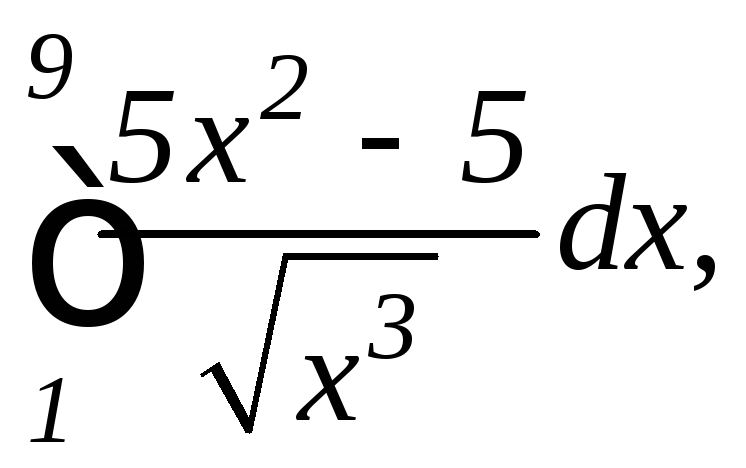
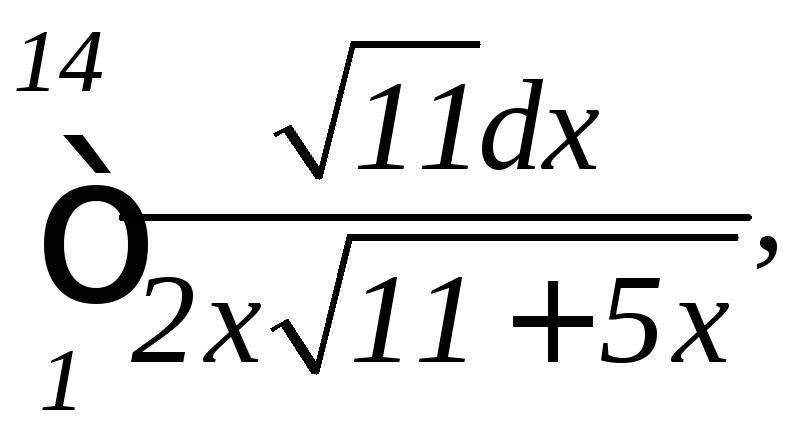
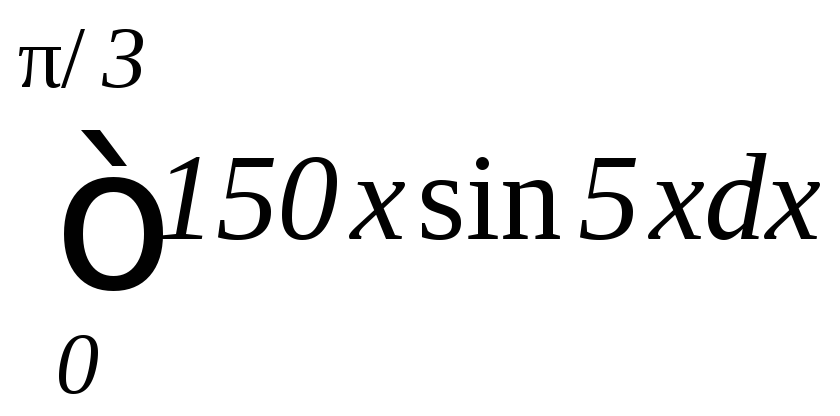 .
.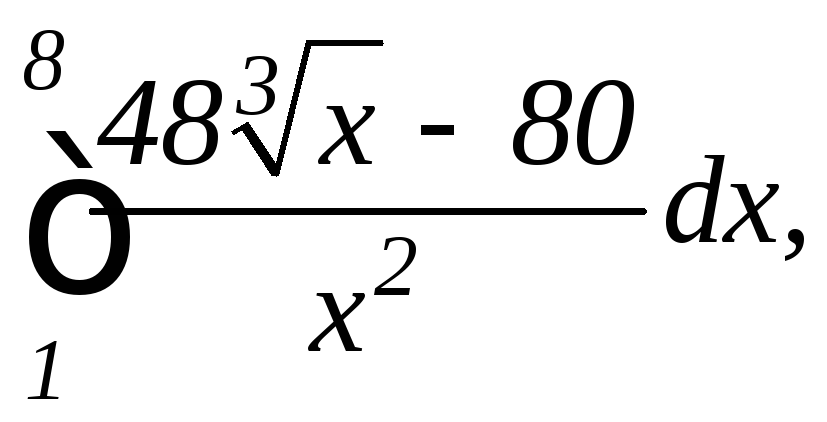
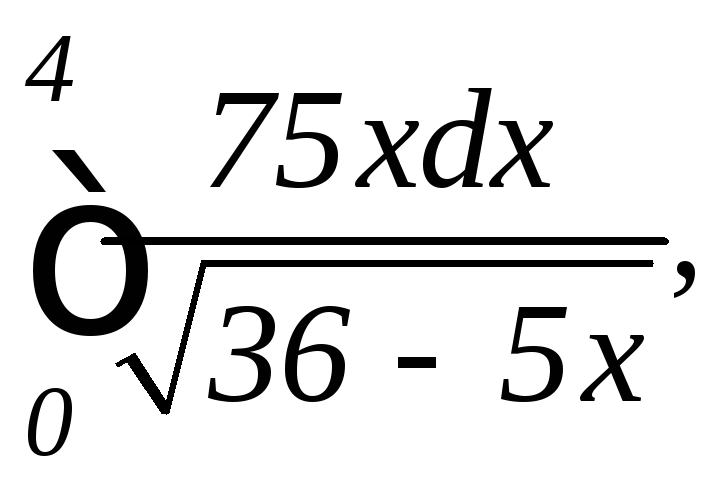
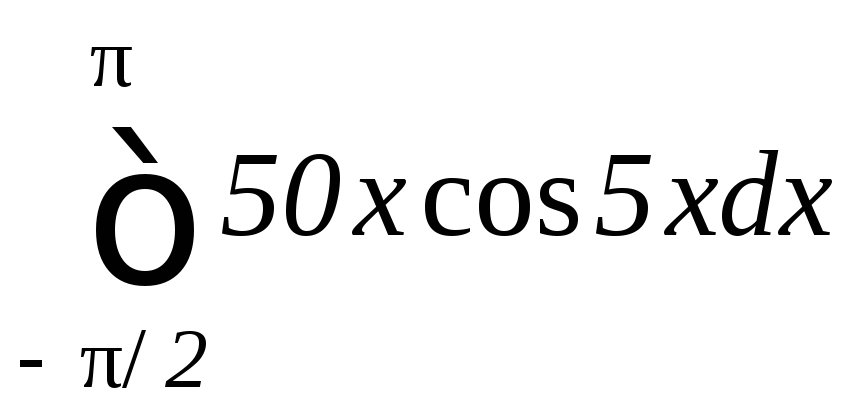 .
.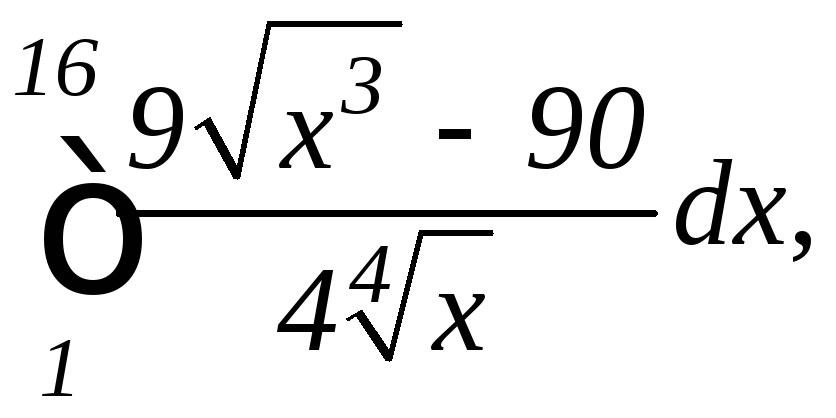

 .
.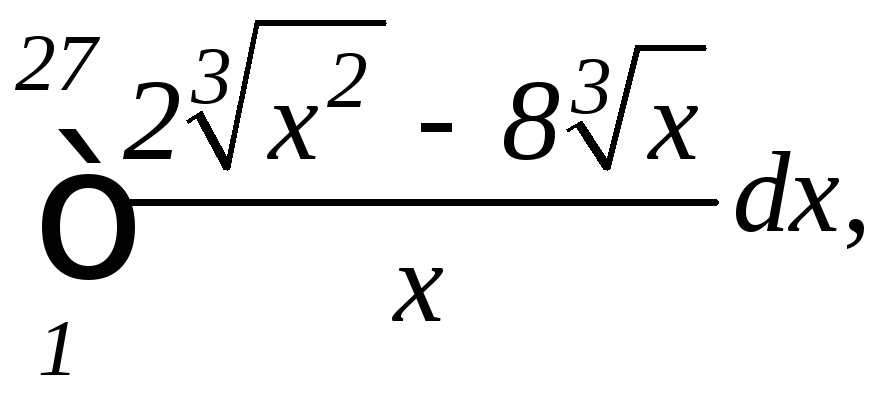
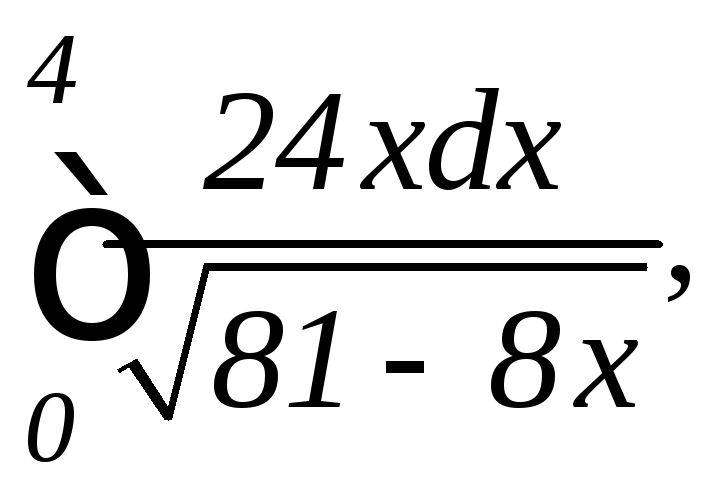
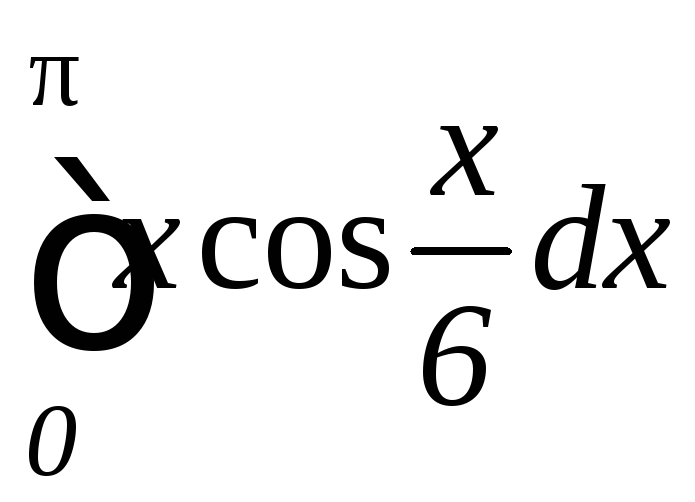 .
.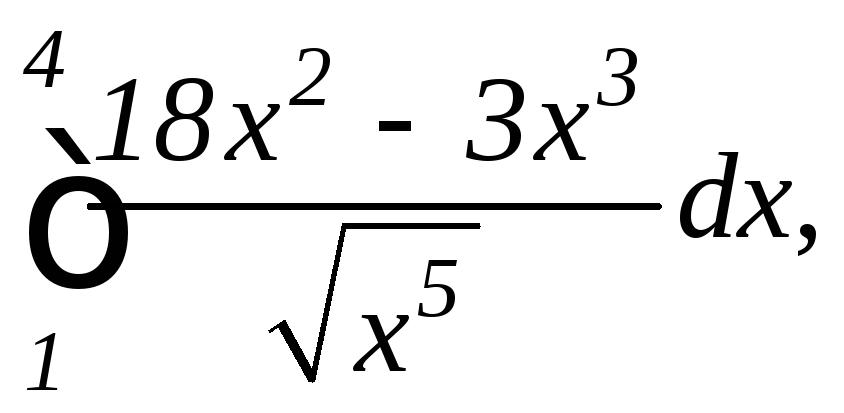
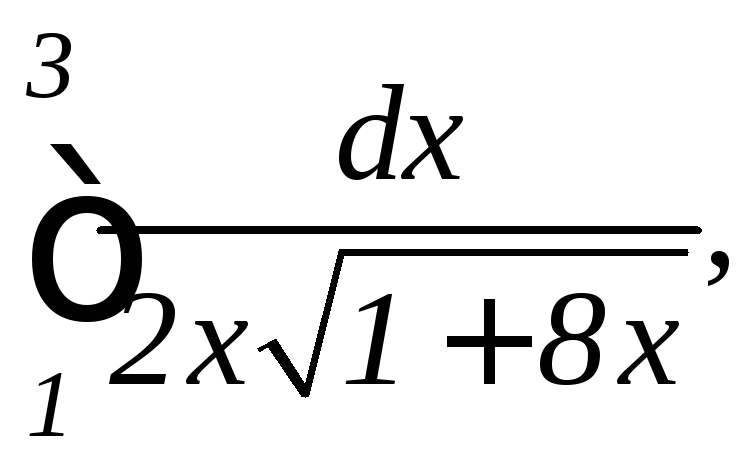
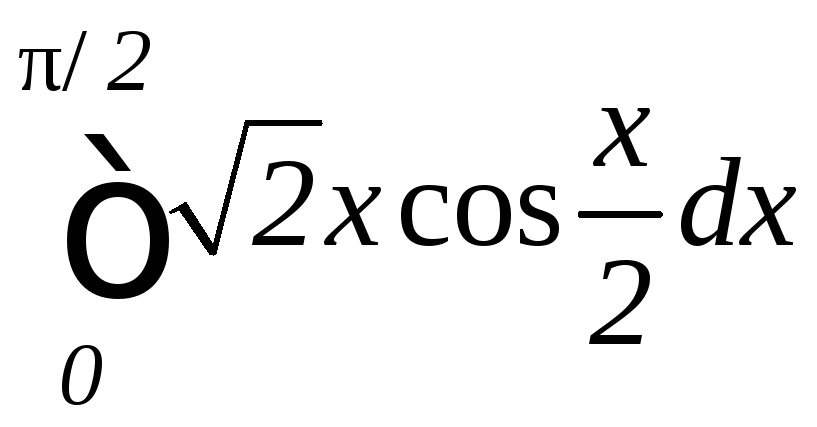 .
.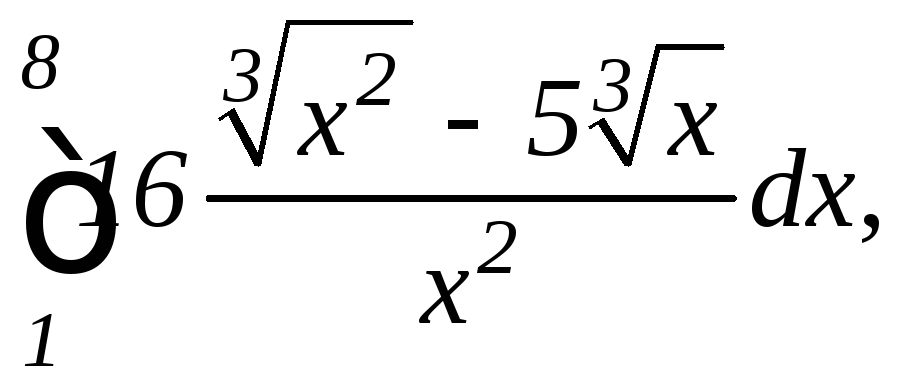
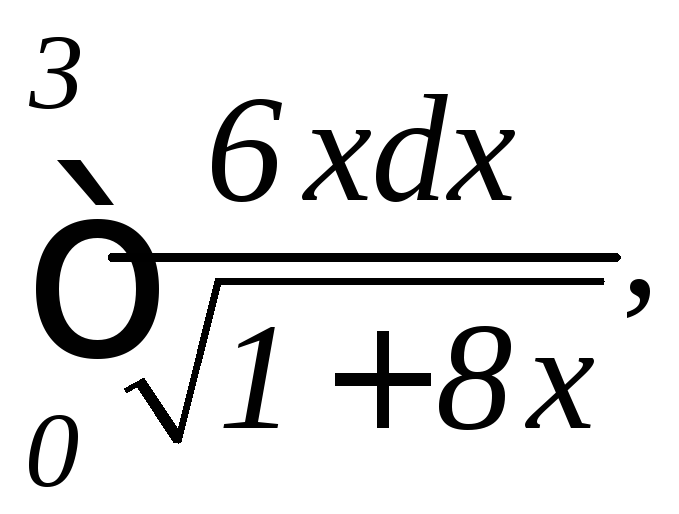
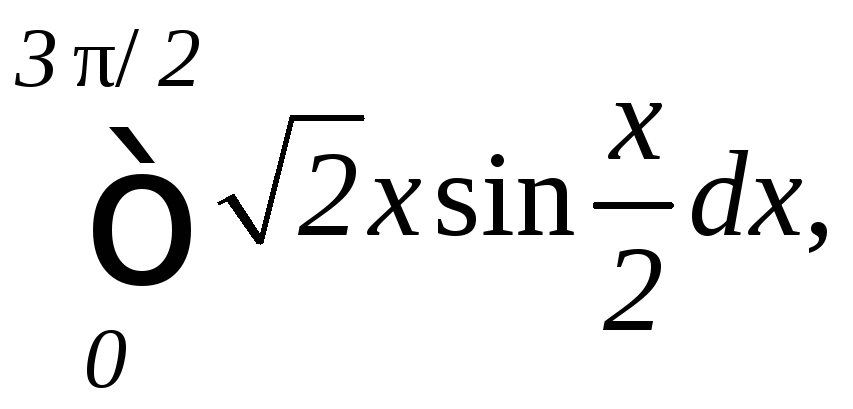 .
.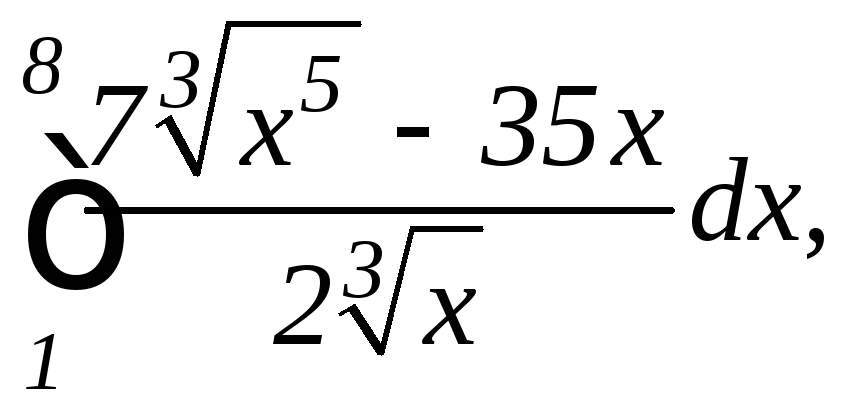
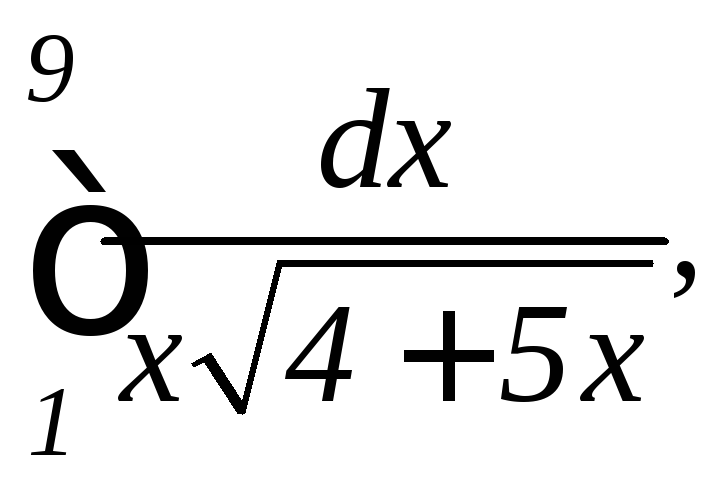
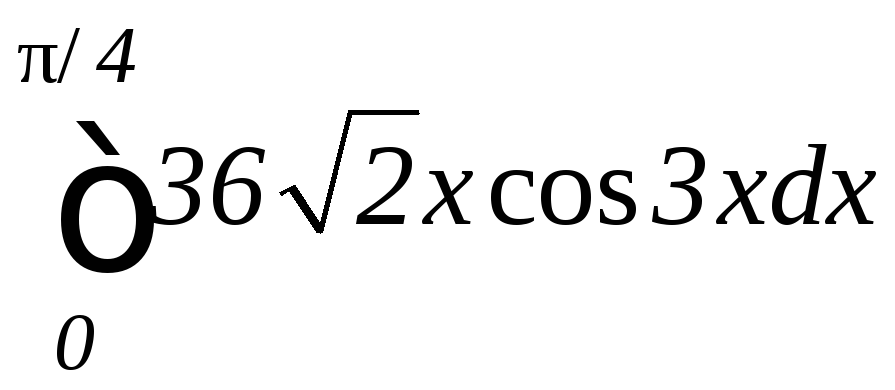 .
.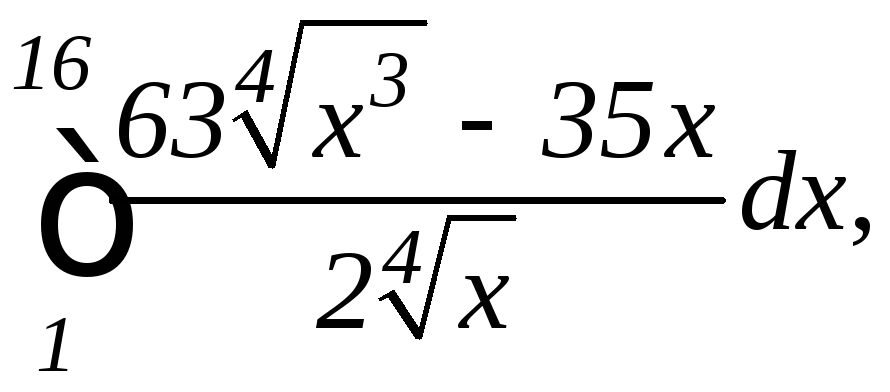
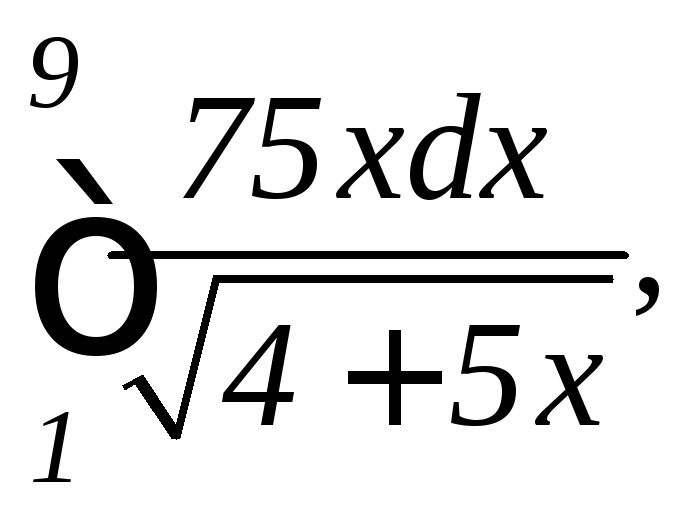
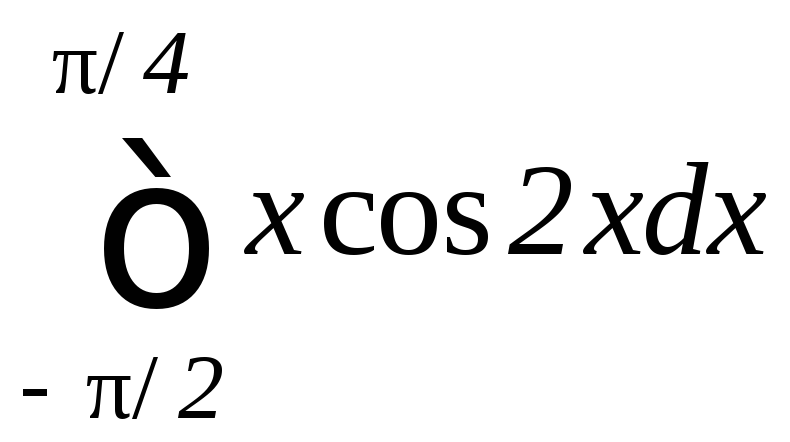 .
.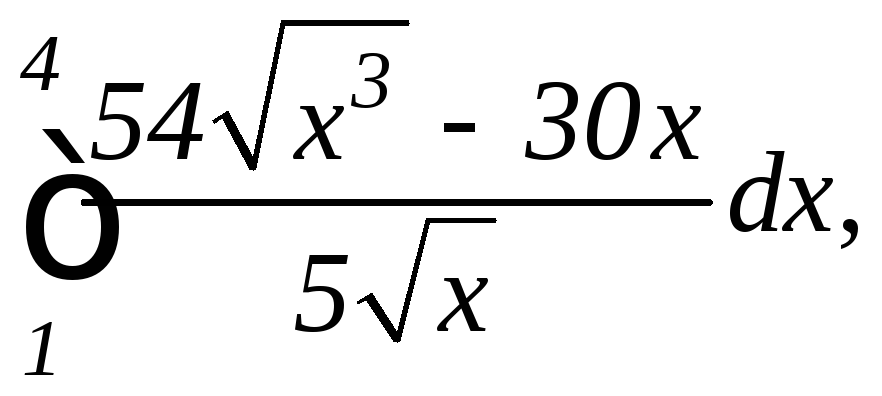
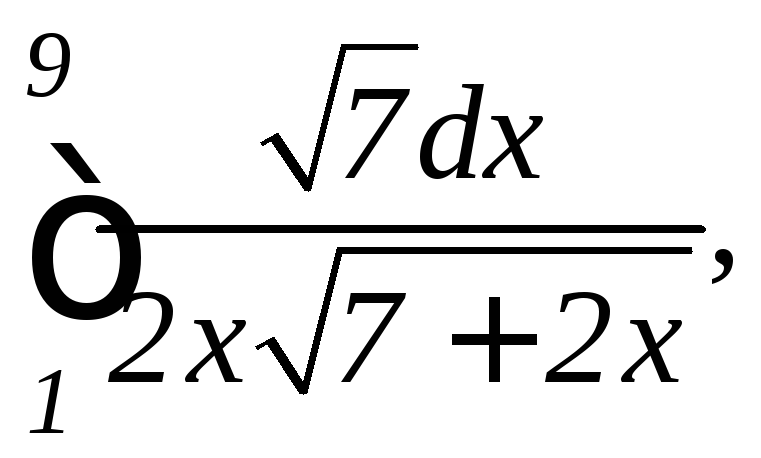
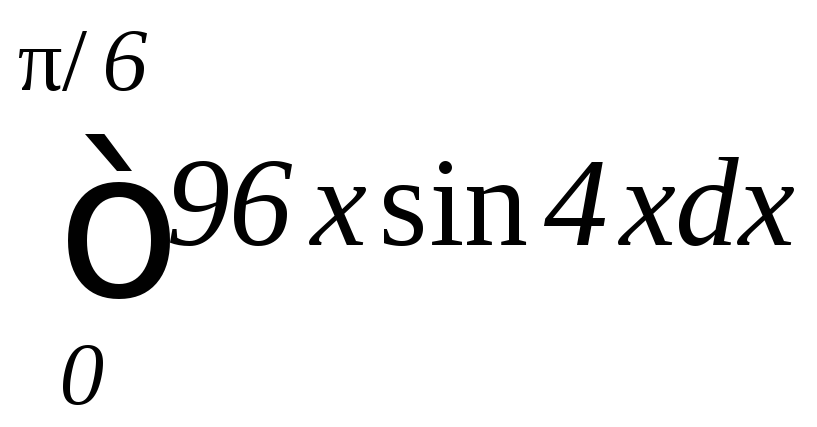 .
.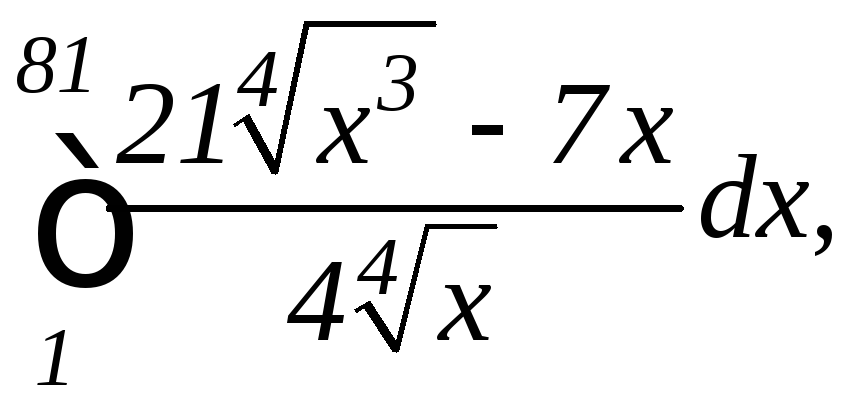
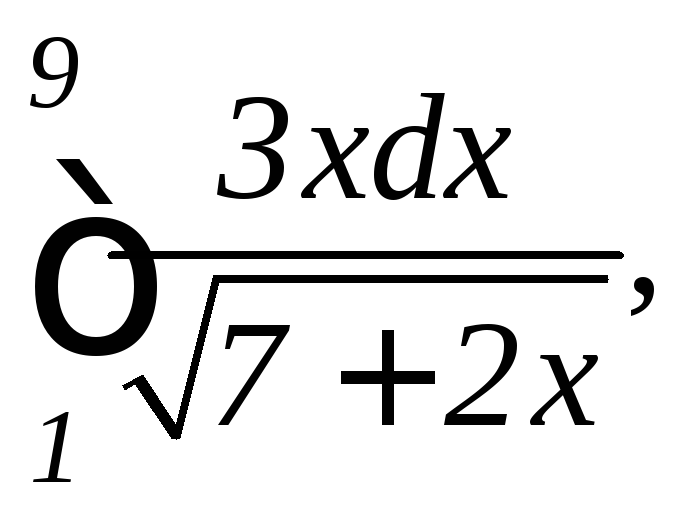
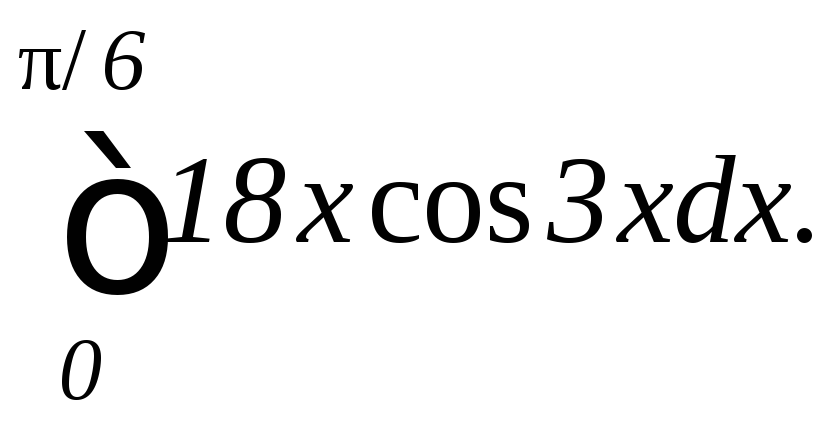
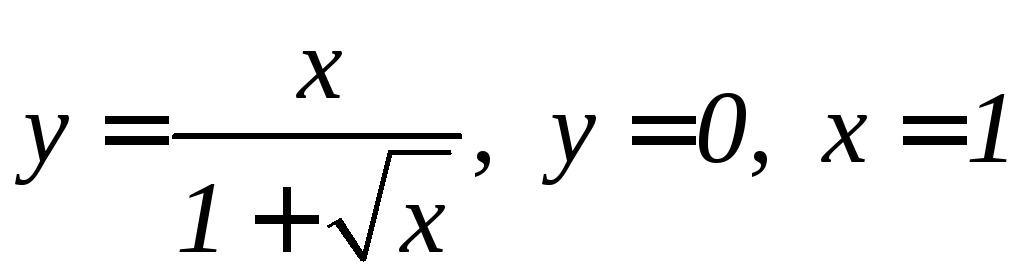 ;
;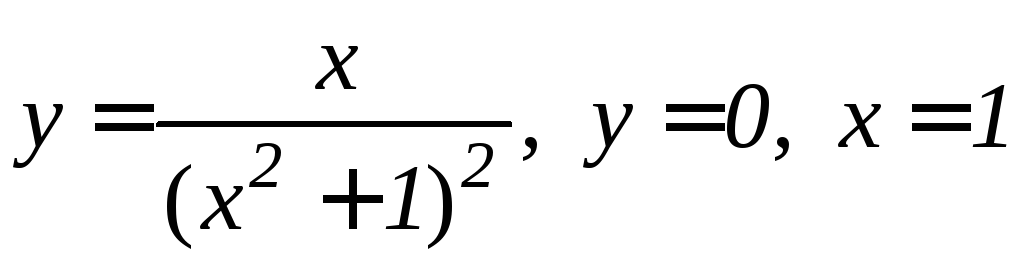 .
.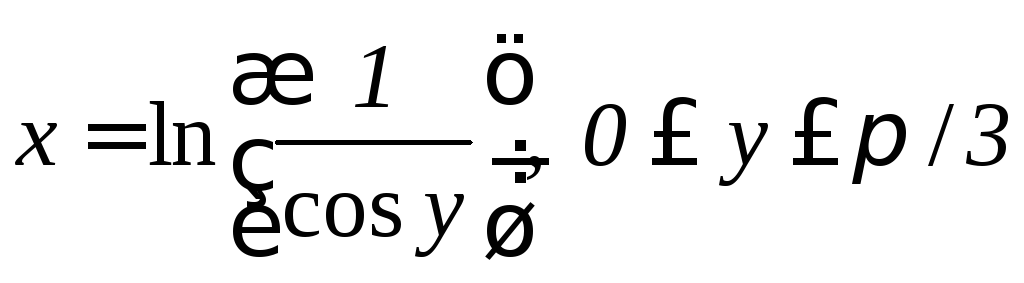 ;
;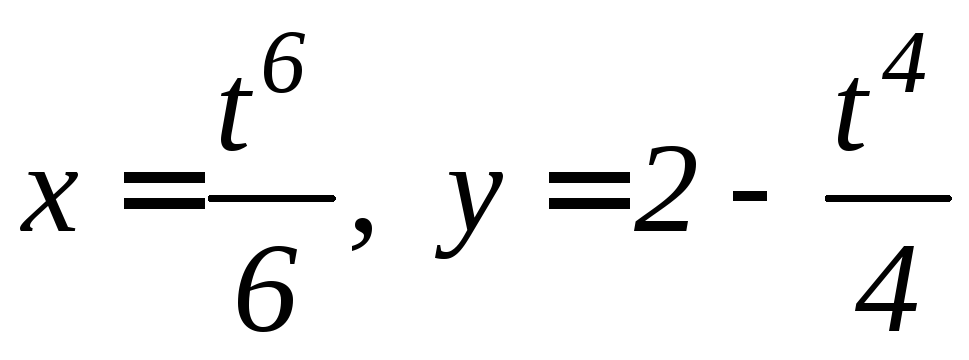 ,
между точками пересечения линии с
осями координат;
,
между точками пересечения линии с
осями координат;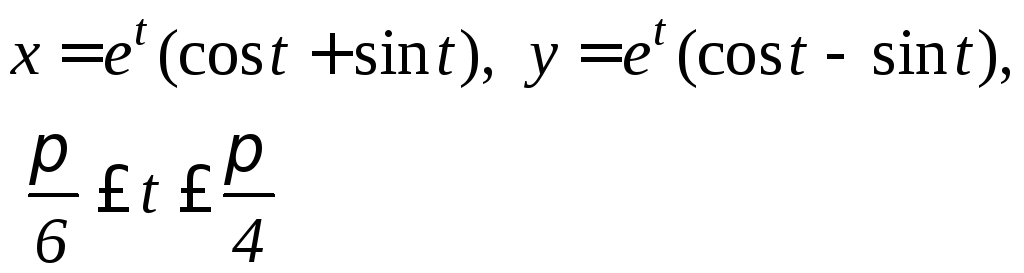
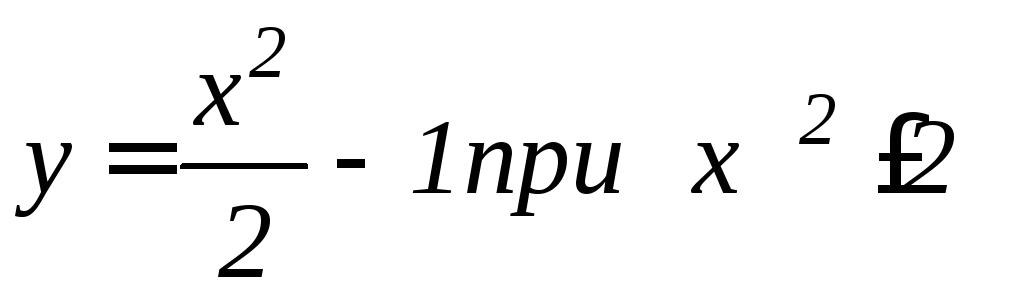 ;
;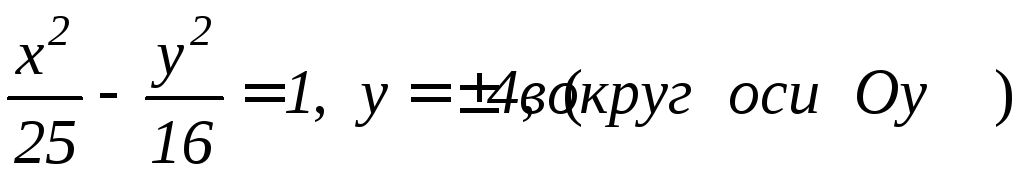 ;
;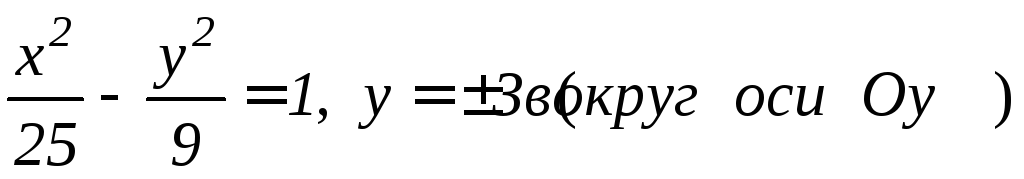 ;
;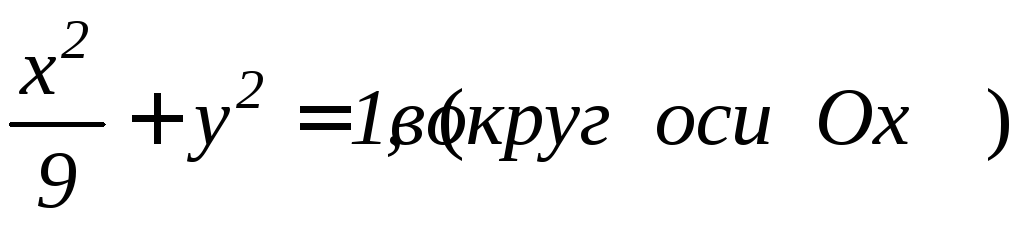 ;
;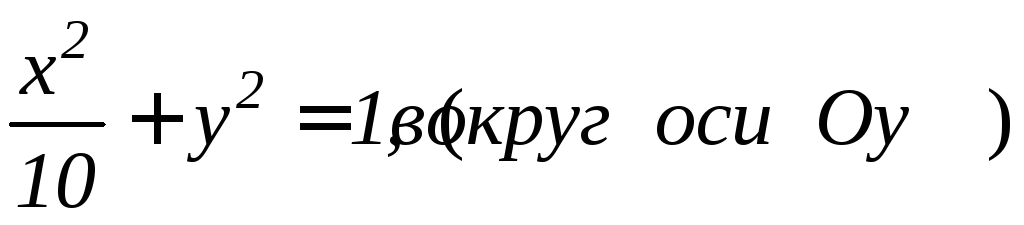 ;
;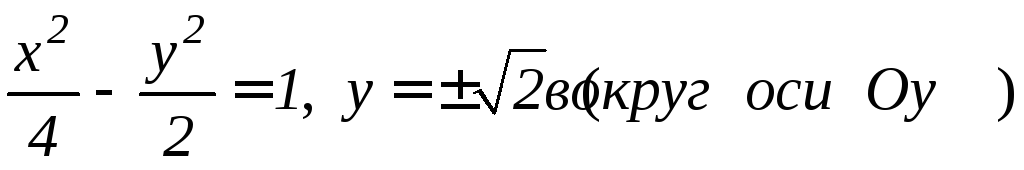 ;
;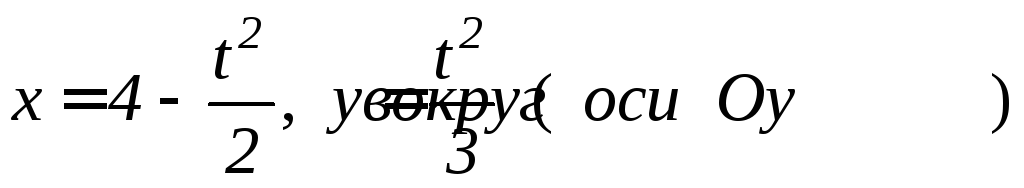 ,
между точками пересечения линии с
осями координат;
,
между точками пересечения линии с
осями координат;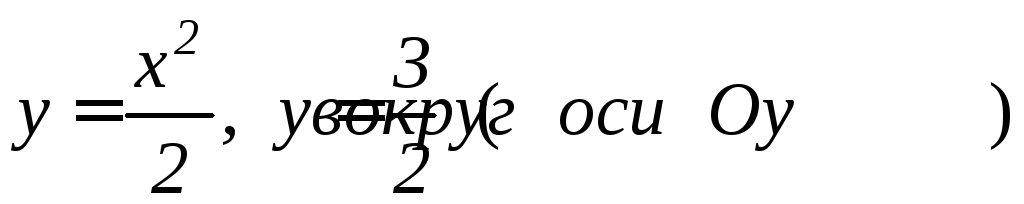 ;
;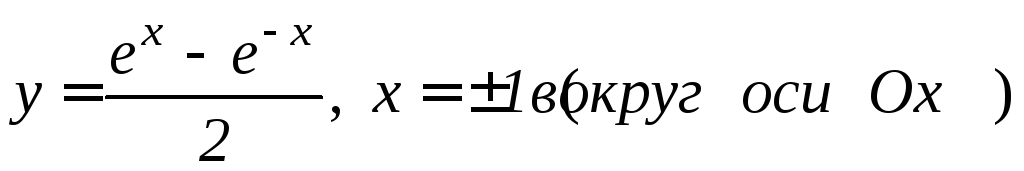 ;
;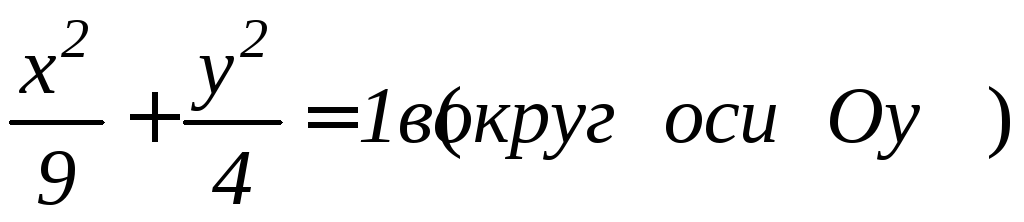 ;
;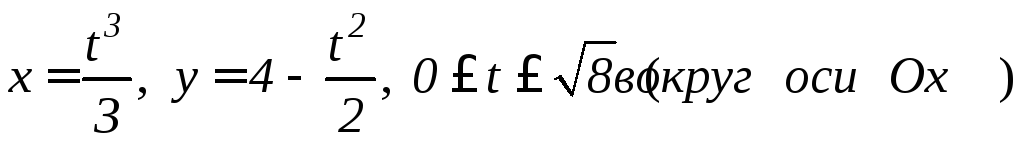 ;
;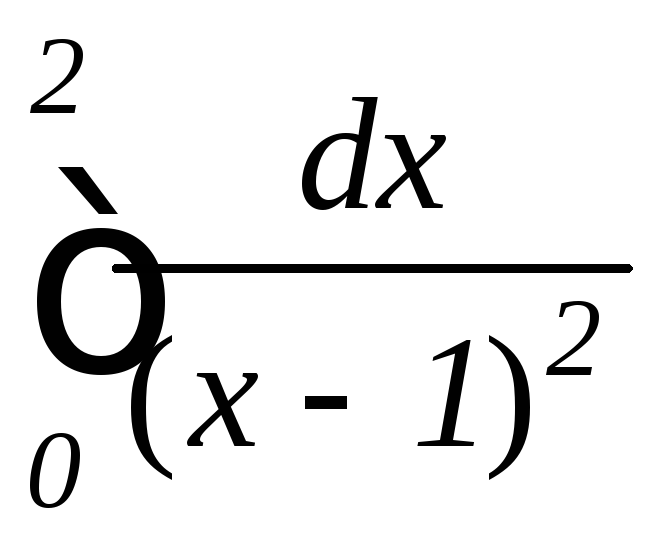 ,
б)
,
б)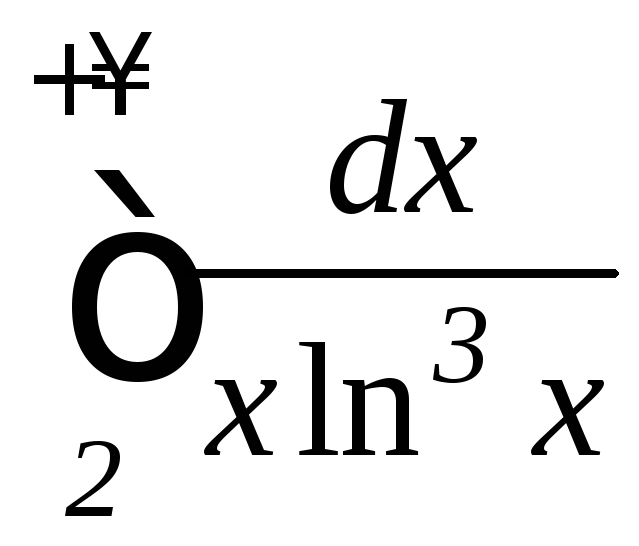 ;
;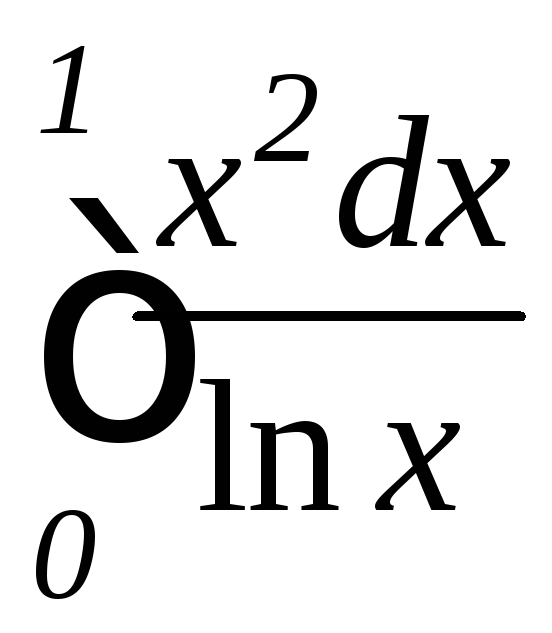 ,
б)
,
б)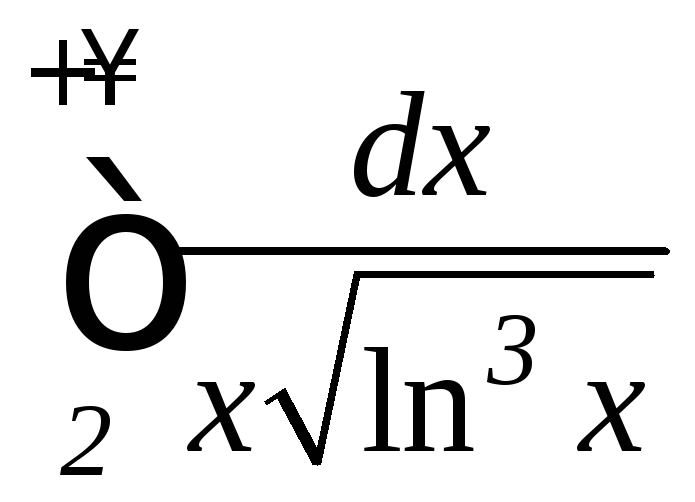 ;
;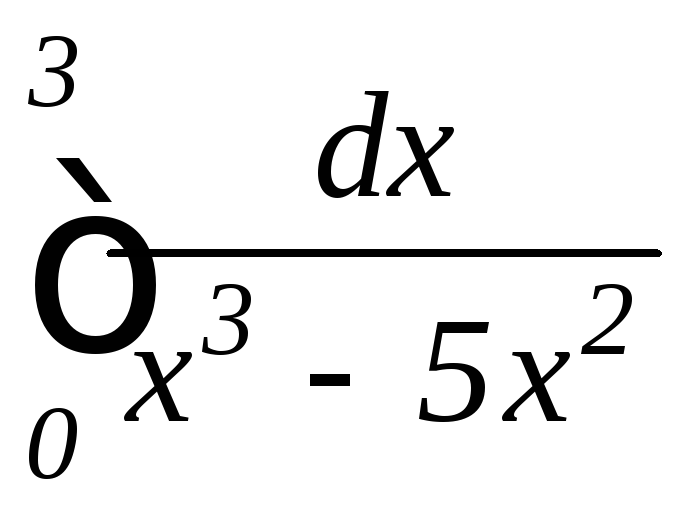 ,
б)
,
б)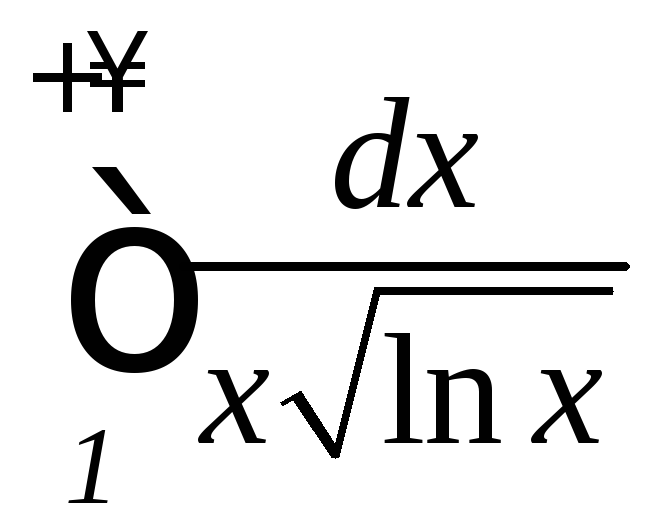 ;
;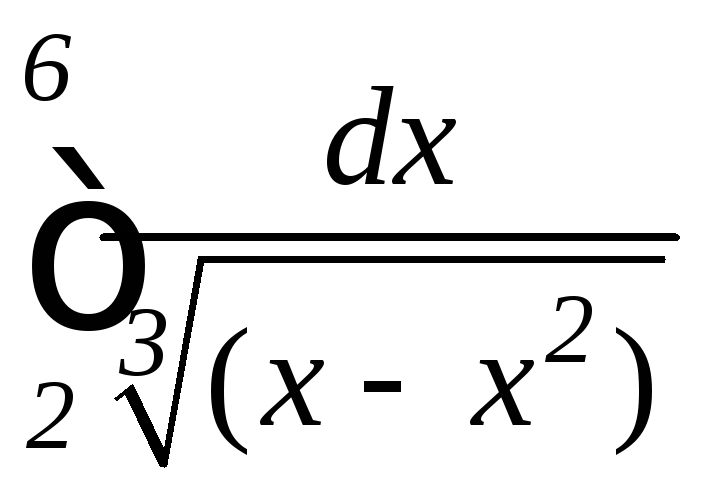 ,
б)
,
б)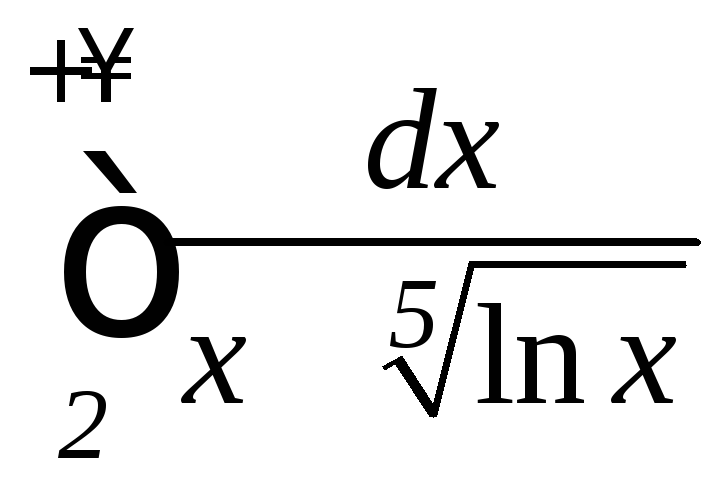 ;
;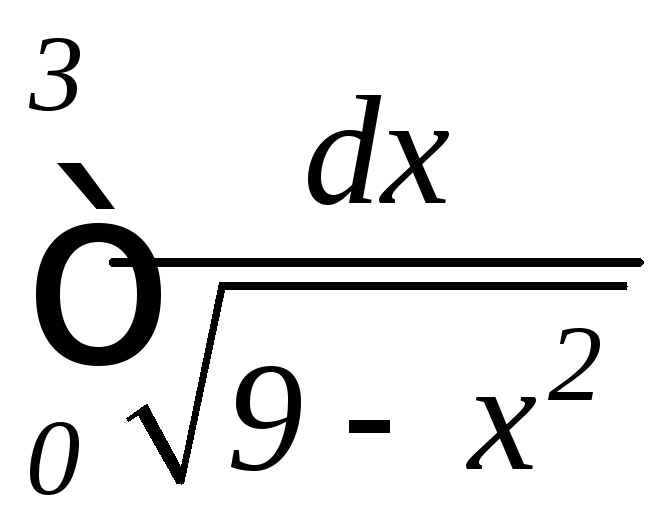 ,
б)
,
б)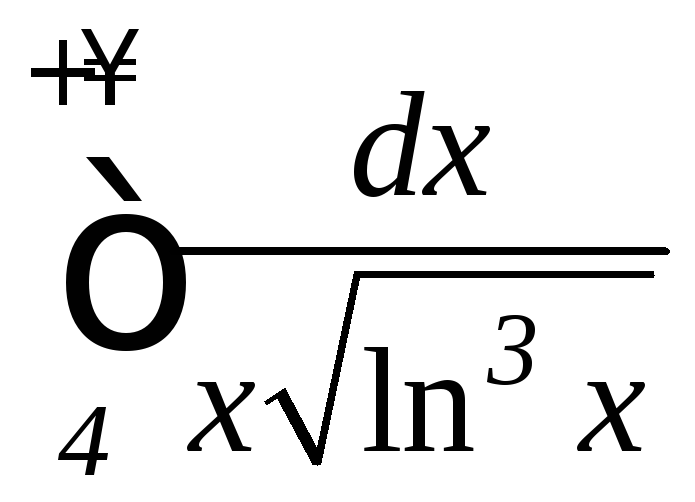 ;
;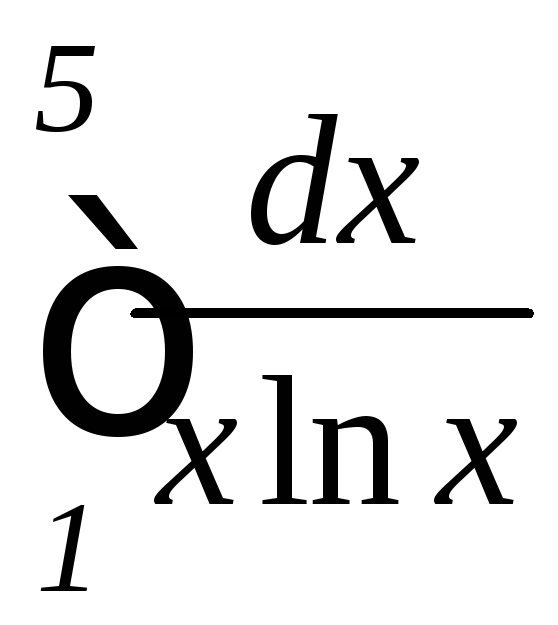 ,
б)
,
б)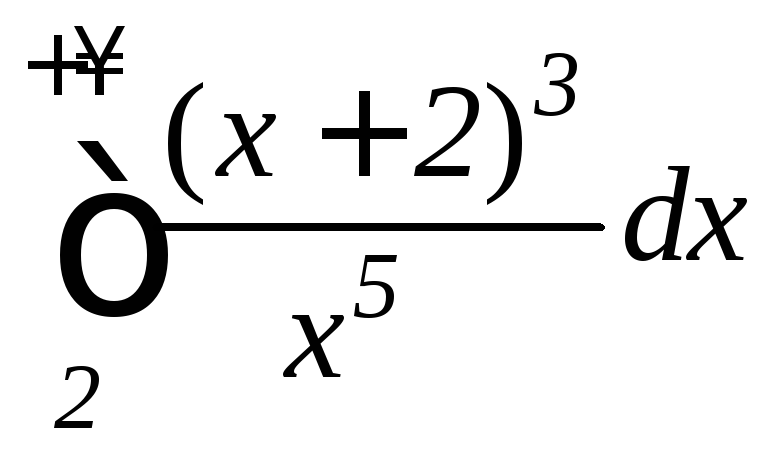 ;
;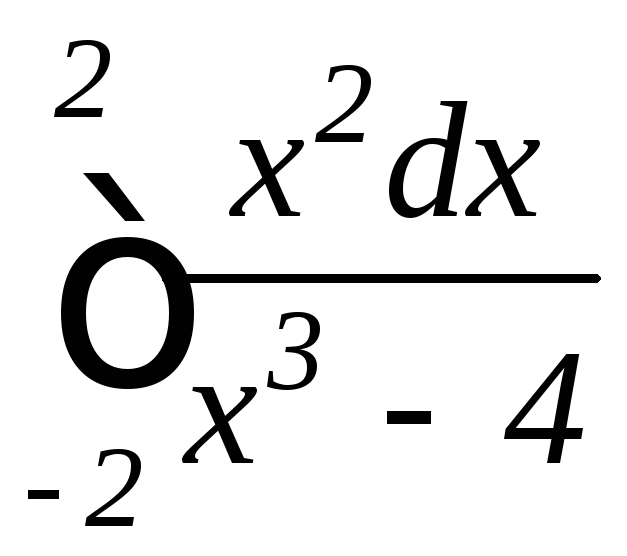 ,
б)
,
б)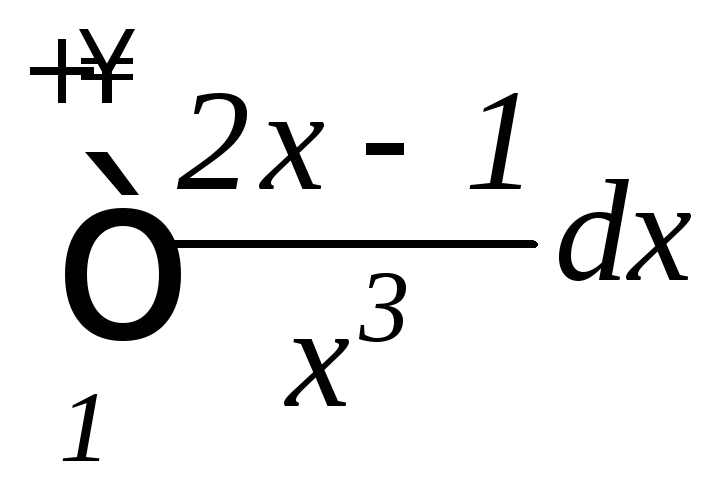 ;
;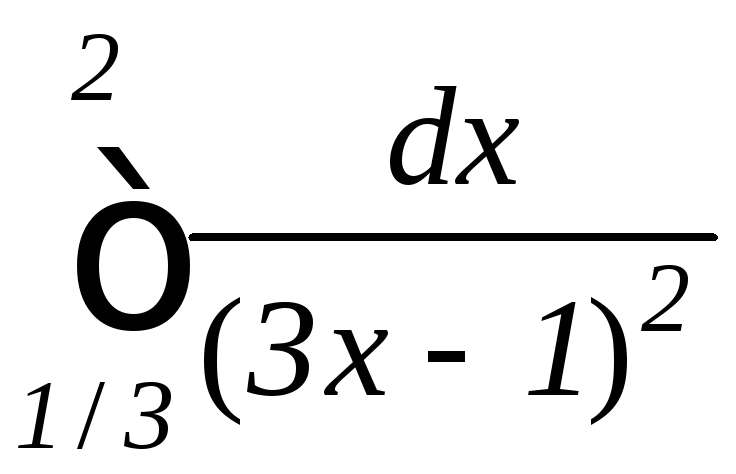 ,
,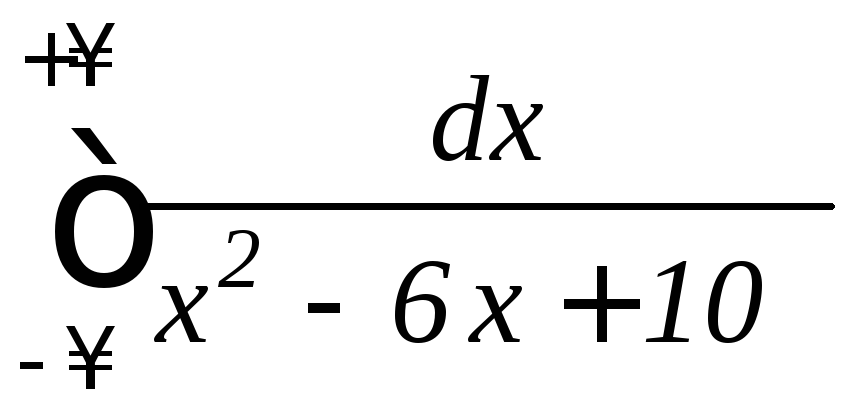 ;
;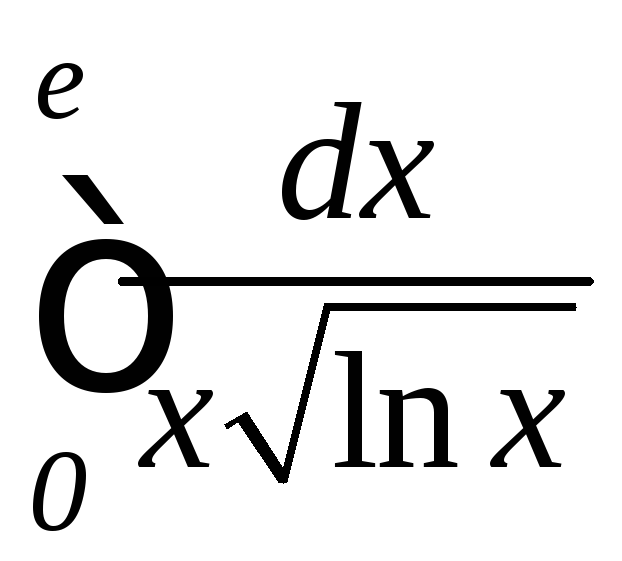 ,
б)
,
б)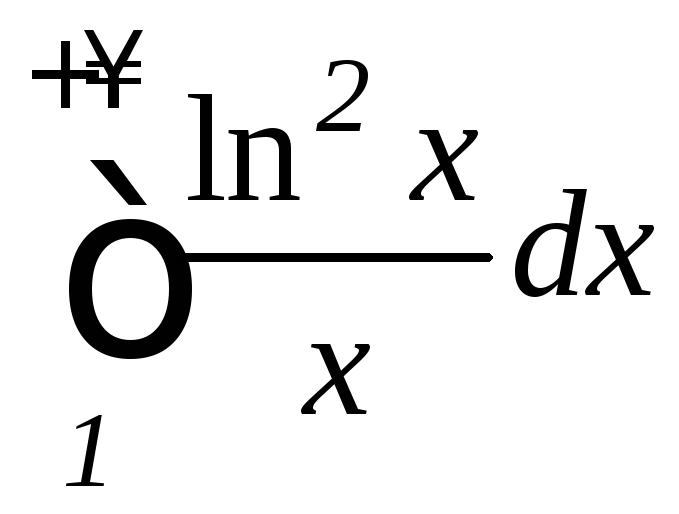 ;
;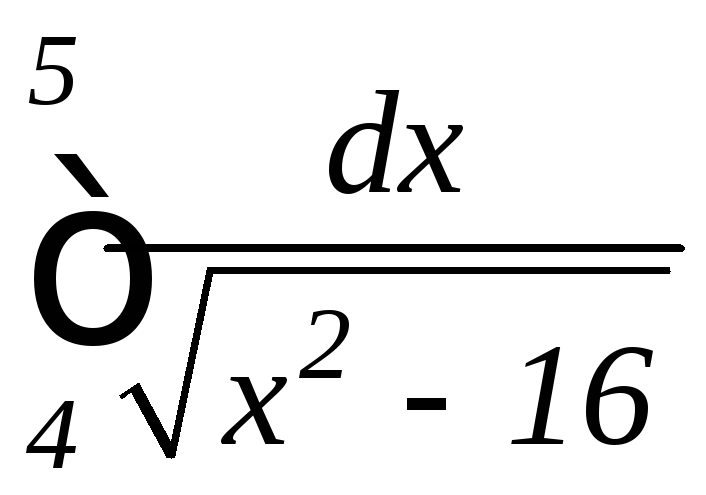 ,
б)
,
б)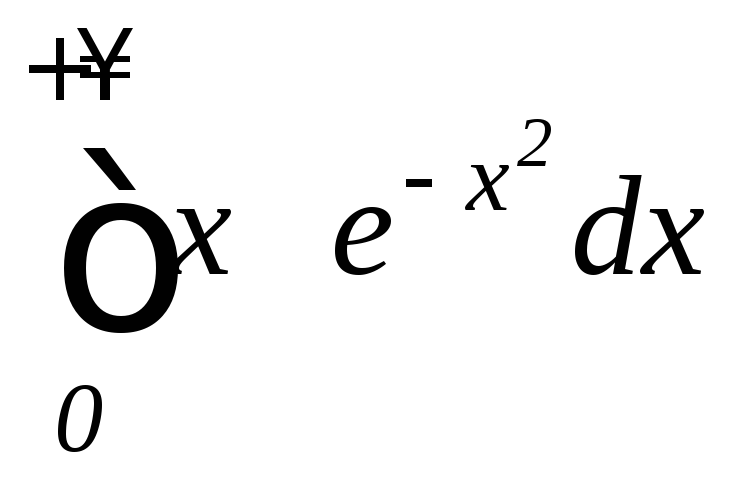 ;
;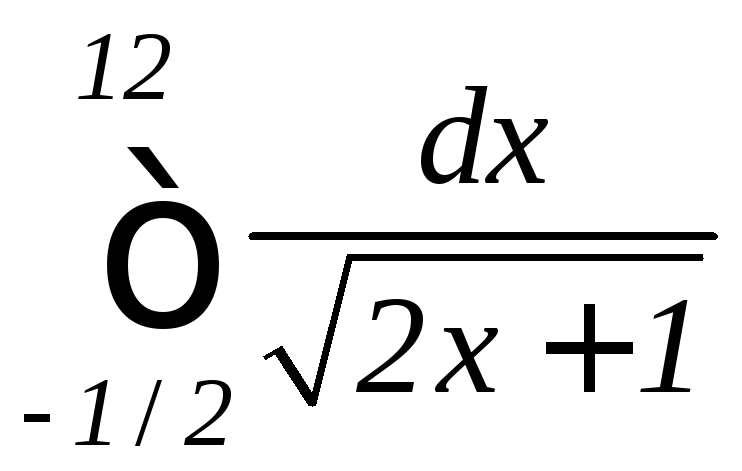 ,
б)
,
б)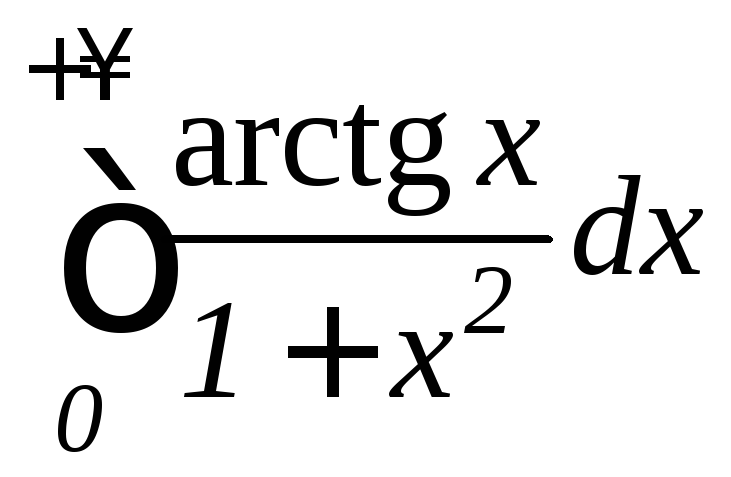 ;
;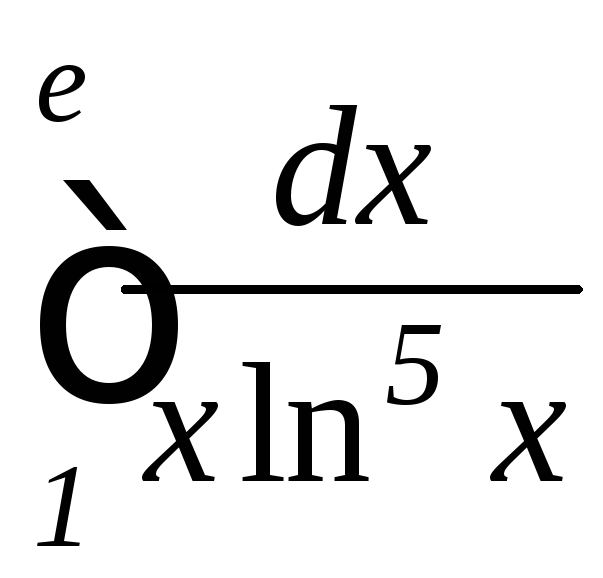 ,
б)
,
б)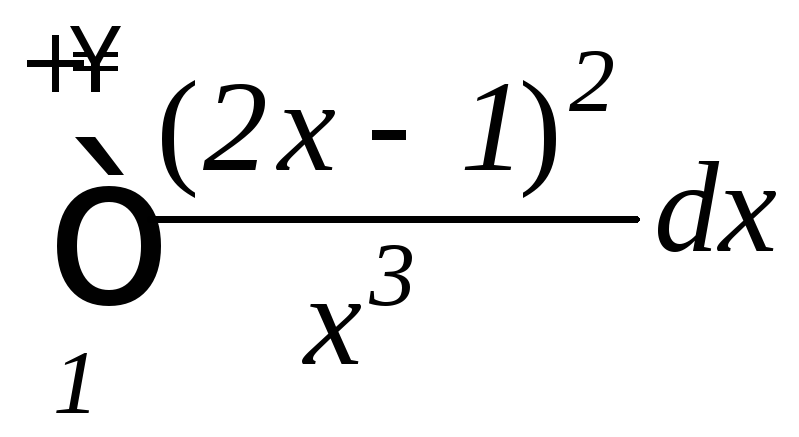 ;
;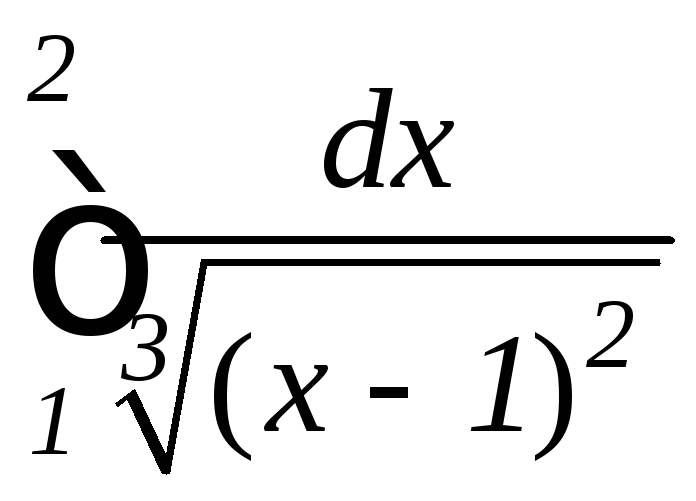 ,
б)
,
б)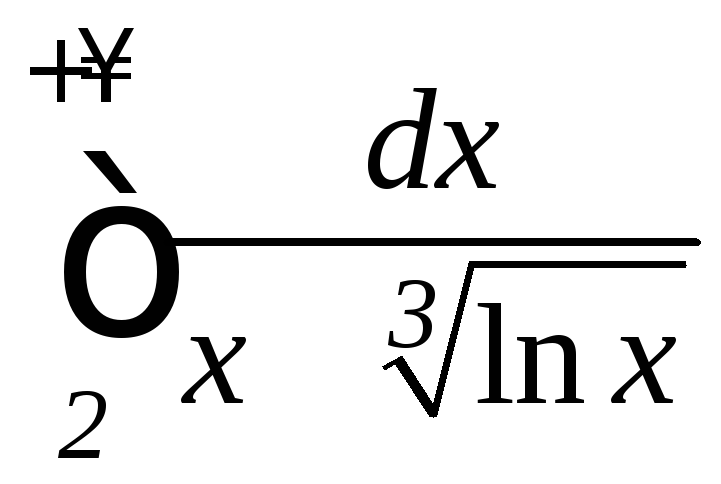 ;
;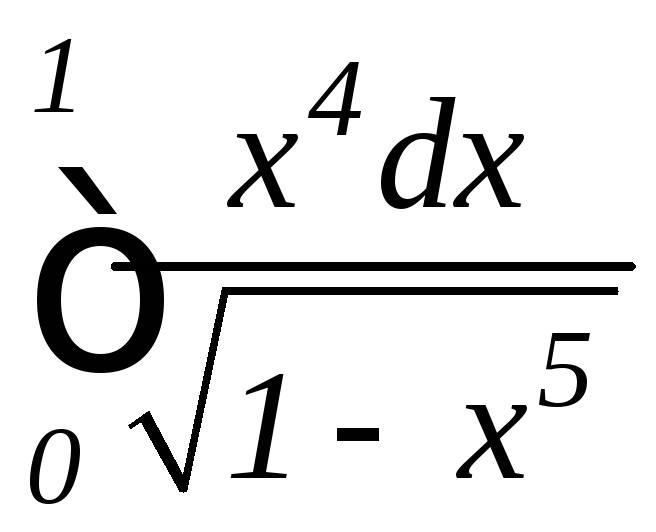 ,
б)
,
б)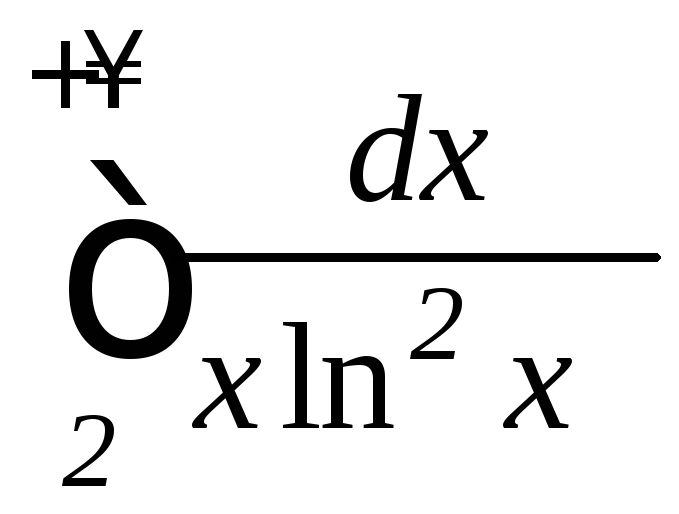 ;
;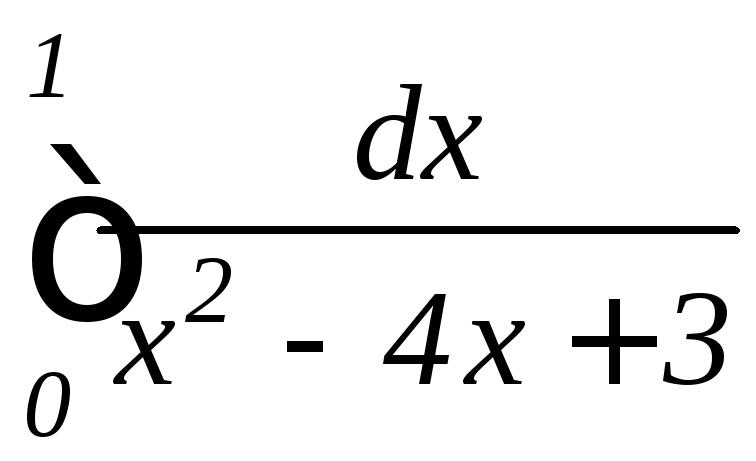 ,
б)
,
б)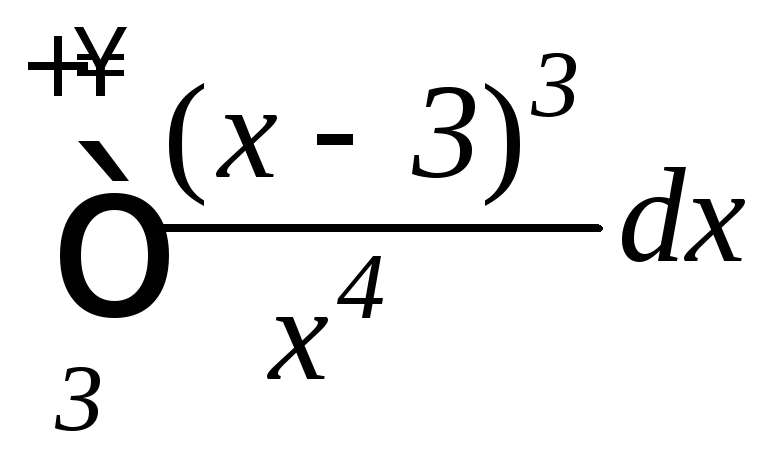 ;
;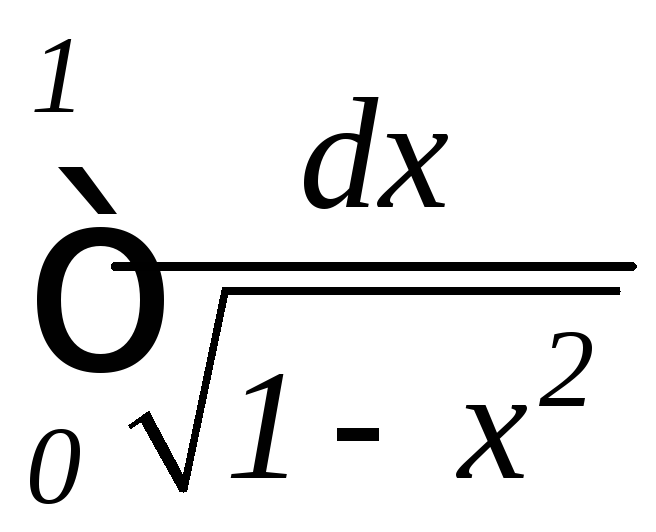 ,
б)
,
б)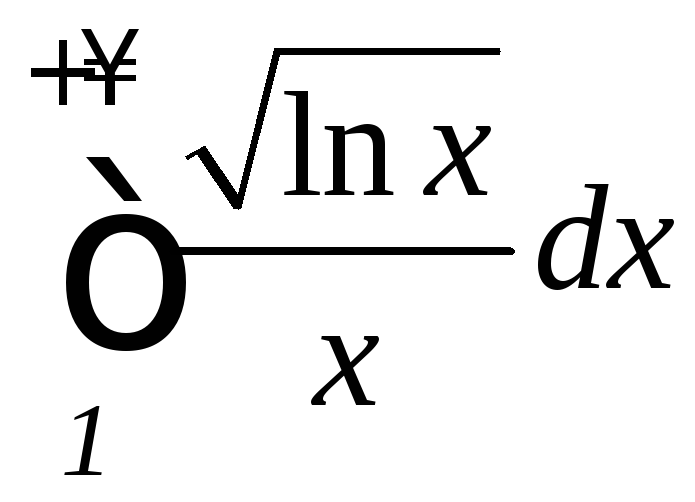 ;
;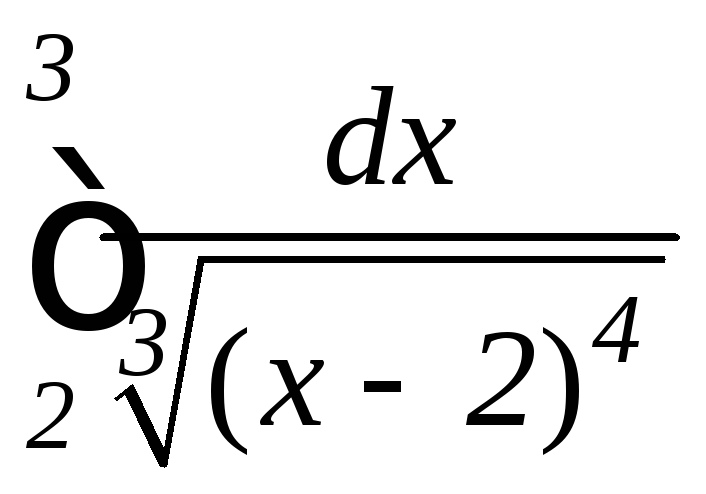 ,
б)
,
б) ;
;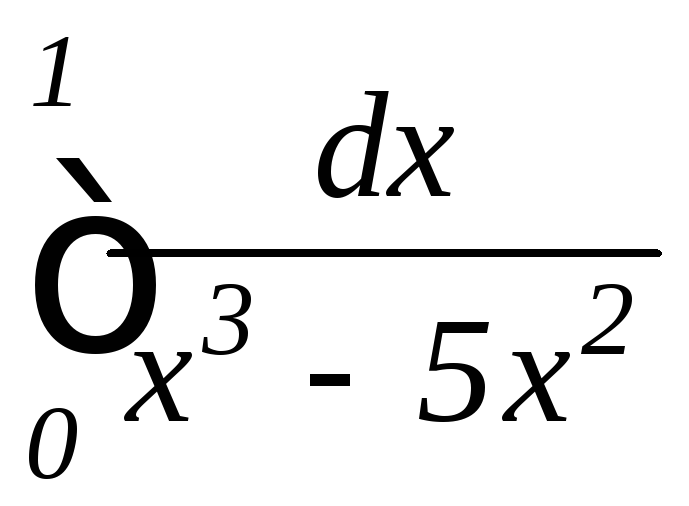 ,
б)
,
б)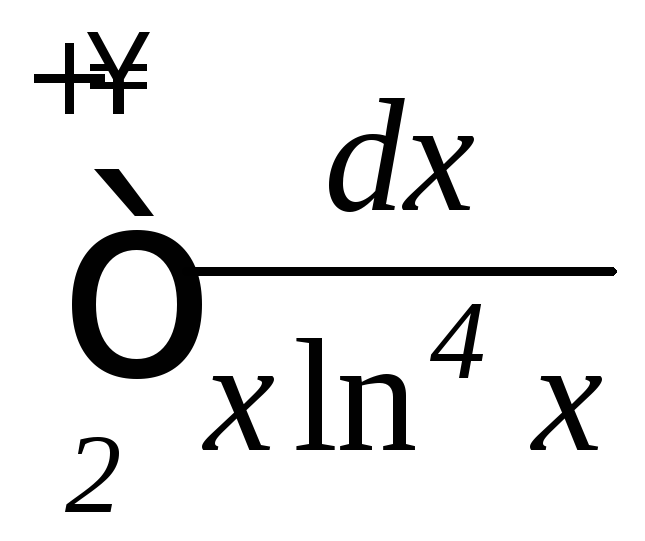 ;
;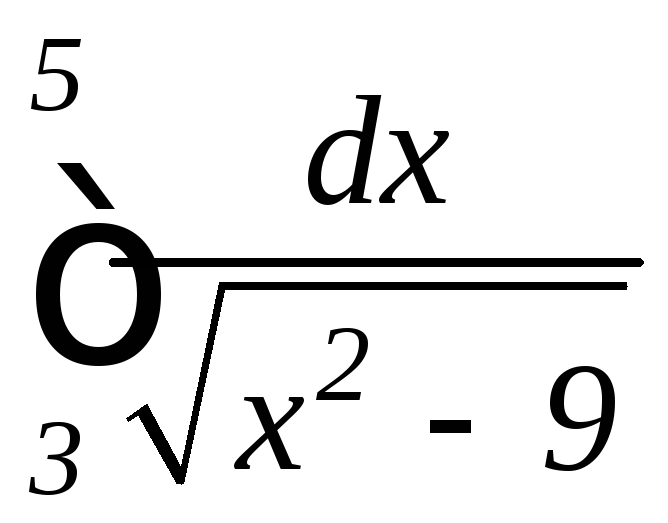 ,
б)
,
б)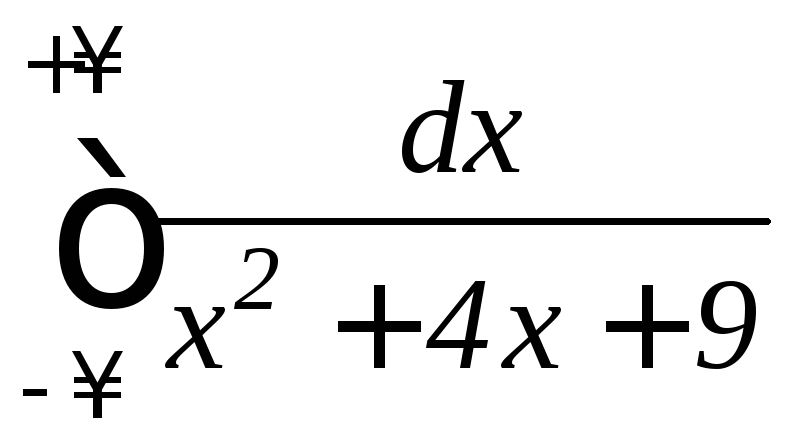 ;
;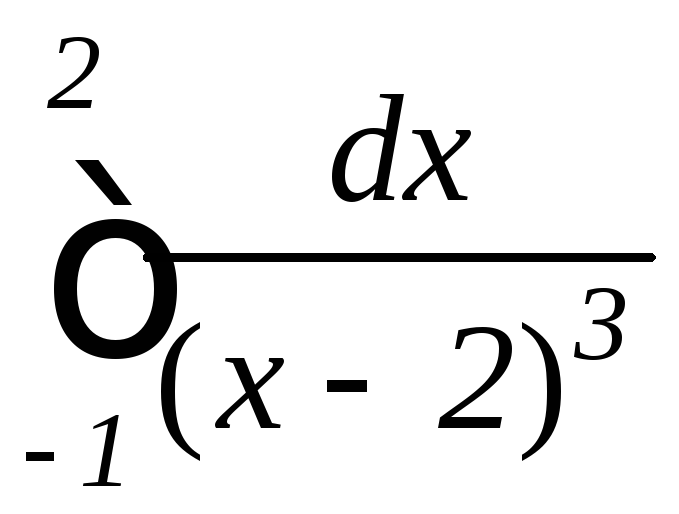 ,
б)
,
б)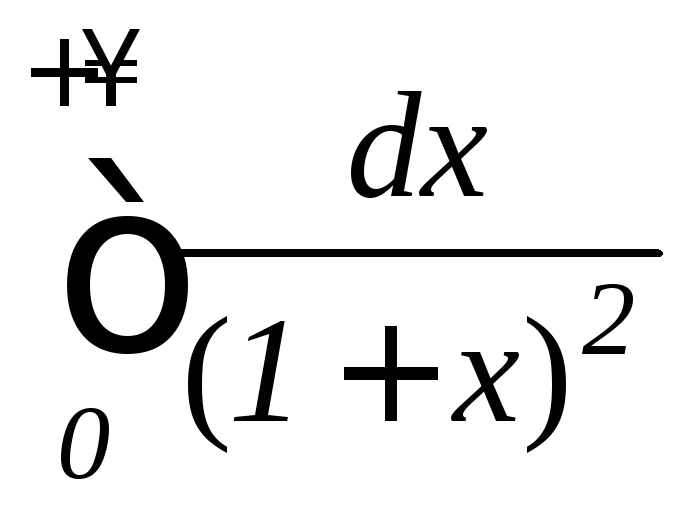 ;
;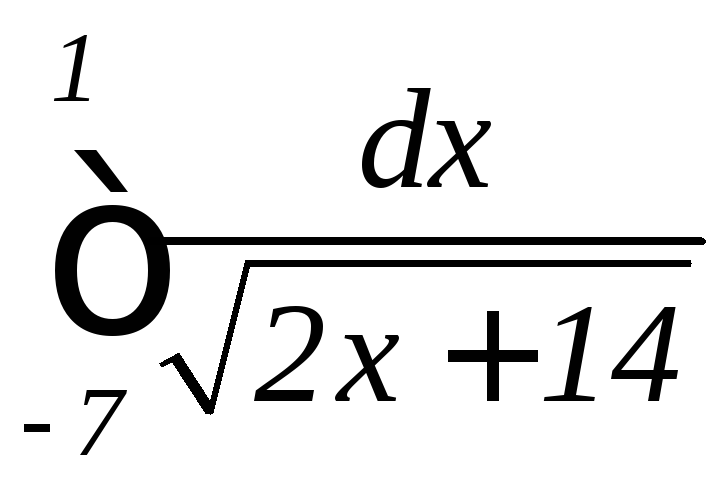 ,
,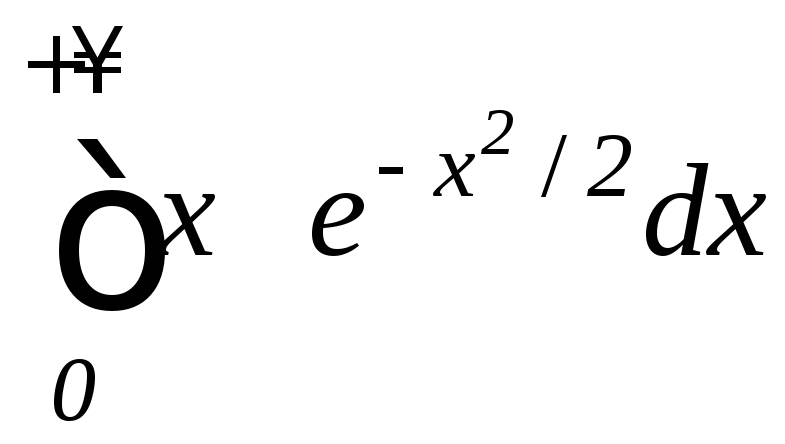 ;
; ,
,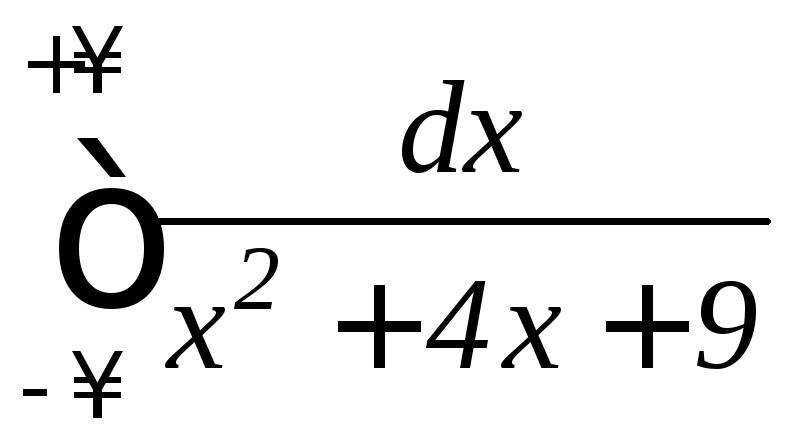 ;
;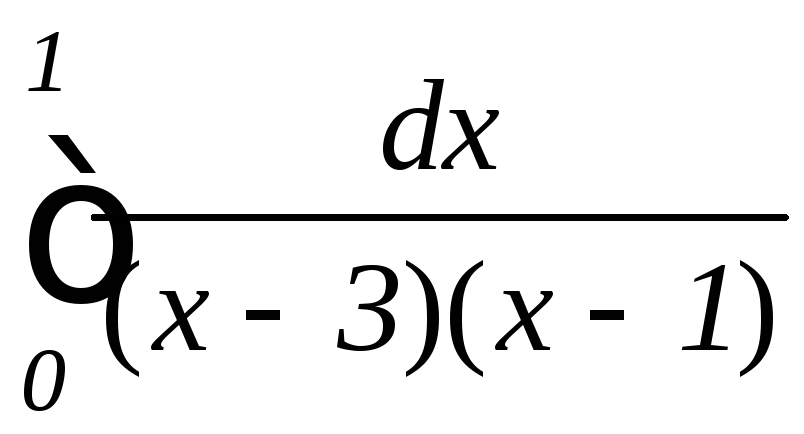 ,
,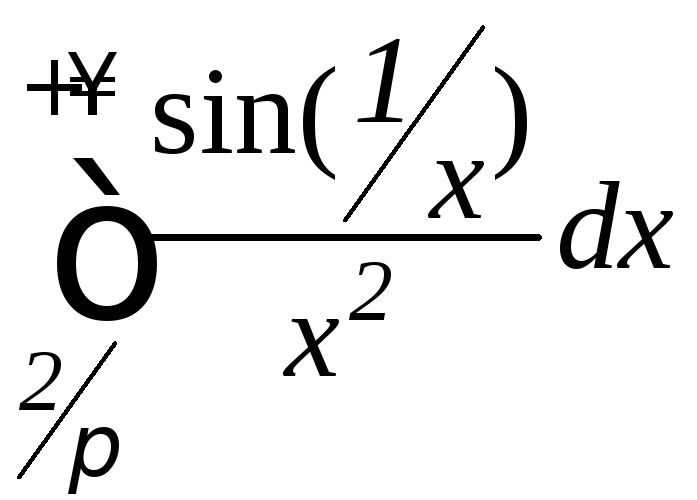 ;
;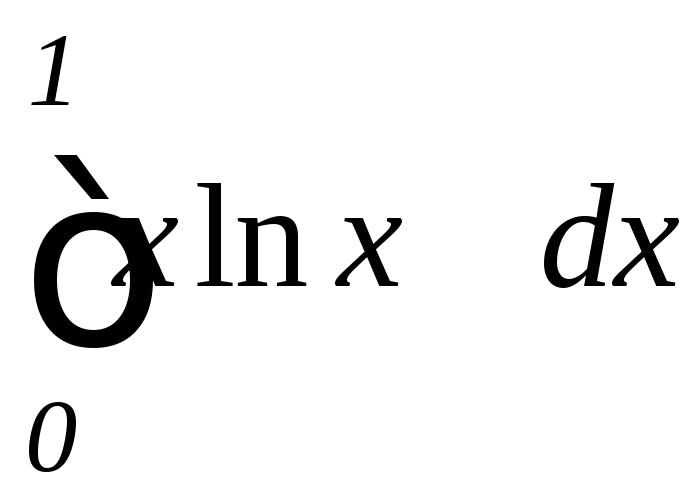 ,
,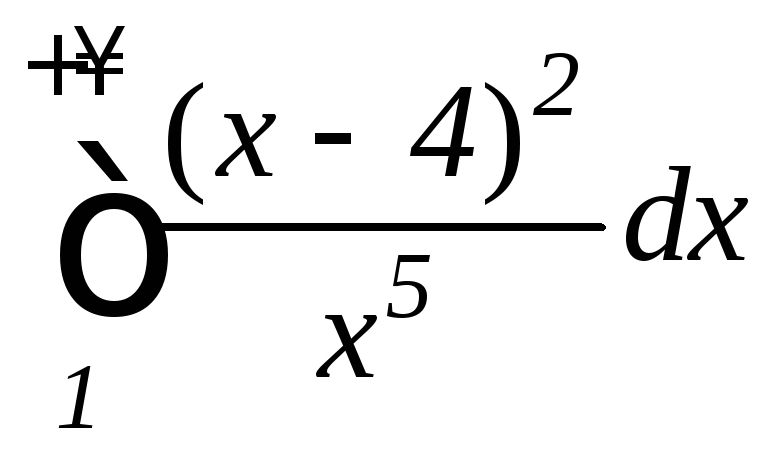 .
.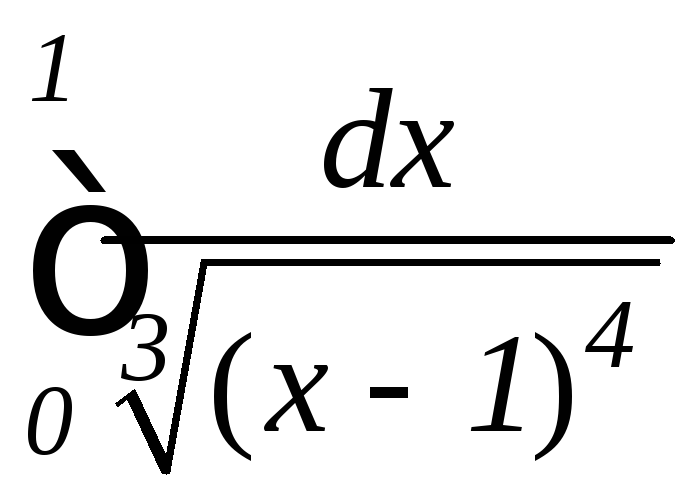 ,
б)
,
б)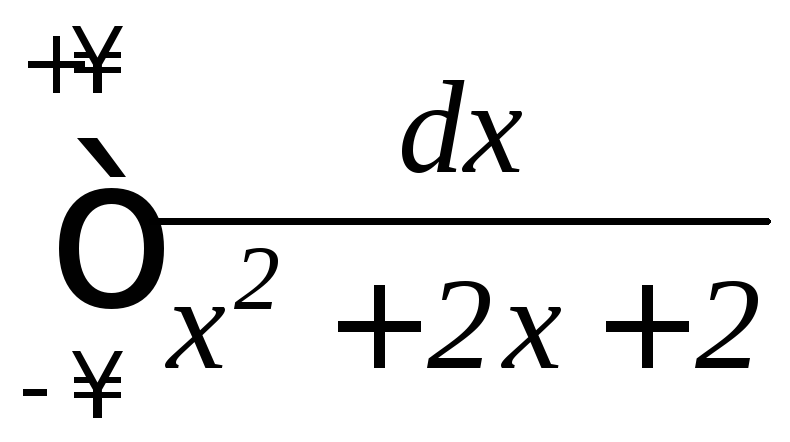 ;
;