78. Предел функции. Свойства пределов.

Преде́л фу́нкции (предельное значение функции) — одно из основных понятий математического анализа, значение, к которому функция в определённом смысле приближается при приближении аргумента к определённой точке.

Функция имеет предел А в точке х0 , если для всех значений х , достаточно близких к х0, значение близко к А .

Предел функции обозначается как , при или через символ предела .

Рассмотрим основные свойства пределов.

1)Предел суммы

Предел суммы равен сумме пределов, если каждый из них существует, т.е.

2)Предел разности

Предел разности равен разности пределов, если каждый из них существует, т.е.

3) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

4)Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

5) Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.

6) Предел частного

Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е.

7)Предел степенной функции

где степень p - действительное число.

79. Непрерывность функции, точки разрыва. Замечательные пределы.

1. Непрерывность функции в точке

Пусть функция у=ƒ(х) определена в точке хо и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.

Равенство (19.1) означает выполнение трех условий:

1) функция ƒ (х) определена в точке x0 и в ее окрестности;

2) функция ƒ(х) имеет предел при х→хо;

3) предел функции в точке хо равен значению функции в этой точке, т. е. выполняется равенство (19.1).

Можно дать еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции.

Пусть функция у=ƒ(х) определена в некотором интервале (а;b). Возьмем произвольную точку хо є (а;b). Для любого хє(а;b) разность х-хо называется приращением аргумента х в точке х0 и обозначается ∆х («дельта х»): ∆х=х-x0. Отсюда х=х0+∆х.

Разность соответствующих значений функций ƒ(х)-ƒ(х0) называется приращением функции ƒ(х) в точке х0 и обозначается ∆у (или ∆ƒ или ∆ƒ(х0)): ∆у=ƒ(х)-ƒ(х0) или ∆у=ƒ(х0+∆х)-ƒ(х0) (см. рис. 119).

2. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х=х0 — точка разрыва функции у=ƒ(х), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:

1. Функция определена в окрестности точки х0, но не определена в самой точке х0.

Например, функция у1/(x-2) не определена в точке х0=2 (см. рис. 120).

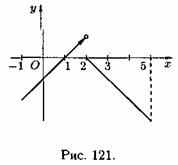
2. Функция определена в точке х0 и ее окрестности, но не существует предела ƒ(х) при х→х0. Например, функция

определена в точке х0=2 (ƒ(2)=0), однако в точке х0=2 имеет разрыв (см. рис. 121), т. к. эта функция не имеет предела при х→2:

Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

Первый замечательный предел:

Второй замечательный предел: