Уравнение судна при остановке главных двигателей.

или . Физически в этом случае имеем силу вязкого трения, которая уравновешивается силой инерции. С уменьшением скорости и сила инерции должна уменьшаться, то есть должно уменьшаться ускорение, что и будет происходить вплоть до скорости и ускорения, равных нулю.

Непосредственной подстановкой определяем, что .

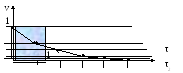
s

Рис. 9. Построение графика остановки судна

Интересной информацией, полученной из этого уравнения, является путь, который пройдет судно после остановки главных двигателей.

. Это значит, что судно пройдет путь, численно равный единице скорости, измеренной в относительных единицах времени (с базовым значением времени Та), то есть за время Та. В последней колонке приведенной выше таблицы дано значение этой скорости численно равной искомому пути. Как видим, этот путь не малый, от половины до километра. Поэтому при швартовке реверс движителей необходим для торможения судна.

1.6. Основы механики вращения

Судовой электромеханик в основном имеет дело с вращающимися механизмами.

Аналогом силы во вращательном движении является момент. Момент – векторное произведение плеча R на силу F (см. рис. 10) M=RxF.*

Кинематика вращения такова.

Аналогом перемещения радиуса является угловое перемещение Ω в радианах. Радиан – rad - это единица углового перемещения на длину дуги равную радиусу окружности.

Как известно, длина окружности равна 2πR. Перемещение по кругу, таким образом, равно 2π радианам.

*) Векторным произведением называют вектор, направленный перпендикулярно плоскости образованной двумя векторами – сомножителями. Вектор направленный так, что первый вектор при своем условном (мысленном) повороте в сторону сближения со вторым вектором движется против часовой стрелки. Длина вектора равна произведению модулей векторов на синус угла между ними.

Рис. 10. Кинематика вращения механизмов

Угловое перемещение считается положительным, если оно совершается против вращения часовой стрелки, если смотреть с конца оси, обращенной к приводу (аналогично вращению Земли, если смотреть со стороны Северного полюса). Таким образом, угловое перемещение это тоже вектор Ω. Угловая частота вращения ω равна величине углового перемещения за единицу времени ω=Ω/Т=(L/R)/Т.

Работа силы за один оборот равна А= F•2πR = 2π •FR =2π •M. То есть работа силы за один оборот равна 2π моментов.

Мощность P=A/T=M•Ω/T=M•ω. Величину ω называют угловой частотой вращения.

Все указанные жирным шрифтом величины являются векторными. На рис. 10 все величины имеют положительное направление вектора по оси Х, так как, если смотреть со стороны направления положительной оси, то движение и направление момента вращающей силы будут видны против часовой стрелки. Длина вектора численно равна соответствующей величине. Динамика вращения с учетом изложенных положений кинематики будет следующая.

Предположим, что на конце радиуса находится материальная точка с массой М (пишется курсивом, чтобы отличить от обозначения момента М). На эту точку действует сила F. Точка движется с линейной скоростью V=L/T= (L/R)•R/T=(Ω/T)•R=ω•R

Сил без противосил не бывает. Значит, материальная точка должна двигаться с ускорением М•ω•R/t =F. Умножим обе части равенства на R, чтобы от силы перейти к ее моменту. М• R •R•ω /T =F•R. Или М• R²•ω /t =М. Или М= М• R²•ω /t. То есть, момент силы равен так называемому инерционному моменту, который в свою очередь равен М• R²•(ω /t), где ( ω /t) – угловое ускорение. При t0 имеем М• R²•d/dt=M. То есть просматривается следующая аналогия с инерционной средой при поступательном движении (F=M•а, или более грамотно с учетом анализа бесконечно малых величин F=M•dv/dt). Роль массы при вращении играет величина М• R², которая называется моментом инерции и обозначается J= М• R².= М• (D/2)²= М• D²/2²== М• D²/4. Известно, что в начале люди не отличали массу от веса, так как на Земле численно масса равна весу. Поэтому величина М• D² получила название GD² – маховой момент. Эта величина GD² дается во всех справочниках. Таким образом, если сила измеряется в Ньютонах, надо справочную величину GD² (маховой момент) разделить на четыре и получить момент инерции J= GD²/4.

Получаем следующее уравнение динамики вращающихся масс

J•dω/dt=M. Соответственно, если на вал будут действовать, как движущие силы по направлению вращения, так и тормозящие силы нагрузки, то справа будем иметь разность моментов движения и торможения – нагрузки.

J•dω/dt=M_дв-М_н. Это и есть уравнение движение в физических величинах.

Перейдем к относительным величинам. Для этого разделим обе части равенства на номинальный момент М_N. Обозначим M_дв/ М_N=μ, М_Н/ М_N=λ. Кроме того обозначим относительную угловую частоту вращения через φ=ω/ω_N. Заметим, что ω_N=2πN/60, где N есть номинальное число оборотов в минуту. Преобразуем уравнение в физических величинах в уравнение в относительных величинах.

(J• ω_N/M_N)• d(ω/ω_N)/dt=M_дв/ М_N -М_н/ М_N или

(J• ω_N/M_N)• dφ/dt=μ-λ.

Величина J• ω_N/M_N носит название механической постоянной времени агрегата, и обозначается Т_а. Она дается в справочниках для конкретного агрегата или ее можно получить, зная номинальную частоту вращения, маховой момент агрегата и вычислив номинальный момент (с учетом знания номинальной частоты вращения и номинальной мощности механизма). Окончательно получаем уравнение динамики вращающегося агрегата.

T_a• dφ/dt=μ-λ. где Т_а – механическая постоянная времени,

 - относительное значение движущего момента,

λ – относительное значение тормозного момента.

Обсудим полученный результат. В этом уравнении:

φ – выход.

 - вход 1.

λ – вход 2.

Рис. 11. Структура вращающегося агрегата

Вращающийся агрегат по своей структуре представляет собой интегральное звено с входом (-λ) (1/Та). Если (-λ)>0, то выход будет непрерывно увеличиваться вплоть до бесконечности, если (-λ)<0, то выход будет непрерывно уменьшаться вплоть до минус бесконечности. Иначе говоря, если вход не будет равен нулю, то агрегат пойдет в «разнос». Избежать разноса можно только сделав зависимость  или λ от φ. Так и получают, с помощью различного рода регуляторов или естественной зависимости λ от φ.

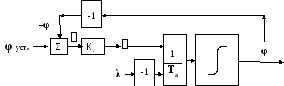Рис. 12. Структура объекта с регулятором частоты

На рис. 12 объект дополнен регулятором частоты с отрицательной обратной связью по частоте вращения. В его состав входят инвертор, меняющий знак φ, сумматор, на выходе которого появляется разность  между уставкой, задающей желаемое значение частоты, и частотой на выходе из объекта. Эту разность называют ошибкой регулирования, так как она показывает отклонение реальной частоты от заданной. Ошибка поступает на усилитель с коэффициентом Ку, который и формирует регулирующее воздействие , как правило, требующее усилий по передвижению рейки топливного насоса, штока клапана и др. В установившемся режиме =*Ку=ג. Только при этом условии объект не пойдет в разнос. Тормозной момент ג задается работой механизмов на валу агрегата, которые называются приводом. Привод в свою очередь обеспечивает нужды судна. Поэтому это внешний фактор, под который должно подстроиться регулирующее воздействие . Из приведенного равенства видно, что при таком регулировании ошибка  неизбежна. Причем, чем больше тормозной момент ג, тем больше ошибка. Но чем больше Ку, тем ошибка становится меньше, и точность повышается . Однако беспредельно Ку увеличивать нельзя, так как система в целом перейдет в колебательный режим (подробно об этом излагается в теории автоматического управления, что выходит за рамки данного обсуждения). Наоборот, если появились колебания, то первым делом надо уменьшить коэффициент усиления регулятора, пожертвовав точностью регулирования. Изменение Ку является предметом настройки регулятора наряду с другими факторами. Ошибка в процентном отношении при номинальном режиме, ג=1, носит название «статизм» или «неравномерность регулирования», на английском языке «droop». Этот весьма важный параметр для эксплуатации параллельно работающих механизмов обычно равен 3%. Предусматривается механизм для его настройки от 2 до 6%.

Регулятор можно не делать, если имеем характеристику привода, зависящую от частоты вращения. Например, если приводом является винт судна, то регулирование скорости судна можно осуществлять только лишь изменением . Известно, что винтовая характеристика имеет квадратичную зависимость от частоты вращения. При такой характеристике происходит саморегулирование объекта, см. рис. 13.



ג

= ג

Рис. 1

= const

*

ג=φ²

Точка равновесия

φ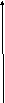

3. Пимер саморегулирования

Это свойство саморегулирования (обратная связь через среду с которой взаимодействует объект) часто применяется на малых судах, катерах и яхтах. При этом устройство двигателя значительно упрощается. Структура такого саморегулирования показана на рис. 14.

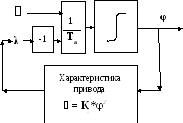
Рис. 14. Структура объекта с саморегулированием

В заключение скажем, что вопрос регулирования и настройки, а также проектирования устойчивой системы (вращающийся механизм – привод) зависит от комплекса конкретных условий, простейшие, из которых, были рассмотрены в настоящем разделе.

Задачи для самопроверки

1. Основное уравнение движения известно (сила F равна сумме противосил, которые пишут справа от знака равенства):

F – сила,

M – масса, V – скорость (ds/dt), s – перемещение,

Квт – коэффициент вязкого трения,

С – жесткость упругой среды.

Как правильно сказать:

1. движение всегда будет таким, чтобы была равная противосила.

2. если приложена сила, то появится движение тела.

3. сила будет толкать тело, и потому оно будет двигаться.

Не нужное зачеркнуть.

2.

Тело массой M, имеющее вес G, покоится на поверхности.

Убрали мгновенно поверхность. Исчезнет ли противосила весу?

Да,

Нет. Не нужное зачеркнуть.

3. Тело массой M, имеющее вес G, покоится на поверхности.

Убрали мгновенно поверхность.

Как будет двигаться тело после того, как убрали поверхность?

1. С ускорением g=10м/c².

2. Равномерно.

3. Останется на месте.

Не нужное зачеркнуть.

4. Как будет двигаться система тел?

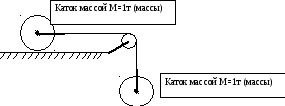
Один каток пустили по абсолютно гладкой поверхности, другой подвесили на весьма прочной нити. Сопротивлением воздуха пренебречь.

1. будет двигаться равномерно,

2. будет двгаться с ускорением 10м/с*с

3. будет двгаться с ускорением 5м/с*с

4. будет двгаться с ускорением 15м/с*с

Не нужное зачеркнуть.

5. Как будет двигаться система тел через достаточно большое время, когда переходный процесс закончится?

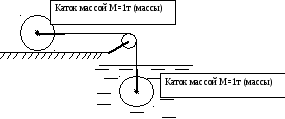
Один каток пустили по абсолютно гладкой поверхности, другой подвесили на абсолютно прочной длинной нити и поместили в вязкую жидкость. Сопротивлением воздуха пренебречь.

Будет двигаться равномерно,

будет двгаться с ускорением 10м/с*с

будет двгаться с ускорением 5м/с*с

будет двгаться с ускорением 15м/с*с

Не нужное зачеркнуть 6. В безвоздушное пространство внесли тело со скоростью V скользящее по абсолютно гладкой поверхности. Какая скорость тела будет через достаточно длительное время?

Остановится, и скорость тела станет равной нулю,

останется той же и будет двигаться равномерно,

будет двгаться с ускорением 10м/с*с,

будет двгаться с ускорением 5м/с*с,

будет двгаться с ускорением 15м/с*с,

Н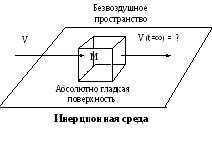е нужное зачеркнуть 7. Как правильно записать расход топлива дизеля (с точки зрения теплотворной способности топлива):

0,1 кГ/час,

0,1 кг/час,

0,1 кг/час,

0,1 кгс/час,

ненужное зачеркнуть.

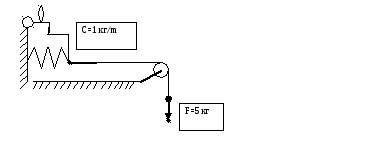
8. К пружине с защелкой приложили силу 5 кг и мгновенно открыли защелку.

Как будет двигаться конец пружины?

Останется в том же положении,

будет двигаться равномерно,

будет двгаться с ускорением 10м/с*с,

сделает скачек на 5 м

сделает скачек на 1 м

Не нужное зачеркнуть

9. Рассмотреть какие силы и какое движение будет на участках пути с различными подъемами в случае, когда действуют источники силы и источники скорости. Считать, что вагон не имеет размеров (считать вагон материальной точкой, имеющей массу, но не имеющей размеров). Задачу решить самостоятельно и обсудить решение с преподавателем.

Уклон пути 45^о

Уклон пути 45^о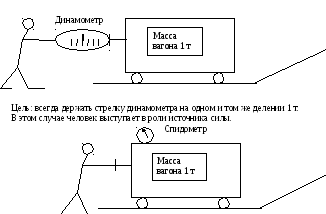

.

Цель: всегда держать стрелку спидометра на одном и том же делении 1 м/с при условии, что в начальный момент, когда передали движение человеку, скорость уже была 1 м/с.

В этом случае человек выступает в роли источника скорости.

11. Какими источниками являются поршневая помпа зачистки трюма и центробежный осушительный насос определенной производительности? Каковы важные для безопасности конструктивные особенности этих устройств?

В следующих задачах проверить правильность ответов.

12. Момент вращения 100 Нм. Частота вращения 300 об/мин. Какая мощность на валу? Ответ 3140Вт, 3,14 кВт.

13 Момент вращения 100 кГм. Частота вращения 300 об/мин. Какая мощность на валу? Ответ 31400Вт, 31,4 кВт.

14. Мощность на гребном валу судна типа «Ладога» около 640 кВт. Частота вращения 300 об/мин. Какой момент главного двигателя? Ответ 20382 Нм, 2038,2 кГм

15. По справочнику механизм имеет GD²=80 кГм²

Какой момент инерции механизма? Ответ 20 кгм²