Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

DPA_2011_mat-9-rozvyazannya-vsx-zavdan

.pdf

Скачиваний:

Добавлен:

15.02.2015

Размер:

2.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

60 ВАРІАНТ 20

1.3.Пара чисел є розв’язком системи рівнянь, якщо вона задовольняє обидва рівняння. Оскільки

3−2 =1≠ −1, −3−2 = −5 ≠ −1, 2−3 = −1 і 2+3 =5, −2−3 = −5 ≠ −1, то розв’язком системи рівнянь є пара чисел (2;3).

Відповідь. В).

1.4.−2x+3 = −3, −2x = −6, x =3.

Відповідь. А).

1.5.Помножимо обидві частини рівняння на –1: x2 −5x+6 =0. Тоді за теоремою Вієта x1 =2, x2 =3.

Відповідь. Б).

15+3(x −5)

15+3x −15

1.6.

x2 −5x

x(x −5)

x −5

Відповідь. В).

bn =b1 qn−1

1.7.

. Тоді b4 =b1 q3 = −32

−

= −32

−

=4.

Відповідь.

Б).

1.8.

Оскільки периметр рівностороннього трикутника зі стороною a дорівнює P =3a, то

4 3<3a <7 3. Отже, 12< P<21.

Відповідь. Г).

1.9.Оскільки відрізки дотичних до кола, проведених з однієї точки, рівні, то AK = AN.

Відповідь. В).

1.10. З прямокутного трикутника ABC:

AC = AB2 + AC2 = 122 +162 =20 (см).

Відповідь. А).

1.11.Нехай a+b =c, c (−2+3;1+(−4)), c (1;−3).

Відповідь. Б).

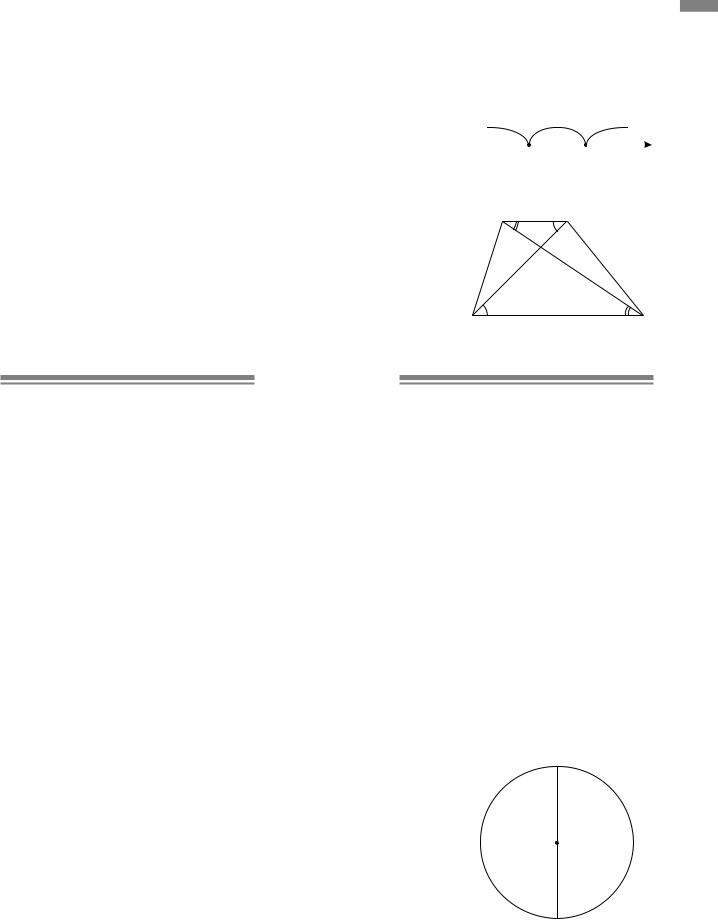
1.12. Нехай у паралелограмі ABCD A =45°. Тоді

B =180°−45°=135°. Більшою діагоналлю паралелограма

єта, яка лежить проти тупого кута, тобто діагональ AC.

Зтрикутника ABC за теоремою косинусів

AC2 = AB2 + BC2 −2 AB BC cosB.

Враховуючи, що cos135°= − 22 ,

AC2 =(2 2 )2 +52 +2 5 5	2	=53, AC = 53 .
	2

Відповідь. В).

Частина друга

2.1. 3,2 10−2 +2,1 10−3 =3,2 0,01+2,1 0,001= 0,032+0,0021= 0,0341=3,41 10−2 .

Відповідь. 3,41 10−2 .

	1		27	= −	1	2		27		27
2.2.		b					b2		= −		= − 3 .
2.2.		b					b2		= −		= − 3 .
	3		b2		3			b2		9
	Відповідь. −				3 .

ВАРІАНТ 20

2.3.

З першої нерівності системи дістанемо: 2x <9, x <4,5. Для

розв’язання другої нерівності системи знайдемо корені

рівняння 4x2 −4x−3 =0: x1 = −0,5, x2 =1,5.

–

Розв’язком другої нерівності системи є (−∞;−0,5

1,5;

+ ∞).

–0,5

1,5

Оскільки x <4,5, усі розв’язки системи нерівностей належать

(− ∞;−0,5] [1,5;4,5). З них натуральними є числа 2, 3 і 4.

Відповідь. 2, 3, 4.

2.4.

Оскільки трикутники AOD і COB подібні (за двома кутами),

то

. Нехай OB =x см, тоді OD =(x+2)

см. Отже,

x +2

, звідки x =4. OB =4 см, OD =6 см.

Відповідь. 4 см; 6 см.

Частина третя

3.1.Нехай швидкість руху першого туриста x км/год, а швидкість руху другого туриста y км/год. Тоді перший турист до зустрічі пройшов 2x км, а другий — 2y км. 2x+2y =20. На весь шлях

першому туристу знадобиться

год, а другому —

год, що на 1 год 40 хв =

год менше

від часу руху першого туриста.

2x+2y =20,

x+y =10,

y =10−x,

Маємо:

−

;

−

=0;

−

=0.

−x

Розв’язавшидругерівняннясистеми,дістанемо:

60(10 −x) −60x −5x(10 −x)

=0, x2 −34x+120 =0,

3x(10 −x)

x1 =

34 +26

=30 — не задовольняє умову задачі, x2 =

34 −26

=4. Отже, перший турист рухався

зі швидкістю 4 км/год, а другий — 10−4 =6 км/год.

Відповідь. 4 км/год, 6 км/год.

3.2. Перепишемо

даний

вираз

вигляді

x2 +2x+1−1+y2 −4y+4−4 = (x+1)2 −1+(y−2)2 −4 =

=(x+1)2 +(y−2)2 −5. Найменше значення виразу (x+1)2

дорівнює нулю при x = −1, найменше

значення виразу (y−2)2

дорівнює нулю при y =2. Отже, найменше значення заданого виразу

дорівнює –5.
Відповідь. –5.	C
	C

3.3.За властивістю хорд кола, що перетинаються в точці O,

CO OD = BO AO.	умовою CD AB, то AO = BO =6 см.	A		B
Оскільки за
			O
			O
Позначимо CO =x,	тоді DO =9−x. Маємо: x(9+x) =6 6,
x2 +9x−36 =0, x1 =3, x2 = −12 — не задовольняє умову задачі.
Отже, CO =3 см, CD =x+9+x =9+6 =15 см.
Довжина кола l = π CD =15π см.
Відповідь. 15π см.

62 ВАРІАНТ 21

Частина четверта

4.1.М За теоремою Вієта для коренів рівняння 2x2 −8x+3 =0 маємо:	x1 +x2 =4,
		x	x =	3	.


		1	2	2

x1 −x2 = (x1 −x2 )2 = x12 −2x1x2 +x22 = x12 +2x1x2 +x22 −4x1x2 =

= (x1 +x2 )2 −4x1x2 = 42 −4 32 = 16−6 = 10 .

Відповідь. 10 .

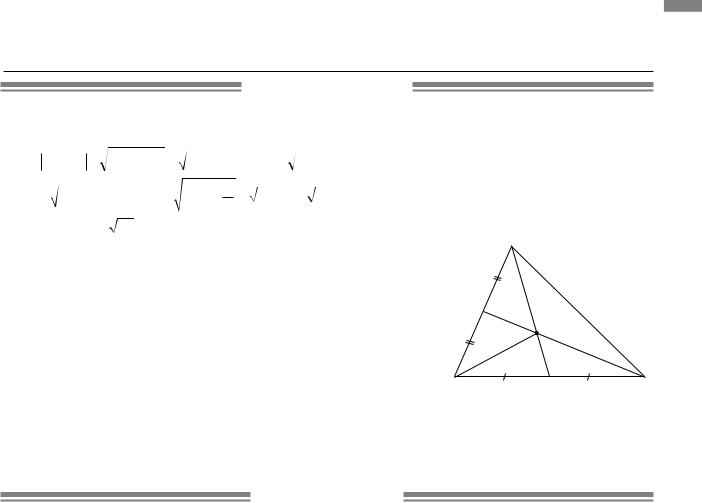
4.2.М На рисунку зображено трикутник ABC, BE і CF — медіани трикутника.

Сполучимо точки A і M.

Відомо: SAME = SEMC,		SAMF	=SMFB , SAMC =SAMB =SCMB.
Тоді SAFM =SAME =	1	SAMC	і SAFME =2SAME =SAMC =SCMB , що
	2

й треба було довести.

A E C

Варіант 21

Частина перша

1.1. (1865−365):50 =1500:50 =30.

Відповідь. В).

1.2.72 =2 2 2 3 3 =23 32 ; 48 =2 2 2 2 3=24 3. НСД =23 3 =24.

Відповідь. Г).

1.3.Відповідь. Б).

1.4.Оскільки 0 2−0 (−2) =0 ≠ 4, 0 2+2 (−2) = −4, 2 2+0 (−2) =4 ≠ −4, 2 2+2 (−2) =0 ≠8, то через подану точку проходить графік рівняння 0 x+2y = −4.

Відповідь. Б).

1.5.	2x	+	y	=	2x 4+y y	=	8x+y2	.
	y				4y
		4					4y

Відповідь. В).

1.6.Зведене квадратне рівняння має вигляд x2 + px+q =0. За теоремою, оберненою до теореми

Вієта −(x1 +x2 ) = p, x1 x2 =q. Отже, p = −(5+(−3)) = −2, q =5 (−3) = −15. Тоді рівняння має ви-

гляд: x2 −2x−15 =0.

Відповідь. Г).

1.7.Оскільки x−y =(−1)5 <0, то x < y.

Відповідь. А).

										ВАРІАНТ 21 63

	Sn =	b	(qn −1)		=	b	(33 −1)		=13b1 ,	b1 =4.
1.8.		1		. 52		1		, 52
1.8.			q −1	. 52			3−1	, 52
			q −1				3−1
	Відповідь. Б).
1.9.	Нехай AM =x см, тоді BM =3x см. За умовою x+3x =84, 4x =84, x =21.
	BM =3 21=63 см.

Відповідь. Г).

1.10.Нехай коефіцієнт пропорційності дорівнює k. Тоді довжини сторін дорівнюють 3k і 4k, а периметр паралелограма 2(3k+4k) =70, звідки k =5. Отже, сторони паралелограма дорівнюють

15 см, 15 см, 20 см, 20 см.

Відповідь. В).

1.11.Нехай невідома сторона трикутника дорівнює a дм. Тоді за теоремою косинусів

a2 =62 +82 −2 6 8 cos60°=36+64−2 48	1	=52, a = 52 =2 13 дм.
	2

Відповідь. Г).

1.12. 3a(−3;3), 2b(4;−6), c(−3−4:3−(−6)), c(−7;9).

Відповідь. Б).

Частина друга

2.1.	3 1	4	1	3	−	(−4)6 =3	13	16	−43 =3	4	−64 = −60.
		9		13			9	13		3

Відповідь. –60.

2.2.Оскільки вершина параболи розташована в початку координат, то формула, що задає відповідну функцію, має вигляд y =ax2. Враховуючи, що парабола проходить через точку A (2;−8), знаходимо коефіцієнт a: −8 =a 22 , a = −2.

Відповідь. y = −2x2 .

x−y =3,

x−y = −3,

2.3.

(x−y) =9,

звідки

звідки x =8, y =11.

−y =5,

x =2, y = −1, або

−y =5,

2x−y =5;

Відповідь.

(2;−1), (8;11) .

x° , тоді зовнішній —

x°

2.4.

Нехай внутрішній кут правильного многокутника дорівнює

Оскільки

сума

зовнішнього і

внутрішнього

кутів

дорівнює

180°,

то x+

=180, x =150.

Внутрішній

кут правильного

n -кутника

дорівнює

180(n −2)

тобто

180(n −2)

=150,

180n−360 =150n, 30n =360, n =12.

Відповідь. 12 сторін.

64 ВАРІАНТ 21

Частина третя

3.1.Нехай швидкість руху мотоцикліста x км/год. Систематизуємо дані у вигляді таблиці.

Рух

s, км

v, км/год

t, год

Мотоцикліст

Велосипедист

x−45

x −45

Враховуючи, що мотоцикліст був у дорозі на 3 год менше, ніж велосипедист, складаємо

рівняння:

−

=3. ОДЗ: x ≠45, x ≠0.

x −45

60x−60(x −45) −3x(x −45)

=0,

x2 −45x−900 =0, x1 =

−75

= −15

— не задовольняє

умову

x(x −45)

задачі,

x2 =

45+75

=60. Отже, швидкість руху мотоцикліста 60 км/год, а швидкість руху ве-

лосипедиста 60−45 =15 км/год.

Відповідь. 15 км/год.

3.2. Задана функція не визначена при x = −2 та x =0.

–2

(x +4)(x +2)

x(2−x)

y =

−

= x+4

−(2−x) =2x+2.

x +2

–2

Графік функції зображено на рисунку.

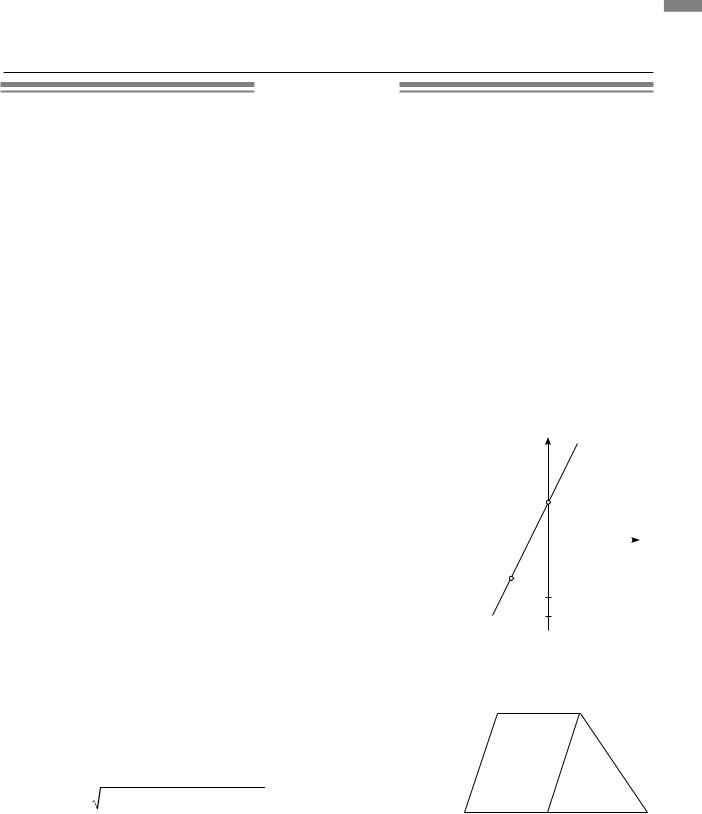
3.3.У трапеції ABCD основи BC =10 см і AD =14 см, бічні сторони AB =13см і CD =15 см. CN — висота трапеції. Проведемо CK AB.

ABCK — паралелограм, у нього CK = AB =13 см,

AK = BC =10 см. KD = AD− AK =14−10 =4 см.

Знаходимо площу трикутника CKD:

за формулою Герона. p =

13 + 15 + 4

=16

см,

S =

16(16−4)(16−13)(16−15) =24 см2;

2 24

K N

S =

KD CN. Маємо: CN =

=12 см.

Отже, SABCD =

BC + AD

CN =

10 +14

12 =144 см2.

Відповідь. 144 см2.

ВАРІАНТ 22 65

Частина четверта

4.1.М

4.2.М


	=13,
x+y+ xy
x2 +xy+y2 =91.

Нехай x+ y = a,		xy =b, тоді x2 +2xy+y2 =a2			і x2 +xy+y2 =a2 −b2 і система рівнянь набуває
вигляду:			a+b =13,		=13,
вигляду:	a+b =13,			a+b	=13,	a =10,
	a2 −b2	=91;	(a−b)(a+b) =91;	a−b =7;		b =3.
x+y =10,
Отже,		x+y =10,
	xy =3;	xy =9.

За теоремою, оберненою до теореми Вієта, маємо:						x =1,	x =9,
За теоремою, оберненою до теореми Вієта, маємо:							або
						y =9	y =1.
Відповідь. (1;9), (9;1).
Знайдемо відстань від точки O(1;−2) до прямої 3x−4y+9=0:
ρ=	3 1−4 (−2) +9		=	20	=4.


	32 +(−4)2
	32 +(−4)2	5

Оскільки коло дотикається до прямої 3x−4y+9=0, то радіус кола дорівнює відстані від центра кола до прямої, тобто R =4.

Рівняння кола з центром O(1;−2) і R =4 має вигляд: (x−1)2 +(y+2)2 =16.

Відповідь. (x−1)2 +(y+2)2 =16.

Варіант 22

Частина перша

1.1.16 кг 300 г – 8 кг 500 г = 15 кг 1300 г – 8 кг 500 г = 7 кг 800 г.

Відповідь. Г).

1.2.13 + 71 = 721+3 = 1021 .

Відповідь. В).

1.3.2a(b−3c) =2ab−6bc.

Відповідь. Г).

1.4.Прямі, що є графіками лінійних функцій y = kx+ b паралельні, якщо кутові коефіцієнти k рівні між собою. Оскільки 1≠2, 2 =2 , −2 ≠2 , −5 ≠2 , графіку функції y =2x−5 паралельна пряма y =10+2x .

Відповідь. Б).

1.5.	9	2x2	=	9 2x2	=	3 2	=	6	.
	x3			x3 3		x
		3						x

Відповідь. А).

66		ВАРІАНТ 22

1.6.		( 3 −2)2 + 48 =( 3 )2 −2 2 3 +22 + 16 3 =3−4 3 +4+4 3 =7.

Відповідь. В).

1.7.Ордината точки перетину графіка функції з віссю абсцис дорівнює нулю. Тому −5x+15 =0,

−5x = −15, x =3.

Відповідь. Б).

1.8. 30024 100%=8%.

Відповідь. А)

1.9. POS = POQ+ SOQ. Кути POQ і KOM вертикальні, тому POQ = KOM =130°. Отже,

POS =100°+30°=130°.

Відповідь. Б).

1.10.Нехай гострий кут трапеції дорівнює x° , тоді тупий — дорівнює 3x°. Оскільки сума гострого і тупого кутів прямокутної трапеції дорівнює 180°, x+3x =180°, x =45 °, 3x =3 45 =135.

Відповідь. А).

1.11. Другий катет прямокутного трикутника дорівнює 52 −42 =3 дм. Тоді площа прямокутного трикутника S = 12 3 4 =6 дм2.

Відповідь. В).

1.12.Нехай B(x;y). Тоді 1= −32+ x , x =5; −3 = −22+ y , y = −4.

Відповідь. Г).

Частина друга

2.1.x2 (x+2) −(x+2) =0, (x+2)(x2 −1) =0, (x+2)(x−1)(x+1) =0, x1 = −2, x2 =1, x3 = −1.

Відповідь. −2; −1; 1.

2.2.За умовою y =2x. Тоді 2x =10−3x, 5x =10, x =2, y =2 2 =4.

Відповідь. (2;4).

2.3. Відомо, що b4 =b2q2 . Тоді q2 =b4													:b2 =		1	:	1		=	1	, q =	1	. b1 =b2 :q =	1	:	1	=	1	.
2.3. Відомо, що b4 =b2q2 . Тоді q2 =b4													:b2 =			:	2		=	2	, q =	2	. b1 =b2 :q =	2	:	2	=		.
				1					7				4				2			2		2		2		2	2
				1		1			7	−
	b (qn −1)										1
											1
				2			2							15+7		2
	1													15+7		2		.
Sn = q −1 =						1		−1				=	8 2					.
Sn = q −1 =						1						=	8 2
						2
						2
Відповідь.		15+7		2	.
Відповідь.			8 2		.

2.4.Нехайкоефіцієнтпропорційностідорівнює k.Тодідовжинидвохсторінтрикутникадорівнюють

5k см і 3k см. Довжину a третьої сторони знайдемо за теоремою косинусів, урахувавши, що

cos120°= − 12 : a2 =(3k)2 +(5k)2 −2 3k 5k cos120°=9k2 +25k2 +15k2 =49k2 , a =7k см. За умовою

3k+5k+7k =45, k =3. Тоді довжина третьої сторони трикутника дорівнює 7 3 =21 см.

Відповідь. 21 см.

ВАРІАНТ 22 67

Частина третя

3.1.Нехай перша труба може наповнити басейн за x год, тоді друга труба може його спорожни-

ти за (x+3)

год. За одну годину перша труба наповнює

частину басейну, а друга труба

спорожнює

частину басейну. Враховуючи, що за одночасної роботи труб басейн напо-

x +3

вниться за 36 год, складаємо рівняння:

−

. ОДЗ: x ≠ −3, x ≠0.

x +

36(x +3) −36x −x(x +3)

=0, x2 +3x−108 =0, x1 =

−3

−21

= −12

— не задовольняє умову задачі,

x(x +3)

x2 =

−3+21

=9.

Отже,

труба

може наповнити басейн за

год,

а друга — його

спорожнити

перша

за 9+ 3 = 12 год.

Відповідь. 9 год, 12 год.

−4x+3 при x 0,

3.2. y = x

x2 +4x+3 при x <0.

Будуємо графік функції y =x

−4x+3 на проміжку

+ ∞).

Графіком є парабола, вітки якої напрямлені вгору. Абсциса

вершини параболи m = 2 =2.

y(2) = −1. Отже, вершина параболи — точка (2;−1). Абсциси

–2

точок перетину графіка з віссю Ox x1 = 1, x2 = 3.

На проміжку (−∞;0)

будуємо графік функції y = x2 +4x+3.

–1

3 x

m = −

= −2, y(−2) = −1. Він перетинає вісь Ox у точках з аб-

сцисами –1 і –3.

3.3.Знаходимо сторони чотирикутника ABCD.

AB = (xB −xA )2 +(yB −yA )2 = (5−0)2 +(7−6)2 = 26 ,

BC =	(xC −xB )2 +(yC −yB )2 = (4−5)2 +(2−7)2 = 26 ,
CD =	(xD −xC )2 +(yD −yC )2 = (−1−4)2 +(1−2)2 = 26 ,

AD = (xD −xA )2 +(yD −yA )2 = (−1−0)2 +(1−6)2 = 26 .

Знаходимо координати середин діагоналей.

AC: x =

xA + xC

0 +4

=2,

y =

+ yC

6 +2

=4; точка

(2;4) .

BD:

x =

xB + xD

5−1

=2;

y =

+ yD

7 +1

, точка

(2;4) .

У чотирикутника ABCD сторони рівні, діагоналі перетинаються і точкою перетину діляться навпіл, отже, чотирикутник ABCD є ромбом.

68 ВАРІАНТ 22

Частина четверта

−xy+y

) =19,

(x+y)(x

4.1.М Запишемо систему рівнянь у вигляді

(xy+8)(x+y) =2.

Нехай x+ y = a, xy = b, тоді x2 +y2 =(x+y)2 −2xy =a2 −2b і система набуде вигляду:

a(a−3b) =19,

(b+8)a =2.

Поділивши перше рівняння системи на друге, маємо:

a −3b

, a =

25b+152

=12, 5b+76.

b +8 2

Підставимо здобуте значення у друге рівняння системи:

(b+8)(12,5b+76) =2, 12,5b2 +176b+606 =0,

звідки b1 = −6 або b2 = −8,08.

a =1,

a = −25,

x+y =1,

x+y = −25,

Маємо:

або

Отже,

або

b = −6

b = −8,08.

xy = −6

xy = −8,08.

Розв’язавши першу систему рівнянь, дістанемо: (−2;3), (3;−2) .

Розв’язки другої системи рівнянь:

−25−	657,32		−25+ 657,32		−25+	657,32		−25− 657,32
		;		,			;		.
		;		,			;		.
	2		2			2		2
	2		2			2		2

	−25−	657,32		−25+	657,32		−25+	657,32		−25−	657,32
Відповідь. (−2;3), (3;−2) ,			;			,			;			.

		2			2			2			2

4.2.М Нехай у

трикутнику ABC:

AB = AC,

BAC = BCA =72°,

AK — бісектриса, AK =l.

Оскільки BAC = ACB =72°, то ABC =36°.

Отже, трикутник

ABK

рівнобедрений

з основою

і BK = AK =l.

36°

Оскільки

AK — бісектриса кута

A, то CAK = KAB=36°

і трикутник

CAK

рівнобедрений

основою KC,

тобто

AC = AK =l.

ABC CAK за двома кутами, отже,

Нехай CK =x, тоді AB = BC =l+x,

l + x

72°

36°

−l +l 5

( 5

−1).

72°

звідки x

+lx−l

=0, x =

36°

l(1+

5 )

Отже, BC =l+

(

5 −1) =

Відповідь. l,

(

5 +1).

ВАРІАНТ 23 69

Варіант 23

Частина перша

1.1.x =910 65, x =59150.

Відповідь. Б).

1.2.5 53 10 = 285 10 = 28510 =56.


	Відповідь. Г).
1.3.	(3a−b)2 =(3a)2 −2 3a b+b2 =9a2 −6ab+b2 .
	Відповідь. Б).
1.4. 3m+mk−3n−kn =(3mk+mk) −(3n+kn) =m(3+k) −n(3+k) =(3+k)(m−n).
	Відповідь. А).
1.5.		a8 (a2 )−3		=	a8 a−6				=a8+(−6)−7 =a−5 .
		a7
						a7
	Відповідь. Б).
		a2 −b2		3a			(a −b)(a +b) (−3a)
1.6.						=				= −3.
		a2 + ab	b −a					a(a +b) (a −b)
	Відповідь. Г).
1.7.	Оскільки −(−2)2 −2 (−2) +3 =3 >0, (−2)2 −6 (−2) +8 =24 >0, 2 (−2)2 −3 (−2) +1=15 >0,
	(−2)2 +5 (−2) −7 = −13<0, то число −2 є розв’язком нерівності 2x2 −3x+1>0.

Відповідь. В).

1.8.На рисунку зображено графік функції y = −(x−1)2 +4 = −x2 +2x+3.

Оскільки −(x−1)(x+3) = −x2 −2x+3 ≠ −x2 +2x+3; (x−1)(x+3) =x2 +2x−3 ≠ −x2 +2x+3;

(x+1)(x−3) =x2 −2x−3 ≠ −x2 +2x+3;

−(x+1)(x−3) = −x2 +2x+3, то функцію, графік якої зображено на рисунку, задає формула y = −(x+1)(x−3).

Відповідь. Г).

1.9.Шуканий кут є внутрішнім одностороннім з кутом 30°. Оскільки прямі a i b паралельні, x+3 =180, x =150.

Відповідь. Г).

1.10. Оскільки суми протилежних сторін чотирикутника, описаного навколо кола, рівні,

то AB+CD = AD+ BC, 7+CD =9+8, CD =10 см.

Відповідь. В).

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015227.84 Кб3Doc1.doc
#
14.02.2015224.77 Кб2Doc2.doc
#
04.09.2019706.05 Кб1Dodatok_1.doc
#
15.02.201540.84 Кб4Dokument_Microsoft_Office_Word.docx
#
12.03.201615.72 Mб166dopatka_r_perepechko_a_kniga_o_sudah.pdf
#
15.02.20152.63 Mб44DPA_2011_mat-9-rozvyazannya-vsx-zavdan.pdf
#
06.11.2018148.48 Кб1dvp_pr_001.doc
#
14.02.2015318.98 Кб9Ekonomichna_istoriya_Ukrayini.doc
#
01.05.2025126.07 Кб0Ekonomichna_istoriya_Ukrayini.docx
#
15.02.201556.71 Кб30ekonomika.docx
#
15.02.20151.71 Mб305Ekon_Pidp_ta_mij-komp-Fedorova.pdf