
DPA_2011_mat-9-rozvyazannya-vsx-zavdan
.pdf

НОВЕ, ВИПРАВЛЕНЕ ТА ДОПОВНЕНЕнове виданняВИДАННЯ
Математика
Розв’язання всіх завдань
до збірника завдань для державної підсумкової атестації з математики (Істер О. С., Глобін О. І., Комаренко О. В.)
1

УДК 51(076.2) ББК 74.262.21 М34
М34 Математика. 9 клас: Розв’язання всіх завдань для державної підсумкової атестації / Упоряд. В. С. Кулік.— Х.: Ранок-НТ, 2011.— 112 с.
ISBN 978-966-315-112-0
Посібник допоможе успішно підготуватися до державної підсумкової атестації з математики, а також заощадити час на підготовку. Він містить розв’язання всіх завдань із навчального посібника «Збірник завдань для державної підсумкової атестації з математики. 9 клас» (авт. Істер О. С., Глобін О. І., Комаренко О. В.— К.: Освіта, 2011).
Посібник побудовано за таким принципом. Спочатку, відповідно до збірника завдань, вказано номер варіанта атестаційної роботи, її частина (перша—четверта), номер завдання, а потім подано розв’я зання завдання і відповідь до нього.
У кінці посібника наведено правильно заповнені бланки відповідей для першої та другої частин кожного варіанта атестаційної роботи.
Посібник призначений для учнів загальноосвітніх навчальних закладів і вчителів.
УДК 51(076.2) ББК 74.262.21
|
© |
В. С. Кулік, упорядкування, 2011 |
ISBN 978-966-315-112-0 |
© |
ПП «Ранок-НТ», 2011 |
2
3
Варіант 1
Частина перша
1.1.56+42:14−7 =56+3−7 =52.
Відповідь. В).
1.2.12 =2 2 3 =22 3; 16 =2 2 2 2 =24 . Тому НСК (12;16) =24 3 =16 3 =48.
Відповідь. А).
1.3.Відповідь. Б).
1.4.Додавши почленно рівняння системи, дістанемо 5x−y =3, y =5x−3. Тоді з другого рівняння
системи: 3x+2(5x−3) =7, 3x+10x−6 =7, 13x =13, x =1; y =5 1−3 =2. Розв’язком системи
рівнянь є пара чисел (1;2) .
Відповідь. Г).
1.5.10x3y = 2x2 .
15y2x 3y
Відповідь. А).
1.6. За теоремою |
Вієта сума коренів рівняння x2 + px+q =0 дорівнює −p. Сума коренів рівняння |
x2 +9x−5 =0 |
дорівнює –9. |
Відповідь. В).
1.7.Відповідь. Б).
1.8. S = |
b1 |
, b1 = −6, b2 =1, q = |
b2 |
= − |
1 |
, S = |
−6 |
|
|
= −5 |
1 |
. |
||
1−q |
b1 |
|
|
|
|
1 |
|
|||||||
|
|
6 |
|
|
|
7 |
|
|||||||
|
|
|
1− |
− |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
Відповідь. Г).
1.9.Відповідь. Б).
1.10.Кути BOC і COD суміжні, BOC =180°−50°=130°.
Трикутник BOC рівнобедрений, тому
CBO = BCO =(180°−130°):2 =25°.
Відповідь. А).
BС
O
AD
1.11. За теоремою косинусів |
AC2 = AB2 +BC2 −2 AB BC cosB. Враховуючи, що cos60°= |
1 |
, |
|||
2 |
||||||
|
1 |
|
|
|
||
AC2 =52 +32 −2 5 3 |
=19, |
AC = 19 см. |
|
|
||
|
|
|
||||
2
Відповідь. Г).
1.12. a b =2x+(−2) 5 =10, якщо x =10.
Відповідь. В).
4 |
ВАРІАНТ 1 |
|
|
|
|
|
|
Частина друга |
2.1. |
( 5 −2 3 )2 + 240 =( 5 )2 −2 5 2 3 +(2 3 )2 + 16 15 =5−4 15 +12+4 15 =17. |
|
|
|
Відповідь. 17. |
2.2.Нехай y = −x. Тоді −x =x2 +3x−5, x2 +4x−5 =0, x1 =1, x2 = −5; y1 = −1, y2 =5.
Відповідь. (1;−1), (−5;5).
2.3.З першого рівняння системи: x =3−3y. Підставивши значення x у друге рівняння системи,
дістанемо y2 −(3−3y)y =7, y2 −3y+3y2 =7, 4y2 −3y−7 =0, y1 = −1, y2 =1,75.Тоді x1 =3−3 (−1) =6, x2 =3−3 1,75 = −2,25.
Відповідь. (6;−1), (−2,25;1,75).
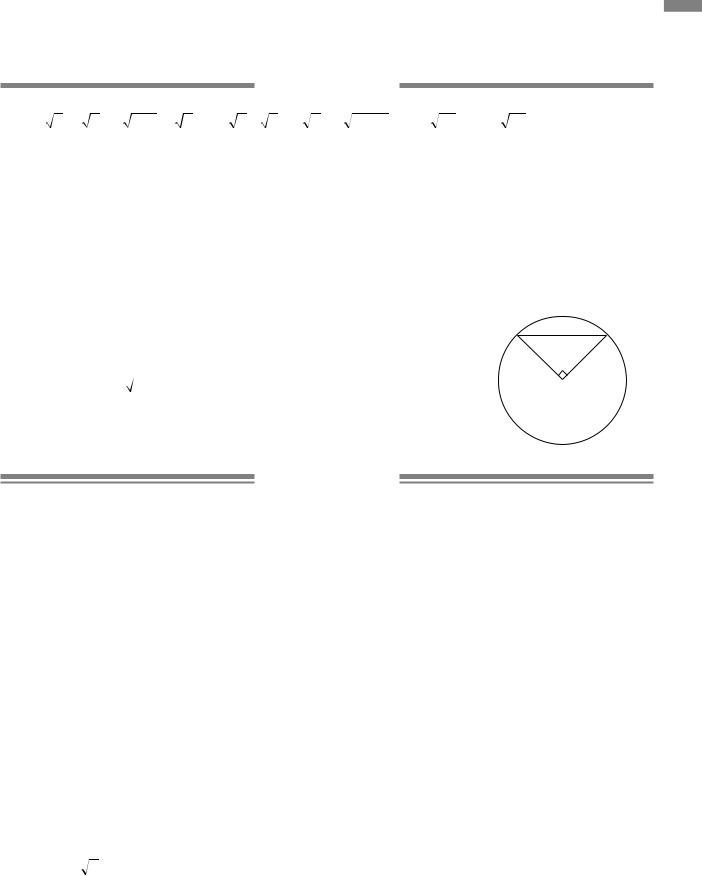
2.4. Оскільки AB =90°, то AOB =90°. Трикутник AOB |
A |
B |
||||
|
|
|||||
прямокутний рівнобедрений, AO = BO = R, AB2 =2R2, |
|
|
||||
R2 = |
AB2 |
= |
(8 2 )2 |
=64, R =8, C =2πR =2π 8 =16π см. |
|
O |
|
|
|
|
|||
2 |
2 |
|
|
|
||
Відповідь. 16π см.
Частина третя
3.1.Нехай x км/год — швидкість руху поїзда за розкладом. Систематизуємо дані у вигляді таблиці.
|
|
|
|
Рух |
|
|
|
|
|
|
s, км |
|
|
|
|
|
v, км /год |
|
|
|
t, год |
||||||
|
|
За розкладом |
|
180 |
|
|
|
|
|
|
x |
|
|
|
180 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Після збільшення |
|
180 |
|
|
|
|
|
|
x+5 |
|
|
|
|
180 |
|
|
||||||||||
|
|
|
швидкості |
|
|
|
|
|
|
|
|
|
|
|
|
x+5 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Оскільки |
|
180 |
|
на 24 |
хв = |
|
24 |
|
год = |
2 |
год менше за |
180 |
, |
то маємо рівняння: |
||||||||||
|
|
|
x+5 |
|
60 |
|
5 |
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
180 |
|
− |
180 |
= |
2 |
|
. ОДЗ: x ≠0, |
x ≠ −5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x+5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Розв’яжемо отримане |
рівняння: |
5 180(x+5) −5 180x =2x(x+5); |
2x2 +10x−4500 =0; |
|||||||||||||||||||||
x2 +5x−2250 =0; x1 =45, x2 = −50. Другий корінь не задовольняє умову задачі. Отже, швидкість руху поїзда за розкладом 45 км/год.
Відповідь. 45 км/год.
3.2.ОДЗ: x >0.
1 |
− |
1 |
=0 або x2 −3x =0. З першого рівняння x =4, з другого рівняння x =0 або x =3. |
|
x |
2 |
|||
|
|
Значення x =0 не входить в ОДЗ.
Відповідь. 3; 4.
ВАРІАНТ 2 5
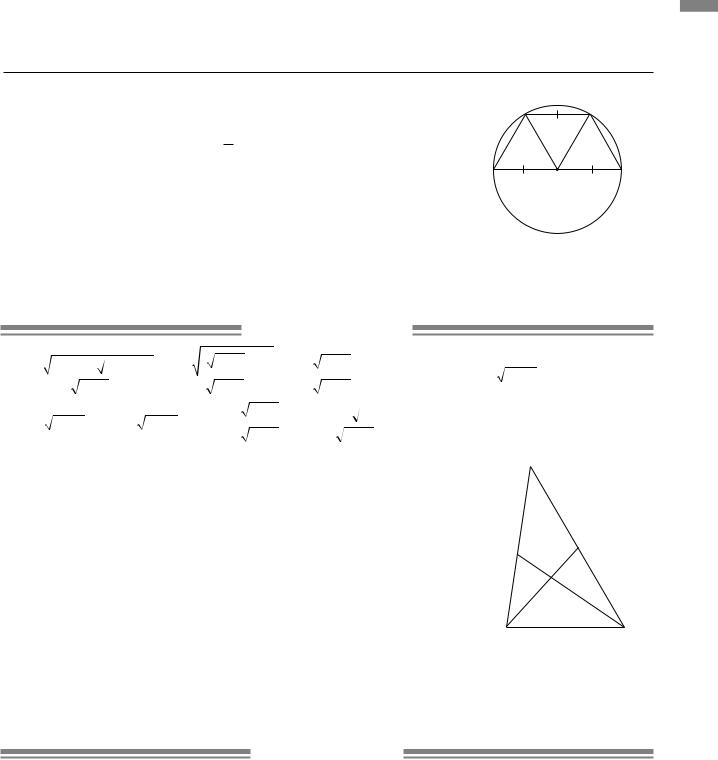
3.3.На рисунку зображено коло, описане навколо трапеції ABCD.
За умовою центр кола — точка О належить основі AD трапеції. |
B |
|
С |
|
AO = DO = BO =CO як радіуси одного кола. Оскільки за умо |
|
|||
|
|
|
||
вою BC: AD =1:2, то BC = 1 AD. Тоді трикутник |
BOC рів |
|
|
|
2 |
|
|
|
|
носторонній, кожен з його кутів дорівнює 60°. |
|
A |
O |
D |
Трикутники COD і BOA — рівнобедрені з основами CD |
|
|
||
|
|
|
||
і BA відповідно. ODC = OCD. ODC+ OCD+ BCO =180°, |
|
|
|
|
ODC = OCD =(180°−60°):2 =60°. |
|
|
|
|
Отже, DCB =180°− ODC =180°−60°=120°. |
|
|
|
|
OAB =60°; ABC =120°. |
|
|
|
|
Відповідь. 60°; 120°. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частина четверта |
|||||||||||||
4.1.м |
m−2−2 m−2 +1 |
+1= |
|
( m−2 −1)2 |
|
+1= |
|
|
m−2 −1 |
|
|
+1. При m =2,98 |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
m−2 −1 |
|
m−2 −1 |
|
|
|
|
|
|
|
m−2 −1 |
||||||||||||
|
m−2 −1 |
|
=1− m−2 . Отже, |
|
|
m−2 −1 |
|
+1= |
1− m−2 |
+1= −1+1=0. |
|||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
m−2 −1 |
|
|
|
m−2 −1 |
|||||||||
Відповідь. 0. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4.2.м У трикутнику ABC сторона |
|
AC =10 см, точка O — точка |
|||||||||||||||||||||
перетину медіан AD і CF, проведених до сторін BC і AB |
|||||||||||||||||||||||
відповідно. AD =9 см, CF =12 см. Оскільки медіани трикут- |
|||||||||||||||||||||||
ника точкою перетину діляться у відношенні 2 : 1 (рахуючи |
|||||||||||||||||||||||
від вершини), то AO =6 |
см, CO =8 |
см. Трикутник AOC пря- |
|||||||||||||||||||||
мокутний, оскільки AC2 = AO2 +CO2 |
(100 =36+64). |
|
|||||||||||||||||||||
|
Його площа SAOC = |
1 |
AO CO = |
1 |
|
6 8 =24 см2. |
|||||||||||||||||
|
2 |
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отже, SABC =3SAOB =3 24 =72 см2.
Відповідь. 72 см 2.
m−2 −1<0, тому
B
F D
O 
AС
Варіант 2
Частина перша
1.1.16 год 26 хв = 15 год 86 хв; 16 год 26 хв – 9 год 52 хв = 15 год 86 хв – 9 год 52 хв = 6 год 34 хв.
Відповідь. Б).
1.2. |
3 |
+ |
1 |
= |
3 3+1 2 |
= |
11 |
. |
|
4 |
6 |
12 |
12 |
||||||
|
|
|
|
|
Відповідь. Г).
1.3.Відповідь. А).
1.4.Відповідь. Б).

6 ВАРІАНТ 2
1.5.a2 : a3 = a2 8 = 4 .
2 8 2 a3 a
Відповідь. В).
1.6. ( 5 − 3 )2 +2 15 =( 5 )2 −2 5 3 +( 3 )2 +2 15 = 5−2 15 +3+2 15 =8.
Відповідь. А).
1.7.Для того щоб дістати графік функції y =(x+3)2 , треба графік функції y =x2 перенести вздовж осі Ox на три одиниці ліворуч.
Відповідь. В).
1.8.P( A) = mn , де m — кількість елементарних подій, сприятливих події A, n — кількість усіх
можливих елементарних подій даного випадкового експерименту. m =3 (може випасти 2, 4 або 6 очок), n =6, оскільки кубик має шість граней. P( A) = 63 = 12 .
Відповідь. Б).
1.9.Градусна міра кута A дорівнює 50°. Тоді градусна міра кута, суміжного з кутом A, дорівнює
180°−50°=130°.
Відповідь. В).
1.10.У рівнобічної трапеції кути при основі рівні, а сума кутів при бічній стороні дорівнює 180°, тому з-поміж наведених величин кути трапеції можуть дорівнювати 70° і 110°.
Відповідь. Г).
1.11. S = |
1 |
AB BC sinB. Враховуючи, що sin120°= |
3 |
, |
S = |
1 |
3 |
6 |
3 |
= |
9 |
3 |
см2. |
|
|
2 |
|
2 |
|
2 |
|||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|||||
Відповідь. А). |
|
|
|
|
|
|
|
|
|
|
|
|
||
1.12. Рівняння кола має вигляд |
(x−a)2 +(y−b)2 = R2, де |
(a;b) |
— координати центра кола, R — |
|||||||||||
його радіус. Оскільки коло проходить через точку K(−1;5), то (−1+3)2 +(5−1)2 =20 = R2. Отже, |
||||||||||||||
рівняння заданого кола: (x+3)2 +(y−1)2 =20. |
|
|
|
|
|
|
|
|
|
|
|
|||
Відповідь. Б). |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Частина друга |
|
|
|
|
|
|
|||||
2.1. ОДЗ: x ≠ −2. x4 −x2 −12 =0. Нехай x2 =t. Тоді t2 −t−12 =0, |
t1 = −3, t2 =4. Рівняння x2 = −3 |
|||||||||||||
не має розв’язків. x2 =4, x1 = −2 (не належить ОДЗ), x2 =2. |
|
|
|
|
|
|||||||||
Відповідь. 2.
2.2.За умовою x =2y. Тоді y =12−1,5 2y, y =12−3y, 4y =12, y =3. x =2 3 =6.
Відповідь. (6;3).
2.3. S20 = a1 +2a2 n. Із співвідношення a10 =a5 +5d знаходимо d. 29=14+5d, d =3. Із співвідношення
a5 =a1 +4d знаходимо a1: a1 =a5 −4d =14−4 3 =2.
Тоді a20 =a1 +19d =2+19 3 =59. S20 = 2+259 20 =610.
Відповідь. 610.

ВАРІАНТ 2 7
2.4.Із сторін завдовжки 6 2 см і 10 см більшою є сторона, довжина якої 10 см. Нехай третя сто-
рона трикутника a см.
Тоді за теоремою косинусів 102 =a2 +(6 2 )2 −2a 6 2 cos45°, 100 =a2 +72−2a 6 2 22 , a2 −12a−28 =0, a1 = −2 (не підходить за змістом задачі), a2 =14.
Відповідь. 14 см.
Частина третя
3.1.Нехай x — кількість днів, за які друга бригада може зорати поле, працюючи окремо, а y —
кількість днів, необхідних першій бригаді для самостійного виконання роботи. Оскільки другій бригаді потрібно на це на 5 днів менше, ніж першій, то дістанемо рівняння y =x+5.
Друга бригада за 1 день виконує x1 , а перша бригада — 1y частину роботи. Отже, працюючи
разом, бригади виконають за 1 день x1 + 1y = 16 всієї роботи.
|
|
|
|
|
|
|
|
=x+5, |
|
(1) |
|||||
Дістанемо систему |
y |
|
|||||||||||||
1 |
|
+ |
1 |
= |
1 |
. |
(2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
y |
6 |
|||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||
Підставимо (1) в (2) і розв’яжемо отримане рівняння. |
|||||||||||||||
|
1 |
+ |
1 |
= |
1 |
. ОДЗ: x ≠ −5, x ≠0. |
|||||||||
|
x+5 |
|
|||||||||||||
|
x |
6 |
|
|
|
|
|
|
|
|
|
|
|||
|
6(x+5) +6x−x(x+5) |
=0, x2 −7x−30 =0, x1 = −3 — не задовольняє умову задачі, x2 =10. |
|||||||||||||
6x(x+5)
Отже, друга бригада може зорати поле за 10 днів, а перша — за 10+5 =15 днів.
Відповідь. 15 днів, 10 днів.
3.2.Перетворимо ліву частину заданої рівності. ((a+c) +b)((a+c) −b) =(a+c)2 −b2 = a2 +2ac+c2 −b2.
Тоді задана рівність набуває вигляду a2 +2ac+c2 −b2 =a2 +b2 +c2; ac =b2. Отримана рівність виконується, якщо a, b, c — послідовні члени геометричної прогресії.
3.3.За властивістю діагоналей паралелограма
BO = |
1 |
BD = |
1 |
8 =4 см, AO = |
1 |
|
AC = |
1 |
10 =5 см. |
|
|
B |
С |
|||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
O |
||||||
|
З прямокутного трикутника AOB ( B =90°): |
|
|
|||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
AB |
3 |
|
A |
D |
|
AB= |
AO |
|
−BO |
|
= 25−16 =3 см; sin AOB = |
|
= |
|
. |
|
|
|||||||||||||
|
|
AO |
5 |
|
|
|||||||||||||||||||
|
Площа паралелограма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
S = |
|
1 |
|
AC BD sin AOB = |
1 |
8 10 |
3 |
=24 см2. |
|
|
|
|
|||||||||||
|
|
2 |
|
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||||||
Відповідь. 24 см 2.
8 |
ВАРІАНТ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Частина четверта |
|
|
|
|
|
|
|
|
|||
4.1.М Рівняння |
x2 |
− 4ax+ 3a2 − 2a−1 |
|
|
|
|
2 |
−4ax+3a |
2 |
−2a−1=0, |
|
|
||||||||
|
|
|
|
|
=0 рівносильне системі x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x− 4 |
|
|
|
|
x ≠ 4. |
|
|
|
|
|
|
||
|
Розв’язуючи рівняння системи, маємо: |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
D |
=4a2 −3a2 |
+2a+1=a2 +2a+1=(a+1)2; x1 =2a+a+1=3a+1; x2 =2a−a−1=a−1. |
|
|
|||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рівняння, що задано в умові, має єдиний корінь в одному з таких випадків: |
|
|
|||||||||||||||||
|
1) x1 =x2 і x1 ≠4; |
2) x1 =4, x2 ≠4; |
|
3) x1 =4, x2 =4. |
|
|
|
|
|
|
||||||||||
|
Розглянемо ці випадки. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1) |
3a+1= a−1; a = −1. У цьому випадку x1 = −2. |
|
|
|
|
|
|
|
|
||||||||||
|
|
Отже, |
a = −1 задовольняє умову задачі. |
|
|
|
|
|
|
|
|
|
||||||||
|
2) |
3a+1=4, |
|
a =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
≠4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3) |
a−1 |
=4, |
|
a =5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
≠4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3a+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Відповідь. a = −1; a =1; a =5. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
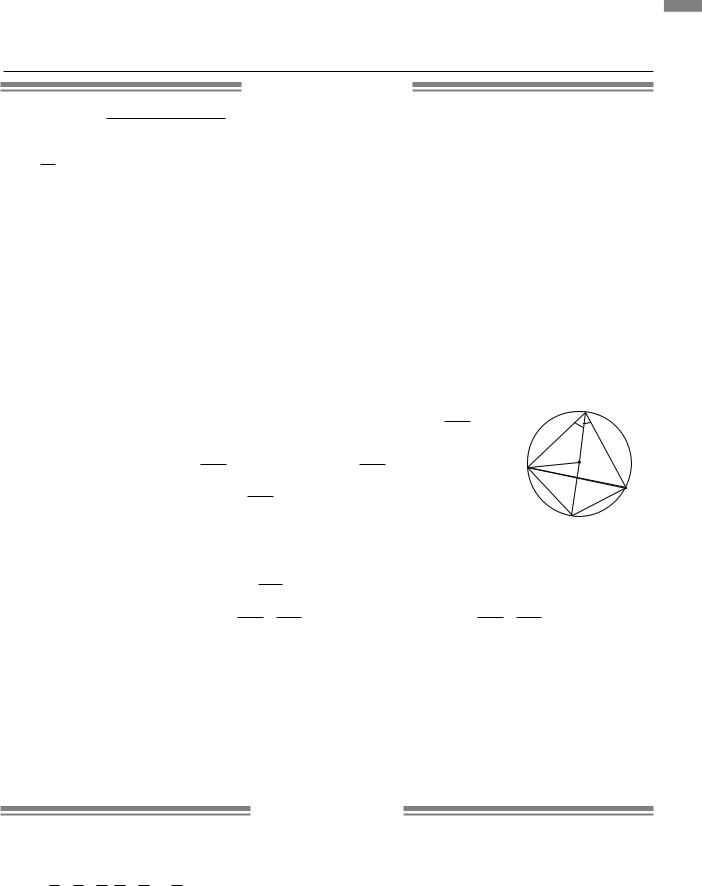
4.2.М На рисунку зображено коло і вписаний у нього трикутник |
ABC. |
|
|
|
|
|||||||||||||||
|
AK — бісектриса кута |
A, що перетинає коло у точці K. |
A . |
|
|
|
A |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Оскільки AK — бісектриса кута A, то BAK = KAC = |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
За властивістю вписаних кутів, що спираються на одну дугу, |
|
|
|
|
||||||||||||||
|
маємо: CBK = KAC = A |
і KCB = KAB = A . |
|
|
|
|
|
B |
|
I |
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
Отже, |
|
|
CBK = KCB = 2 |
, |
тобто |
трикутник |
CKB |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
рівнобедрений з основою BC, звідки KB = KC. |
|
|
|
|
|
|
K |
|
|||||||||||
|
|
Оскільки точка I — центр вписаного в трикутник кола, тобто |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
точка перетину бісектрис трикутника |
ABC, то BI — бісектриса |
|
|
|
|
||||||||||||||
|
кута CBA. Отже, CBI = IBA = B . |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
KBI = KBC+ CBI = A + |
B |
; KIB = IBA+ BAI = |
A |
+ B |
як |
зовнішній |
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
для трикутника IBA. Маємо: KBI = KIB, тобто трикутник KBI — рівнобедрений з осно- |
|||||||||||||||||||
|
вою BI, отже, |
KB = KI. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Дістали: |
|
KB = KC = KI, що й треба було довести. |
|
|
|
|
|
|
|
|
||||||||
Варіант 3
Частина перша
1.1.Оскільки 4 3−5 =7, 4 12−5 =43 ≠7, 4 14−5 =51≠7, то коренем рівняння є число 3.
Відповідь. А).
1.2.2 12 1 52 = 52 75 = 72 =3 12 .
Відповідь. В).

ВАРІАНТ 3 9
1.3. (x+2y)2 =x2 +2 x 2y+(2y2 ) = x2 +4xy+4y2.
Відповідь. Г).
1.4.−2x(2y−3x) −4x(2x−y) = −4xy+6x2 −8x2 +4xy = −2x2 .
Відповідь. Б).
1.5.80 2−3 −22 = 8023 −22 = 808 −4 =10−4 =6.
Відповідь. Г).
1.6. |
|
x2 −1 |
: |
x+1 |
= |
(x−1)(x+1) |
|
x2 |
= |
x(x−1) |
. |
|
|
|
5x |
x+1 |
|
||||||
|
|
5x |
x2 |
|
5 |
|
|||||
|
Відповідь. В). |
|
|
|
|
|
|||||
1.7. |
Оскільки 3 12 +6 1=9>0; 12 −4 1+4 =1>0; −3 12 −6 1= −9<0, то число 1 є розв’язком нерів |
||||||||||
|
ності −3x2 −6x 0. |
|
|
|
|
|
|||||
Відповідь. Г).
1.8.Вершина параболи y =x2 +1 має координати (0;1); вершина параболи y =(x+1)2 має координати (−1;0); вершина параболи y =x2 −1 має координати (0;−1); вершина параболи y =(x−1)2 +1 має координати (1;1).
Тобто осі абсцис належить вершина параболи y =(x+1)2.
Відповідь. Б).
1.9.За ознакою паралельності прямих, прямі паралельні, якщо відповідні кути рівні. Отже, градусна міра кута x має дорівнювати 75°.
Відповідь. Г).
1.10. Трикутники MON і KOP подібні (за двома кутами), |
M |
|
N |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
||||||||||||
отже, NO:OP = MN:PK = 4:6 = 2:3. |
|
|
|
|
|
|
O |
|||||||||
Відповідь. А). |
|
|
|
|
|
|
|
|
|
|
||||||
1.11. l = |
πRn |
= |
π 3 60 |
= π (см). |
|
|
|
|
|
P |
|
|
|
K |
||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
180 |
180 |
|
|
|
|
|
|
|
|
|
|
|
||||
Відповідь. В) |
|
|
|
|
|
|
|
|
|
|
||||||
1.12. S = |
1 |
AB BC sinB, звідки sinB = |
2S |
= |
2 20 3 |
= |
3 |
, B =60°. |
|
|
|
|||||
|
AB BC |
8 10 |
2 |
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Відповідь. Г).
Частина друга
2.1. |
x−3 |
− |
3−y |
|
xy−x2 |
xy−y2 |
|||
|
|
Відповідь. − xy3
|
x−3 |
|
3−y |
|
y(x−3) +x(3−y) |
|
xy−3y+3x−xy |
|
3(x−y) |
3 |
|
|
= |
|
− |
|
= |
|
= |
|
= |
|
= − |
|
. |
x(y−x) |
y(x−y) |
xy(y−x) |
xy(y−x) |
xy(y−x) |
xy |
|||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
