
DPA_2011_mat-9-rozvyazannya-vsx-zavdan
.pdf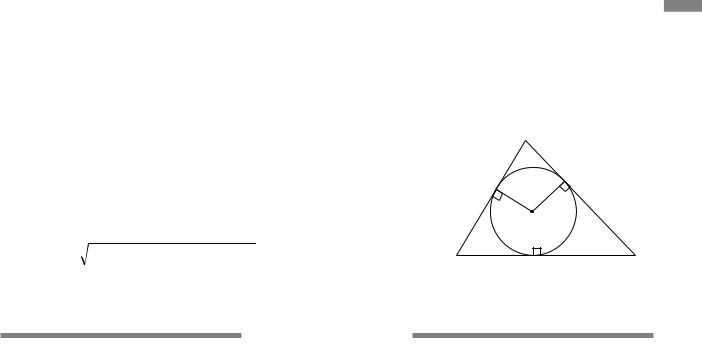
80 |
ВАРІАНТ 26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.3. |
У |
трикутнику |
ABC |
|
сторона AC дорівнює 29 см, OM, |
|
|
|
|
|
||||||||||||||||||
|
|
ON, OK — радіуси вписаного кола, CN = 24 см, BN = 1 см. |
|
|
|
|
|
|||||||||||||||||||||
|
|
BC = BN + CN = 25 см. За властивістю дотичних, проведених |
B |
|
|
|
|
|||||||||||||||||||||
|
|
до кола з однієї точки, |
CN = CK = 24 см, BM = BN = 1 |
см, |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
AM = AK = AC− KC = 29− 24 = 5 см. |
|
|
|
N |
|
|
||||||||||||||||||||
|
|
Тоді AB = AM + BM = |
5+ 1= 6 см. |
|
|
M |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
p = |
AB+ BC + AC |
= |
6 + 25+ 29 |
= 30 см. |
|
|
|
O |
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
SABC = |
|
30(30− 6)(30− 25)(30− 29) = 60 см2. |
A |
|
|
|
|
C |
||||||||||||||||||
|
|
|
|
K |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Відповідь. 60 см 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частина четверта |
|
|
|
|
|
|
|
4.1.М |
|
|
2 |
+ |
2y |
2 |
− 4xy = 17, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
y2 − x2 = 16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Помножимо перше рівняння системи на 16, друге — на –17, додамо почленно одержані |
||||||||||||||||||||||||||
|
|
рівняння, дістанемо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
65x2 + 15y2 − 64xy = 0 (*) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Оскільки (0;0) |
не є розв’язком вихідної системи, то поділимо обидві частини рівняння (*) |
|||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
x |
|
|
|
|
|
|
|||
|
|
на y |
|
, дістанемо: 65 |
|
|
|
|
− 64 |
|
|
+ 15 = 0. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
y |
|
|
|
|
|
|
|||
|
|
Нехай |
|
x |
|
|
= t, тоді рівняння набуде вигляду: 65t2 − 64t+ 15 = 0, звідки t = |
3 |
|
або t = |
5 |
. |
||||||||||||||||
|
|
|
y |
|
|
5 |
13 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
||||
Отже, система рівнянь рівносильна сукупності двох систем:
x |
= |
3 |
|
|
|
x |
= |
15 |
|
|
||||||
|
|
|
|
|
, |
|
або |
|
|
|
|
|
|
, |
||
|
|
5 |
|
|
|
13 |
|
|||||||||
y |
|
|
|
y |
|
|
|
|||||||||
|
2 |
− x |
2 |
= 16 |
|
|
2 |
− x |
2 |
= 16. |
||||||
y |
|
|
|
|
y |
|
|
|||||||||
|
|
|
|
y = |
5x |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
5x |
|
|
y = |
5x |
, |
|
x = 3, |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= 5; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Розв’яжемо першу систему: |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
, |
|
3 |
|
|
y |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
25x2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
3 |
|
|
x = 3, |
|
|
|
x |
= − |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− x |
|
|
|
|
|
= 9; |
|
|
|
|
|
|
|
|
|
|
3, |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 16; x |
|
|
|
|
|
|
|
|
|
y |
= −5. |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = −3; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13x |
|
|
x = |
|
|
|
, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
13x |
|
|
|
|
|
|
y |
= |
|
|
|
|
|
|
, |
13 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
13x |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
y = |
|
; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
y |
= |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Розв’яжемо другу систему: |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
169 |
|
|
|
|
|
|
|
|
|
|
x = |
|
|
|
, |
|
|
|
|
|
|
5 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
− x |
2 |
|
= 16; |
|
|
|
2 |
− x |
2 |
= 16; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
5 |
|
|
x = − |
|
|
|
, |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
x = − |
|
|
|
|
|
|
|
|
3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
13 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = − |
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
5 |
|
|
13 |
|
|
|
|
|
|
|
|
5 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Відповідь. (3;5), (−3;− 5), |
|
|
|
; |
|
|
|
|
|
|
, |
|
|
|
− |
|
|
;− |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ВАРІАНТ 27 81
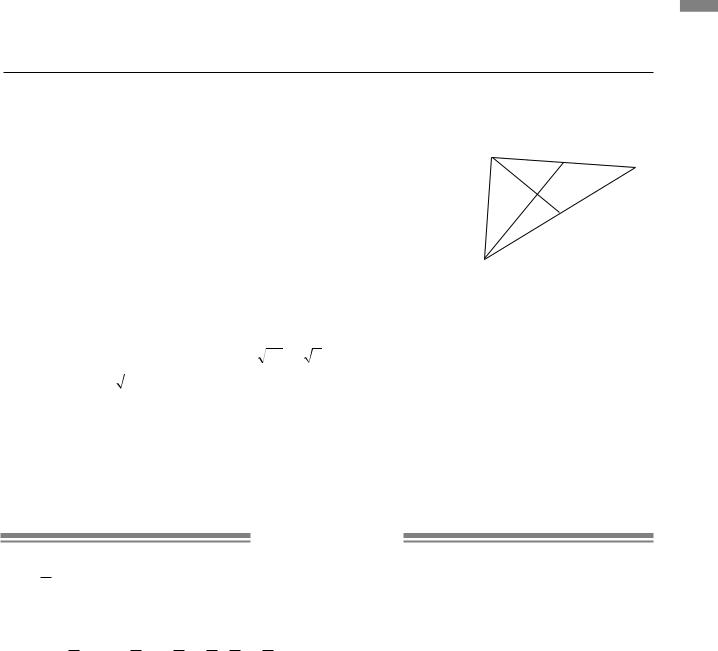
4.2.М На рисунку зображено трикутник |
ABC, у якого AC = 8 см, |
|
BC =6 см. Медіани AM1 і BM2 перпендикулярні і перетина- |
|
|
ються в точці O. Нехай AO = 2a, BO = 2b, тоді за властивістю |
|
|
медіан: OM1 = a, OM2 = b. Із трикутника AOM2 за теоремою |
B |
|
Піфагора маємо: 4a2 +b2 =16. |
|
|
Із трикутника BOM1 : 4b2 +a2 =9. |
|
|
Почленно додамо ці рівності, дістанемо: 5a2 +5b2 =25, |
|
|
a2 +b2 =5. (*) |
|
|
Помножимо рівняння (*) на 4: |
A |
|
4a2 +4b2 =20 або (2a)2 +(2b)2 =20, |
|
|
AO2 +BO2 =20. |
|
|
Оскільки трикутник ABO прямокутний, то за теоремою Піфагора: |
|
|
AB2 = AO2 +BO2 =20, отже, AB = |
20 =2 5 см. |
|
Відповідь. 2 5 см.
M1
C
 O
O
M2
Варіант 27
Частина перша
1.1.12 т + 150 кг = 500 кг + 150 кг = 650 кг.
Відповідь. Б).
1.2.9−4 52 =9−4− 52 =5− 52 =4 55 − 52 =4 53 .
Відповідь. В).
1.3.(a+3)(b−4) =ab−4a+3b−12.
Відповідь. Г).
1.4. |
Оскільки 1≠ −4 (−1) +3, 5 ≠ −4 2+3, −1= −4 1+3, 1≠ −4 1+3, то графіку функції належить |
|||||||||||
|
точка (1;−1). |
|
|
|
|
|||||||
|
Відповідь. В). |
|
|
|
|
|||||||
1.5. |
|
4x |
3 |
2 |
= |
42 |
(x3 )2 |
= |
16x |
6 |
. |
|
|
|
|
|
|
|
|||||||
5y |
52 |
y2 |
25y2 |
|||||||||
|
|
|
|
|
|
|||||||
Відповідь. Б).

82 |
ВАРІАНТ 27 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6. |
8 |
= |
8( 3 +1) |
= |
8( 3 +1) |
= |
8( |
3 +1) |
= |
8( |
3 +1) |
=4( 3 +1). |
|
|
( 3 −1)( 3 +1) |
|
|
|
|
|
|||||||
|
|
3 −1 |
|
( 3 )2 −12 |
3−1 |
|
|
2 |
|
||||
Відповідь. Г).
1.7.Відповідь. В).
1.8.Оскільки серед наведених даних значення 38 трапляється найчастіше, то мода отриманих даних дорівнює 38.
Відповідь. Г).
1.9.Відповідь. Б).
1.10. Нехай MN — середня лінія трапеції ABCD. Відрізок KN є середньою лінією трикутника BCD,
NK = 12 BC = 12 4 =2 см.
Відрізок MK є середньою лінією трикутника ABD,
MK = 12 AD = 12 10 =5 см.
Відповідь. А).
1.11.Нехай BD — висота рівнобедреного трикутника ABC. Тоді з прямокутного трикутника ADB:
AD = ABcosA =8cos30°=8 23 =4 3 см.
Оскільки висота рівнобедреного трикутника є його медіаною,
то |
AC =2AD =2 4 3 =8 3 см. Тоді площа трикутника |
||
S = |
1 |
AB AC sin A. |
|
2 |
|||
|
|
||
Враховуючи,що sin A =sin30°= 12 , S = 12 8 8 3 12 =16 3 см2.
Відповідь. Г).
BC
M N
K
A D B
A D C
1.12. Нехай точка C(x;y) — середина відрізка AB. Тоді x = |
3−1 |
=1, y = |
−2+4 |
|
=1. Відстань від точ- |
||||||||||||||||
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
ки C(1;1) |
до точки O(0;0) |
дорівнює 12 +12 = |
2 . |
|
|
|
|
|
|
|
|
|
|
||||||||
Відповідь. В). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Частина друга |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
x |
6 |
|
|
x |
|
|
6(x −2) + x(1+ x) |
= |
|
6x |
||||||||
2.1. За умовою |
|
|
+ |
|
= |
|
|
|
. ОДЗ: x ≠ −1, |
x ≠2. |
|
|
|
|
|
. |
|||||
|
1+ x |
x −2 |
1+ x |
x −2 |
(1+ x)(x −2) |
|
(1+ x)(x −2) |
||||||||||||||
6x−12+x+x2 =6x, x2 +x−12 =0, x1 = −4, x2 =3. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Відповідь. |
−4; 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ВАРІАНТ 27 83
2.2.Оскільки графік функції y = kx+ b паралельний осі абсцис, то k =0. Оскільки він проходить через точку B(3;−2), то b = −2.
Відповідь. k =0, b = −2.
2.3.0,2(3) =0,2+0,03+0,003+...= 307 , 0,(15) =0,15+0,0015+0,000015+...= 335 .
0,2(3) −0,(15) = |
7 |
− |
5 |
= |
77 −50 |
= |
27 |
= |
|
9 |
. |
|
|
|
|
|||
|
|
|
330 |
|
|
|
|
|
|
|||||||||
|
|
30 |
33 |
330 |
|
110 |
|
|
|
|
|
|||||||
Відповідь. |
9 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
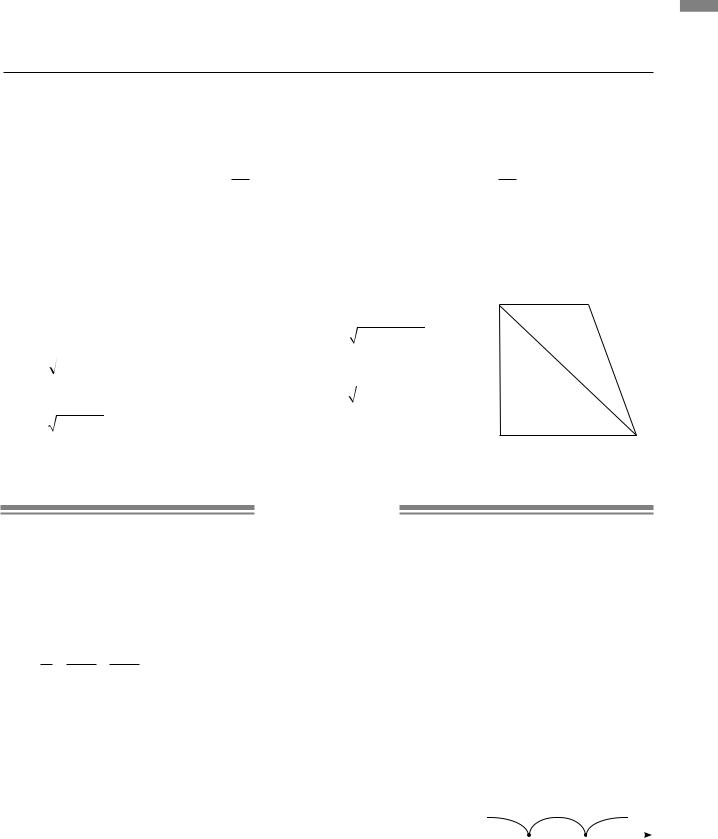
2.4. Нехай CK — висота трапеції. CK =12см, AK =4 см. |
B |
C |
|
|||||||||||||||
|
|
|
||||||||||||||||
З |
прямокутного |
трикутника |
ABD: |
AD = |
BD2 − AB2 |
= |
|
|
||||||||||
= |
152 −122 |
=9 (см). Тоді KD = AD− AK =9−4 =5 (см). |
|
|
|
|||||||||||||
З |
прямокутного |
трикутника |
CKD: |
CD = |
CK2 + KD2 |
= |
|
|
||||||||||
= 122 +52 =13 (см). |
|
|
|
|
|
|
|
|
|
A |
|
D |
||||||
Відповідь. 13 см. |
|
|
|
|
|
|
|
|
|
|
|
K |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Частина третя
3.1.Нехай слюсар може виконати замовлення за x год, тоді перший учень виконає замовлення
за (x+4) год, а другий учень — за (x+9) год. За одну годину слюсар виконає |
1 |
частину |
|||||
x |
|||||||
|
|
|
|
|
|
||
замовлення, перший учень — |
1 |
, а другий — |
1 |
частини замовлення. Враховуючи, що |
|||
x +4 |
x +9 |
||||||
|
|
|
|
|
|||
за одну годину слюсар виконує такий об’єм роботи, як два учні разом, складаємо рівняння:
x1 = x1+4 + x1+9 . ОДЗ: x ≠ −4, x ≠ −9, x ≠0
|
(x+4)(x+9) −x(x +9) −x(x +4) |
=0, x2 −36 =0, x1 = −6 — не задовольняє умову задачі, x2 =6. |
||||||||
|
x(x+4)(x +9) |
|||||||||
|
|
|
|
|
|
|
|
|
||
Отже, слюсар може виконати замовлення за 6 год. Тоді перший учень виконає замовлення |
||||||||||
за 10 год, а другий учень за 15 год. |
|
|
|
|
|
|
||||
Відповідь. 6 год, 10 год, 15 год. |
|
|
|
|
|
|
|
|||
3.2. Знаходимо |
область визначення |
даної |
функції. |
4−x2 0, |
|
|
|
|
||
(2−x)(2+x) 0. Нулі: x1 =2, |
|
|
|
|
– |
+ |
– |
|||
x2 = −2. D(y) = −2;2 . |
||||||||||
Найменшого значення y =1 |
функція |
набуває |
при x =2, |
|
|
|
|
|||
–2 |
2 |
x |
||||||||
x = −2, а найбільшого значення — y =3 приx =0. Отже, об- |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
ласть значень заданої функції 1;3 . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Відповідь. 1;3 . |
|
|
|
|
|
|
|
|
||
84 ВАРІАНТ 27
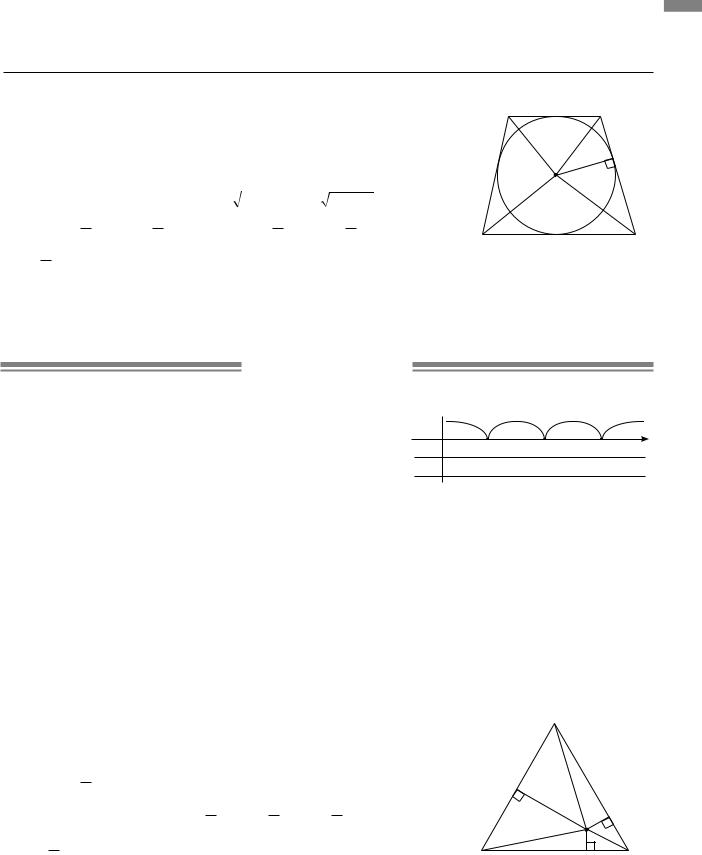
3.3.Точка O — центр кола, вписаного у рівнобічну трапе
цію ABCD, OK CD, CO = BO =6 см, DO = AO =8 см.Відомо, |
|
B |
|
|
|
|
C |
|
||||||||||||
що якщо чотирикутник описаний навколо кола, то сума кутів, |
|
|
|
|
|
|
|
|
|
|||||||||||
під якими видно з центра вписаного кола дві його протилежні |
|
|
|
|
|
|
|
K |
|
|||||||||||
сторони, дорівнює 180°. Оскільки трикутники ABO і DCO |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
рівні за трьома сторонами, то BOA = COD =180°:2 =90°. |
|
|
|
|
O |
|
|
|
|
|||||||||||
У |
трикутнику |
COD |
|
CD = |
CO2 + DO2 |
= 36+64 =10 |
см. |
|
|
|
|
|
|
|
|
|
||||
SCOD = 1 CO DO = |
1 6 8 =24; SCOD = 1 CD OK = 1 10 OK. |
|
A |
|
|
|
|
|
|
D |
||||||||||
|
2 |
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 10 OK =24, OK =4,8 см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Довжина вписаного кола l =2π OK =2π 4,8 =9,6π см. |
|
|
|
|
|
|
|
|
|
|
||||||||||
Відповідь. 9,6π см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Частина четверта |
|
|
|
|
|
|
|
|
|
|
||
4.1.М Знайдемо нулі підмодульних виразів: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x−2 =0, x =2; |
x−3 =0, x =3; |
x−4 =0, x =4. |
x – 2 |
– |
|
|
+ |
|
+ |
|
+ |
|
||||||||
Позначимо ці точки на числовій прямій і визначимо |
|
|
|
|
|
|||||||||||||||
x – 3 |
– |
2 |
|
– |
3 |
+ |
4 |
+ |
x |
|||||||||||
знаки кожного з виразів на здобутих проміжках. |
|
|||||||||||||||||||
x – 4 |
– |
|
|
– |
|
– |
|
+ |
|
|||||||||||
|
Якщо x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) |
|
(−∞;2 , то вихідна нерівність набуває |
|
|
|
|
|
|
|
|
|
|
||||||||
вигляду: −x+2−x+3 −x+4, |
−x −1, |
x 1. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
Враховуючи проміжок, на якому розв’язуємо |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нерівність, маємо: x |
|
|
(−∞;1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
Якщо x |
|
(2;3 , то нерівність набуває вигляду: x −2−x+3 |
−x+4, |
|
x 3. |
|
|
|
|
||||||||||
|
Враховуючи проміжок, на якому розв’язуємо нерівність, маємо: x =3. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
Якщо x |
|
(3;4 , то нерівність набуває вигляду: x −2+x −3 |
−x+4, |
|
3x 9, |
x 3. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Враховуючи проміжок, на якому розв’язуємо нерівність, маємо: x |
|
(3;4 . |
|
|
|
|
|||||||||||||
4) |
Якщо x (4;+∞), то нерівність набуває вигляду: x −2+x −3 x −4, |
x 1. |
|
|
|
|
||||||||||||||
|
Враховуючи проміжок, на якому розв’язуємо нерівність, маємо: x (4;+∞). |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відповідь. (−∞;1 |
3;+ ∞) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4.2.М На |
рисунку |
зображено |
|
рівносторонній |
трикутник |
ABC; |
|
|
|
|
B |
|
|
|
|
|||||
точка M — довільна точка всередині трикутника, що роз- |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
ташована на відстанях b, c і d від сторін AB, BC і AC |
|
|
|
|
|
|
|
|
|
|||||||||||
відповідно. Сполучимо точку M із вершинами трикутника. |
|
|
|
|
|
|
|
|
|
|||||||||||
SABC = 1 AC h, де h — висота трикутника ABC. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
SABC =SABM +SAMC |
+SBMC = 1 AB b+ |
1 BC c+ 1 AC d = |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
M |
c |
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
||
= 1 |
AC (b+c+d) |
(оскільки AB = AC = BC). |
|
|
A |
|
|
|
d |
|
|
C |
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Маємо: |
1 |
AC h = |
1 |
AC (b+c+d), звідки h =b+c+d, що |
|
2 |
2 |
||||
|
|
|
й треба було довести.

ВАРІАНТ 28 85
Варіант 28
Частина перша
1.1.3x =12−84, 3x = −72, x = −72:(−3), x =24.
Відповідь. В).
1.2.74 : 141 = 74 141 = 4 72 7 =8.
Відповідь. Б).
1.3.a2 −8ab+16b2 =a2 −2 4ab+(4b)2 =(a−4b)2.
Відповідь. А).
1.4.xy(2x−3y) −3y(x2 −xy) =2x2y−3xy2 −3x2y+3xy2 = −x2y.
Відповідь. Г).
1.5.Відповідь. В).
1.6. |
|
− |
3a |
5 |
2 |
= |
32 |
(a5 )2 |
= |
9a |
10 |
. |
|
|
|
|
|
|
|
||||||||
4b3 |
42 (b3 )2 |
16b6 |
|||||||||||
|
|
|
|
|
|
|
|||||||
Відповідь. Б).
1.7.Відповідь. Г).
1.8.Квадратична функція y =2x2 +12x−5 набуває найменшого значення в точці, яка є вершиною
параболи — графіка функції, тому x = − |
b |
= − |
12 |
= −3. |
2a |
|
|||
|
|
2 2 |
||
Відповідь. А). |
|
|
|
|
1.9.Оскільки при перетині двох паралельних прямих січною, утворюються або рівні кути, або такі, що їх сума дорівнює 180°. З-поміж наведених таким є кут 155°.
Відповідь. Б).
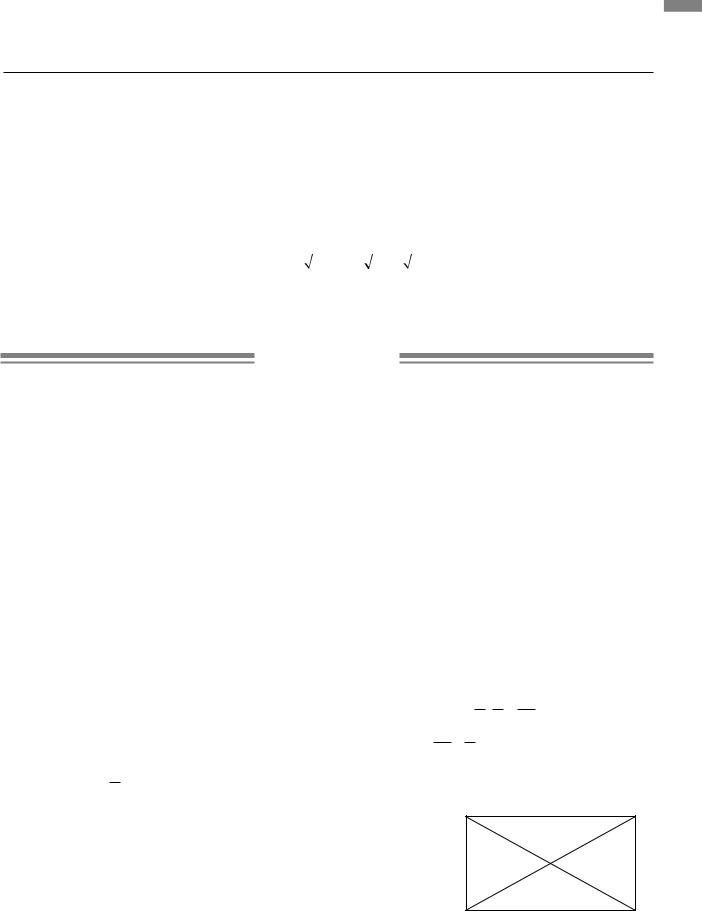
1.10. Оскільки |
AO |
= |
OC |
і AOC = BOD (як верти |
A |
|
|
|
|
|
|||||
|
OD |
|
|
|
|||
|
BO |
|
|
|
|
||
кальні), то трикутники AOC і BOD подібні за дво- |
|
O |
D |
||||
|
|
|
|
|
|
|
|
ма сторонами та кутом між ними. |
|
|
|
||||
Тому CAO = DBO =45°. |
C |
|
B |
||||
Відповідь. В).
86 ВАРІАНТ 28
1.11. Оскільки центральний кут правильного многокутника дорівнює 30°, то кут при вершині
дорівнює 150°. Тоді |
|
180(n −2) |
=150°, 180n−360 =150n, 30n =360, n =12. |
||||||||||
|
|
||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|||
Відповідь. А). |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.12. Позначимо бічну сторону рівнобедреного трикутника через |
a. |
Оскільки кут при вершині |
|||||||||||
дорівнює 30°, то площа трикутника дорівнює S = |
1 |
a2 sin30°= |
1 |
a2 |
1 |
= |
a2 |
. |
|||||
|
2 |
|
|
||||||||||
|
|
2 |
|
|
2 |
4 |
|
||||||
За умовою |
a2 |
=24, a2 =4 24, a =2 24 =2 2 6 =4 6 (см). |
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Відповідь. Г).
Частина друга
|
|
a2 |
+2a +4 |
|
a3 −8 |
|
= |
a2 |
+2a +4 |
|
|
(3a −4)(3a +4) |
= |
3a +4 |
|||||
2.1. |
|
|
|
: |
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
3a −4 |
9a2 −16 |
|
3a −4 |
(a −2)(a2 +2a +4) |
a −2 |
||||||||||||
|
Якщо a =10, то |
|
3a + 4 |
= |
3 10 + 4 |
= |
34 |
= 4,25. |
|
|
|
||||||||
|
|
a −2 |
10 −2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|||||||
Відповідь. 4,25.
2.2.За теоремою, оберненою до теореми Вієта, x1 +x2 = −p, x1 x2 =q. Тоді
Додавши почленно рівняння системи, дістанемо: 3x1 =15, q =5 (−2) = −10.
Відповідь. −10.
x1 +x2 =3,
2x1 −x2 =12.
x1 =5. Тоді x2 = −2.
2.3.Сприятливими подіями є випадки випадання на обох гральних кубиках такої кількості очок:
6 і 3, 5 і 4, 3 і 6, 6 і 3. Ймовірність кожного випадку дорівнює 16 16 = 361 . Оскільки всього таких випадків чотири, то шукана ймовірність дорівнює 4 361 = 19 .
Відповідь. 19 .
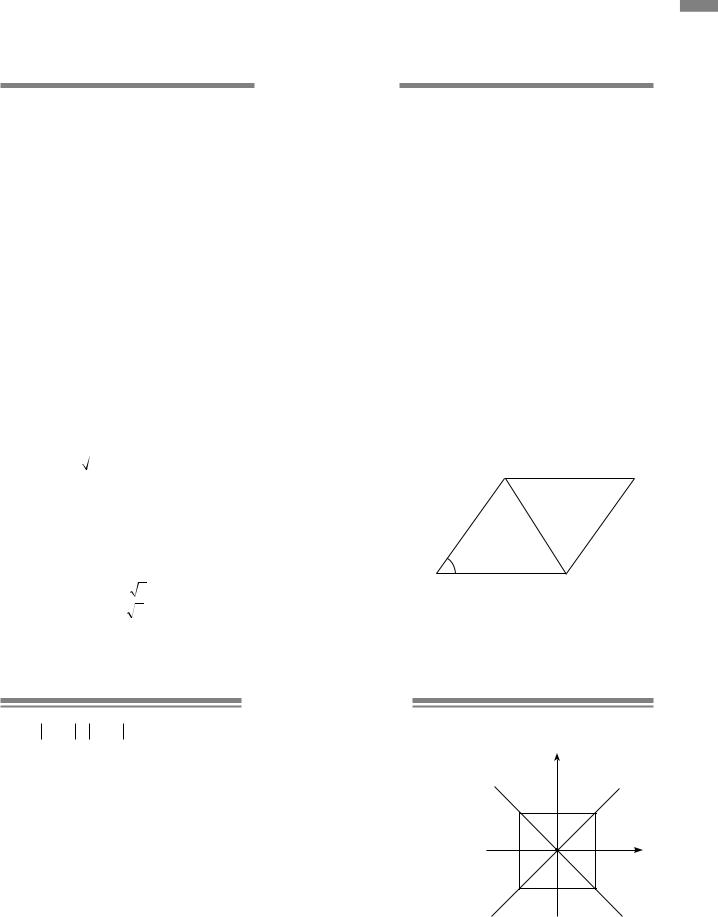
2.4. Нехай BAO = ABO = x. Тоді BOC =70+x, а суміжний із ним BOA =180−(70+x) =110−x. Тоді сума кутів трикут-
ника ABO: x+x+110−x =180, звідки x =70.
Відповідь. 70°.
B C
O
A |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВАРІАНТ 28 87 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частина третя |
|
|
|
||||
3.1. |
|
Нехай власна швидкість човна x |
км/год, а швидкість течії y км/год. Систематизуємо дані |
|||||||||||||||||
|
|
у вигляді таблиці. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рух |
|
|
|
|
|
|
|
s, км |
|
|
|
|
v, км/год |
|
t, год |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
За течією |
|
|
|
5(x+y) |
|
|
|
|
x+ y |
|
|
5 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Озером |
|
|
|
2x |
|
|
|
|
x |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проти течії |
|
|
|
2(x −y) |
|
|
|
|
x−y |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Враховуючи, що човен за течією і озером здолав 123 км, а відстань 5(x+y) у три рази більша |
||||||||||||||||||
|
|
за 2x , складаємо систему рівнянь: |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5(x+y) +2x =123, |
y =1,5. Отже, швидкість течії 1,5 км/год, власна швидкість |
||||||||||||||||
|
|
|
|
6(x−y); |
7x+5y =123, |
|||||||||||||||
|
|
|
5(x+y) = |
x =11y; |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
човна 11 1,5 = 16,5 км/год. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Відповідь. 16,5 км/год, 1,5 км/год. |
|
|
|
|
|
|
|||||||||||
3.2. |
|
(a−2)2 −5−2(a−6) >0, (a2 −6a+9)+2 >0, (a−3)2 +2 >0 |
при всіх дійсних значеннях a, 2 >0, |
|||||||||||||||||
|
|
|
отже, сума (a−3)2 +2 >0 при всіх дійсних значеннях a. |
|
|
|||||||||||||||
3.3. |
|
BD =4 3 |
|
— діагональ паралелограма |
ABCD, |
|
B |
C |
||||||||||||
|
|
|
BAD = 60°. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
ABD = 3k, CBD = k.Маємо: 60+ 3k+ k = 180, k = 30. |
|
|
|
||||||||||||||
|
|
Отже, ABD = 90°. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
У прямокутному |
трикутнику |
ABD |
|
BD |
=sin A, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AD |
A |
|
D |
|
|
|
|
AD = |
BD |
|
= |
4 3 |
=8 см. P =2( AB+ BC) =2(4+8) =24 см. |
|
|
||||||||||
|
|
|
sin A |
|
|
|
|
|||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
Відповідь. 24 см.
Частина четверта
4.1.М x−y + x+y =2.
Побудуємо на координатній площині прямі y =x і y = −x. Ці прямі розбили координатну площину на ділянки, як показано на рисунку. Точки, що розташовані на ділянці І, мають
координати (x;y) , які задовольняють умови: x > y,
x > −y.
Рівняння набуває вигляду: x−y+x+y =2, звідки x =1.
x < y,
На ділянці ІІ маємо: > −
x y.
Рівняння має вигляд: y−x+x+y =2, y =1.
y |
II |
|
|
|
|
|
1 |
|
III |
1 |
I |
O |
|
x |
|
IV |
|

88 ВАРІАНТ 29
На ділянці ІІІ маємо: x < y,
x < −y.
Рівняння має вигляд: y−x−x−y =2, x = −1.
|
|
|
|
|
|
|
|
|
|
|
|
x > y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
На ділянці ІV маємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x < −y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рівняння має вигляд: x−y−x−y =2, y = −1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Отже, шуканий графік рівняння — квадрат зі стороною 2, центром у початку координат, |
||||||||||||||||||||||||||||
діагоналі якого лежать на прямих x = y і x = −y. Шуканий графік зображено на рисунку. |
||||||||||||||||||||||||||||
4.2.М На рисунку зображено гострокутний трикутник ABC, у яко- |
|
|
B |
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
го |
AB = |
13 см, BC = |
10 |
см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Проведемо BD AC, за умовою BD = AC. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Оскільки трикутник |
ABC гострокутний, то висота BD роз- |
|
13 |
|
|
10 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ташована всередині трикутника. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Нехай AC =h, |
AD =x, тоді DC =h−x. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
За теоремою Піфагора з прямокутного трикутника |
ABD |
|
|
|
|
|
||||||||||||||||||||||
маємо: AB2 = AD2 + BD2 , 13 =h2 +x2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
За теоремою |
Піфагора з прямокутного трикутника |
BDC |
A |
|
|
|
C |
|||||||||||||||||||||
маємо: BC2 = BD2 + DC2 , 10 =h2 +(h−x)2 . |
|
|
|
|
|
|
|
D |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Дістали систему рівнянь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
+x |
2 |
=13, |
|
|
|
|
|
2 |
+10x |
2 |
=130, |
|
2 |
+x |
2 |
=13, |
|
|
|
|
|
|||||
h |
|
|
|
|
|
10h |
|
|
h |
|
|
|
|
|
|
|
||||||||||||
2h2 −2hx+x2 |
=10; |
|
−26h2 +26hx−13x2 = −130; |
16h2 −26hx+3x2 =0. |
|
|
|
|
||||||||||||||||||||
Розв’язавши однорідне рівняння 16h2 −26hx+3x2 =0 з урахуванням умови h >0, дістанемо: |
||||||||||||||||||||||||||||
|
h |
|
= |
|
3 |
,звідки x = |
2h |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Підставимо |
x = |
2h |
у рівняння h2 +x2 =13, дістанемо: h =3. Отже, AC =3 см. |
|
3 |
||||
|
|
|
Відповідь. 3 см.
Варіант 29
Частина перша
1.1.Відповідь. Г).
1.2.180 км = 18 000 000 см; 18 000 000:5000 000 =3,6 см.
Відповідь. В).
1.3.Відповідь. Б).

ВАРІАНТ 29 89
1.4. |
x3 +27 =x3 +33 =(x+3)(x2 −3x+9). |
|
Відповідь. В). |
1.5. |
6 −5 6 −3 6 = 6 (1−5−3) = −7 6 . |
|
Відповідь. А). |
1.6.Відповідь. Г).
1.7.З-поміжчиселвід1до20існуєтричисла,кратних6.Томукількістьсприятливихподійдорівнює трьом, а загальна кількість подій дорівнює 20. Отже, шукана ймовірність дорівнює 203 .
Відповідь. Г).
1.8.Відповідь. Б).
1.9.M = A = 46°. Тоді KNM =180°−(46°+54°) =80°.
Відповідь. В).
1.10. Величина прямого кута дорівнює 90°. Нехай α і β — гострі кути цього трикутника.
sinα = 23 , α =60°. Тоді β=90°−α =90°−60°=30°.
Відповідь. Г).
1.11. AB = (6−2)2 +(−3−(−1))2 = 16+4 = 20 =2 5 .
Відповідь. Б).
1.12.Площа круга S = πr2 =4π, r2 =4, r =2 (см). Сторона квадрата, описаного навколо кола, дорівнює a =2r =2 2 =4 (см).
Відповідь. В).
Частина друга
2.1.Перетворимо вираз у дужках:
|
|
x |
|
y |
|
|
|
x |
|
|
|
|
y |
|
x2 − y2 |
(x − y)(x + y) |
|
x + y |
||||||
|
|
|
|
− |
|
|
|
= |
|
|
|
− |
|
|
= |
|
= |
|
= |
|
. |
|||
|
xy − y2 |
x2 −xy |
y(x − y) |
x(x − y) |
xy(x − y) |
xy(x − y) |
xy |
|||||||||||||||||
|
Тоді |
x + y |
: |
x + y |
|
= |
x + y |
|
4xy |
=4. |
|
|
|
|
|
|
|
|||||||
|
xy |
4xy |
|
xy |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x + y |
|
|
|
|
|
|
|
|||||||||
|
Відповідь. |
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2.2. |
3−10x−5 >7x−2x−2, |
−10x−7x+2x > −2−3+5, −15x >0, |
x <0, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
6+6x+2 >3−3x+7x, |
6x+3x−7x >3−6−2, |
2x > −5, |
x > −2,5. |
||||||||||||||||||||
Розв’язком системи нерівностей є проміжок (−2,5;0). Найбільшим цілим числом із цього проміжку є число –1.
Відповідь. –1.
