Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

DPA_2011_mat-9-rozvyazannya-vsx-zavdan

.pdf

Скачиваний:

Добавлен:

15.02.2015

Размер:

2.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

70 ВАРІАНТ 23

1.11. Оскільки діагональ	квадрата є діаметром кола, описаного навколо цього квадрата, то
2R =6 2 см, R =3 2 см.
Відповідь. Б).
1.12. S = 8 10 sin150°= 80	1	= 40 (cм2).

Відповідь. А).

Частина друга

a2 −b2

(a −b)(a +b)

a +b

2.1.

−

ab −b2

b −a

b(a −b)

a −b

b(a −b)

b(a +b)

Відповідь. ab+b .

2.2.Розкладемо знаменник дробу на множники. Оскільки x2 — корені тричлена, то x2 −5x+6 =(x−2)(x−3). Тоді

x =2,001, то	1	=	1	=	1	=1000.
	x −2		2,001−2		0,001

Відповідь. 1000.

ax2 +bx+c =a(x−x1 )(x−x2 ), де x1,

x −3		x −3	1
	=		=		. Якщо
x2 −5x +6	=	(x −2)(x −3)	=	x −2	. Якщо

2.3.

Нехай робітнику, який поповнив бригаду, x років. Тоді

5 35+x

=34, 175+x =204, x =29.

Відповідь. 29 років.

2.4.

Гіпотенуза

прямокутного трикутника

AB =

. sin A =

1−cos2

A = 1−(0,8)2 =0,6 . Тоді

sin A

AB =

=10 см. AC = AB cos A =10 0,8 =8 см. P = AC+CB+ AB =8+6+10 =24 (см).

0,6

Відповідь. 24 см.

Частина третя

3.1.

Нехай власна швидкість катера x км/год. Систематизуємо дані у вигляді таблиці.

Рух

s, км

v, км/год

t, год

За течією

x+2

x +2

Проти течії

x−2

x −2

Враховуючи, що катер витратив на весь шлях 3 год, складаємо рівняння:

=3. ОДЗ: x ≠ −2, x ≠2.

x +2

x −2

40(x −2) +16(x + 2) −3(x + 2)(x −2)

=0, 3x2

−56x+36 =0, x1 =

−52

— не задовольняє умову

(x +2)(x −2)

задачі, x2 =

56 +52

=18. Отже, власна швидкість катера 18 км/год.

Відповідь. 18 км/год.

ВАРІАНТ 23 71

3.2.Нехай кількість членів арифметичної прогресії n =2. Тоді S2 =2 22 +2 =10, отже, a1 +a2 =10,

2a1 +d =10. При n =3 S3 =2 32 +3				=21, отже, 3a1 +3d =21.
Маємо систему	2a1	+d =10,	2a1	+d =10,	a1	=3,	d =7−3 =4.
		+3d =21;
	3a1		a1 +d =7.

Відповідь. 3; 4.

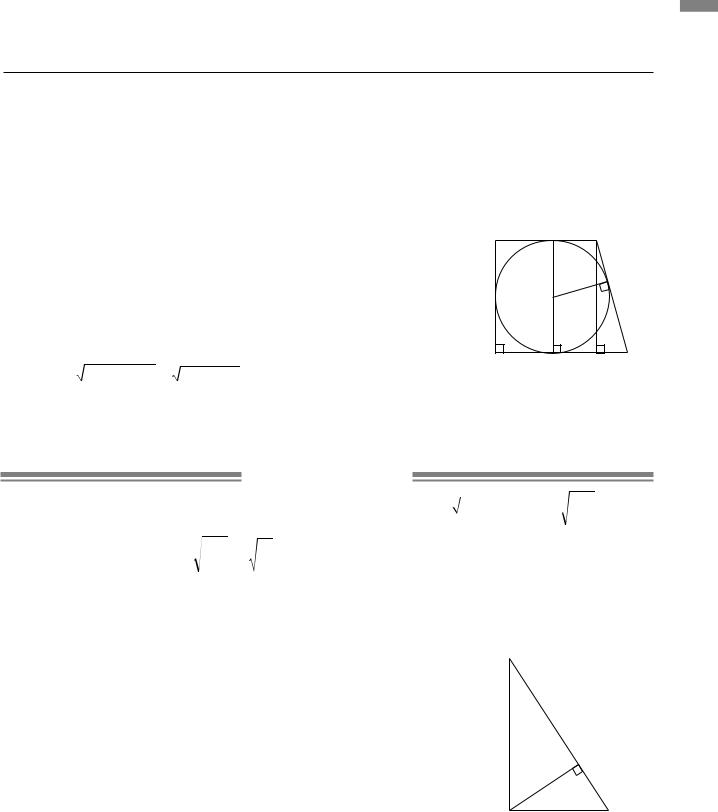
3.3.Коло з центром у точці O вписано в прямокутну тра

пецію ABCD з основами AD і BC. FN = AB, OK CD,

CK =8 см, DK =18 см. За властивістю дотичних, проведених з однієї точки до кола, CF =CK =8 см, DK = DN =18 см.

CD =CK + KD =26 см.

Проводимо CM AD.

NFCM — прямокутник. NM =CF =8 см.

DM = DN −NM =18−8 =10 см.

З прямокутного трикутника CMD маємо:

CM = CD2 −DM2 = 676−100 =24 см. AB =CM =24 см.

За властивістю сторін описаного чотирикутника

AB+CD = BC+ AD. PABCD =2( AB+CD) = 2(24+26) =100 см.

Відповідь. 100 см.

B F C

A	N	M	D

Частина четверта

4.1.М За нерівністю Коші для додатних чисел a і b маємо: a2 +b 2 a2b ;	1		1		1	.
		+ b2		2
	a				ab2

a2b

Тоді (a

+b)

, що й треба було довести.

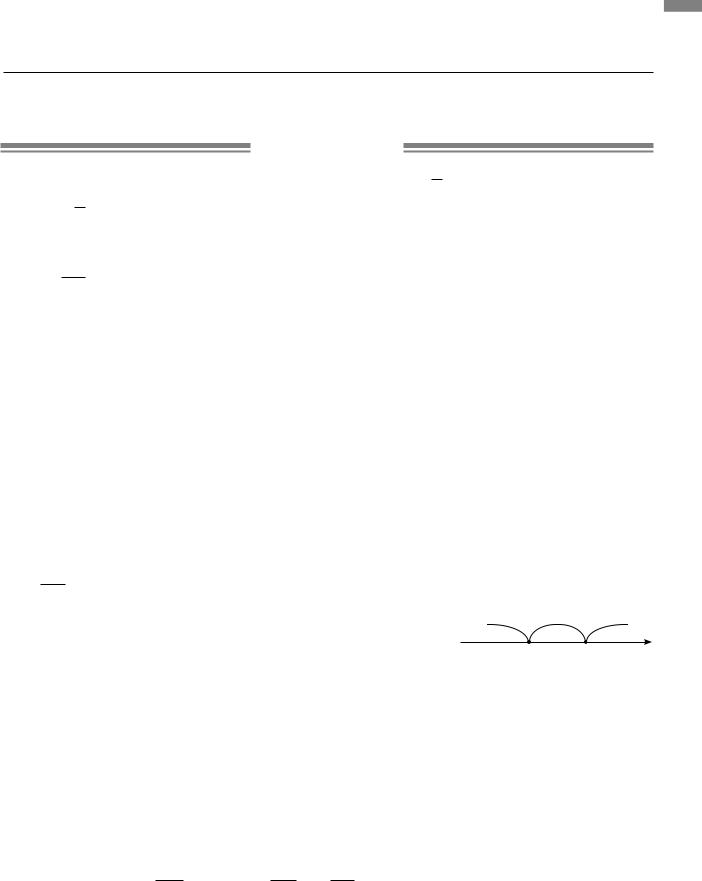
4.2.М На

рисунку

зображено прямокутний

трикутник ABC

( C =90°)

із периметром 120

см і висотою CD, що дорів

нює 24 см.

Нехай

AB =c,

AC =b,

BC =a,

CD =h,

тоді a+b+c =120,

a2 +b2 =c2, ch = ab.

Маємо систему рівнянь:

a+b+c =120,

a+b =120−c,

+2ab+b2 =1202 −240c+c2,

+b2 =c2,

=24c;

24c =ab;

−240c,

, c =50,

48c =120

288c =120

+b2 =c2,

ab =24c,

ab =1200,

=24c;

;

=2500.

Розв’язавши систему рівнянь

ab =1200,

дістанемо a =30, b =40.

a2 +b2 =2500,

Відповідь. 30 см, 40 см, 50 см.

C a B

72 ВАРІАНТ 24

Варіант 24

Частина перша

1.1.Оскільки величина розгорнутого кута дорівнює 180°, то 53 розгорнутого кута становлять

180° 53 =108°.

Відповідь. В).

1.2.x = 5108 =4.

Відповідь. Б).

1.3.Відповідь. Г).

1.4.5c2 −5d2 =5(c2 −d2 ) =5(c−d)(c+d).

Відповідь. В).

1.5. x2 =50:2, x2 =25, x1 = −5, x2 =5.

Відповідь. Б).

1.6. (−2)	−3	1	−4
			= −2−3 24 = −2−3+4 = −2.
			= −2−3 24 = −2−3+4 = −2.
		2
		2

Відповідь. Г).

1.7.25015 100%=6%.

Відповідь. Б).

1.8.ОДЗ: (−∞;+ ∞). (2x+4)(x−3) =0, якщо x1 = −2, x2 =3.

Відповідь. В).

+ – +

–2 3 x

1.9.Оскільки градусна міра зовнішнього кута дорівнює сумі двох внутрішніх кутів, не суміжних

зним, то градусна міра зовнішнього кута при вершині A дорівнює

C+ B = 100°+ 43° = 143° .

Відповідь. Б).

1.10.4:0,8 = 5.

Відповідь. Б).

1.11.Відповідь. Б).

1.12.Довжина дуги l = π180Rn . За умовою 180π6n = π, 1806n =1, n =30°.

Відповідь. А).

ВАРІАНТ 24 73

Частина друга

a +2 a −2

(a +2)2 −(a −2)2

a2 +4a +4 −(a2 −4a +4)

2.1. Перетворимо вираз у дужках:

−

a −2

a +2

(a −2)(a +2)

a2 −4

Тоді

a2 −4

при будь-яких значеннях a.

a2 −

a2 −4

Відповідь.

6x <5x−5,

x < −5,

2.2.

6x <5(x−1),

Розв’язками системи нерівностей є всі числа

>14−3x−15;

2−2x

−2x+3x > −1−7; x > −8.

з проміжку (−8;−5). З них цілими є числа −7 і −6 .

Відповідь.

−7; −6.

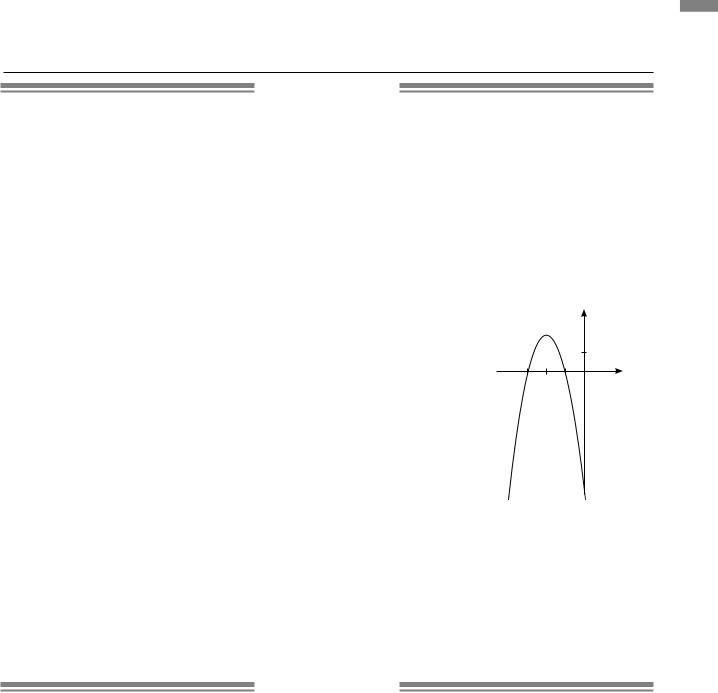
2.3.Графіком функції є парабола, вітки якої напрямлені вниз, оскільки a = −2<0. Знайдемо координати вершини параболи:

−8

−b2 +4ac

−64 +48

–3 –2

–1 0

x = −

= −2, y =

=2.

= −

2 (−2)

−8

(0;−6).

Оскільки

c = −6,

парабола проходить

через точку

Знайдемо точки перетину графіка функції з віссю абсцис:

−2x2 −8x −6 = 0, якщо x = −3 або x = −1. Отже, графік функції

перетинає вісь абсцис у точках (−3;0) і (−1;0).

–6

Користуючись рисунком,

знаходимо

проміжок зростання

(

функції: −∞;−2 .

(

Відповідь. −∞;−2 .

2.4.Нехай коефіцієнт подібності дорівнює k. Тоді 4k =20, k =5. Периметр поданого чотирикутника дорівнює P =2k+3k+3k+4k =12k см.

Тоді периметр подібного йому трикутника P1 =12 5 =60 см.

Відповідь. 60 см.

Частина третя

3.1. Нехай на склад	завезли		x кг бананів, тоді апельсинів завезли (x+100) кг. Продали
0,8(x+100) кг апельсинів			та	0,3x кг бананів, після	чого апельсинів залишилося мен-
ше на 105 кг,	ніж	бананів.		Складаємо рівняння:	(x+100) −0,8(x+100) = x−0,3x−105.
0,2x−0,7x = −105	−100	=80, x =250. Отже, на склад завезли 250 кг бананів і 250+100 =350 кг
апельсинів.

Відповідь. 350 кг, 250 кг.

3.2.22 −12 +42 −32 +62 −52 +...+1002 −992 = 3+7+11+...+199. Числа 3, 7, 11, …, 199 утворюють

арифметичну прогресію, у якої a1 =7, an =199, d =4. Знайдемо кількість членів цієї прогресії.

n = an −a1		+1 =		−3	+1=50. S50	=		+199	50 =5050.
			199	−3			3	+199
	d	4						2

Відповідь. 5050.

ВАРІАНТ 24

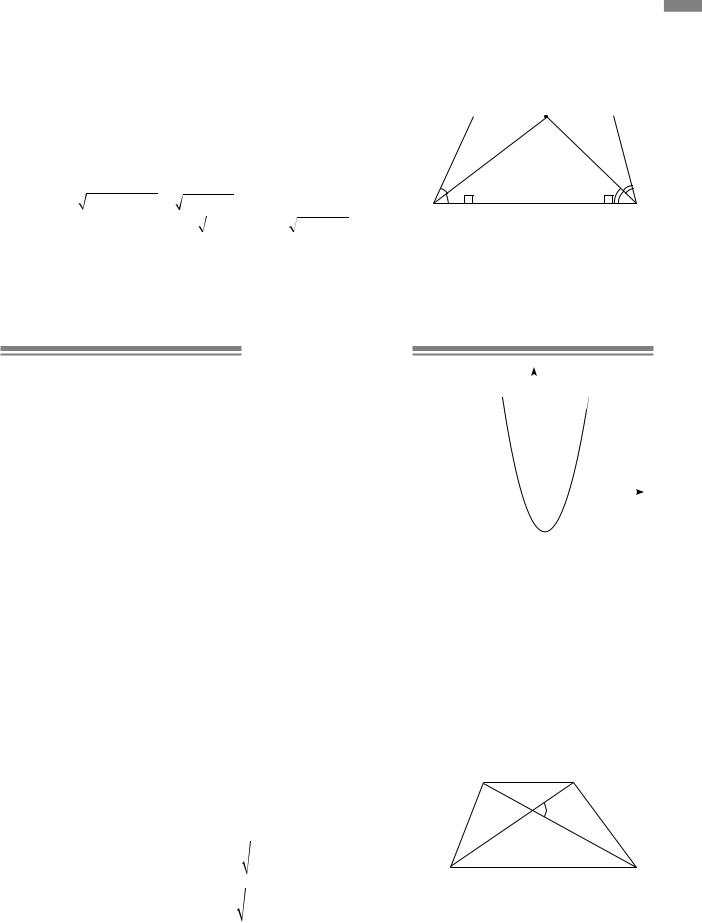
3.3.

У трапеції ABCD з основами AD і BC BAK = DAK

і ADK = CDK.

DAK = BKA

і ADK = CKD

як внутрішні

різносторонні. Отже,

трикутники ABK

і DCK рівно бедрені

. BK = AB = 10 см, CK = CD = 17 см.

DC = BK +CK =10+17 =27 см. MBCN — прямокутник,

MN = BC =27

см. З прямокутного трикутника ABM :

AM = AB2 −BM2 = 100−64 =6 см. З прямокутного A

трикутника DCN : DN = CD2 −CN2

= 289−64 =15 см.

AD = AM + MN + DN = 6+ 27+ 15 = 48 см.

SABCD =

AD + BC

BM =

48 + 27

8 =300 см2.

Відповідь. 300 см2.

Частина четверта

4.1.М Розглянемо функцію f(x) =4x2 −(3a+1)x−a−2.

Графіком цієї функції є парабола, вітки якої напрямлені вго-

ру. Рисунок, що наведено, є графічним зображенням умови

задачі.

D >0,

У системі нерівностей

f(−1) 0,

записано аналітичні

−1< x0 <2,

f(2) >0

–1

співвідношення, що описують наведений рисунок.

Оскільки в умові задачі зазначено, що рівняння має два

корені, то D >0.

Отже, складемо систему нерівностей і розв’яжемо її:

(3a+1)2 +16(a+2) >0,

9a2 +22a+33>0,

4+(3a+1) −a−2 0,

a −1,5,

3a + 1

−3

< a <5,

звідки a −1,5;1

−1<

<2,

(

)

;

16−

+1 −a−2>0;

Відповідь.

При a −1,5;1

4.2.М На рисунку зображено трапецію ABCD ( AD BC)

із діагоналями

AC і BD, що перетинаються у точці O.

За умовою SAOD =n2 , SBOC =k2 .

Нехай DOC =α, тоді

n2 = SAOD =

AO OD sinα, n =

AO OD sinα

;

k2 = SBOC =

BO OC sinα, k =

BO OC sinα .

									ВАРІАНТ 25 75

nk =	1	AO OD sinα		1	BO OC sinα =	1	AO BO sinα	1	OC OD sinα = SAOB SOCD .
nk =	2	AO OD sinα			BO OC sinα =	2	AO BO sinα	2	OC OD sinα = SAOB SOCD .
	2		2			2		2
Оскільки SABD =SACD, то SABO =SOCD .
Отже, nk = SAOB2			= SAOB . SABCD =SAOD +2SAOB +SBOC =n2 +2nk+k2 =(n+k)2 ,
що й треба було довести.

Варіант 25

Частина перша

1.1.Відповідь. Г).

1.2.(−3,5+15):(−10,8+5,8) =11,5:(−5) = −2,3.

Відповідь. В).

1.3.Відповідь. Б).

1.4.−2(x−0,5) = −3x+6, −2x+1= −3x+6, −2x+3x =6−1, x =5.

Відповідь. А).

1.5.(x+4)(x −4) = 0, x1 = −4, x2 = 4.

Відповідь. В).

3a −1

3a −(3a −1)

1.6.

−

a +1

a2 + a

a +1

a(a +1)

Відповідь. Г).

1.7. Sn	=	a1 + an	n. a8 =2,5+7 (−2)

	2

Відповідь. В).

1.8.Відповідь. Б).

1.9.Відповідь. А).

= −11,5, S8 = 2,5+(−11,5) 8 = −36.

1.10. У прямокутному трикутнику AMO ( M =90°)

AO =15 см,

MO =9 см. Катет

AM =

AO2 −MO2

= 152 −122

=9 см. Тоді

AB =2 AM =2 9=18 см.

Відповідь. Б).

1.11. Відповідь. Г).

1.12. За наслідком з теореми синусів R =

. M =180°−(80°+40°)

2sinM

Тоді R =

=2 3

см.

A O

=60°. sin60°=	3	.
	2

Відповідь. Б).

ВАРІАНТ 25

Частина друга

−1

−2

−1

1 −2

−2

2.1.

(4a4b−3 )

a−2b5

=4−1 (a4 )

(b−3 )

(a−2 )

(b5 )

a−4b3

4a4b−10

=a−4+4b3−10

=b−7 .

Відповідь. b−7 .

13 + 5 )

13 +

2.2.

13 − 5

( 13 −

5 )( 13 +

5 )

13−5

Відповідь.

13 +

2.3.2x2 −5x−18 =0, якщо x1 = −2, x2 =4,5.


Розв’язком нерівності є проміжок			−2;4,5 .
−4x+8 >0, −4x > −8, x <2, x (−∞;2) .
Тоді розв’язком системи		нерівностей		є перетин проміж

ків −2;4,5 і (−∞;2) тобто		−2;2).

Відповідь.	−2;2).

+ – +

–2 4,5 x

2.4.Точка M (x;y) — середина сторони BC. x = −42+6 =1, y = 32+1 =2. Тобто M (1;2) .

Тоді AM = (5−1)2 +(−1−2)2 = 42 +32 =5.

Відповідь. 5.

Частина третя

3.1.Нехай перший робітник може виконати завдання за x год, тоді другий робітник може викона-

ти завдання за (x−6) год. Тоді перший робітник за одну годину виконує									1	частину завдання,
									x	частину завдання,
									x
а другий —	1	частину.	1	+	1	=	1	. ОДЗ: x ≠ 0, x ≠ 6.
а другий —	x −6	частину.	x	+	x −6	=	4	. ОДЗ: x ≠ 0, x ≠ 6.
	x −6		x		x −6		4

	4(x−6) +4x−x(x−6)	=0, x2 −14x+24 =0, x1 =2 —незадовольняєумовузадачі, x2 =12.	Отже,пер-
	4x(x−6)

шийробітникможесамостійновиконатизавданняза12год,адругийробітник—за 12			−6 =6 год.

Відповідь. 12 год, 6 год.

3.2.

(

a −1)(

a −1)(a +

a +1)

a =

(

a −1)2

a =

a −1 +

a .

a + a +1

При a = 0,97	a −1	= − a +1, тоді	a −1	+ a = − a +1+ a =1.
Відповідь. 1.

ВАРІАНТ 26 77

3.3. OK BC AD,

BK =

BC =

24 =12

см, AM =

AD =

32 =16

см. BO = AO як радіуси

одного кола.

AMO : AO2 = AM2 + MO2;

Позначимо

OM =x, тоді

KO =4+x. З прямокутного трикутника

AO2 =256+x2 . З прямокутного трикутника BKO : BO2 = BK2 + KO2; BO2 =144+(4+x)2.

Дісталирівняння 144+(4+x)2 =256+x2, 8x =96, x =12.Отже, OM =12, AO = 256+144 =20 см.

Відповідь. 20 см.

Частина четверта

4.1.М

+3n2

+2n

n(n2 +3n +2)

n(n +1)(n +2)

Оскільки чисельник дробу — добуток трьох послідовних чисел, то він ділиться націло на 6

(при n =1 значення дробу дорівнює 1).

Отже, для будь-якого натурального n значення виразу

є натуральним числом.

4.2.М На рисунку зображено трикутник ABC, у якого AC =15

см,

AB+ BC =27 см; радіус вписаного кола дорівнює 4 см.

r =

SABC

, звідки SABC =rp =4 21=84 (см2).

27 – x

p( p− AB)( p−BC)( p− AC) ,

За формулою Герона: SABC =

84 = 21 6 (21−x)(x−6) , 21 6 (21−x)(x−6) =842 ,

(21−x)(x−6) =56, x2 −27x+182 =0,звідки x1 =13 або x2 =14.

Отже, маємо трикутник зі сторонами 13 см, 14 см і 15 см.

За теоремою косинусів маємо:

AB2

+ BC2

− AC2

= AB

+ BC

−2 AB

BC cosB, звідки cosB =

2 AB

cosB =

169+196 −225

140

2 13 14

13 14

Відповідь.

Варіант 26

Частина перша

1.1.789−(289−25) =789−289+25 =500+25 =525.

Відповідь. А).

1.2.Відповідь. Г).

1.3.−4x =27−11, −4x =16, x = −4.

Відповідь. В).

78 ВАРІАНТ 26

1.4.Відповідь. Б).

1.5.7x − 5y = 7yxy−5x .

Відповідь. Г).

1.6.−2x2 +3x−1=0, D =b2 −4ac =32 −4 (−2) (−1) =9−8 =1,

−b − D

−3−1

=1, x2

−b + D

−3+1

−4

Відповідь. А).

1.7.2+ 3< x+ 3< 7+ 3, 5< x+ 3< 10.

Відповідь. В).

1.8.an =a1 +(n−1)d. 29=5+(n−1) 3, n =9.

Відповідь. Б).

1.9.AOM = COM + AOC. COM = 12 COB =60°:2 =30°,

AOC = AOB− COB=180°−60°=120°. Отже, AOM =120°+30°=150°.

Відповідь. В).

1.10. Відповідь. Г).

1.11. sin120°=sin(180°−60°) =sin60°=							3	.
1.11. sin120°=sin(180°−60°) =sin60°=							2	.
							2
	Відповідь. В).
			=	2	2	=
1.12.		MN	=	(2−4) +	(−2+1) = 4+1	=	5 .
	Відповідь. А).
							Частина друга
				2					2			2		(3 2 )	2	2
2.1.	(3 2 +2 3 ) −(3 2 +2 3 )(3 2 −2 3 ) = (3 2 )								+2	3 2	2	3 +(2 3 )	−	(3 2 )	−(2	3 )	=

	=18+12			6 +12−18+12 =24+12 6 .
	Відповідь. 24+12				6 .

2.2.Рівняння параболи може бути записане у вигляді y =a(x+m) +n, де (m;n) — координати її вершини. Оскільки вершина параболи розташована в точці (0;2) , то її рівняння має вигляд:

y =ax2 +2. Коефіцієнт a знайдемо, скориставшись тим, що парабола проходить через точку B(1;6). 6 =a 12 +2, a =4. Отже, подану функцію задає формула y =4x2 +2.

Відповідь. y =4x2 +2.

					ВАРІАНТ 26 79

2.3. Пряма x−y+2 =0		і коло x2 +y2 =4 перетинаються в точках, координати яких є розв’язками
	системи рівнянь:	x−y+2 =0,		Виразимо з першого рівняння y через x	і підставимо цей вираз
			=4.
		x2 +y2

у друге рівняння системи: y =x+2, x2 +(x+2)2 =4, x2 +x2 +4x+4 =4, 2x2 +4x =0, 2x(x+2) =0, x1 =0, x2 = −2. Тоді y1 =0+2 =2, y2 = −2+2 =0.

Відповідь. (0;2) , (−2;0) .

2.4.Нехай a і b — сторони прямокутника, d — його діагональ, d =13 см, a1 =4 см і b1 =9 см — проекції сторін прямокутника на діагональ. a2 =da1 =13 4, a =2 13 , b2 =db1 =13 9, b =3 13 .

Тоді площа прямокутника дорівнює S =ab =2 13 3 13 =78 см2.

Відповідь. 78 см2.

Частина третя

3.1.Нехай швидкість руху плота x км/год. Систематизуємо дані у вигляді таблиці.

Рух

s, км

v, км/год

t, год

Пліт

Човен

18+x

18 + x

Враховуючи, що човен відчалив на 9 год пізніше, ніж пліт, складаємо рівняння:

−

=9. ОДЗ: x ≠0, x ≠ −18.

18 + x

20(18 + x) −20x −9x(18 + x)

=0, x2 +18x−40 =0, x1 = −20 — не задовольняє умову задачі, x2 =2.

x(18 + x)

Отже, швидкість руху плота 2 км/год. Тоді пліт рухався протягом 202 =10 год, човен наздогнав

пліт о дев’ятнадцятій годині. Відповідь. О дев’ятнадцятій годині.

3.2.Розв’яжемо першу нерівність системи x2 +x −6 0 методом

інтервалів. Нулі функції y =x2 +x−6

x1 = −3, x2 =2.

–

(−∞;−3

2;+ ∞) .

–3

Розв’язавши другу нерівність системи, дістанемо

x2 −x −x2 −2x −1 8, x −3.

Отже, розв’язками нерівності є x = −3

та x [2;+ ∞).

–3

Відповідь.

{−3} [2;+ ∞).

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015227.84 Кб2Doc1.doc
#
14.02.2015224.77 Кб2Doc2.doc
#
04.09.2019706.05 Кб1Dodatok_1.doc
#
15.02.201540.84 Кб4Dokument_Microsoft_Office_Word.docx
#
12.03.201615.72 Mб91dopatka_r_perepechko_a_kniga_o_sudah.pdf
#
15.02.20152.63 Mб44DPA_2011_mat-9-rozvyazannya-vsx-zavdan.pdf
#
06.11.2018148.48 Кб1dvp_pr_001.doc
#
14.02.2015318.98 Кб8Ekonomichna_istoriya_Ukrayini.doc
#
15.02.201556.71 Кб28ekonomika.docx
#
15.02.20151.71 Mб292Ekon_Pidp_ta_mij-komp-Fedorova.pdf
#
15.02.20151.04 Mб148Ekon_prom_pidpr_Maslak_2011.pdf