Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

DPA_2011_mat-9-rozvyazannya-vsx-zavdan

.pdf

Скачиваний:

Добавлен:

15.02.2015

Размер:

2.63 Mб

Скачать

☆

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

10 ВАРІАНТ 3

2.2.Нехай x1 і x2 — корені рівняння. x1 =1,5. За теоремою, оберненою до теореми Вієта, x1 x2 = −6,

x2 = −6:1,5 = −4, p = −(x1 +x2 ) = −(1,5−4) =2,5.

Відповідь. p =2,5, x2 = −4.

2.3.У сплаві 100 % – 60 % = 40 % олова, що становить 200 г. Тоді маса сплаву 200:0,4 =500 г.

Відповідь. 500 г.

			AC			2				3	2		4
2.4.	AB	— гіпотенуза трикутника ABC, AB =		. cosA =	1−sin		A =	1	−			=		.
2.4.	AB	— гіпотенуза трикутника ABC, AB =		. cosA =	1−sin		A =	1	−			=		.
			cos A							5			5

AB = 84 =10 (см).

Відповідь. 10 см.

Частина третя

3.1.Нехай власна швидкість моторного човна x км/год. Систематизуємо дані у вигляді таблиці.

Рух

s, км

v, км/год

t, год

За течією

x+3

Проти течії

x−3

Враховуючи, що шлях туди і назад човен долає за 8 год, складаємо рівняння:

=8. ОДЗ: x ≠ −3, x ≠3.

x+3

x−3

45(x−3) +45(x+3) −8(x+3)(x−3)

=0,

4x2 −45x−36 =0,

x1 =

−51

= −

не

задовольняє

(x+3)(x−3)

умову задачі, x2 =

45+51

=12. Отже, власна швидкість човна 12 км/год.

Відповідь. 12 км/год.

3.2. Область допустимих значень функції — множина розв’язків системи

x−1 0,

−4x

>0.

(1)

5x+9

x 1,

(2)

4x2 −5x−9<0.

Розв’яжемо другу нерівність системи методом інтервалів.

–

y =4x2 −5x−9; нулі: 4x2 −5x−9=0, x = −1, x =2

; x 1;2

–1

2 4

Ураховуючи нерівність (1), маємо: 1; 2

Відповідь.

1; 2

ВАРІАНТ 3 11

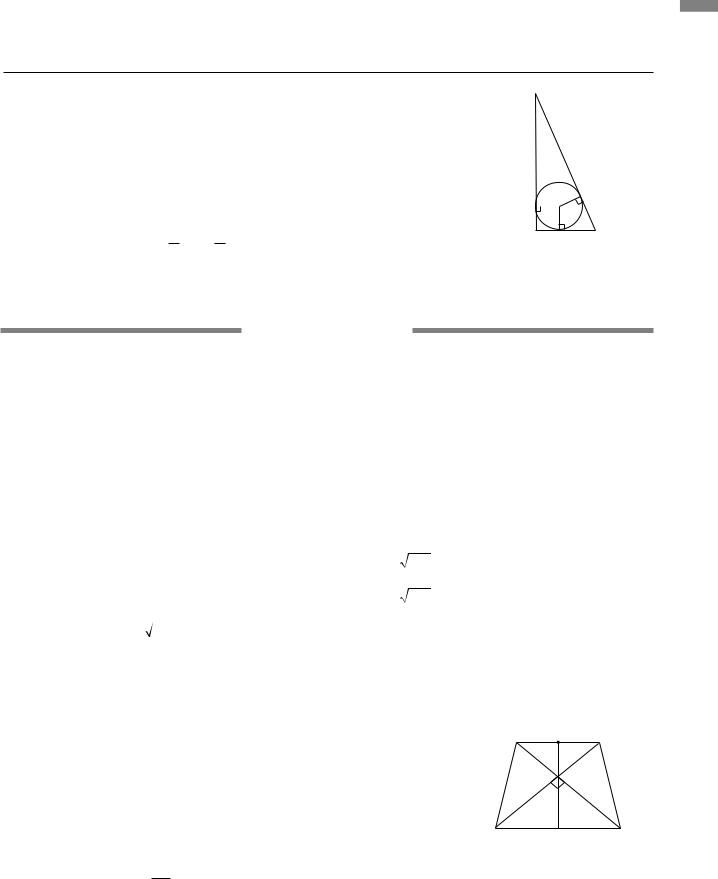
3.3.У прямокутному трикутнику ABC CD =2 см, AD =3 см, тоді

AC = CD+ AD = 2+ 3 = 5 см. OD = OE = OM = r, CEOD — ква-

драт. За властивістю дотичних, проведених з однієї точки до кола, маємо: AM = AD =3 см, CE =CD =2 см, BM = BE. Нехай BM = x,тоді BC = 2+ x, AB = 3+ x.ЗатеоремоюПіфагора

AB2 = AC2 +BC2, (3+x)2 =25+(2+x)2 , 25+4+4x+x2 =9+6x+x2 , 2x =20, x =10. Отже, BM =10 см, AB =10+3 =13 см. Радіус

описаного кола R = 12 AB = 12 13 =6,5 см.

Відповідь. 6,5 см.

O M E

C D A

						Частина четверта
4.1.М (x+2)(x+3)(x+8)(x+12) =4x2 ;					(x2 +14x+24)(x2 +11x+24) =4x2 .
Оскільки x = 0				не є коренем цього рівняння, то, поділивши його обидві частини на x,
дістанемо рівняння, рівносильне заданому.
		24			24
Маємо: x+				+14 x+		+11 = 4.

			x		x

Нехай x+	24		+11=t, тоді рівняння набуває вигляду: (t+3)t =4; t2 +3t−4 =0.
	x

Звідки t =1 або t = −4.

x = −4,

x = −6,

Далі:

x +11=1,

x2 +10x+24 =0,

x =

−15

−

129

+15x+24

=0;

+11= −4;

−15

129

x =

−15±

Відповідь.

129

; – 6; – 4.

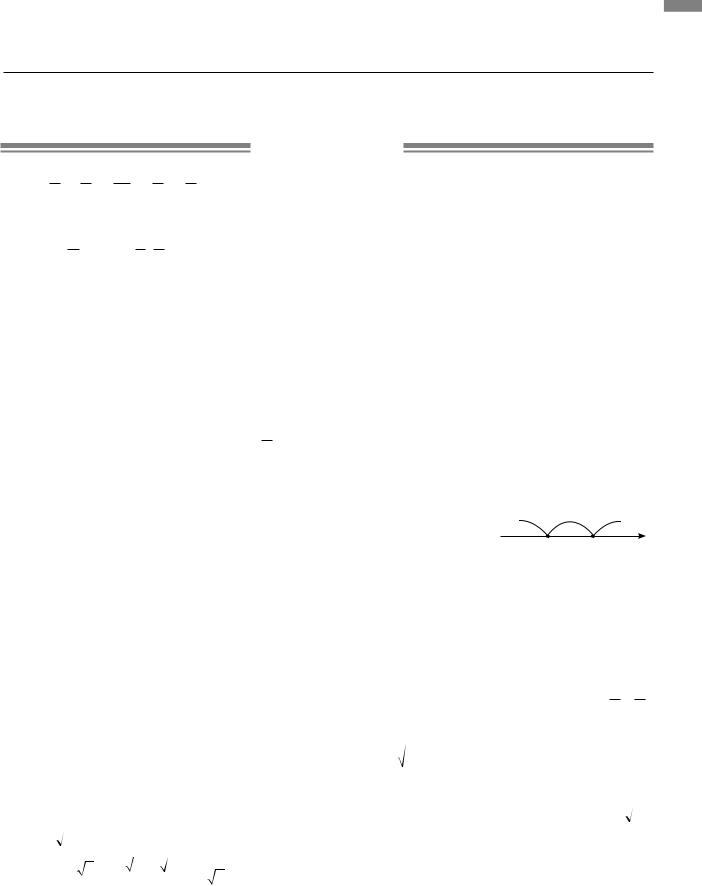
4.2.М На рисунку зображено рівнобічну трапецію ABCD ( AD BC), діагоналі якої взаємно перпендикулярні. Через точку перети-

ну діагоналей проведемо висоту трапеції,		PM = h.
Площа трапеції ABCD: S =	AD+ BC	PM.
	2

Оскільки трапеція ABCD рівнобічна і BD AC, то трикутники AOD і BOC рівнобедрені і прямокутні.

Отже, OM = AM і OP = BP, тоді

AD+BC =2 OM+2 OP =2(OM+OP) =2 PM =2h.

Маємо: S = 22h h =h2 .

Відповідь. h2.

B P C

A M D

12 ВАРІАНТ 4

Варіант 4

Частина перша

1.1.2 78 +3 58 =5 128 =6 48 =6 12 .

Відповідь. В).

1.2.0,2: 54 100%= 15 54 100%=16%.

Відповідь. Б).

1.3.Відповідь. Г).

1.4.(3x−2)2 +12x =(3x)2 −2 3x 2+22 +12x = 9x2 −12x+4+12x =9x2 +4.

Відповідь. А).

1.5.Відповідь. Б).

−2

1.6. 30 +3−4 (3−2 )−3 −(0,5)−2 =1+3−4 36 − 1 =1+32 −22 =1+9−4 =6.

Відповідь. В).

1.7.Відповідь. В).

1.8.Запишемо нерівність у вигляді x2 −49 0. ОДЗ нерівності (−∞;+ ∞).

x	2	−49	=0, якщо	x1 = −7, x2 =7. Отже, x		−7; 7
							.

Відповідь. Г).

+ – +

–7 7 x

1.9.Оскільки кути при основі рівнобедреного трикутника рівні, а сума кутів трикутника дорівнює 180°, то кут при вершині дорівнює 180°−2 30°=120°.

Відповідь. Б).

1.10.Оскільки тангенс гострого кута прямокутного трикутника — це відношення протилежного

катета до прилеглого, то тангенс кута, протилежного до більшого з катетів, дорівнює 68 = 43 .

Відповідь. В).

1.11. Нехай точка O(0;0) — початок координат. Тоді AO =							(−8−0)2 +(6−0)2 =10.
Відповідь. Г).
1.12. Сторона			рівностороннього трикутника, вписаного в				коло радіуса R , дорівнює	a = R 3 =
=4 3		см. Площу			рівностороннього трикутника зі		стороною a обчислимо за	формулою
S =	a2	3	=	(4 3 )2	3	=12 3 (см2).
		4		4

Відповідь. Б).

ВАРІАНТ 4 13

Частина друга

2.1.

Перетворимо вираз у дужках:

+5b

−

−5b

a+5b

−

a−5b

(a+5b)2 −(a−5b)2

+5ab

a(a−5b)

a(a+5b)

a(a−5b)(a+5b)

−5ab a

20ab

a+5b

−

a−5b

25b2 −a2

20ab

25b2

−a2

= −

. Отже,

a(a

−

25b

)

−5ab

a(a

−25b

)

+5ab

Відповідь. −

2.2.

18−3(1−x)

2x−7+2(7x−2)

18−3+3x 2x−7+14x−4, −13x −26, x 2. Розв’язками нерів

ності є всі числа з проміжку (−∞; 2 , із них натуральними є числа 1 і 2.

Відповідь. 1; 2.

2.3.

Графіком

функції

є парабола, вітки якої

напрямлені

вниз,

оскільки

a = −2<0.

Знайдемо

координати

вершини

параболи:

x = −

= −

=1,

y = −2 1+4 1=2. Оскільки

c =0, парабола про-

2 (−2)

ходить через точку (0;0). Знайдемо точки перетину графіка функції

з віссю абсцис: −2x2 +4x = 0,

−2x(x −2) = 0,

x = 0

або

x =2. Отже,

графік функції перетинає вісь абсцис у точках (0;0) і (2;0).

Користуючись

рисунком,

знаходимо

область

значень цієї

функції: (−∞;2 .

(

Відповідь. −∞;2 .

2.4.Нехай кут між векторами дорівнює α. З означення скалярного добутку векторів випливає, що

cosα =

m n = −3

(−2) +0

2 =6,

(−3) +

=3,

(−2) +2

=2 2 .

Тоді cosα =

, α =45°.

2 2

Відповідь. 45°.

Частина третя

3.1.

Нехай

2n−1,

2n+1,

2n+3,

2n+5

—

послідовні

непарні

натуральні числа.

Тоді

(2n+1)(2n+3) −111=3((2n−1) +(2n+5)), 4n2 −4n−120 =0, n1 =6, n2 = −5 — не є натуральним

числом. При n =6

2n−1=2 6−1=11, 2n+1=2 6+1=13, 2n+3 =2 6+3 =15, 2n+5 =2 6+5 =17.

Відповідь. 11; 13; 15; 17.

y =6−x,

(1)

3.2.

=2,5. (2)

6−x

=2,5. Нехай

=t,

Підставимо (1) в (2) і розв’яжемо отримане рівняння:

−x

тоді t+

=2,5, t2 −2,5t+1=0, t1

, t2

=2. Отже,

, x =2 або

=2, x =4.

−x

При x =2

y =6−2 =4; при x =4 y =6−4 =2.

Відповідь. (2;4), (4;2).

14	ВАРІАНТ 5

3.3.	Знаходимо діагоналі чотирикутника ABCD. BD =						(xB −xD )2 +(yB −yD )2 =													(−1−2)2 +(−2−3)2 =
	= 9+25 = 34 ; AC = (xC −xA )2 +(yC −yA )2 = (−2−3)2 +(−1−2)2 = 9+25 = 34 .
	Координати середини діагоналі AC:		x =			xA +xC			=		3−2	=		1	,	y =			yA +yC		=		−1+2	=	1	. Коор-
											2			2					2			2
			2																					2
	динати середини діагоналі BD: x =	xB +xD		=	2−1		=	1		,	y =		yB +yD					=	3−2	=	1	. Таким чином,
								2											2		2
	2		2											2
	діагоналі чотирикутника ABCD рівні, перетинаються в точці													1		;	1		та цією точкою діляться


														2			2

навпіл. Отже, чотирикутник ABCD є прямокутником.

Частина четверта

4.1.М Нехай подія A — витягли три кульки, серед яких дві білі й одна чорна. Кількість рівномож

ливих результатів дорівнює C3 .

Вибрати дві білі кульки можна C2 способами, одну чорну — C1

способами.

C2 .

Отже, кількість результатів, що сприяють події A, дорівнює C1

P( A) =

C181 C122

18! 12! 3! 27!

594

≈0,2292 .

17! 2! 10! 30!

2030

Відповідь. ≈0,2292 .

4.2.М На рисунку зображено трикутник ABC, CM — медіана,

CM =m, ACM = α, BCM =β.

«Подвоїмо»

медіану

CM,

дістанемо паралело-

грам

AKBC, кути

якого

дорівнюють: BCA =α+β,

CAK =180°−(α+β) .

З трикутника AKC за теоремою синусів:

sinKCA

sinCAK

sinCKA

Звідки AK =

2msinα

AC =

2msinβ

sin(α+β)

Оскільки AKBC — паралелограм, то AK = BC, отже, BC =

2msinα

sin(α+β)

Відповідь.

AC =

2msinβ

BC =

2msinα

sin(α+β)

Варіант 5

Частина перша

1.1.Відповідь. Б).

1.2.(−7,5−3) (−1,2+1,5) = −10,5 0,3 = −3,15.

Відповідь. Г).

ВАРІАНТ 5 15

1.3.Оскільки −2+(−3) = −5 ≠5, −2+3 =1≠5, 2+3 =5, −3+2 = −1≠5, то розв’язком рівняння є пара чисел (2;3).

Відповідь. В).

1.4.2x−0,5 =2,5−1,5x, 2x+1,5x =2,5+0,5, 3,5x =3, x =3:3,5 =3: 72 =3 72 = 76 .

Відповідь. Б).

1.5.За теоремою Вієта x1 +x2 = −8, x1 x2 =7. Ці умови задовольняють числа −7 і −1.

Відповідь. А).

2a+b

2a+b+1 (a−b)

1.6.

a2 −b2

a+b

(a−b)(a+b)

a+b

(a−b)(a+b)

a2 −b2

Відповідь. Г).

1.7.

d =a2 −a1 . Оскільки a2 =3, a1 =8, то d =3−8 = −5.

Відповідь. Б).

1.8.

5+x 2,

x −3,

x−6<2x

x > −6.

Розв’язком системи нерівностей є проміжок (	−6; −3	–6	–3	x

	.

Відповідь. В).

1.9.Радіус кола дорівнює 8:2 =4 см. Оскільки пряма віддалена від центра кола на відстань, що дорівнює його радіусу, то пряма має з колом одну спільну точку.

Відповідь. А).

1.10.Оскільки прямокутний трикутник рівнобедрений, то його катети рівні. Нехай катети дорів нюють x см. Тоді за теоремою Піфагора x2 +x2 =(4 2 )2 , 2x2 =32, x2 =16, x =4.

Відповідь. Б).

1.11.		AB(−1−(−3); −2−2), AB(2;−4).
	Відповідь. В).
1.12. За теоремою косинусів													AC2 = AB2 +BC2 −2 AB BC cosB.
				Враховуючи, що cos120°= −															1	, AC2 =52 +32 +2 5 3								1	= 49,		AC =7.
				Враховуючи, що cos120°= −															2	, AC2 =52 +32 +2 5 3								2	= 49,		AC =7.
	Відповідь. Г).																		2									2
	Відповідь. Г).
																					Частина друга
			−3				−2	5		−3		5	−2			4 3					2 2		64		4		64+20			84
2.1.	1,25			+2,5				=				+			=		+					=		+		=			=		.
2.1.	1,25			+2,5				=				+			=		+					=	125	+	25	=	125		=	125	.
								4				2				5					5		125		25		125			125
	Відповідь.							84	.
	Відповідь.						125		.
							125
		a+5		a				a (		a		+5)		=		a
2.2.					=													.
2.2.		a−25			=	(		a −5)(				a +5)			a −5			.
	Відповідь.							a			.
	Відповідь.										.
								a −5

16 ВАРІАНТ 5

2.3.Функція y = −2x2 +5x−2 визначена при всіх дійсних x. Знай-

демо нулі функції: −2x2 +5x−2 =0, якщо x1 =0,5,		x2 =2. Роз	–	+	–
			0,5	2		x
в’язком	нерівності є всі числа з проміжку	. З них
	0,5; 2

цілими є числа 1 і 2.

Відповідь. 1; 2.

2.4.Оскільки точка розташована на осі абсцис, то її ордината дорівнює нулю.

Нехай точка C(x;0) рівновіддалена від точок A і B. CA2 =(x−1)2 +(0−5)2 =(x−1)2 +25;

CB2 =(x−3)2 +(0−1)2 =(x−3)2 +1. CA =CB, тому (x−1)2 +25 =(x−3)2 +1.

Розв’язавши це рівняння, дістанемо x = −4.

Відповідь. (−4;0).

Частина третя

3.1. Нехай знаменник дробу —

x, тоді

чисельник — x−5, дріб

можна записати

у вигляді

x−5

. Після додавання до чисельника 3, а до знаменника — 4, дістанемо дріб

x−2

, який

x+4

x−5

x−2

більший від заданого дробу

на

Маємо рівняння

. ОДЗ: x ≠ −4,

x ≠0.

8(x−5)(x+4) +x(x+4) −8x(x−2)

x+4

=0, x2

+12x−160 =0, x1 = −20, x2 =8.

8x(x+4)

При x1 = −20 дістанемо скоротний дріб 2025 , що не задовольняє умову.

При x2 =8 дістанемо дріб 38 , що задовольняє умову.

Відповідь. 38 .

3.2. 9a2 +a2 −6a−2ab+b2 +2 >0, (9a2 −6a+1)+(a2 −2ab+b2 )+1>0, (3a−1)2 +(a−b)2 +1>0. Оскільки

(3a−1)2 0 при будь-яких значеннях a, (a−b)2 0 при будь-яких a і b, 1>0, то сума (3a−1)2 +(a−b)2 +1>0 для всіх дійсних значень a і b.

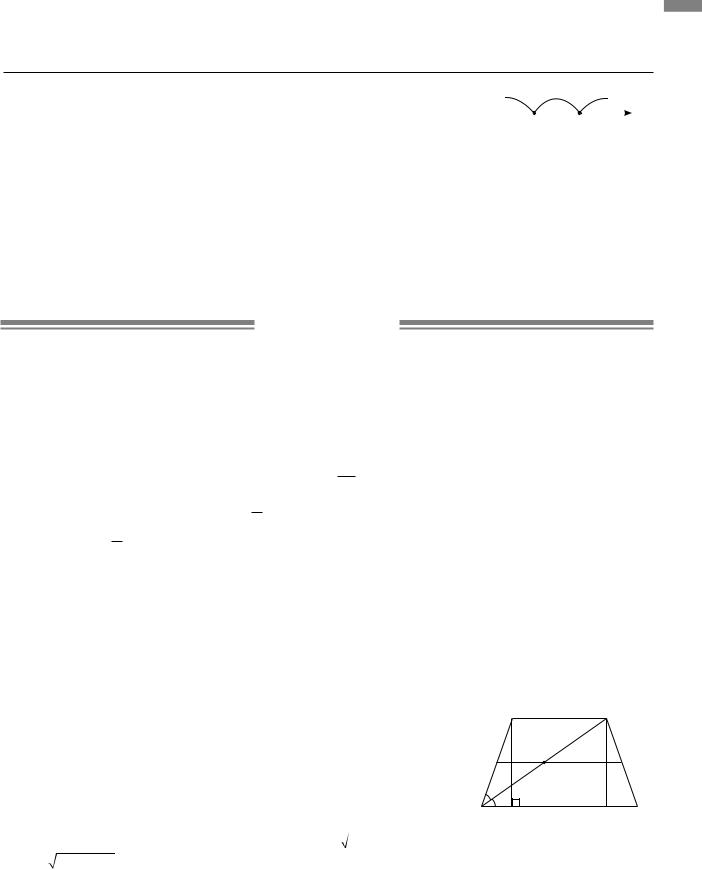
3.3.Діагональ AC рівнобічної трапеції ABCD ділить середню лінію MN на відрізки MO =13 см, NO =23 см. За властивістю середньої лінії трикутника BC =2MO =2 13 =26 см, AD =2N0 =

=2 23=48 см. BAC = DAC( AC —бісектриса), DAC = BCA

як внутрішні різносторонні при паралельних прямих AD і BC та січній AC. Отже, трикутник ABC рівнобедрений, у нього

AB = BC =26 см.

Проводимо BE AD і CF AD. BCFE — прямокутник,

EF = BC =26 см. AE = FD =(AD−EF):2 =(46−26):2 =10 см.

З прямокутного трикутника ABE BE =					AB2 − AE2 =
= 676−100 =24 см.
Площа трапеції S =	AD+ BC	BE =	46+	26	24 =864 см2.
Площа трапеції S =	2	BE =	2		24 =864 см2.
	2		2

Відповідь. 864 см2.

	M	O		N
		O
A	E		F	D
	E		F

			ВАРІАНТ 6								17

		Частина четверта
			m+1			1				3
4.1.М Система рівнянь	(m+1)x+y =3,	не має розв’язків за виконання умов:	m+1	=		1			≠	3	.

			2			(m		2)		6
	2x−(m−2)y =6		2		−	(m	−	2)		6
					−		−

Розв’яжемо рівняння

m+1

; 2m−m2 +2−m =2, m2 −m =0, звідки m =0 або m =1.

−m

m+1

≠

Перевіримо, чи задовольняють здобуті значення m умову

m+1

Якщо m =0, то

, що не задовольняє зазначену умову.

Якщо m =1, то

m+1

=1≠

, що задовольняє умову.

Відповідь. m =1.

16a2

+24a

= 16

2 +24

cos120°+9

4.2.М

+3b

= (4a+3b)

= 16 9−12 3 2+9 4 =

108 =6 3 .

Відповідь. 6

3 .

Варіант 6

Частина перша

1.1.432 48−38 432 =432(48−38) =432 10 =4320.

Відповідь. Г).

1.2.Відповідь. В).

1.3.Відповідь. Б).

1.4.Відповідь. А).

1.5.	3a	+	5b	=	3a a+5b b	=	3a2 +5b2	.
	b		a		ab
							ab

Відповідь. Г).

1.6.Оскільки дискримінант D =b2 −4ac =(−5)5 −4 3 2 =1>0, то рівняння має два корені.

Відповідь. А).

1.7.1 5<5a <3 5, 5<5a <15.

Відповідь. В).

1.8.an =a1 +(n−1)d. a5 =a1 +4d, a1 =a5 −4d =35−4 6 =35−24 =11.

Відповідь. Б).

18 ВАРІАНТ 6

1.9.Нехай коефіцієнт пропорціональності дорівнює k. Тоді 5k+2k =70, звідки k =10. Отже, точка лежить від кінців відрізка на відстані 50 см і 20 см.

Відповідь. В).

1.10.Оскільки діагоналі ромба є бісектрисами його кутів, то ABC =2 75°=150°.

Відповідь. Г).

1.11. За теоремою синусів											MN	=	MK		,	звідки MN =	MK sinK	. Враховуючи, що		sin45°=					2		,
1.11. За теоремою синусів												=	sinN		,	звідки MN =		. Враховуючи, що		sin45°=				2			,
											sinK		sinN				sinN							2
													6	2
sin60°=						3		, дістанемо MN =					6	2		=2 6 .
						3								2
					2									3
					2									3

														2
Відповідь. Б).
1.12. Вектори колінеарні,										якщо їх відповідні координати пропорційні. Оскільки									2	=	3	,	2	≠		3		,
1.12. Вектори колінеарні,										якщо їх відповідні координати пропорційні. Оскільки									6	=	9	,	3	≠	4			,
																			6		9		3		4
	2	≠	3	,	2		≠	3	, то вектору a(2;3)					колінеарний вектор, що має координати (6;9) .
1		≠		,	9		≠	6	, то вектору a(2;3)					колінеарний вектор, що має координати (6;9) .
1		2			9			6

Відповідь. А).

Частина друга

2.1.ОДЗ: 8x−20 0. 5 8x−20 =10, 8x−20 =2, 8x−20 =4, 8x =24, x =3.

Відповідь. 3.

2.2.	Оскільки точка A (−2;9) належить графіку функції y =ax2 +5x−7, то виконується рівність
	9=a (−2)2 +5 (−2) −7. 9=4a−10−7, звідки a =6,5.
	Відповідь. 6,5.
2.3.	Виразимо з першого рівняння системи y через x: y =9−2x2 . Підставимо значення y в дру-

ге рівняння системи і розв’яжемо його відносно x: 3x2 −2(9−2x2 ) =10, 3x2 −18+4x2 −10 =0, 7x2 −28 =0, x2 =4, x1 = −2, x2 =2. Тоді y1 =9−2 (−2)2 =1, y2 =9−2 22 =1.

Відповідь. (−2;1), (2;1) .

2.4.Нехай ABC — рівнобедрений трикутник ( AB = BC), AD — висота. BD =5 см, DC =8 см. Тоді BC = AB =13 см. З пря-

мокутного трикутника ABD: AD =			AB2 −BD2 =			132 −55 =12	D
							D
см. Площа трикутника S =	1	BC AD =		1	12 13 = 78	(см2).
см. Площа трикутника S =	2	BC AD =		2	12 13 = 78	(см2).	C
	2			2		A
Відповідь. 78 см2.						A
Відповідь. 78 см2.

ВАРІАНТ 6 19

Частина третя

3.1.Нехай швидкість руху першого автомобіля x км/год, а другого — (x+10) км/год. Систе матизуємо дані у вигляді таблиці.

Рух

s, км

v, км/год

t, год

Перший

450

автомобіль

Другий

450

x+10

450

автомобіль

x+10

Враховуючи, що другий автомобіль прибув у село на 30 хв =

год =

год швидше, ніж

перший, складаємо рівняння:

450

−

450

. ОДЗ: x ≠0, x ≠ −10.

x+10

450 2(x+10) −450 2x−x(x+10)

=0, x2 +10x−9000 =0, x1 =

−10−190

= −100 — не задоволь

2x(x+10)

няє умову задачі, x2 =

−10+190

=90.

Отже, швидкість руху першого автомобіля 90 км/год, а швидкість руху другого —

90+10 =100 км/год.

Відповідь. 90 км/год, 100 км/год.

y = −

3.2.

Проміжки зростання функції:

(−∞;−2 і

2;+ ∞), найбільше

значення функції: y = 4.

–8

–2

Відповідь. (−∞;−2

і 2;

+ ∞); 4.

–2

y = −

–4

3.3.

У прямокутній трапеції

ABCD

OF = OE = OK = OL = r,

CD = CE+ DE = 4+ 25 = 29 см.

За властивістю дотичних, проведених з однієї точки до кола, маємо: CF =CE =4 см, DK = DE =25 см. Проводимо

CM AD. KFCM — прямокутник, KM =CF =4 см, KF =CM.

Тоді DM = DK−KM =25−4 =21 см.

З прямокутного трикутника CMD CM = CD2 −DM2 = = 841−441 =20 см.

Тоді AB = CM = 20 см. За властивістю сторін описаного чотирикутника BC+ AD = AB+CD =20+29=49 см. Площа

трапеції S =	BC+ AD	CM =	49	20 =490 см2.
	2		2

B	F	C
			E
L	O
	O
A	K	M	D

Відповідь. 490 см2.

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015227.84 Кб2Doc1.doc
#
14.02.2015224.77 Кб2Doc2.doc
#
04.09.2019706.05 Кб1Dodatok_1.doc
#
15.02.201540.84 Кб4Dokument_Microsoft_Office_Word.docx
#
12.03.201615.72 Mб91dopatka_r_perepechko_a_kniga_o_sudah.pdf
#
15.02.20152.63 Mб44DPA_2011_mat-9-rozvyazannya-vsx-zavdan.pdf
#
06.11.2018148.48 Кб1dvp_pr_001.doc
#
14.02.2015318.98 Кб8Ekonomichna_istoriya_Ukrayini.doc
#
15.02.201556.71 Кб28ekonomika.docx
#
15.02.20151.71 Mб292Ekon_Pidp_ta_mij-komp-Fedorova.pdf
#
15.02.20151.04 Mб148Ekon_prom_pidpr_Maslak_2011.pdf