DPA_2011_mat-9-rozvyazannya-vsx-zavdan

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет кораблестроения им. адм. Макарова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Розв’язками нерівності є всі числа з проміжку

Розв’язками нерівності є всі числа з проміжку

.pdf

Скачиваний:

Добавлен:

15.02.2015

Размер:

2.63 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

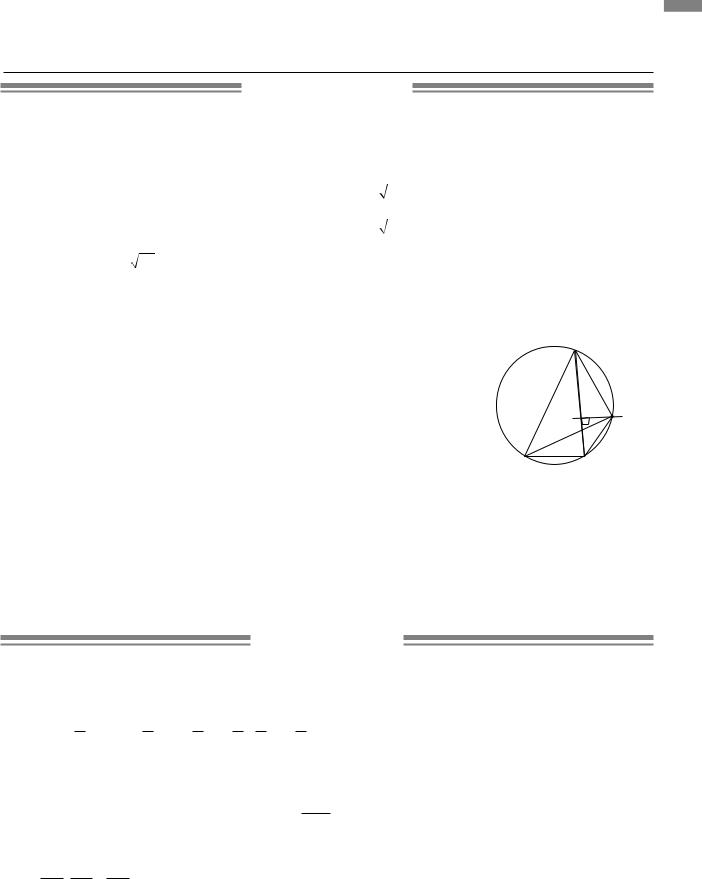
20 ВАРІАНТ 7

Частина четверта

4.1.М Запишемо рівняння (x+1)(x−1)(x−2)(x−4) =7 у вигляді (x2 −3x−4)(x2 −3x+2) =7.

Нехай x2 −3x−4 =t, тоді x2 −3x+2 =t+6.

Рівняння набуває вигляду t(t+6) =7 , t2 +6t−7 =0, звідки t =1 або t = −7.

3+ 29

x =

Маємо:

−3x−4 =1,

−3x−5 =0,

−3x−4 = −7;

−3x+3 =0;

3− 29

x =

Відповідь.

3±

4.2.М На рисунку зображено трикутник ABC, вписаний у коло.

Нехай бісектриса кута A перетинає коло в точці K.

За властивістю вписаних кутів, що спираються на одну

дугу, маємо: KCB = KAB =

, CBK = CAK =

Отже, KCB =CBK, тобто трикутник CBK рівнобед

рений з основою BC і CK = BK.

Проведемо серединний перпендикуляр до основи

рівнобедреного трикутника CBK.

Очевидно, що цей серединний перпендикуляр збігається

з прямою KN, якій належать висота, медіана й бісектриса

трикутника CBK.

Отже, серединний перпендикуляр до

сторони

перетинається з бісектрисою кута A в точці K, яка належить колу, описаному навколо трикутника ABC.

Варіант 7

Частина перша

1.1.3 год 24 хв = 3 60 хв + 24 хв = 180 хв + 24 хв = 204 хв.

Відповідь. В).

1.2.13−2 74 =13−2− 74 =11− 74 =10 77 − 74 =10 73 .

Відповідь. Г).

1.3.Відповідь. А).

1.4.Область визначення функції (−∞;+ ∞). x5−3 =0, якщо x = 3.

Відповідь. Б).

1.5.56m m32 = 25m .

Відповідь. В).

ВАРІАНТ 7 21

1.6.	−3a 3a = − (3a)2 3a = − 9a2 3a = − 27a3 .
	Відповідь. Б).
1.7. Відповідь. Г).
1.8.	Нехай 1500 грн — це 100 %. Тоді 1725 грн — це	1725 100	=115 %.
1.8.	Нехай 1500 грн — це 100 %. Тоді 1725 грн — це	1500	=115 %.
	Отже, 115 % – 100 % = 15 %.	1500
	Отже, 115 % – 100 % = 15 %.
	Відповідь. В).
1.9.	Відповідь. А).		B	C

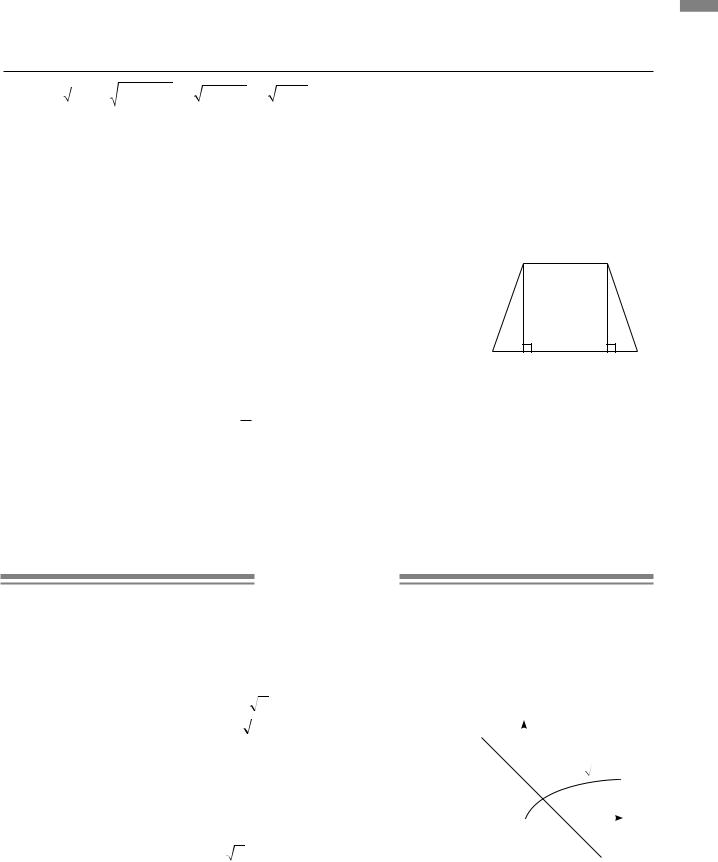
1.10.За умовою AM =4 дм, MD =16 дм. За властивістю рівнобічної трапеції KD = AM =4 дм.

Тоді BC = MK = MD−KD =16−4 =12 дм.
Відповідь. Б).	A	M	K	D
		M	K

1.11.Якщо тупий кут паралелограма дорівнює 150°, то гострий кут дорівнює 30°. Площа парале-

лограма S =10 15 sin30°=150 12 =75 (см2).

Відповідь. В).

1.12. AB2 =(1−(−2))2 +(2−y)2 =25, звідси 9+(2−y)2 =25, (2−y)2 =16, 2−y = −4 або 2−y =4, y = −2

або y =6.

Відповідь. Г).

Частина друга

2.1.ОДЗ: x ≠5, x ≠ −5.

	2(x+5) −4(x−5)	=	x2	+15	, 2x+10−4x+20 =x2 +15,	x2 +2x−15 =0, x = −5 (не належить ОДЗ),
	x2 −25	=	x2	−25	, 2x+10−4x+20 =x2 +15,	x2 +2x−15 =0, x = −5 (не належить ОДЗ),
	x2 −25		x2	−25		1
x2 =3.
Відповідь. 3.

2.2. Областю визначення функції y =					x є всі невід’ємні числа. Для
	побудови графіка функції			y =	x , скористаємося таблицею	:

	x	0	1	4	9

	y	0	1	2	3

	Графіком функції y =2−x є пряма, що проходить через
	точки (0;2) і (2;0) .
	Значення функції y = x				менше за значення функції

	y =2−x, якщо x	0;1).

)

Відповідь. 0;1 .

		y
y
=
2
	−
		x		y =	x
		x
2
2
1
1

		0	1 2			x

22	ВАРІАНТ 7

2.3.	Із співвідношення b6 =q2b4					знаходимо q2 =	b6	,	q2 =	4	, звідки q = −	2	= −	1	або q =	2	=	1	.
2.3.	Із співвідношення b6 =q2b4					знаходимо q2 =	b	,	q2 =	36	, звідки q = −	6	= −	3	або q =	6	=	3	.
							b			36		6		3		6		3
		1		1		4
	Відповідь. −	1	,	1	.
	Відповідь. −	3	,	3	.
		3		3

2.4.Нехай гіпотенуза трикутника дорівнює x см. Тоді невідомий катет дорівнює (x−8) см. За тео-

ремою Піфагора 122 +(x−8)2 =x2. 144+x2 −16x+64 =x2 , 16x =208, x =13. Тоді x−8 =13−8 =5 (см). P =12+5+13 =30 (см).

Відповідь. 30 см.

Частина третя

3.1.Нехай швидкість течії x км/год. Систематизуємо дані у вигляді таблиці.

						Рух													s, км										v, км/год												t, год

			За течією																30											18+x										30

																																									18+x
																																									18+x

		Проти течії																	16											18−x										16

																																									18−x
																																									18−x
						Враховуючи, що шлях туди і назад човен долає за 2,5 год =																														5	год, складаємо рівняння:
						Враховуючи, що шлях туди і назад човен долає за 2,5 год =																															год, складаємо рівняння:
			30								16		=	5		. ОДЗ: x ≠ −18, x ≠18.																2
			30				+				16			5
							+			18−x				2
		18+x								18−x				2
								30 2(18−x) +16 2(18+x) −5(18+x)(18−x)																					=0, 5x2			−28x+36 =0, x1 =						28−8	=2,
																																						28−8
																	2(18+x)(18−x)																					10
	x2 =				28+8							=3,6. Отже, швидкість течії 2 км/год або 3,6 км/год.
	x2 =				10							=3,6. Отже, швидкість течії 2 км/год або 3,6 км/год.
					10
	Відповідь. 2 км/год; 3,6 км/год.
3.2.									1						=								2n−1 − 2n+1							=			2n−1 − 2n+1				=
3.2.			2n−1 +									2n+1			=		( 2n−1 +						2n+1 )(			2n−1 −			2n+1 )	=			2n−1−(2n+1)				=
	= −			1		(			2n−1 −						2n+1 )				=	1		2n+1 −			1		2n−1 . Тоді заданий вираз можна записати у вигляді
	= −					(			2n−1 −						2n+1 )				=			2n+1 −			2		2n−1 . Тоді заданий вираз можна записати у вигляді
			2																2						2
1				3 −					1			1 +	1		5 −			1	3 +		1		7 −	1	5 +...+			1	121 −		1		119 = −	1	1 +		1	121 =		11		−	1	=5.
																																					2			2			2
2									2				2								2
2									2				2	2							2		2			2			2			2

Відповідь. 5.

3.3.У трикутнику ABC AB =CB, BD — висота,

BD = BO+OD =13+5 =18 см. OE =OD =5 см.

З прямокутного трикутника BOE:

BE =

BO2 −OE2 = 169−25 =12 см.

BDC BEO:

, BC = BO BD

BC =

13 18

=19,5 см, DC =

OE BD , DC =

5 18

=7,5 см.

AC =2DC =15 см. P =2BC+ AC =2 19,5+15 =54 см.

Відповідь. 54 см.

ВАРІАНТ 8 23

Частина четверта

4.1.М В одній системі координат побудуємо графіки рівнянь.

Графік рівняння

=2 — квадрат із вершинами

в точках: (2;0) , (0;2) , (−2;0)

і (0;−2).

Графік рівняння x2 +y2 =a2 — коло з центром у початку

координат і радіусом a (a > 0).

Система матиме чотири розв’язки, якщо коло і квадрат

–2

2 x

матимуть чотири спільні точки. Це можливо, коли коло впи-

сане у квадрат або описане навколо нього.

–2

Отже, a =2 або a =OA =

2 .

Відповідь. При a =2 або a = 2 .

4.2.М Нехай m , m , m — медіани трикутника, що проведені до сторін a, b і c

відповідно.

b c

За наслідком із теореми косинусів маємо:

4ma2 +a2 =2b2 +2c2,

4mb2 +b2 =2a2 +2c2,

4mc2 +c2 =2a2 +2b2

або

ma2 =

2b2 +2c2 −a2

mb2 =

2a2 +2c2 −b2

mc2 =

2a2 +2b2 −c2

Оскільки за умовою ma2 +mb2 =5mc2, то

2b2 +2c2 −a2 +2a2 +2c2 −b2

5(2a2 +2b2 −c2 )

b2 +4c2 +a2 =10a2 +10b2 −5c2 , 9c2 =9a2 +9b2 , c2 = a2 +b2 .

За теоремою, оберненою до теореми Піфагора, дістали, що трикутник прямокутний.

Варіант 8

Частина перша

1.1.Відповідь. Б).

1.2.52 : 101 = 25101 =4.

Відповідь. В).

1.3.16− p2 =42 − p2 =(4− p)(4+ p).

Відповідь. Г).

1.4.(a2 −2b)(b−3a2 ) =a2b−3a4 −2b2 +6a2b = −3a4 +7a2b−2b2 .

Відповідь. А).

1.5. Оскільки a3 a−3 = a3+(−3) = a0 =1≠ a, x5 :x6 =x5−6 =x−1 ≠ x, (a−2 )−3 =a−2 (−3) =a6, (x−2 )4 =x−2 4 =x−8 ≠ x8 ,

то рівність (a−2 )−3 =a6 є тотожністю.

Відповідь. В).

24	ВАРІАНТ 8

	2x−8 3x+6			2(x−4) 3(x+2)	6
1.6.			=		=		.
1.6.	x+2	x2 −16	=	(x+2)(x−4)(x+4)	=	x+4	.

Відповідь. Г).

1.7.Відповідь. Б).

1.8.Область визначення функції:

Звідси виплаває, що x =0.

Відповідь. В).

−x

x(x

−

x =0,

−x =0,

(−∞;1) (1;+ ∞).

=0, якщо

x2 =1,

−1

x−1≠0;

x ≠1;

x ≠1.

1.9.Оскільки (bd) і 2 вертикальні, то (bd) =60°. Оскільки (bd) і 1 є внутрішніми

односторонніми при паралельних прямих a і b і січній d, їх сума дорівнює 180°.

1=180°−60°=120°.

Відповідь. Б).

1.10.Шуканий центральний кут дорівнює 360° 13 =120°.

Відповідь. А).

1.11.Оскільки всі внутрішні кути правильного многокутника рівні, а їх сума дорівнює 180°(n−2),


то внутрішній кут при вершині правильного многокутника дорівнює							180°(n−2)	. При n =6
							n	. При n =6
	180°(6−2)						n
	180°(6−2)				=120°.
6					=120°.
6
Відповідь. Г).
1.12. S =		p r	=	24 4		=48 (см2).
1.12. S =			=	2		=48 (см2).
2				2

Відповідь. Г).

Частина друга

2.1.У чисельнику винесемо за дужки спільний множник 3, а знаменник розкладемо на множники,

12−6a+3a2

3(4−2a+a2 )

скориставшись формулою суми кубів двох чисел. Тоді

a3 +8

(a+2)(a2 −2a+4)

a+2

Відповідь.

a+2

2.2. Відомо, що ax2 +bx+c =a(x−x1 )(x−x2 ), де x1, x2 — корені квадратного тричлена.

−

x2 −x+6 =0, якщо x1 = −6, x2

=3. Тоді −

x2 −x+6 = −

(x+6)(x−3).

Відповідь.

−

(x+6)(x−3).

ВАРІАНТ 8 25

2.3.Дільниками числа 24 є числа 1, 2, 3, 4, 6, 8, 12, 14. Оскільки ймовірність події — це відношення кількості сприятливих подій до загальної кількості подій, то ймовірність того, що одне вибране з 24 чисел буде дільником числа 24, дорівнює P = 248 = 13 .

Відповідь. 13 .

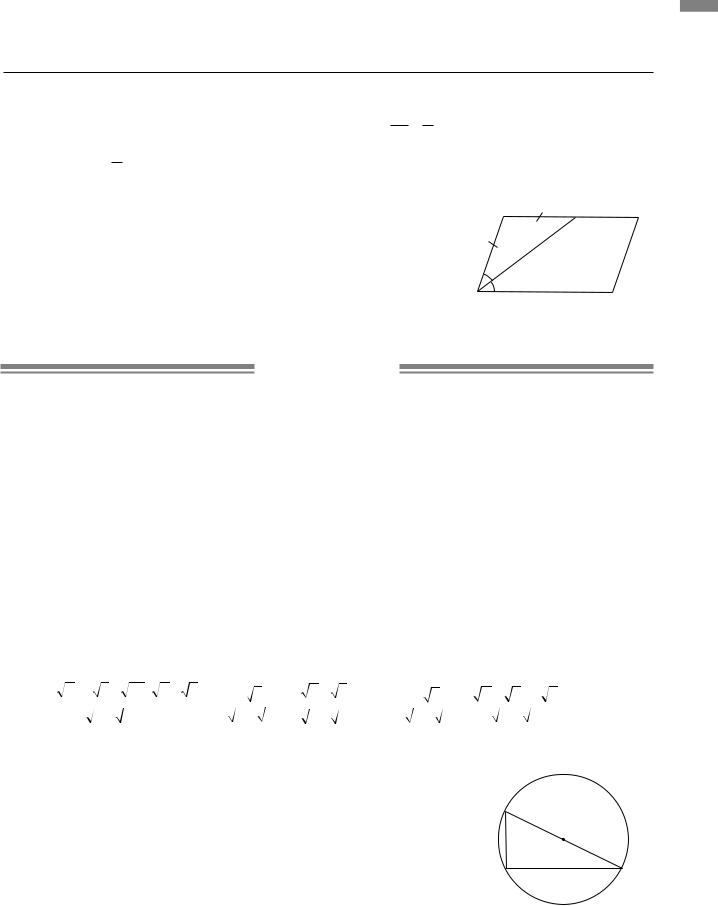
2.4. Відомо, що бісектриса кута A паралелограма ABCD відтинає				B	K	С
						С
на протилежній стороні відрізок, що дорівнює прилеглій
стороні.	Тоді AB = BK =3 см,	BC = BK+KC =3+2 =5	см.
Оскільки	протилежні сторони	паралелограма рівні,	то
P =2( AB+BC) =2(3+5) =16 (см).				A		D

Відповідь. 16 см.

Частина третя

3.1.Нехай перший робітник повинен за планом виготовити x деталей, а другий — y деталей. Систематизуємо дані у вигляді таблиці.

	І робітник			ІІ робітник		Кількість деталей

За планом	x			y		250

Фактично	x+0,1x =1,1x		y+ 0,15y = 115,y			280

Маємо систему рівнянь		x+y =250,		y =250−x,
Маємо систему рівнянь					=280.
		1,1x+115,y =280.		1,1x+115,y	=280.

1,1x+1,15(250−x) =280, −0,05x = −7,5, x =150. Отже, перший робітник за планом має виготовити 150 деталей, а другий — 250−150 =100 деталей.

Відповідь. 150 деталей, 100 деталей.

a a +b b − ab ( a +

(

a −

b )(a−b)

2 b

a − b +2 b

3.2.

b )

=1.

( a + b )(a−b)

(

b )(a−b)

a + b

a +

Відповідь. 1.

3.3. AC BC, точка C належить колу, тому AB — діаметр кола,
AB=2AO =2 10 =20 см.	A
За теоремою Піфагора AC2 +BC2 = AB2.		O
Нехай AC =x, тоді BC =x+4, тоді x2 +(x+4)2 =400,
x2 +4x−192 =0, x = −16 — не підходить за змістом задачі,	C	B
1	C
x2 = 12. Отже, AC =12 см, BC =12+4 =16 см.
Відповідь. 12 см, 16 см.

26 ВАРІАНТ 9

Частина четверта

4.1.М Оскільки x = 0

не є коренем рівняння

−

+3x+2

x2 +5x+2 24

то поділимо чисельник і знаменник дробів рівняння на x (x ≠ 0).

Дістали:

−

+3 x+

24t+48−24t−t2 −2t

Нехай x+

+ 3

= t, тоді рівняння набуде вигляду:

−

= 0,

= 0.

t+2

24t(t+2)

t2 + 2t− 48 = 0,

Це рівняння рівносильне системі: t ≠ 0,

t ≠ −2,

звідки маємо: t = −8

або t = 6.

−11± 113

x =

+ 3 = −8,

+11x+ 2 = 0,

Маємо:

− 3x+ 2 = 0;

x = 1,

+ 3 = 6; x

x =

Відповідь. 1; 2;

−11±

113

4.2.М Нехай h , h

і h

— висоти, що проведені до сторін a, b і c

трикутника відповідно.

Площа S цього трикутника дорівнює: S =

ah , або S =

bh , або S =

ch .

2 b

2 c

Маємо:

h =

, h =

h =

, тоді

2S a 2

2S b 2

a 2

b 2

= 1 (за умовою).

c 2S

Отже, a2 + b2 = c2

і за теоремою, оберненою до теореми Піфагора, трикутник прямокутний.

Варіант 9

Частина перша

1.1.Відповідь Г).

1.2.Нехай із 18 кг свіжих грибів отримають x кг сушених. Складаємо пропорцію 1812 = 1,x8 , звідки

x = 18 1,8 = 2,7. 12

Відповідь. Г).

ВАРІАНТ 9 27

1.3.Оскільки значення функції дорівнює 3, то −5+4x =3, звідки x =2.

Відповідь. Б).

1.4.(3a−b)(3a+b) +b2 =(3a)2 −b2 +b2 =9a2.

Відповідь. В).

1.5. − 16 + 81 − 121 = −4+9−11= −6.

Відповідь. Г).

1.6.0,25a5b4 0,4a−9b−3 =0,25 0,4a5+(−9)b4+(−3) =0,1a−4b.

Відповідь. Б).

1.7.Нехай 5000 грн — це 100 %. Тоді через рік вкладник отримає 115 % від 5000 грн, або

5000 1,15 =5750 грн.

Відповідь. А).

1.8.ОДЗ нерівності (−∞;+ ∞). (x−5)(x+3) =0, якщо x1 = −3, x2 =5.

( )( ) ( )

Отже, x−5 x+3 0, якщо x −∞;−3 5;+ ∞ .

Відповідь. Б).

+ – +

–3 5 x

1.9. Оскільки сума кутів трикутника дорівнює 180°, то K =180°−( M+ N) =180°− −(35°+25°) =120°. K — тупий, тому трикутник MNK — тупокутний.

Відповідь. Г).

1.10.Відповідь В).

1.11.Нехай M (x;y). Тоді x = 2+(2−6) = −2, y = −32+7 =2.

Відповідь. Б).

1.12. Радіус кола, вписаного в правильний шестикутник зі стороною a , дорівнює r = a 3 . Тобто

r =	4 3 3	=6 см.
	2

Тоді площа круга, обмеженого колом даного радіуса, S = πr2 =62 π=36π (см2).

Відповідь. Б).

Частина друга

a2 −b2

(a−b)(a+b)

a+b

2.1. Перетворимо вираз у дужках:

−

= −

b2 −ab

a2 −ab

b(b−a)

a(b−a)

ab(b−a)

Тоді

= −

a+b

= −1.

−ab

a+b

ab a+b

Відповідь. −1.

28 ВАРІАНТ 9

2.2.−1< 2−23x <2, −2<2−3x <4, −2<3x <4, − 23 <x < 43 .

Серед них цілими числами є 0 і 1.

Відповідь. 0; 1.

2.3.Графіком функції є парабола, вітки якої напрямлені вгору,

оскільки a =3 >0. Знайдемо координати вершини параболи:

x = −

= −

−12

=2,

y =3 22 −12 2+10 = −2.

Оскільки c =10,

2 3

парабола проходить через точку (0;10). Знайдемо точки пере-

тину графіка функції з віссю абсцис: 3x2 −12x+10 = 0, якщо

x1 =

6 −

; x2 =

6 +

Користуючись графіком, знаходимо

проміжок спадання функції: (−∞;2 .

Відповідь. (−∞;2 .

2.4. Нехай

ABCD

—

прямокутна трапеція,

AD =CD =12

см.

ADC =60°, CK

— висота трапеції. З прямокутного

три-

кутника

CKD:

KD =CDcosD =12cos60°=12

=6 (см). Тоді

AK = AD−KD =12−6 =6

(см). BC = AK =6

см. Середня лінія

MF =

BC+ AD

6+12

(см).

Відповідь. 9 см.

–2	x1	x2	x

A K D

Частина третя

3.1.Нехай запланована швидкість руху автомобіля x км/год. Систематизуємо дані у вигляді таблиці.

Рух

s, км

v, км/год

t, год

За планом

1200

Фактично

1200:3 = 400

800

x+ 20

400

800

x+20

Враховуючи, що на зупинку автомобіль витратив 2 год, складаємо рівняння:

400

800

+2 =

1200

. ОДЗ: x ≠ −20, x ≠0.

x+20

800x−800(x+20) +2x(x+20)

=0, x2 +20x−8000 =0, x1 =

−20−180

= −100 — не підходить

x(x+20)

за змістом задачі, x2 =

−20+180

=80. Отже, швидкість руху автомобіля до зупинки 80 км/год.

Відповідь. 80 км/год.

ВАРІАНТ 9 29

3−a+2a−2

−3a

a+1

−3a+a+1

3.2.

(a+1)(a

+3a)

−a+1

(a+1)

(a−1)

+1)(a+1)

(a+1) >0 при

a ≠ −1, отже,

при a ≠ −1.

(a+1)2

3.3.Кут DAF дорівнює куту BFA як внутрішні різносторонні при паралельних прямих AD і BC та січній AF. Кут BAF дорівнює куту DAF ( AF — бісектриса). Тому трикутник

BAF рівнобедрений з основою AF. BF = AB=3k, CF =4k,

тоді BF+CF =3k+3k =7k, 2( AB+BC) = P, 2(3k+7k) =80, k =4.

Отже, AB =3k =12 см, BC =7k =28 см.

Відповідь. 12 см; 28 см.

(a+1)(a−1)2		1
	=		.
(a−1)2 (a+1)(a+1)2		(a+1)2

A D

Частина четверта

4.1.М Побудуємо графік функції y = x2 −4 x +3 .

Спочатку побудуємо графік функції y =x2 −4x+3

при x 0.

Оскільки функція

y =x2 −4

парна, то її

y =

x2 −4

графік симетричний відносно осі

ординат.

Графікфункції y =x2 −4x+3,де x 0,відобразимо

відносно осі ординат.

y = 1

Для побудови графіка функції y =

x2 −4

ту

частину графіка функції, що міститься під віссю абсцис,

–3

–1

відобразимо відносно осі Ox.

Для того щоб рівняння

x2 −4

=a мало шість

розв’язків,

пряма y = a

повинна перетинати графік

функції y =

x2 −4

у шести точках, тобто a =1.

Відповідь. При a =1.

4.2.М Нехай на рисунку зображено трикутник ABC, у якому

AC =1 см, CB = 15 см, медіана CM дорівнює 2 см.

За наслідком із теореми косинусів маємо:

AB2 +(2CM)2 =2( AC2 +CB2 ), звідки

AB2 =2(1+15) −16 =16.

Дістали: AC2 +CB2 = AB2 , тобто трикутник ABC —

прямокутний із катетами AC і CB.

Площа трикутника ABC: S =

AC CB =

(см2).

Відповідь.

см2.

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015227.84 Кб3Doc1.doc
#
14.02.2015224.77 Кб2Doc2.doc
#
04.09.2019706.05 Кб1Dodatok_1.doc
#
15.02.201540.84 Кб4Dokument_Microsoft_Office_Word.docx
#
12.03.201615.72 Mб166dopatka_r_perepechko_a_kniga_o_sudah.pdf
#
15.02.20152.63 Mб44DPA_2011_mat-9-rozvyazannya-vsx-zavdan.pdf
#
06.11.2018148.48 Кб1dvp_pr_001.doc
#
14.02.2015318.98 Кб9Ekonomichna_istoriya_Ukrayini.doc
#
01.05.2025126.07 Кб0Ekonomichna_istoriya_Ukrayini.docx
#
15.02.201556.71 Кб30ekonomika.docx
#
15.02.20151.71 Mб305Ekon_Pidp_ta_mij-komp-Fedorova.pdf