Kuznecov_Praktikum

має підстав відкидати нульову гіпотезу. Якщо ж χ2спост буде більшим за χ2крит, то нульову гіпотезу слід відкинути і допустити альтернативу Н1: розподіл генеральної сукупності не відповідає нормальному закону.

2. Методичні вказівки

Лабораторну роботу розраховано на 2 години.

Завдання. Використовуючи інтервальний варіаційний ряд (див. роботу № 1), для вибірки А1 з рівнем значимості α перевірити гіпотезу про нормальний розподіл генеральної сукупності. Рівень значимості α взяти згідно з варіантом завдання (див. пояснювальну записку і таблицю).

Зразок виконання завдання

Виконуємо вказане вище завдання для вибірки A0 (див. табл.1.1) і рівня значимості α = 0,02. Скористаємось відповідним інтервальним варіаційним рядом (див. табл.1.3) і підрахованими в лабораторній роботі № 3 значеннями вибіркової середньої x =191,54 та середньоквадратичного відхилення σ =10,6.

Розрахунки, що пов'язані з обчисленням теоретичних частот і спостереженого значення χ2спост, зведемо до табл.5.1, другий і третій стовпці якої візьмемо з табл.3.1 (xi – середини інтервалів і ni – частоти, що відповідають кожному інтервалу). Три наступні стовпці по-

21

леннями) і f (ti) (значеннями функції щільності нормального розподілу, які у відповідності до значень аргументу знаходимо в таблиці дод.5).

Теоретичні частоти ni′ підраховуємо за співвідношенням

ni′ = nh f (ti ),

σ

де n – об'єм вибірки, n = 170; h – довжина інтервалу варіаційного ряду, h = 7.

містить цілі значення теоретичних частот нормального розподілу. В останньому стовпці обчислюємо відношення квадратів відхилень

Сума значень останнього стовпця цієї таблиці є шукане спостережене значення критерію: χ2спост ≈ 14,54.

Критичне значення критерію знаходимо за таблицею дод.4:

χ2крит(α, r) = χ2крит(0,02; 6) = 15,03.

Через те, що χ2спост < χ2крит, немає підстав відкидати нульову гіпотезу. Таким чином, при заданому рівні значимості α = 0,02 (тобто з

2%-м ризиком помилитися або з довірчою ймовірністю γ = 0,98) можна стверджувати, що генеральна сукупність розподілена за нормальним законом.

Лабораторна робота ¹ 6

КОРЕЛЯЦІЙНА ЗАЛЕЖНІСТЬ

1. Основні теоретичні відомості

Залежність між випадковими величинами X і Y може бути функціональною, статистичною і кореляційною.

Якщо кожному можливому значенню випадкової величини X

22

відповідає одне можливе значення випадкової величини Y, то кажуть, що існує функціональна залежність

Y = Y(X).

Статистичною називається залежність, при якій зі зміною однієї з випадкових величин випливає зміна закону розподілу другої випадкової величини.

Умовним середнім yx називається середнє арифметичне значення Y, що відповідає значенню X = x. Наприклад, при Х = 2 випадкова величина Y набувала значень 5, 6, 10; тоді умовне середнє зна-

5 + 6 +10 = 7. Аналогічно визначається умовне середнє xy.

3 Статистичну залежність називають кореляційною, якщо при зміні

однієї величини змінюється середнє значення другої величини. Отже, кореляційна залежність Y від X – це функціональна залежність умовної середньої yx від х, тобто

Рівняння (6.1) називається рівнянням регресії Y на Х, а графік функції f (x) – лінією регресії.

Аналогічно визначається кореляційна залежність Х від Y: xy = ϕ ( y).

Основними задачами теорії кореляції є встановлення форми кореляційної залежності, тобто вигляду функції регресії, та оцінка тісноти (сили) кореляційного зв'язку.

Якщо обидві функції f (x) і ϕ(y) лінійні, то кореляційну залежність (регресію) називають лінійною.

Тісноту кореляційного зв'язку між Х і Y можна оцінювати за величиною розсіяння значень y навколо умовних середніх yx і значень x навколо умовних середніх xy .

Припустимо, що в результаті n дослідів над випадковими величинами Х і Y одержано дані, згруповані у вигляді так званої кореляційної таблиці, де nij – частоти, які показують, скільки разів повторюється пара (xi, yj).

Якщо кореляційна залежність лінійна, то рівняння регресії Y на X має вигляд

23

де yx – умовна середня; x, y – вибіркові середні значення компонент Х і Y; σx, σy – вибіркові середньоквадратичні відхилення; rв – вибірковий коефіцієнт кореляції.

Для побудови рівняння (6.2) послідовно обчислюються значен-

ня:

Ті ж самі значення використовуються для запису рівняння регресії X на Y, яке має вигляд

xy − x = rв σσx ( y − y ). (6.3)

y

Одержане значення вибіркового коефіцієнта кореляції rв аналізують, використовуючи правило: чим ближче rв до 1, тим зв'я- зок між Х і Y тісніший.

24

2. Методичні вказівки

Лабораторну роботу розраховано на 4 години.

Завдання. Задано 100 пар значень випадкових величин Х і Y (кількісні ознаки 2 і 1 у вибірці А1).

1.За першими 20 парами Х і Y указаної вибірки побудувати кореляційне поле для Х, Y.

2.За заданою вибіркою скласти кореляційну таблицю для Х, Y.

3.Користуючись одержаною кореляційною таблицею, обчислити умовні середні і побудувати графіки емпіричної лінії регресії.

4.Використовуючи кореляційну таблицю, знайти лінійні функції регресії і побудувати їх графіки.

5.За вибірковим коефіцієнтом кореляції встановити тісноту зв'язку Х і Y.

Зразок виконання завдання

Виконуємо пункти вказаного завдання для наведеної нижче вибірки об'єму n = 90.

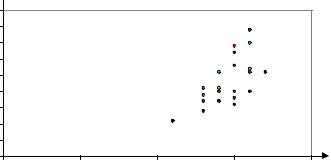
1.За останнім стовпцем заданих пар значень складаємо кореляційне поле для Х, Y (рис.6.1). Як бачимо, точки цього кореляційного поля знаходяться майже на прямій, отже, є рація шукати лінійну функцію регресії.

2.Складаємо інтервальну кореляційну таблицю (табл.6.1), вважаючи, що початок інтервалу входить до інтервалу, а кінець не входить.

3.Складемо кореляційну таблицю для середин інтервалів (табл.6.2). Одночасно обчислимо умовні середні однієї випадкової величини за умови, що друга випадкова величина зафіксована (розрахунок показано нижче), і в складеній таблиці добавимо один стовпець і один рядок для умовних середніх.

yx=14 = 64 3 + 74 15 + 84 14 = 83,44; 32

yx=16 = 74 7 + 84 16 + 94 11+104 1 = 85,71; 35

25

26

y

100

90

80

70

60

Після заповнення таблиці будуємо графіки емпіричної лінії регресії (рис.6.2).

4. Лінійні функції регресії знаходимо за формулами (6.2) і (6.3). Для цього послідовно обчислюємо:

27

вибіркові середні значення компонент X i Y:

+32 84 +14 94 + 9 104 +1 114 ) = 83,22;

середні значення квадратів компонент X i Y:

+14 942 + 9 1042 +1 1142 ) = 7057,56;

дисперсії й середньоквадратичні відхилення компонент X i Y:

σ2x = x2 − ( x )2 = 235,24 −15,222 = 3,53;

y

120

100

yx = f (x)

80

60

xy = ϕ( y)

40

Рис.6.2

28

так звану коваріацію компонент X i Y:

+ 2 18 84 + 3 18 94 + 7 18 104 +1 20 104 +1 20 114) = 1 (540 + 2304 + 90

+ 4440 + 2688 +15540 + ...+13104 + 2080 + 2280) = 115540 =1283,78;

Вибіркове рівняння прямої лінії регресії Y на Х згідно з (6.2)

yx − 83,22 = 0,8 11,47 ( x −15,22 ), 1,88

звідки yx = 4,88x +8,95.

Вибіркове рівняння прямої лінії регресії Х на Y згідно з (6.3)

xy −15,22 = 0,8 1,88 ( y − 83,22 ), 11,47

звідки xy = 0,13y+4,4.

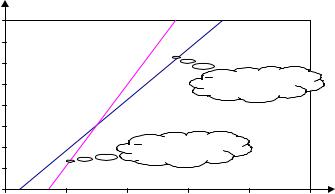
На завершення цього етапу роботи будуємо графіки прямих ліній регресії (рис.6.3).

5. Вибірковий коефіцієнт кореляції rв = 0,8 близький до одиниці. Отже, зв'язок між випадковими величинами Х і Y досить тісний,

29

Лабораторна робота ¹ 7

ОДНОФАКТОРНИЙ ДИСПЕРСІЙНИЙ АНАЛІЗ

1. Основні теоретичні відомості

Досліджується вплив деякого фактора Φ на величину певної кількісної ознаки X спостережуваної генеральної сукупності. Здійснюються декілька груп випробувань, кожна з яких відповідає певному рівню досліджуваного фактора. В загальному випадку розраховані при цьому групові середні відрізняються одне від одного. Дисперсійний аналіз дає змогу з'ясувати, чи мають розбіжності в групових середніх випадковий або достовірний та істотний характер.

Нехай задані вибірки Х1, Х2, …, Хp, які відповідають розглядуваним рівням фактора Φ1, Φ2, …, Φp. Потрібно за заданим рівнем

30