
Kuznecov_Praktikum
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Український державний морський технічний університет імені адмірала Макарова
ЛАБОРАТОРНИЙ ПРАКТИКУМ
З МАТЕМАТИЧНОЇ СТАТИСТИКИ
Рекомендовано Методичною радою УДМТУ
Миколаїв 2002

УДК 517:618.3
Кузнецов А.М., Зароський Р.І., Нєдєлько Є.Ю. Лабораторний практикум з математичної статистики. – Миколаїв: УДМТУ, 2002.
– 48 с.
Кафедра вищої математики
Наведено короткі теоретичні відомості, зразки завдань з докладними методичними вказівками про їх виконання, таблиці вихідних даних для варіантів завдань, таблиці стандартних статистичних розподілів та їх критичних значень.
Посібник може бути рекомендований до виконання лабораторних робіт у курсі математичної статистики, контрольних робіт з цього курсу на заочному відділенні тощо.
Рецензент канд. фіз.-мат. наук, доц. Т.А.Юрченко
Український державний морський технічний університет, 2002
Видавництво УДМТУ, 2002
2
ПОЯСНЮВАЛЬНА ЗАПИСКА
Виконання і захист лабораторних робіт є важливим етапом вивчення студентами курсу "Математична статистика". Кожний студент виконує ці роботи згідно з індивідуальним номером a свого варіанта, який він одержує від викладача.
За вказаним номером варіанта студент повинен сформувати індивідуальну статистичну сукупність даних, з якою він буде працювати під час виконання перших шести робіт. Основна сукупність даних кожного варіанта – вибірка А1 – це 100 пар значень двох кількісних ознак (ознака 1 – кількість балів, отриманих на тестуванні; ознака 2 – час, витрачений на підготовку до цього тестування). Вибірка А1 складається за наступним правилом: із таблиці дод.1 треба взяти 100 пар значень, починаючи з номера a і з номерами am = a + 5m (m = 0, 1, 2, …, 99). При цьому до значень обох ознак треба додати 0,1a і одержані таким чином значення округлити до цілого. Наприклад, для варіанта 31 вибірка А1 буде сформована збільшеними на три одиниці значеннями ознак з номерами 31, 36, 41, …, 526; результатом цього формування будуть наступні значення:
ознака 1 – 194, 83, 323, …, 284; ознака 2 – 28, 25, 44, …, 38.
У роботі № 4 використовується вибірка А2 з іншим, ніж у вибірки А1, об'ємом n = 20 + q, де q – остання цифра номера варіанта a (наприклад, для варіанта 31 n = 21).
Для виконання роботи № 7 вихідні дані наведено в дод.2; номер варіанта цих даних потрібно взяти такий же, як і вказане вище значення q – останньої цифри номера варіанта a. Усі вказані в таблицях дод.2 дані треба збільшити
на величину числа a. |
|
|
|
Необхідні для виконання |
Залишок від ділення a на 4 |
γ |
α |
робіт № 4 і 5 значення пара- |
0 |
0,80 |
0,10 |
метрів γ і α визначаються згід- |
1 |
0,90 |
0,05 |
но з номером варіанта із наве- |
2 |
0,95 |
0,02 |
деної таблиці. |
3 |
0,98 |
0,01 |
3

Лабораторна робота ¹ 1
ОПИС ТА СТАТИСТИЧНА ОБРОБКА ДАНИХ
1. Основні теоретичні відомості
Вся досліджувана сукупність об'єктів (кількістю N) називається
генеральною сукупністю.
Частина об'єктів кількістю n (n ≤ N), випадково відібрана з генеральної сукупності, називається вибірковою сукупністю, або вибіркою.
Нехай над випадковою величиною Х проведено n незалежних випробувань; х1, х2, …, хn – її можливі значення. Дані заносяться в наведену нижче таблицю в порядку їх одержання.
1 |
2 |
… |
i |
… |
n |
x1 |
x2 |
… |
xi |
… |
xn |
Цю таблицю називають статистичним рядом, а хі – варіантами. Серед варіант можуть бути однакові. Якщо кожній варіанті поставити у відповідність її частоту (кількість повторень) ni, а також
відносну частоту Pi* = ni , а самі варіанти записувати у зростаючо- n
му (спадаючому) порядку, то наведену нижче таблицю називають
варіаційним рядом.
X |
х1 |
х2 |
… |
хі |
… |
хk |
N |
n1 |
n2 |
… |
ni |
… |
nk |
P * |
P1* |
P2* |
… |
Pi* |
… |
Pk* |
Статистичною (емпіричною) функцією розподілу F *(x) випадкової величини Х називається закон зміни відносної частоти випадку X < x у даному статистичному матеріалі:
F *(x) = P*( X < x).
Якщо об'єм вибірки n великий, то доцільно весь інтервал одержаних значень хі розбити на часткові (як правило, рівні) інтервали
(х1, х2), (х2, х3), …,(хk, хk+1). Позначимо через ni число значень випадкової величини Х, які попали в інтервал (хі, хі+1). Припустимо,
4
що початок інтервалу входить в інтервал, а кінець – ні. Для кожно- |
||||||||
го інтервалу визначимо також відносну частоту P |
*. Наведена ниж- |
|||||||
|
|
|
|
|
|
i |
|
|
че таблиця, що була одержана в результаті цих дій, має називу гру- |
||||||||
пування або інтервального варіаційного ряду. |
|
|
|
|||||
I |
(x1, x2) |
(x2, x3) |
… |
(xi, xi+1) |
… |
(xk, xk+1) |
|
|
N |
n1 |
|
n2 |
… |
ni |
… |
nk |
|
P* |
P1* |
|
P2* |
… |
Pi* |
… |
Pk* |
|
Якщо на кожному з відрізків [хі, хі+1], взявши їх за основу, побу- |
||||||||
дувати прямокутник, площа якого дорівнює P*, то одержана фігу- |
||||||||
ра називається гісто- |
|
|
i |
|
|
|
||
|
|
|
|
|
|
|||
грамою (рис.1.1). Оче- |
|
Pi* / h |
|
|
|
|
|
|
видно, що її площа |
|
|
|
|
|
|
|
|
дорівнює одиниці. |
|
|
|
|
|
|
|
|
Вважаємо, що крок |
|
|
|
|
|
|
|
|
h = xi+1 – xi = const. |
|
|
|
f(х) |
|
|
||
|
|
|
|
|
|
|
||
|
х1 х2 х3 х4 х5 х6 х7 х8 х9 х10 х11 х12 х13 х14 х15 х16 |
х |
||||||
|
|
|
|
|
Рис.1.1 |
|
|
|
Якщо наближати |
h → 0, то гістограма буде все більш і більш |
|||||||
наближатися до деякої кривої, що обмежує площу, рівну одиниці. |
||||||||
Ця крива є графіком певної функції f (x), яку називають щільністю |
||||||||
розподілу випадкової величини Х. |
|
|
|
|
||||
|
|
|
2. Методичні вказівки |
|
|
|
||
Лабораторну роботу розраховано на 4 години.
Завдання. Задано вибірку A1 (див. пояснювальну записку і дод.1). Провести статистичну обробку сукупності значень ознаки 1. Побудувати:
1)варіаційний ряд;
2)інтервальний варіаційний ряд;
3)гістограму;
4)криву щільності розподілу;
5)статистичну функцію розподілу F *(x) і її графік.
5
Зразок виконання завдання
Виконуємо пункти вказаного вище завдання для наступної вибірки A0 об'єму n = 170 (табл.1.1).
Таблиця 1.1
187 |
193 |
199 |
197 |
196 |
184 |
200 |
193 |
198 |
191 |
193 |
188 |
193 |
195 |
197 |
199 |
202 |
193 |
190 |
197 |
195 |
182 |
201 |
202 |
184 |
197 |
205 |
178 |
191 |
200 |
223 |
188 |
192 |
188 |
194 |
183 |
207 |
183 |
195 |
184 |
175 |
195 |
212 |
197 |
194 |
184 |
175 |
198 |
189 |
194 |
185 |
213 |
192 |
200 |
194 |
173 |
206 |
163 |
204 |
174 |
183 |
199 |
203 |
185 |
199 |
196 |
196 |
188 |
169 |
196 |
190 |
205 |
189 |
189 |
190 |
175 |
190 |
193 |
209 |
190 |
183 |
191 |
193 |
191 |
190 |
192 |
191 |
185 |
202 |
173 |
184 |
176 |
199 |
182 |
186 |
189 |
193 |
185 |
168 |
192 |
193 |
205 |
171 |
193 |
191 |
206 |
187 |
193 |
192 |
189 |
191 |
190 |
182 |
194 |
194 |
197 |
207 |
198 |
180 |
175 |
193 |
191 |
188 |
187 |
191 |
191 |
192 |
192 |
214 |
171 |
208 |
185 |
195 |
190 |
214 |
193 |
183 |
193 |
193 |
187 |
198 |
203 |
181 |
173 |
189 |
195 |
180 |
180 |
205 |
194 |
179 |
191 |
201 |
195 |
195 |
189 |
185 |
199 |
194 |
187 |
173 |
211 |
190 |
165 |
182 |
182 |
194 |
168 |
176 |
192 |
– |
– |
– |
– |
– |
– |
– |
– |
– |
– |
1. Для впорядкування чисел ці дані можна подати графічно: на числовій осі відмічають результати вимірів, над кожним виміром точками відмічають, скільки разів зустрілося це число (рис.1.2).
n |
|
|
|
|
14 |
|
|
|
|
12 |
|
|
|
|
10 |
|
|
|
|
8 |
|
|
|
|
6 |
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
160 165 170 |
175 180 185 190 195 |
200 205 |
210 215 220 225 |
х |
Рис.1.2
6

Складаємо варіаційний ряд за цими даними (табл.1.2).
Таблиця 1.2
хі |
163 |
165 |
168 |
169 |
171 |
173 |
174 |
175 |
176 |
178 |
179 |
180 |
181 |
182 |
183 |
184 |
185 |
||||||||||||||||
ni |
1 |
|
1 |
2 |
1 |
2 |
4 |
1 |
4 |
2 |
1 |
|
1 |
3 |
2 |
4 |
6 |
5 |
6 |
||||||||||||||
xi |
186 |
187 |
188 |
189 |
190 |
191 |
192 |
193 |
194 |
195 |
196 |
197 |
198 |
199 |
200 |
201 |
202 |
||||||||||||||||
ni |
1 |
|
5 |
5 |
7 |
9 |
11 |
9 |
14 |
8 |
8 |
|
4 |
6 |
4 |
6 |
3 |
2 |
4 |
||||||||||||||
xi |
203 |
204 |
205 |
206 |
207 |
208 |
209 |
211 |
212 |
213 |
214 |
223 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
ni |
1 |
|
1 |
4 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
2. xmin = 163, xmax = 223, n = 170. Вибираємо крок h за формулою |
|||||||||||||||||||||||||||||||||
|
h = |
xmax |
− xmin |
; |
|
h = |
|
223 −163 |
= |
|
|
60 |
|
|
= 7,14. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
1+ 3,32lg170 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
1+ 3,32lgn |
|
|
|
|
|
1+ 3,32 2,23 |
|
|
|
|
|
|
|||||||||||||||||
Візьмемо h = 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. Одержуємо інтервальний варіаційний ряд (табл.1.3). |
|
|
|||||||||||||||||||||||||||||||
Таблиця 1.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ii |
|
163... |
170... |
|
177... |
|
184... |
191... |
|
198... |
205... |
|
212... |
|
|
219... |
|||||||||||||||||
|
…170 |
…177 |
…184 |
|
…191 |
…198 |
|
…205 |
…212 |
|
…219 |
|
…226 |
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ni |
|
5 |
|
13 |
|
|
17 |
|
38 |
60 |
|
21 |
|
11 |
|
|
4 |
|
|
1 |
|||||||||||||
P |
|
0,029 |
0,076 |
|
0,100 |
|
0,224 |
0,353 |
|
0,124 |
0,065 |
|
0,023 |
|
|
0,006 |
|||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
n |
0,004 |
0,011 |
|
0,014 |
|
0,032 |
0,050 |
|
0,018 |
0,009 |
|
0,003 |
|
|
0,001 |
|||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
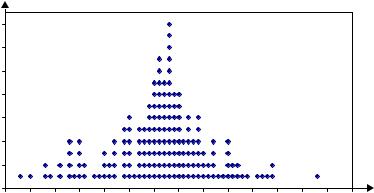
За одержаними даними складаємо гістограму (рис.1.3); краще це зробити на міліметровому папері.
4.Будуємо приблизну криву щільності статистичного розподілу f (x) (див. рис.1.3).
5.Знаходимо статистичну функцію розподілу F* (x):
F * (163) = 0; F * (170) = 0,029; |
F * (177) = 0,029 |
+ 0,076 = 0,105; |
F * (184 ) = 0,105 + 0,100 = 0,205; |
F * (191) = 0,205 + 0,224 = 0,429; |
|
F * (198) = 0,429+ 0,353 = 0,782; |
F * (205) = 0,782 |
+ 0,124 = 0,906; |
F * (212) = 0,906+ 0,065 = 0,971; |
F * (219) = 0,971 |
+ 0,023 = 0,994; |
F * (226) = 0,994 + 0,006 =1,00. |
|
|
7
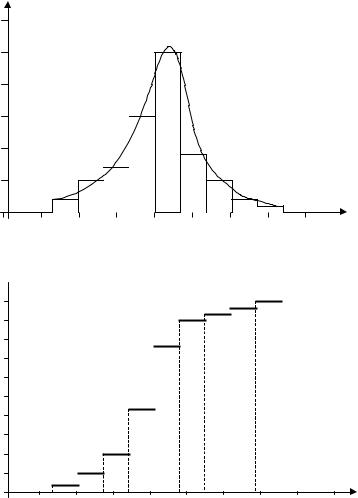
За цими даними будуємо графік статистичної функції розподілу |
|||||||||
F *(x) (рис.1.4). Як бачимо, він має ступінчатий (східчастий) харак- |
|||||||||
тер. |
|
|
|
|
|
|
|
|
|
P*/ h |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
0,06 |
|
|
|
|
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
|
|
0,04 |
|
|
|
|
|
|
|
|
|
0,03 |
|
|
|
|
|
|
|
|
|
0,02 |
|
|
|
|
|
|
|
|
|
0,01 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
x |
150 |
160 |
170 |
180 |
190 |
200 |
210 |
220 |
230 |
|
|
|
|
|
Рис.1.3 |
|
|
|
|
|
F* (x) 
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
160 |
170 |
180 |
190 |
200 |
210 |
220 |
230 |
240 |
х |
|
|
|
Рис.1.4 |
|
|
|
|
|
|
8
Лабораторна робота ¹ 2
ЧИСЛОВІ ХАРАКТЕРИСТИКИ ВИБІРКИ
1. Основні теоретичні відомості
До основних числових характеристик вибірки належать: вибіркове середнє (середнє арифметичне), дисперсія, середньоквадратичне відхилення, мода, медіана, коефіцієнт варіації.
Нехай над випадковою величиною проведено n випробувань, результатом яких є наведений нижче варіаційний ряд.
x1 |
x2 |
… |
xi |
… |
xk |
k |
n1 |
n2 |
|
ni |
|
nk |
∑ni = n |
… |
… |
i =1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вибіркове середнє x визначається за формулою
k
x = 1 ∑xi ni , (2.1) n i=1
де хі – варіанти; nі – відповідні частоти; k – кількість груп варіант; n – об'єм вибірки.
Якщо обчислення за формулою (2.1) громіздкі, то вводять так званий "хибний нуль" С. Значення С краще взяти рівним варіанті з максимальною частотою. Підрахунки у такому разі виконують за формулою
k
x = 1 ∑( xi −C )ni +C. (2.2) n i=1
Дисперсія вибірки σ2 обчислюється за однією з наступних формул:
k
σ2 = 1 ∑( xi − x )2 ni , (2.3) n i=1
k
σ2 = 1 ∑x12 ni −( x )2 , (2.4) n i=1
k
σ2 = 1 ∑( xi −C )2 ni −( x −C )2 . (2.5) n i=1
9

Середньоквадратичне відхилення вибірки σ визначається як квадратний корінь із дисперсії:
σ = σ2 . |
(2.6) |
Мода вибірки Мo для варіаційного ряду – це значення варіанти з максимальною частотою. Якщо задано інтервальний варіаційний ряд, то мода Мo обчислюється за такою наближеною формулою:
Mo = x0 |
+ h |
|
ns |
− ns−1 |
, |
(2.7) |
|
( ns |
− ns−1 )+ ( ns − ns+1 ) |
||||||
|
|
|
|
||||
де х0 – початок інтервалу з максимальною частотою (модальний інтервал); h – його довжина; ns – відповідна йому частота; ns–1 і ns+1 – частоти, що відповідають інтервалам попередньому і наступному за модальним.
Медіана вибірки Мe – це значення середнього елемента варіаційного ряду:
|
1 |
( xs |
+ xs+1 ), якщо n = 2s, |
|
|
2 |
|||
Me = |
|
|
(2.8) |
|
|
|
xs+1 , |
якщо n = 2s +1. |
|
|
|
|||
Для інтервального варіаційного ряду медіана Ме підраховується за формулою
Me = x |
|
+ h |
n /2 −Ts−1 |
, |
(2.9) |
|
0 |
ns |
|||||
|
|
|
|
|||
|
|
|
|
|
де х0 – початок медіанного інтервалу, тобто інтервалу, в якому утримується середній елемент; h – довжина медіанного інтервалу; n – об'єм вибірки; Тs–1 – сума частот інтервалів, які передують медіанному; ns – частота медіанного інтервалу.
Коефіцієнтом варіації вибірки V називають виражене у процентах відношення середньоквадратичного відхилення до вибіркового середнього:
V = |
|
σ |
|
100 %. |
(2.10) |
|
|
|
|
|
|||
|
|
x |
|
|
|
|
10
