- •Міністерство освіти і науки України
- •Теоретична частина
- •Комбінаційні схеми і цифрові автомати
- •Порядок виконання роботи
- •Контрольні запитання.
- •Теоретична частина Принципи побудови системи числення
- •Вибір системи числення
- •Загальні відомості про системи числення
- •Переведення чисел з однієї позиційної системи числення в іншу
- •Контрольні запитання.
- •Теоретична частина
- •Переведення чисел з однієї позиційної системи числення в іншу
- •Порядок виконання роботи
- •Контрольні запитання.
- •Теоретична частина Двійкова арифметика
- •В еом всі чотири арифметичні дії зводяться до дії додавання.
- •Порядок виконання роботи
- •Контрольні запитання.
- •Теоретична частина Від’ємні числа у форматі байта
- •Контрольні запитання.
- •Теоретична частина
- •Контрольні запитання.
- •Теоретична частина
Контрольні запитання.
Поясніть необхідність застосування в обчислювальній техніці двійково-десяткової системи числення.
Охарактеризуйте особливості кодування десяткових чисел прямим кодом 8-4-2-1 та кодом з надлишком 6.
Яким чином здійснюється переведення двійково-десяткових чисел у двійкові та навпаки?
Дайте означення триаді і тетраді.
Сформулюйте алгоритми переведення чисел з однієї системи числення в іншу.
|
Лабораторна робота № 7
| |
|
Тема: |
Виконання арифметичних дій в різних системах числення. Узагальнення та систематизація відомостей про системи числення.
|
|
Мета роботи:
Зміст роботи:
Організаційні та методичні вказівки: |
Набуття практичних навичок виконання арифметичних дій у системах числення, що застосовують в ЕОМ. Закріплення навичок користування можливостями калькулятора «Інженерний» стандартного офісного пакету MW для виконання арифметичних дій у системах числення з основою 2, 8, 16.
Повторення та систематизація теоретичних відомостей про арифметичні дії у системах числення з основою 2, 8, 16 та кодування від’ємних чисел. Застосування засобів Microsoft Windows для виконання арифметичних дій у двійковій, вісімковій та шістнадцятковій системах числення.
Лабораторну роботу проводять після вивчення розділу “Системи числення.” з підгрупою студентів у два етапи: 1. Підготовчий етап: Актуалізація опорних знань з теми “Системи числення. ” Повторення порядку виконання операцій над числами засобами калькулятора «Інженерний» стандартного офісного пакету MW. 2. Виконавчий етап: Виконання індивідуальних завдань. Перевірка правильності виконання дій за допомогою калькулятора «Інженерний» стандартного офісного пакету MW.
|
|
Технічне забезпечення: |
Персональний комп’ютер. |
|
Програмне забезпечення: |
Windows XP/7, Microsoft Excel. |
|
Час: |
80 хвилин.
|
Теоретична частина
Розглянемо, як іменуються числа в різних системах числення.
У десятковій системі числення використовуються наступні найменування для чисел і їх розрядів: одиниця, десяток, сотня, тисяча, мільйон, мільярд. У дванадцятковій системі числення також існують особливі назви для деяких розрядів чисел: одиниця, дюжина (одиниця другого розряду), гросс (одиниця третього розряду), фут (одиниця четвертого розряду). Кожен наступний розряд в 12 разів більше попереднього. Наприклад, число 276512 читається такі 2 фута, 7 гроссів, 6 дюжин і 5 одиниць.
Проте в більшості систем числення, з якими мають справу в кібернетиці, немає спеціальних назв для чисел і їх розрядів. Ми умовимося вимовляти найменування числа, називаючи підряд його цифри і основу системи числення.
Приклади
23114 -— читається: два три один один в системі з основою чотири.
16328 — читається: один шість три два в системі з основою вісім.
100112 — читається: один нуль нуль один один в системі з основою два.
У позиційних системах числення для запису будь-якого числа може бути використане тільки строго певна кількість введених цифр. У десятковій позиційній системі таких цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Якщо основа позиційної системи числення рівна q, то для запису будь-яких цілих і дробових чисел в цій системі числення досить q цифр, включаючи нуль.
Якщо q < 10, то ми умовимося використовувати вже відомі нам перші q цифр, вживаних у десятковій системі числення, а саме:
0, 1, 2, ..,, q-2, q-1.
Якщо q > 10, то як цифри використовуватимемо всі цифри десяткової системи і необхідну кількість нових цифр. Про те, які значки використовуватимуться як додаткові цифри, слід умовитися спеціально.
Виконайте вправи:
1. Перевірити, чи правильна наступна рівність:
а) 336 = 2110; у) 379= 2913; д) 456 = 110102;
б) 123 = 1012; г) 578 = 1425; е) 1327 = 6611.
2. Записати по два числа, попередні щодо кожного з даних і наступні за ним:
а) 2223; у) 10005; д) 30106;
б) 6107; г) 101002; є) АА01А11.
3. Знайти х і у з умов:
а) 23х = 32у; у) 24 х = 42 у; д) 144 х = 441 у;
6)51х = 15у; г) 23 х = 21 у; е)А9 х = 9А у.
4. Знайти основу системи числення з умов:
а) 4710 = 142 х у) 202 х = 13010; д) 89710 = 3ЕС х;
б) 103 х = 1910; г) 197110 = А0В х; е) 199010 = ВА1 х.
5. Як зміниться величина числа 3245, якщо:
а) до нього приписати справа нуль; два нулі;
б) до нього приписати зліва 3;
в) між цифрами 2 і 4 вписати цифру 0;
г) між цифрами 3 і 2 вписати цифру 1?
6. У спадаючій послідовності чисел деякі числа пропущені. Чому рівна основа системи числення? Впишіть пропущені числа в клітки наступного ряду:
641
644
646
650



7. Дане число 25638. У цьому числі викреслюється цифра «5» і замість неї вписується цифра «0». Стверджується, що нове число на 320 десяткових одиниць менше даного. Чи так це? Чому?
8. Довести, що число 144q, є повним квадратом; число 1ЗЗ1q є повним кубом. При яких q справедливі ці твердження?
Додавання і множення багатозначних чисел в недесяткових позиційних системах здійснюється за правилами складання і множення багатозначних десяткових чисел з обов'язковим обліком таблиць складання і множення цифр в даній системі. Таблиці складання і множення в десятковій арифметиці ми пам'ятаємо напам'ять, в інших же арифметиках ми заздалегідь складатимемо таблиці.
От як, наприклад, виглядають таблиці додавання в системах з основами q = 3 (табл. 1), q = 2 (табл. 2) і q = 5 (табл. 3) відповідно:
Таблиця 1
|
+ |
0 |
1 |
2 |
|
0 |
0 |
1 |
2 |
|
1 |
1 |
2 |
10 |
|
2 |
2 |
10 |
11 |
Таблиця 2
|
+ |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
1 |
10 |
Таблиця 3
|
+ |
0 |
1 |
2 |
3 |
4 |
|
0 |
0 |
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
10 |
|
2 |
2 |
3 |
4 |
10 |
11 |
|
3 |
3 |
4 |
10 |
11 |
12 |
|
4 |
4 |
10 |
11 |
12 |
13 |
Приклади
q=3;
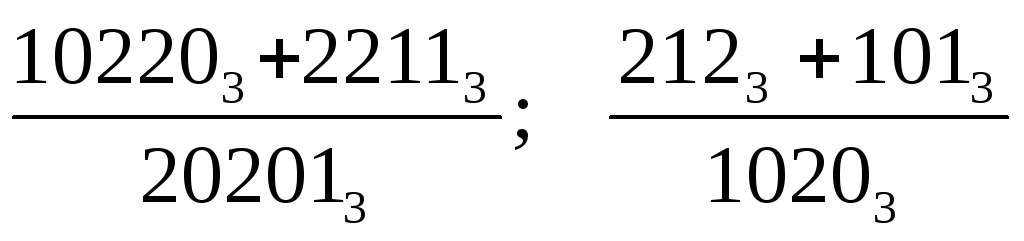
q=2;
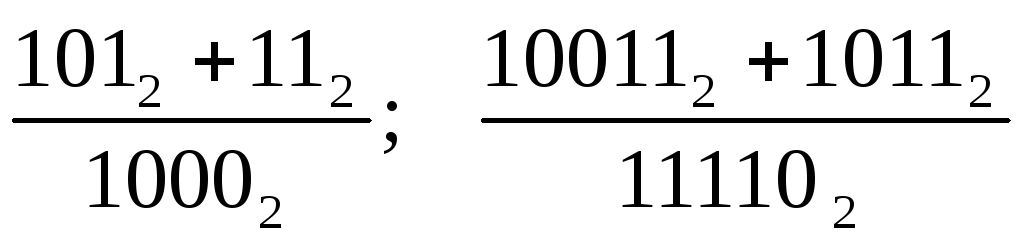
q=5;
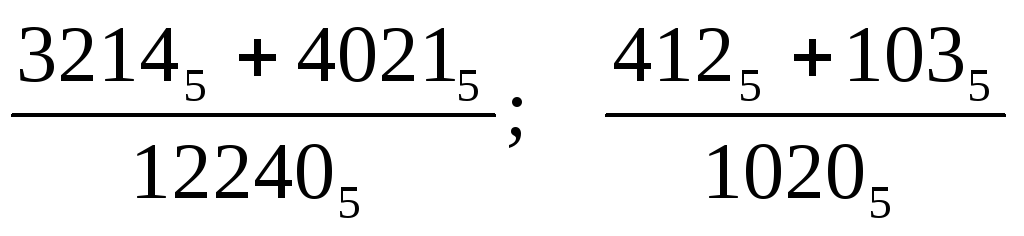
Виконайте дії:
1. Скласти таблицю додавання в системі числення з основою:
а) q=6; б) q=8; в) q=16.
2. Обчислити:
а) 2347+1237; е) 7DA016+18CB16;
б) 3015+1235+10025; ж) 10012+1112+10102;
в) 2034+13014+114; з) 1279+3169+4589;
г) 327658+75768; и) 35AF16+4D0E16;
д) АВ12+ВА12; к)110012+101112+10012
3. У яких системах числення одержані результати додавання?
а)
![]() б)
б)![]() в)
в)![]() г)
г)![]()
4. У якій системі числення проводилося додавання?
а)
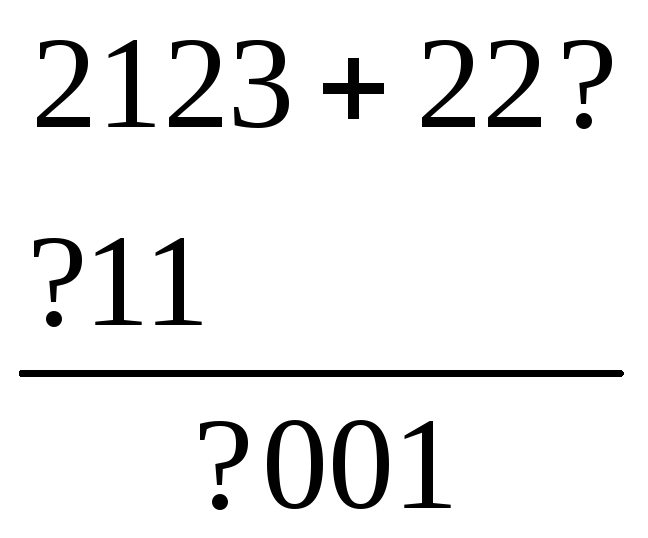 б)
б)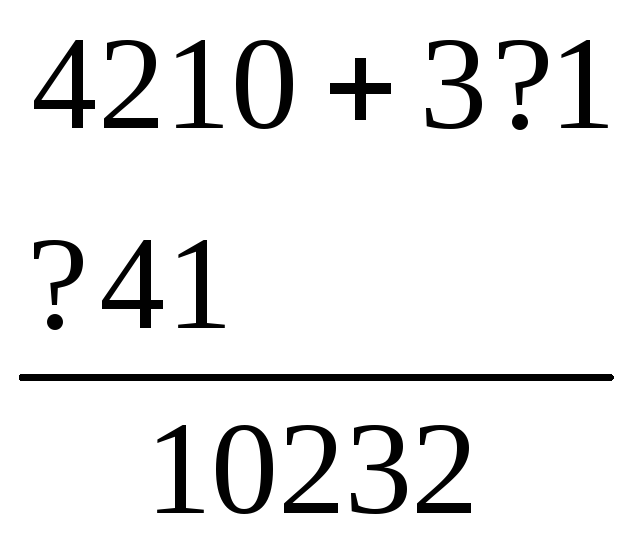 в)
в)
5. Скласти таблицю множення в системі числення з основою:
а) q=9; б) q=8;
6. Обчислити:
а)
![]() ; г)
; г)![]() ; ж)
; ж)![]() ;
;
б)
![]() ; д)
; д)![]() ; з)
; з)![]() ;
;
в)
![]() ; е)
; е)![]() ; і)
; і)![]() ;
;
к)
![]() ;
;
7. У якій системі числення виконувалося множення?
а)
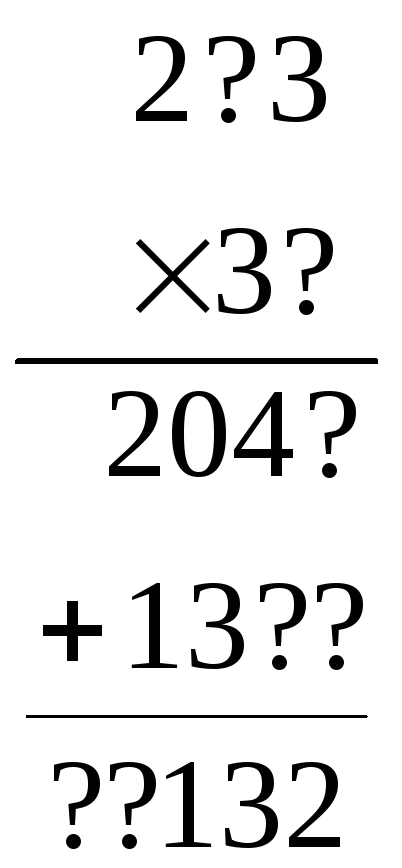 б)
б)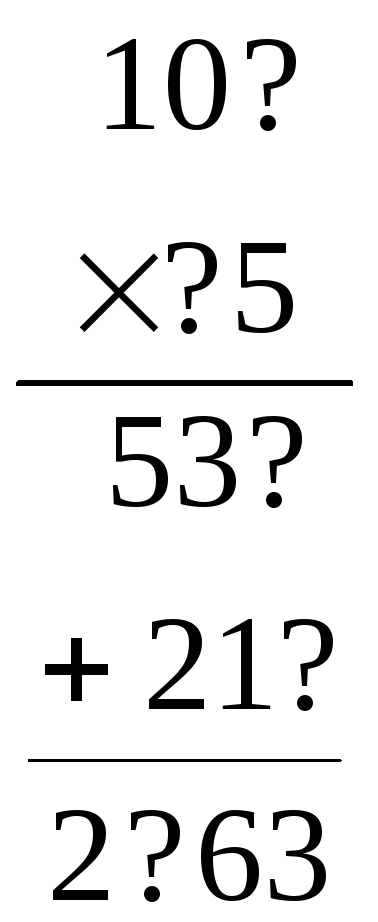
8. Обчислити:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
9. Відомо, що 23В>23А і 56В – 1 =56А, а також 179+1=17А. Використовуючи ці відомості, заповнити порожні клітки в наступних рядах:


10. Записати в многочленній формі наступні числа:
а)
![]() в)
в)![]() д)
д)![]()
б)
![]() г)
г)![]() е)
е)![]()
11. Яке з даних чисел збільшиться в 16 разів при перенесення коми управо на два знаки: 2,124; 11,24; 7810; 78416; 7,328?
12. Визначити, у якій системі числення проводилося додавання?
а)
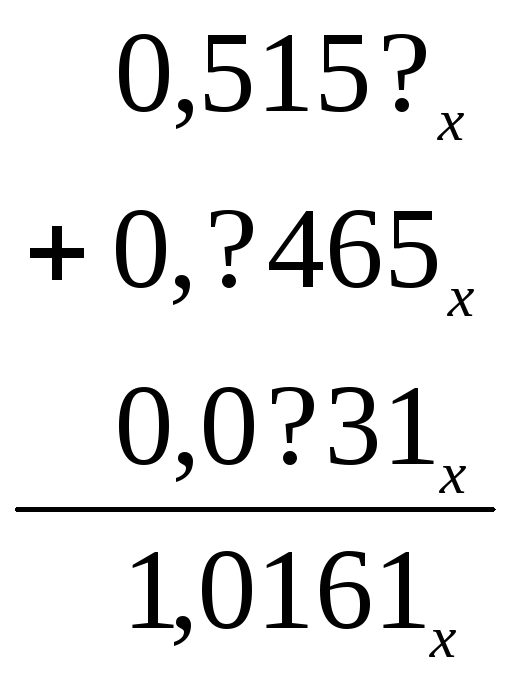 б)
б)