3.2.3. Емнісний елемент

Прикладом ємнісного елемента є плоский конденсатор – дві паралельні пластини, що перебувають на невеликій відстані одна від одної (рис. 3.6, а).

Нехай до ємнісного елемента прикладена напруга (рис. 3.6, б)

. (3.34)

На пластинах ємнісного елемента з'явиться заряд q, пропорційний прикладеній напрузі:

. (3.35)

Тоді струм у єм нісному елементі

Таким чином, одержимо важливі співвідношення:

Зіставляючи вираз (3.36) і (3.34), дійдемо до висновку: струм у ємнісному елементі випереджає по фазі напругу, прикладену до нього, на 90°.

Це положення ілюструється на рис. 3.6, в, г.

Аналіз виразів (3.36) і (3.38) дозволяє зробити й інші висновки:

• ємнісний елемент чинить синусоїдальному (змінному) струму опір, модуль якого Xс обернено пропорційний частоті.

• закон Ома виконується як для амплітудних значень струму й напруги:

, (3.39)

так і для діючих значень:

Виразимо миттєву потужність р через і :

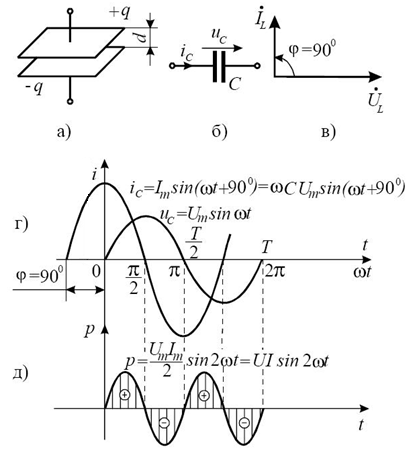
Рис. 3.6. Ємнісний елемент:

а) схема конструкції плоского конденсатора;

б) зображення ємнісного елемента на схемі;

в) вектори струму й напруги на ємнісному елементі;

г) графіки миттєвих значень струму й напруги;

д) графік миттєвої потужності.

Графік зміни потужності р з часом побудований на рис. 3.6, г. Аналіз графіка й (3.41) дозволяють зробити висновки:

- миттєва потужність на ємнісному елементі має тільки змін­ну (2.

- потужність періодично міняється за знаком - то позитивна, то негативна. Це значить, що протягом одних чвертьперіодів, коли р > 0, енергія запасається в індуктивному елементі (у вигляді енергії магнітного поля), а протягом інших чвертьперіодів, коли р < 0 енергія вертається в електричне коло. Енергія, що запасається в індуктивному елементі, за час dt дорівнює:

. (3.42)

Максимальна енергія, запасена в ємнісному елементі, визначиться по формулі:

З огляду на те, що , одержимо:

3.3 Розрахунок нерозгалуженого електричного кола синусоїдального струму

Для розрахунку режиму нерозгалуженого електричного кола застосуємо комплексний метод. Представимо всі синусоїдальні величини їхніми комплексами:

; ;

;

Порядок розрахунку такий же, як і на постійному струмі. По-перше, стрілками зображуємо позитивні напрямки струму, ЕРС і напруг. По-друге, вибираємо напрямок обходу контуру по напрямку руху годинникової стрілки й записуємо рівняння по другому закону Кірхгофа:

прояву закону Ома для резистивного, індуктивного і ємнісного елементів електричного кола:

; ; .

Тут множення на + j означає, що напруга випереджає по фазі струм на 90 , множення на - j означає, що напруга відстає по фазі від струму на 90°.

З (3.45) знаходимо комплексний струм у колі:

або (тому що )

де - напруга між виводами ab нерозгалуженого кола (рис. 3.7, а). Величина, що знаходиться в знаменнику,

називається комплексним опором нерозгалуженого кола.

Величина, зворотна комплексному опору, називається комплексною провідністю:

На рис. 3.7,б побудована векторна діаграма струму й напруг нерозгалуженого кола для випадку: .

Звичайно векторна діаграма будується наприкінці розрахунку за отриманим значенням струму й напруг. При цьому перевіряється правильність розрахунку.

Поділивши всі тридцятимільйонної векторної діаграми на, одержуємо значення комплексних опорів і зображуємо комплексні опори на комплексній площині (рис. 3.7, в) одержуємо діаграму, подібну до діаграми струму й напруг.

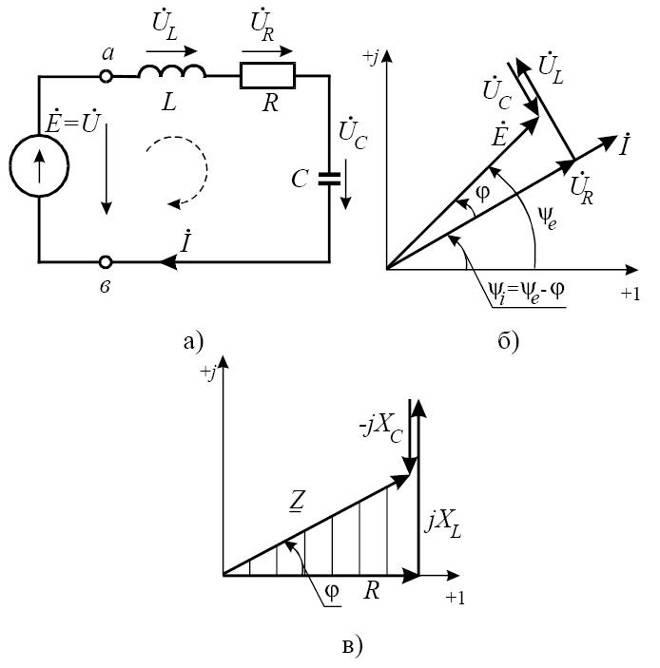
Рис. 3.7. Розрахунок нерозгалуженого електричного кола синусоїдального струму:

а) схема електричного кола;

б) векторна діаграма струму й напруг;

в) зображення комплексних опорів на комплексній площині.

Звернемо увагу на “трикутник опорів” (заштрихована площа), сторони якого відповідають опорам , і . Трикутник опорів подібний до трикутника напруг (рис. 3.7, б).

Аналіз діаграми опорів дозволяє перейти від алгебраїчної форми запису комплексного опору до тригонометричної й показової форм:

; (3.49)

, (3.50)

де - модуль комплексного опору або повний опір;

Залежно від знака величини аргумент комплексного опору може бути або позитивним (індуктивний характер), або негативним (ємнісний характер).

Підставивши (3.50) в (3.46) або в (3.47), одержимо закон Ома для нерозгалуженого кола:

Тобто

При декількох послідовно з'єднаних елементах комплексний опір

(3.54)

де - активний опір кола;

- реактивний опір кола.

В активному опорі відбувається необоротне перетворення електричної енергії в інші види енергії, а в реактивному опорі - не відбувається.

Повний опір і аргумент комплексного опору можна розраховувати по формулах:

, (3.55)