Лабораторная работа №6 Определение коэффициента вязкости жидкости

Студент должен знать:особенности молекулярного строения жидкостей; понятие идеальной и реальной жидкости, коэффициент вязкости и единицы его измерения; понятия ньютоновской и неньютоновской жидкостей; вывод формулы Пуазейля; гидравлическое сопротивление; распределение давления при течении жидкости по сосудам постоянного и переменного сечения; виды течения жидкости (ламинарное и турбулентное), число Рейнольдса, кинематическая вязкость; методы определения коэффициента вязкости (капиллярным медицинским вискозиметром, методом Стокса - с выводом формул); реологические свойства крови и особенности движения ее по сосудам.

Студент должен уметь:определять коэффициент вязкости жидкостей; оценивать погрешности измерений.

Краткая теория Предмет гидродинамики и реологии Уравнение Бернулли для идеальной жидкости

Актуальность изучения гидродинамики и в частности гемодинамики обусловлена, прежде всего, тем, что обеспечение жизнедеятельности тканей, органов связано с кровообращением. Нарушения в системе кровообращения, тромбозы являются причиной многих заболеваний. В нашей и многих других странах мира более 50% смертельных исходов связано с сердечно-сосудистыми заболеваниями (ишемическая болезнь сердца, головного мозга, конечностей, инфаркт миокарда, инсульт, гипертензии различной этиологии, диссеминированное внутрисосудистое свертывание крови и многие другие).

Жидкости занимают промежуточное положение между газами и твердыми телами. Жидкие среды составляют большую часть организма, поэтому изучение механических свойств и течения жидкостей является весьма актуальным для медицины.

В гидродинамике изучаются вопросы движения несжимаемой жидкости и взаимодействие их при этом с окружающими телами. Реальные жидкости малосжимаемы, поэтому можно говорить приблизительно об их несжимаемости.

Реологиейназывают учение о деформируемости и текучести вещества (в том числе и жидкости) и совокупность методов их исследования.

В гидро- и гемодинамике важным параметром является объемная скорость течения жидкости Q = V/t.

Для стационарного ламинарного течения идеальной (не имеющей внутреннего трения) и несжимаемой жидкости по трубам переменного сечения справедливо два основных уравнения гидродинамики:

1. Объемная скорость течения жидкости - уравнение неразрывности струи, где:υ- скорость жидкости,S - площадь сечения трубы.

2. -уравнениеБернулли, согласно которому полное давление жидкости одинаково во всех точках линии тока, где:-гидростатическое,P - статическое,- динамическое давления жидкости.

Вязкость жидкости

В реальной жидкости все закономерности течения жидкости усложняются вследствие наличия сил внутреннего трения - вязкости. При движении жидкости по трубе скорость различных слоев будет разной (рис.1). С наибольшей скоростью движутся слои в середине трубки, с наименьшей – слои, приближающиеся к стенке. Между слоями образуется градиент скорости: , где- расстояние между соседними движущимися слоями с разностью скоростей. Наличие градиента скорости обусловлено передачей количества движения от слоя к слою за счет сил трения между слоями. Согласно закону Ньютона градиент скорости пропорционален возникающим при этом силам внутреннего трения, действующим на единицу площади соприкасающихся слоев:, откуда сила внутреннего трения между слоями жидкости равна.

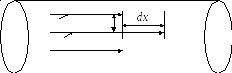
υ₂dυ

υ₁

Рис. 1.