3.7. Варианты заданий

№3.1. Найти интервалы монотонности следующих функций:

1. ;

2. ;

3. ;

4. на ;

5. .

№3.7.2. Исследовать на экстремум следующие функции:

1. ;

2. ;

3. ;

4. ;

5. .

№3.3. Исследовать на выпуклость и вогнутость следующие функции:

1. ;

2. ;

3. ;

4. ;

5. .

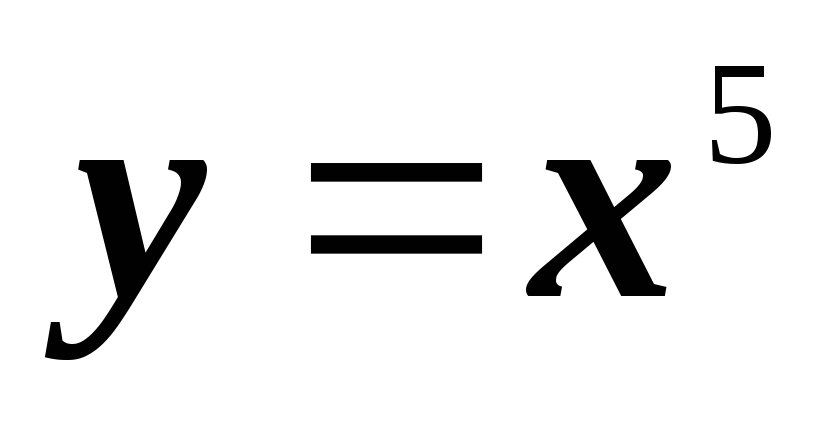№3.4. Найти наибольшее и наименьшее значения функции:

1. на отрезке ;

2. на отрезке ;

3. на отрезке .

№3.5. Исследовать функции и построить их графики:

1. y=3x⁵–5x³+2;

2. y=;

3. y=;

4. y=;

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

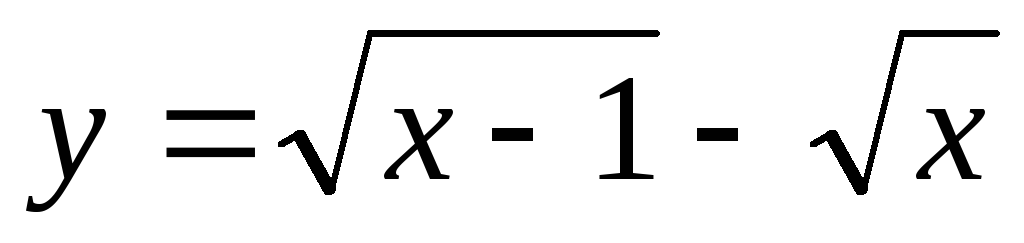
13. у = tg(x) – sin(x)

14. y = ctg(x) + cos(x)

3.8. Контрольные вопросы

1. Назовите основные пункты исследования графика функции.

2. Что называется областью определения функции?

3. Что называется областью значения функции?

4. Что является промежутками возрастания функции?

5. Что является промежутками убывания функции

6. Когда график функции имеет выпуклость?

7. Когда график функции имеет вогнутость?

8. Что называется асимптотами?

9. Какие бывают асимптоты?

10. Как найти асимптоты?

Глава 4. Функции нескольких переменных

4.1. Определение функции нескольких переменных

При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.

Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных. Обозначение z = f(x, y)

Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.

Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.

Окрестностью точки М₀(х₀, у₀) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию .

Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М₀(х₀, у₀), если для каждого числа  > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие , или условие.

Записывают:

4.2. Частные производные

Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение х к переменной х. Тогда величина _xz = f(x + x, y) – f(x, y) называется частным приращением функции по х.

Можно записать .

Тогда называетсячастной производной функции z = f(x, y) по х. Обозначение:

Аналогично определяется частная производная функции по у .

4.3. Полный дифференциал

Для функции f(x, y) выражение z = f(x + x, y + y) – f(x, y) называется полным приращением.

Выражение называетсяполным приращением функции f(x, y) в некоторой точке (х, у), где ₁ и ₂ – бесконечно малые функции при х  0 и у  0 соответственно.

Полным дифференциалом функции z = f(x, y) называется главная линейная относительно х и у часть приращения функции z в точке (х, у).

Для функции произвольного числа переменных:

4.5. Примеры

№1. Найти частные производные функций:

1. ;

2. ;

3. .

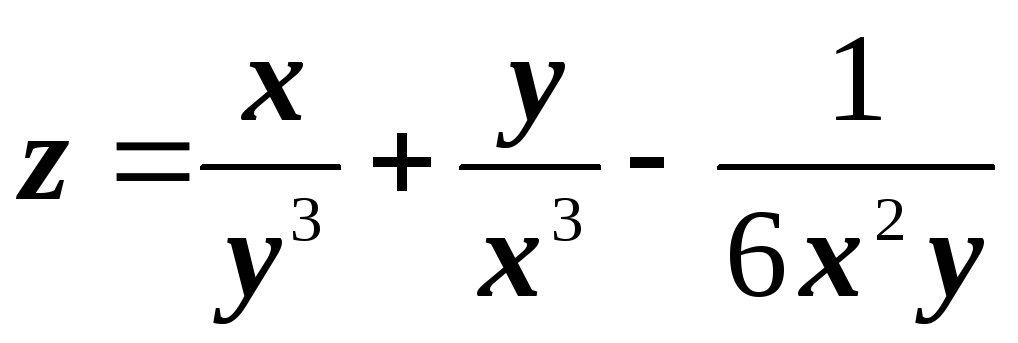Решение.

1. Частные производные функции двух и более переменных определяются по тем же формулам и правилам, что и функции одной переменной. Следует помнить только одно правило: если по одной переменной дифференцируем, то остальные считаются постоянными.

Имеем: (напомним, что ):

;

.

2. Воспользуемся правилом дифференцирования дроби:

;

.

3. Здесь имеем дело с производными сложной функции и дроби.

.

Ввиду симметрии выражения относительнох и у можно записать сразу

.

№2. Найти полный дифференциал функций:

1. ;

2. .

Решение.

1. Так как , то полный дифференциал имеет вид.

2. Вычислим частные производные по х, у, z

Таким образом, полный дифференциал