
- •Рязань 2012
- •Введение
- •Глава 1. Предел функции
- •1.1. Определение предела
- •1.2. Операции над пределами
- •1.3. Замечательные пределы
- •1.4. Примеры
- •1.5. Варианты заданий
- •1.6. Контрольные вопросы Глава 2. Производная и дифференциал
- •2.1 Понятие производной
- •2.2. Геометрический и физический смысл производной
- •2.3. Таблица производных
- •2.4. Основные правила дифференцирования
- •2.5. Производные высших порядков
- •2.6. Дифференциал функции
- •2.7. Геометрический смысл и свойства дифференциала
- •2.8. Дифференциалы высших порядков
- •2.9. Примеры
- •2.10. Варианты заданий
- •2.11. Контрольные вопросы
- •Глава 3. Исследование функций и построение графиков
- •3.1. Промежутки монотонности и знакопостоянства
- •3.2. Экстремумы функции
- •3.3. Выпуклость и вогнутость функции. Точка перегиба
- •3.4. Асимптоты
- •3.5.Общая схема исследования функции и построение графиков
- •3.6. Примеры
- •3.7. Варианты заданий
- •3.8. Контрольные вопросы
- •Глава 4. Функции нескольких переменных
- •4.1. Определение функции нескольких переменных
- •4.2. Частные производные
- •4.3. Полный дифференциал
- •4.5. Примеры
- •4.6. Варианты заданий
- •4.7. Контрольные вопросы Глава 5. Численное дифференцирование
- •5.1. Формулы для вычисления первой производной
- •5.2. Формулы второй производной
- •5.3. Примеры
- •5.4. Варианты заданий
- •5.5. Контрольные вопросы Глава 6 Основы интерполяции.
- •6.1. Постановка задачи
- •Интерполяционные формулы конечных разностей
- •6.3. Интерполяционные формулы центральных разностей
- •6.4. Интерполирование функции с не равноотстоящими узлами
- •6.5. Варианты заданий
- •6.6. Контрольные вопросы Глава 7. Неопределенный интеграл
- •7.1. Первообразная функция и неопределенный интеграл
- •7.2. Основные свойства неопределенного интеграла
- •7.3. Таблица простейших интегралов
- •7.4. Основные методы интегрирования
- •7.4.1. Непосредственное интегрирование
- •7.4.2. Метод подстановки (замена переменной)
- •7.4.3. Интегрирование по частям
- •7.5. Примеры
- •7.6. Варианты заданий
- •7.7. Контрольные вопросы
- •Глава 8. Определенный интеграл
- •8.1. Основные понятия и свойства определенного интеграла
- •Свойства определенного интеграла
- •8.2. Основные методы интегрирования
- •8.2.1. Формула Ньютона-Лейбница
- •8.2.2. Метод подстановки
- •8.2.3. Интегрирование по частям
- •8.3. Примеры
- •8.4. Варианты заданий
- •8.5. Биологические, физические и медицинские приложения определенного интеграла
- •8.5.1. Примеры задач прикладного характера.
- •8.5.2. Примеры решения задач.
- •8.5.3. Варианты заданий
- •Глава 9. Численное интегрирование
- •9.1. Формула прямоугольников
- •9.2. Формула трапеций
- •9.3. Метод средних
- •9.4. Формула Симпсона
- •9.5. Примеры
- •9.6. Варианты заданий
- •9.7. Контрольные вопросы
- •Глава 10. Дифференциальные уравнения
- •Основные определения
- •10.2. Уравнения с разделяющимися переменными
- •10.3. Однородные уравнения первого порядка
- •10.4. Линейные уравнения первого порядка
- •9.5. Примеры
- •I. Метод Лагранжа
- •II. Метод Бернулли
- •1) Метод вариации произвольной постоянной
- •2) Метод подстановки
- •10.6. Варианты заданий
- •10.7. Применение дифференциальных уравнений в биологии и медицине.
- •10.8. Варианты заданий
- •10.9. Контрольные вопросы
- •Глава 11. Численные методы решения дифференциальных уравнений
- •11.1. Метод Эйлера
- •10.2. Метод Рунге – Кутта
- •10.3. Примеры
- •11.4. Варианты заданий
- •11.4. Контрольные вопросы
- •Глава 12. Элементы теории вероятностей
- •12.1. Случайное событие
- •12.2. Комбинаторика
- •12.3. Вероятность случайного события
- •Закон сложения вероятностей
- •12.5. Варианты заданий
- •12.6. Условная вероятность, закон умножения вероятностей
- •12.7. Варианты заданий
- •12.8. Формулы полной вероятности и Байеса
- •12.9. Варианты заданий
- •11.10. Формулы Бернулли, Пуассона и Муавра-Лапласа
- •12.11. Варианты заданий
- •12.2. Случайные величины
- •12.2.1. Закон распределения случайной величины
- •12.2.2. Функция распределения случайных величин
- •12.2.3. Числовые характеристики дискретной случайной величины
- •12.2.4. Плотность вероятности непрерывных случайных величин
- •12.2.5. Нормальный закон распределения
- •12.3. Варианты заданий
- •Глава 13. Статистический анализ результатов исследований
- •13.1. Основные понятия математической статистики
- •13.1. Варианты заданий
- •13.2. Статистические оценки параметров распределения. Выборочные характеристики
- •13.2.1. Характеристики положения
- •13.2.2. Характеристики рассеяния вариант вокруг своего среднего
- •13.3. Варианты заданий
- •13.4. Оценка параметров генеральной совокупности по ее выборке
- •13.4.1. Точечная оценка параметров генеральной совокупности
- •13.5. Варианты заданий
- •13.6. Интервальная оценка параметров генеральной совокупности
- •13.7. Варианты заданий
- •1.8. Контрольные вопросы
- •Глава 14. Корреляционный и регрессионный анализ
- •14.1. Функциональная и корреляционная зависимости
- •14.2. Коэффициент линейной корреляции и его свойства
- •14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции
- •14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов
- •14.5. Нелинейная регрессия
- •14.6. Варианты заданий
- •Приложение
- •Критические значения выборочного коэффициента корреляции
- •Критерий Колмогорова – Смирнова Точные и асимптотические границы для верхней грани модуля разности истинной и эмпирической функции распределения
- •Распределение Пирсона (х2 – распределение)
- •Распределение Фишера – Снедекора (f-распределение)
- •Библиографический список
- •Содержание
- •Глава 13. Статистический анализ результатов исследований 150
- •Глава 14. Корреляционный и регрессионный анализ 168
3.3. Выпуклость и вогнутость функции. Точка перегиба
Опр. Кривая называется выпуклой на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая называется вогнутой на интервале (а, b), если все ее точки лежат выше любой ее касательной на этом интервале (рис. 3.5).

Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна (положительна), то кривая y = f(x) обращена выпукла (вогнута).
Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую.
Пусть кривая определяется уравнением y = f(x). Если вторая производная f(a) = 0 или f(a) не существует и при переходе через точку
х = а меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
3.4. Асимптоты
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.
Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Следует отметить, что не любая кривая имеет асимптоту. Асимптоты бывают вертикальные, наклонные и частный случай наклонных – горизонтальные.
Вертикальные асимптоты
Из
определения асимптоты следует, что
если![]() или
или![]() или
или![]() ,
то прямаях
= а
– вертикальная асимптота кривой y
= f(x).
,
то прямаях
= а
– вертикальная асимптота кривой y
= f(x).
Наклонные и горизонтальные асимптоты
Наклонная асимптота задается уравнением прямой y = kx + b, где коэффициенты k и b вычисляются по следующим формулам:
![]() ,
,
![]()
Если k =0, то получаем горизонтальную асимптоту.
3.5.Общая схема исследования функции и построение графиков
Графики функций строятся по точкам. Обычно из уравнения y=f(x) находят несколько точек графика функции y=f(x) и соединяют эти точки плавной кривой. Однако при таком методе легко пропустить какие-то важные особенности графика и допустить ошибку в построении.
Для построения графика функции нужно исследовать ее свойства. Процесс исследования функции состоит из нескольких этапов.
Область определения функции.
Координаты точек пересечения с осями координат.
Четность, нечетность функции.
Асимптоты графика и пределы на ±∞. (Если они имеются).
Критические точки.
Интервалы монотонности и точки экстремума.
Промежутки выпуклости и вогнутости, точки перегиба. (Если они имеются).
Дополнительные точки, если нет асимптот.
Построение графика.
Область значения функции.
3.6. Примеры
№1.
Исследовать функцию на монотонность
и экстремум
![]() .
.
Решение.
D(f)=R

 при
при
 ,
,
 ,
,
 .
.
–1,
![]() ,
1 – критические точки, так как внутренние
точки области определения и
,
1 – критические точки, так как внутренние
точки области определения и
![]() .
.
Выясним знаки производной:

Функция y=f(x) возрастает на промежутках (–∞; 1/5]; [1;+∞).
Функция y=f(x) убывает на промежутке [1/5; 1].
![]() –точка
максимума, f(
–точка
максимума, f(![]() )
– максимум функции.
)
– максимум функции.
1 – точка минимума, f(1) – минимум функции (рис. 3.6.1).

№2.
Исследовать функцию на выпуклость и
вогнутость. Найти точки перегиба:
![]() .
.
Решение.
D(f)=R
 .
.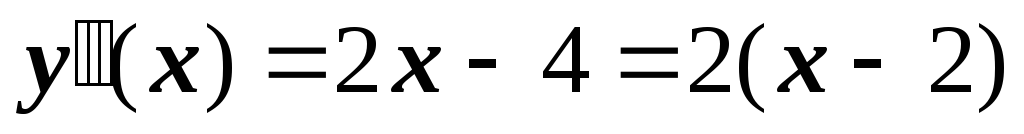 .
.
![]() при
при
![]() .
.

Функция y=f(x) выпуклая на промежутке (–∞; 2].
Функция y=f(x) вогнутая на промежутке [2; +∞).
(2;–1) – точка перегиба.
№3. Найти вертикальные асимптоты линии:
y=tgx;
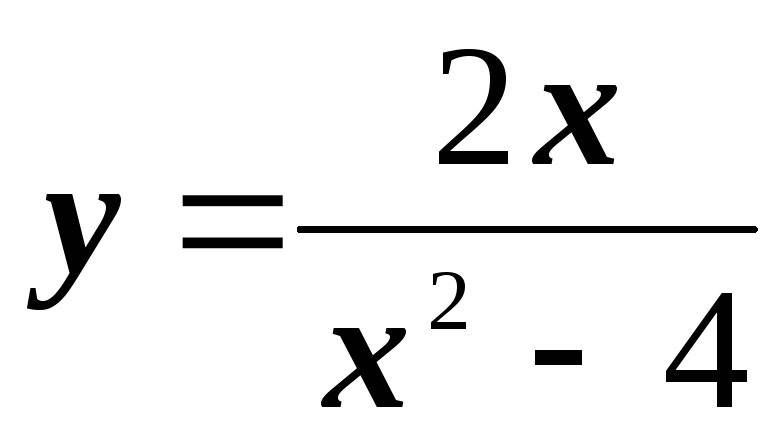 .
.
Решение.
Так как данная функция имеет разрыв в точках x=
 ,
то
,
то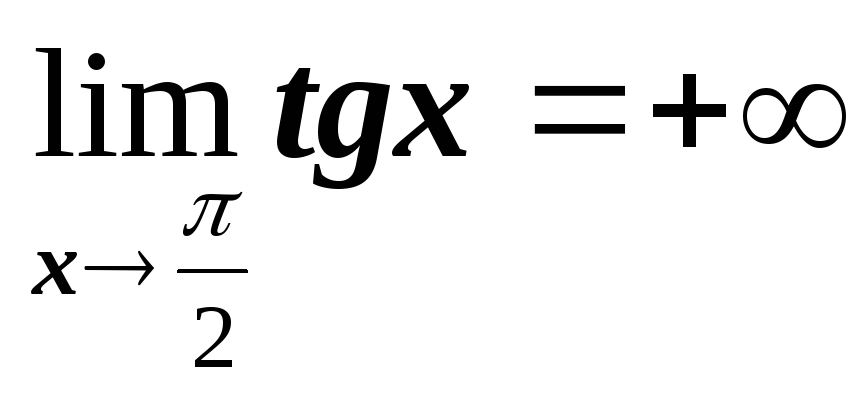 ,
, .
.
Следовательно,
![]() ,
,![]() – вертикальные асимптоты.
– вертикальные асимптоты.
Функция
 имеет бесконечный предел прих2
и х-2.
имеет бесконечный предел прих2
и х-2.

Значит,
прямые х=2
и х=
-2
(АВ и А′В′ на рис. 3.6.2) – асимптоты.
Прямая АВ служит асимптотой для двух
ветвей, UV
и KL.
Вдоль первой бесконечное удаление
направлено вверх, вдоль второй – вниз
(ибо
![]() и
и![]() .
Аналогично для прямой А′В′.
.
Аналогично для прямой А′В′.
Заметим, что прямая х=0 служит горизонтальной асимптотой (для ветвей UV и U′V′).
№4.
Исследовать
функцию
![]() и
построить ее график.
и
построить ее график.
Решение.
Находим область определения функции: (–; –1) (–1; 1) (1; ).
Точки пересечения с осью ОХ: у=0, тогда
![]() ,
,
х=0, => (0; 0) – точка пересечения с осью ОХ.
Точки пересечения с осью ОУ: х=0, тогда
![]() ,
,
у=0, => (0; 0) – точка пересечения с осью ОУ.
Область определения симметрична относительно нуля
![]()
Таким образом, функция является нечетной.
Так как точки х = 1, х = –1 являются точками разрыва, то вычислим следующие пределы:

Значит х = 1, х = –1 – вертикальные асимптоты.
Теперь найдем наклонные асимптоты.


Итого, уравнение наклонной асимптоты – y = x.
Находим критические точки.
Найдем производную функции
![]()
Критические
точки: x
= 0; x
= –![]() ;
x
=
;
x
=
![]() ;
x
= –1; x
= 1.
;
x
= –1; x
= 1.
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
x
< –![]() ,
y
> 0, функция возрастает
,
y
> 0, функция возрастает
–![]() < x
< –1, y
< 0, функция убывает
< x
< –1, y
< 0, функция убывает
–1 < x < 0, y < 0, функция убывает
0 < x < 1, y < 0, функция убывает
1
< x
<
![]() ,
y
< 0, функция убывает
,
y
< 0, функция убывает
![]() < x,
y
> 0, функция возрастает
< x,
y
> 0, функция возрастает
Видно,
что точка х
= –![]() является точкой максимума,
а точка х
=
является точкой максимума,
а точка х
=
![]() является точкой минимума.
Значения функции в этих точках равны
соответственно: –
является точкой минимума.
Значения функции в этих точках равны
соответственно: –
![]() и
и
![]() .
.
Найдем вторую производную функции
![]()
![]()
![]()
![]() .
.
Определим выпуклость и вогнутость кривой на промежутках.
x < –1, y < 0, кривая выпуклая
–1 < x < 0, y > 0, кривая вогнутая
0 < x < 1, y < 0, кривая выпуклая
1 < x, y > 0, кривая вогнутая
–1, 0, 1 – точки перегиба.
Построим график функции:
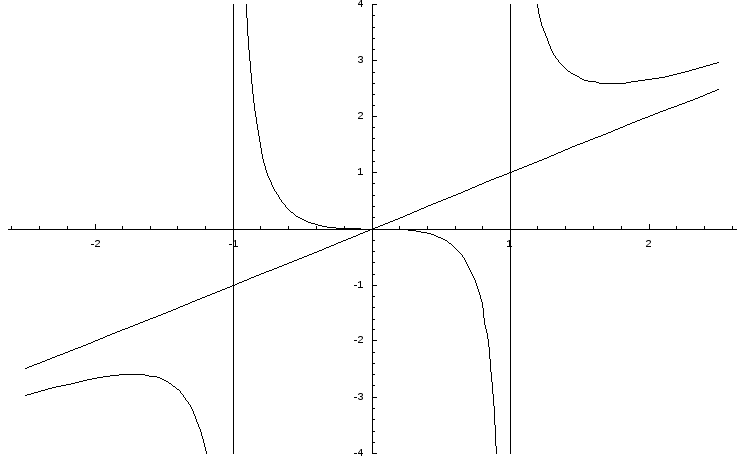
Рис. 3.8
.
Область значения E(y)=R.
