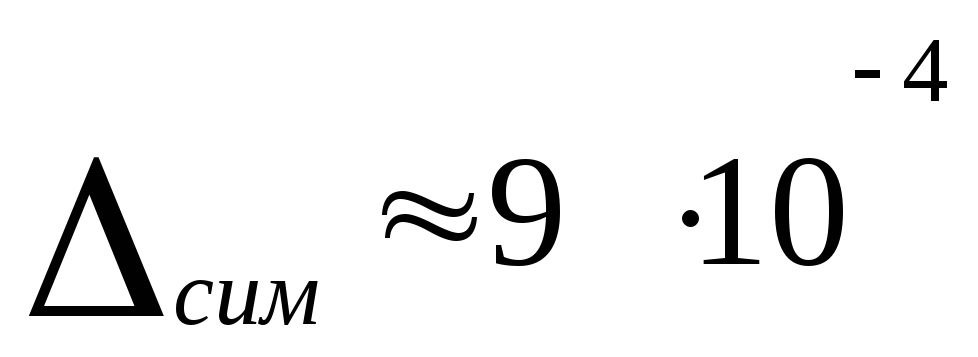- •Рязань 2012
- •Введение
- •Глава 1. Предел функции
- •1.1. Определение предела
- •1.2. Операции над пределами
- •1.3. Замечательные пределы
- •1.4. Примеры
- •1.5. Варианты заданий
- •1.6. Контрольные вопросы Глава 2. Производная и дифференциал
- •2.1 Понятие производной
- •2.2. Геометрический и физический смысл производной
- •2.3. Таблица производных
- •2.4. Основные правила дифференцирования
- •2.5. Производные высших порядков
- •2.6. Дифференциал функции
- •2.7. Геометрический смысл и свойства дифференциала
- •2.8. Дифференциалы высших порядков
- •2.9. Примеры
- •2.10. Варианты заданий
- •2.11. Контрольные вопросы
- •Глава 3. Исследование функций и построение графиков
- •3.1. Промежутки монотонности и знакопостоянства
- •3.2. Экстремумы функции
- •3.3. Выпуклость и вогнутость функции. Точка перегиба
- •3.4. Асимптоты
- •3.5.Общая схема исследования функции и построение графиков
- •3.6. Примеры
- •3.7. Варианты заданий
- •3.8. Контрольные вопросы
- •Глава 4. Функции нескольких переменных
- •4.1. Определение функции нескольких переменных
- •4.2. Частные производные
- •4.3. Полный дифференциал
- •4.5. Примеры
- •4.6. Варианты заданий
- •4.7. Контрольные вопросы Глава 5. Численное дифференцирование
- •5.1. Формулы для вычисления первой производной
- •5.2. Формулы второй производной
- •5.3. Примеры
- •5.4. Варианты заданий
- •5.5. Контрольные вопросы Глава 6 Основы интерполяции.
- •6.1. Постановка задачи
- •Интерполяционные формулы конечных разностей
- •6.3. Интерполяционные формулы центральных разностей
- •6.4. Интерполирование функции с не равноотстоящими узлами
- •6.5. Варианты заданий
- •6.6. Контрольные вопросы Глава 7. Неопределенный интеграл
- •7.1. Первообразная функция и неопределенный интеграл
- •7.2. Основные свойства неопределенного интеграла
- •7.3. Таблица простейших интегралов
- •7.4. Основные методы интегрирования
- •7.4.1. Непосредственное интегрирование
- •7.4.2. Метод подстановки (замена переменной)
- •7.4.3. Интегрирование по частям
- •7.5. Примеры
- •7.6. Варианты заданий
- •7.7. Контрольные вопросы
- •Глава 8. Определенный интеграл
- •8.1. Основные понятия и свойства определенного интеграла
- •Свойства определенного интеграла
- •8.2. Основные методы интегрирования
- •8.2.1. Формула Ньютона-Лейбница
- •8.2.2. Метод подстановки
- •8.2.3. Интегрирование по частям
- •8.3. Примеры
- •8.4. Варианты заданий
- •8.5. Биологические, физические и медицинские приложения определенного интеграла
- •8.5.1. Примеры задач прикладного характера.
- •8.5.2. Примеры решения задач.
- •8.5.3. Варианты заданий
- •Глава 9. Численное интегрирование
- •9.1. Формула прямоугольников
- •9.2. Формула трапеций
- •9.3. Метод средних
- •9.4. Формула Симпсона
- •9.5. Примеры
- •9.6. Варианты заданий
- •9.7. Контрольные вопросы
- •Глава 10. Дифференциальные уравнения
- •Основные определения
- •10.2. Уравнения с разделяющимися переменными
- •10.3. Однородные уравнения первого порядка
- •10.4. Линейные уравнения первого порядка
- •9.5. Примеры
- •I. Метод Лагранжа
- •II. Метод Бернулли
- •1) Метод вариации произвольной постоянной
- •2) Метод подстановки
- •10.6. Варианты заданий
- •10.7. Применение дифференциальных уравнений в биологии и медицине.
- •10.8. Варианты заданий
- •10.9. Контрольные вопросы
- •Глава 11. Численные методы решения дифференциальных уравнений
- •11.1. Метод Эйлера
- •10.2. Метод Рунге – Кутта
- •10.3. Примеры
- •11.4. Варианты заданий
- •11.4. Контрольные вопросы
- •Глава 12. Элементы теории вероятностей
- •12.1. Случайное событие
- •12.2. Комбинаторика
- •12.3. Вероятность случайного события
- •Закон сложения вероятностей
- •12.5. Варианты заданий
- •12.6. Условная вероятность, закон умножения вероятностей
- •12.7. Варианты заданий
- •12.8. Формулы полной вероятности и Байеса
- •12.9. Варианты заданий
- •11.10. Формулы Бернулли, Пуассона и Муавра-Лапласа
- •12.11. Варианты заданий
- •12.2. Случайные величины
- •12.2.1. Закон распределения случайной величины
- •12.2.2. Функция распределения случайных величин
- •12.2.3. Числовые характеристики дискретной случайной величины
- •12.2.4. Плотность вероятности непрерывных случайных величин
- •12.2.5. Нормальный закон распределения
- •12.3. Варианты заданий
- •Глава 13. Статистический анализ результатов исследований
- •13.1. Основные понятия математической статистики
- •13.1. Варианты заданий
- •13.2. Статистические оценки параметров распределения. Выборочные характеристики
- •13.2.1. Характеристики положения
- •13.2.2. Характеристики рассеяния вариант вокруг своего среднего
- •13.3. Варианты заданий
- •13.4. Оценка параметров генеральной совокупности по ее выборке
- •13.4.1. Точечная оценка параметров генеральной совокупности
- •13.5. Варианты заданий
- •13.6. Интервальная оценка параметров генеральной совокупности
- •13.7. Варианты заданий
- •1.8. Контрольные вопросы
- •Глава 14. Корреляционный и регрессионный анализ
- •14.1. Функциональная и корреляционная зависимости
- •14.2. Коэффициент линейной корреляции и его свойства
- •14.3. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции
- •14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов
- •14.5. Нелинейная регрессия
- •14.6. Варианты заданий
- •Приложение
- •Критические значения выборочного коэффициента корреляции
- •Критерий Колмогорова – Смирнова Точные и асимптотические границы для верхней грани модуля разности истинной и эмпирической функции распределения
- •Распределение Пирсона (х2 – распределение)
- •Распределение Фишера – Снедекора (f-распределение)
- •Библиографический список
- •Содержание
- •Глава 13. Статистический анализ результатов исследований 150
- •Глава 14. Корреляционный и регрессионный анализ 168
9.5. Примеры
№1.
Найти приближенное значение определенного
интеграла
![]() с помощью формулы Симпсона и формулы
трапеций, разбив отрезок интегрирования
на 10 частей.
с помощью формулы Симпсона и формулы
трапеций, разбив отрезок интегрирования
на 10 частей.
Решение.
Так как п=2т, то в нашем примере т=5. По формуле Симпсона получим:

Все дальнейшие расчеты приведены в таблице:
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
xi |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y(xi) |
2,83 |
3,87 |
4 |
4,12 |
4,9 |
6,56 |
8,94 |
11,87 |
15,23 |
18,95 |
22,98 |
Окончательно получим,

Точное значение этого интеграла – 91.173.
Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная.
Абсолютная
погрешность равна
![]() .
.
Относительная
погрешность
![]()
Для сравнения применим к этому же интегралу формулу трапеций.

Абсолютная
погрешность равна
![]() .
.
Относительная
погрешность
![]()
Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.
№2.
Вычислить определенный интеграл
![]() с помощью формулы прямоугольников,
еслип=10.
с помощью формулы прямоугольников,
еслип=10.
Решение.
По
формуле прямоугольников получим:
![]() .
.
Резльтаты вычислений поместим в таблицу:
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
ti |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
y(ti) |
1 |
0,99 |
0,96 |
0,92 |
0,86 |
0,80 |
0,74 |
0,67 |
0,61 |
0,55 |
Таким образом,
![]() .Точное
значение этого интеграла – 0,79.
.Точное
значение этого интеграла – 0,79.
Найдем точное значение интеграла

Абсолютная
погрешность равна
![]() .
.
Относительная
погрешность
![]()
Вывод: формула прямоугольников для данного числа разбиений дала достаточно точный результат (погрешность меньше 1%).
№3.
Найти площадь
криволинейной трапеции, ограниченной
графиком функции y
=
![]() и прямыми:y
= 0, x
= a
= 1, x
= b
=11 методами:
и прямыми:y
= 0, x
= a
= 1, x
= b
=11 методами:
а) прямоугольников;
б) трапеций;
в) Симпсона;
г) аналитическим с использованием формулы Ньютона-Лейбница.
Построить
график заданной функции с разбиением
отрезка
![]() наn
= 10 подынтервалов и график функции
наn
= 10 подынтервалов и график функции
![]() на
отрезкеx
на
отрезкеx![]()
![]() .
.
Решение.
Составим таблицу разбиения отрезка
интегрирования на n
= 10 равных участков с длинами интервалов
x
=![]() (табл. 11.1). Во второй строке таблицы
представлены увеличенные в 10 раз
значения
(табл. 11.1). Во второй строке таблицы
представлены увеличенные в 10 раз
значения![]() (k
=
(k
=
![]() ).
).
Таблица 9.1 Данные для численных методов
|
|
1 2 3 4 5 6 7 8 9 10 11 |
|
|
10 7,07 5,77 5,00 4,47 4,08 3,78 3,54 3,33 3,16 3,02 |
а) Используя формулу прямоугольников с высотами, представляющими собой левые значения функции на концах подынтервалов, найдем приближенное значение площади криволинейной трапеции в виде суммы площадей прямоугольников, очерченных на рис. 11.6 сплошными линиями:
![]() Та
же формула прямоугольников, но с
подстановкой в нее высот, равных правым
значениям функции на концах подынтервалов,
дает значение интеграла, равного площади
ограниченных пунктиром прямоугольников:
Та
же формула прямоугольников, но с
подстановкой в нее высот, равных правым
значениям функции на концах подынтервалов,
дает значение интеграла, равного площади
ограниченных пунктиром прямоугольников:
![]()
б) По формуле трапеции получим

Следует обратить внимание на очевидное равенство
![]()
в) По формуле Симпсона (n=5–количество спаренных подынтервалов)

г) Определим точное значение интеграла, являющегося табличным:
![]()
Найдем относительные ошибки определения площадей различными использованными методами численного интегрирования, сравнивая их с точным значением площади, полученным по формулам Ньютона-Лейбница:

Аналогично:
![]()
![]() ;
;