8.5.2. Примеры решения задач.

№1. В условиях неограниченных ресурсов питания скорость (t)=роста многих популяций экспоненциальна, т. е.(t)=ae^kt. Найти прирост n популяции за время t=t₂-t₁.

Решение: Так как =, тоdn= (t)dt, откуда n=(t)dt или n=n(t₂)-n(t₁)=n(t)

№2. Расстояние пружины x пропорционально приложенной силе –F (закон Гука): F=kx. Вычислить работу силы F при растяжении пружины на 5 см ( 0,05м), если k=200 (Н/м).

Решение: На основании формулы работы имеем:

№3. 100 г. двуокиси углерода нагревается при постоянном объёме от 105 до 1000 С. Определить количество поглощаемой при этом теплоты, если теплоёмкость сv=A(B+Dt) Дж/моль*град, где A=4,19; B=6,5; D=0,00193.

Решение. Количество теплоты, поглощаемой при повышении температуры от t₁ до t₂, для одного моля выражается формулой

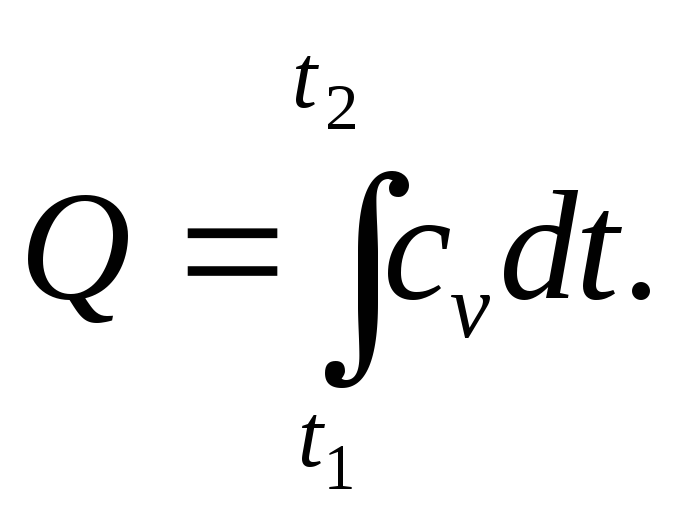
В нашей задаче число молей CO₂ равно 100/44.

Q=

№4. Найти энергию связи между ионами в отдельной молекуле хлорида калия (KCl), если постоянная решетки KCl r=2,79(1=10^-8см) и связь между атомами в молекуле KCl электростатическая. Заряд иона e=4,803*10^-10 ед. CGSE.

Решение. Энергия связи равна работе по перемещению иона из бесконечности до расстояния, равного постоянной решетки. Сила взаимодействия между ионами подчиняется закону Кулона и для любого расстояния x равна F(x)=e²/x². Энергия связи

E=A=эрг.

8.5.3. Варианты заданий

1) При прохождении электрического тока по нервному волокну оно возбуждает при условии, что проходящий ток больше рогового. Предполагается, что возбуждающий ток увеличивает величину параметра состояния , называемого «электрическим возбуждением». Как только  превышает определенное значение _0, возникает возбуждение. Скорость изменения  зависит от тока i:

.

Определить связь между параметром  и i при условии, что на нервную ткань воздействуют с постоянным током.

2) Найти путь S, пройденный материальной точкой от начала движения (t=0) до её остановки, зная скорость V(t) её прямолинейного движения: V(t)= 18t - 6t² (м/с).

3) Два электрических заряда q₁=1 Кл и q₂=1,2 Кл находятся в воздухе (=1) на расстоянии x₁= 0,2 м. Какую работу надо затратить, чтобы сблизить заряды до расстояния x₂=0,05 м.

4) Получит общее выражение для работы, совершенной молями идеального газа при изотермическом расширении отV₁ до V₂.

5) Скорость изменения в крови концентрации C препарата с изотопным индикатором зависит от времени q ни t (час) по закону:

а) б)

Найти концентрацию препарата в крови через t=4 часа, если начальная концентрация .

6) Вычислить работу переменного тока J=J₀sin t за период T (за время t₁=0 до t₂ =T) при прохождении его через проводник с сопротивлением R (- круговая частота, 

7) Воздух содержит a=8% CO₂; он пропускается через цилиндрический сосуд с поглотительной массой. Тонкий слой массы поглощает количество газа, пропорциональное его концентрации и толщине слоя.

а) Если воздух, прошедший слой в H = 10 см толщиной, содержит b=2% CO₂, то какой толщины должен быть поглотительный слой, для того чтобы, выходя из поглотителя, воздух содержался C = 1% CO₂ углекислоты?

б) Сколько углекислоты (d%) останется в воздухе, прошедшем поглотитель, если толщина поглотительного слоя будет равна 30 см?

8) Если при прохождении через слой воды толщиной x₁ =3м поглощается половина первоначального количества света, то какая часть этого количества дойдёт до глубины x₂ = 30 м. (Количество света dJ, поглощенного тонким слоем воды, пропорционально толщине dx слоя и количеству света J, падающего на поверхность его - dJJdx ).

9) Если первоначальное количество фермента 1 г через час становится равным 1,2 г, то чему оно будет равно через 5 часов после начала брожения, если считать, что скорость прироста фермента пропорциональна его начальному количеству?

10) Найти функцию, производная от которой равна sinx +2cosx и при x= принимает значение, равное 4.

11) Найти уравнение кривой, проходящей через точку А(2; 1), зная, что наклон касательной к кривой в каждой её точке равен x.

12) Найти функцию обращающуюся в 2e при x=1, если производная от этой функции равна .

13) Скорость тела задана формулой =(6t²+2t)м/с. Найти уравнение пути s, если за t = 3 с тело прошло путь s=60 м.

14) Скорость точки задана уравнением =(t²-2t+5)м/с. Найти уравнение движения точки, если в начальный момент времени она находится в начале координат.

15) Скорость движущейся точки дана уравнением  = 2e^t м/с. В момент t = 1 с точка находится на расстоянии s = 3e м от начала отсчета. Найти закон движения точки.

16) Тело, брошенное вертикально вверх, имело начальную скорость ₀=73,5 м/с. Пренебрегая сопротивлением воздуха, найти, через сколько секунд оно достигнет наибольшей высоты.

17) 100 г. двуокиси углерода нагревается при постоянном объёме от 105^ до 900^ С. Определить количество поглощаемой при этом теплоты, если теплоёмкость с_v=A(B+Dt) Дж/моль*град. где A=4,24; B=7,5; D=0,00215.

18) Скорость движения тела выражена формулой v=(3t²-2t) м/с. Какой путь пройдёт тело за 5 с от начала движения?

19) Найти работу, произведённую при сжатии пружины на 3 см, если известно что сжатия её 0,5 см нужно приложить силу в 10 Н.

20) В цилиндре с подвижным поршнем заключен атмосферный воздух. Объём цилиндра равен 0,2 м³. Поршнем воздух сжимается до объёма 0,06 м³. Найти работу, произведенную силой давления воздуха, если температура воздуха поддерживается постоянной.

21) Тело движется в некоторой среде прямолинейно по закону s=t². Сопротивление среды пропорционально квадрату скорости движения. Найти работу, произведенную силой сопротивления среды, при передвижении тела от s=0 до s=a.

22) Вычислить работу, затрачиваемую спортсменом при растяжении пружины эспандера на 70 см, если известно, что при усилии в 10 Н эспандер растягивается на 1 см.

23) Два электрических заряда: q₁=100 ед. CGSE и q₂=120 ед. CGSE находятся в воздухе на расстоянии 20 см друг от друга. Каким будет расстояние между зарядами, если приблизить второй к первому, затратив при этом работу в 1800 эрг?

24) Вычислить работу тока за время от t₁=0 до t₂=T, если сила тока определяется формулой I=I₀ sin w₀t, где I₀- максимальное значение тока; w₀- круговая частота; t- время.

25) Формула температурной зависимости истинной мольной теплоёмкости Fe₂O₃:

c_= A (B+CT-DT²) кал/моль*град.

Где A=4,19; B=24,72; C=16,04; D=4,234. Определить количество теплоты (в кДж), необходимое для нагревания 1 кг Fe₂O₃ от 16 до 1538 С.

26) На расстоянии xнаходятся два тела массами m₁ и m₂, которые взаимодействуют друг с другом с силой F=y. Вычислить работу, которую производит эта сила при перемещении тела m₂ в бесконечность из положения x=a.

27) Найти среднее значение электродвижущей силы E_ср, изменяющейся со временем по закону E=E₀sint, и среднее значение её квадрата E²_ср в течение одного полупериода, т. е. от t=0 до t=T/2.

28) Найти массу стержня длинной 0,50 см, если линейная плотность стержня меняется по закону =(5x+0,4x²) кг/м, где x – расстояние от одного из концов стержня.

29) Найти количество тепла, выделяемое переменным синусоидальным током I=2sinв течение периода T=0,02 с в проводнике с сопротивлением 100 Ом.

30) Некоторая масса газа при давлении 10⁴ Н/м² занимает объём 4 м³. Какую работу надо совершить над газом, чтобы, не изменяя его температуры, уменьшить объём до 1 м³?

8.6. Контрольные вопросы

1. Дайте понятие интегральной суммы.

2. Что называется определенным интегралом?

3. Запишите формулу Ньютона-Лейбница.

4. Перечислите основные свойства определенного интеграла. Сформулируйте теорему о среднем.

5. Каковы характерные особенности применения метода замены переменной к вычислению определенного интеграла?

6. Каковы характерные особенности применения метода интегрирования по частям к вычислению определенного интеграла?

7. В чем состоит геометрический смысл определенного интеграла?

8. Приведите примеры применения интегрального исчисления в биологии и медицине.