
Все в одном
.pdf
1. ДИСКРЕТНАЯ МАТЕМАТИКА
1. Элементарные понятия
Опр: Высказывание A – связное повествовательное осмысленное предложение, о котором можно сказать, истинно оно или ложно. Высказывания должны быть связными, т.е. построенными по законам языка. Нас интересуют только значения
истинности ˆ высказывания.
A
Два высказывания А и В называют равносильными (А≡В) тогда и только тогда, когда
ˆ |
ˆ |
|
|
|
|
|
|
A = B . |
|
|
|
|
|
|
|
Операции: |
|
|
|
|
|
|
|
|
операнды |
отрицание |
дизъюнкция |
конъюнкция |
|
эквиваленция |
импликация |
|
( aˆ или |
|
|||||
|
ˆ |
^ |
^ |
|
^ |
^ |
|
|
ˆ |
a b |
a b |
|
a ~ b |
a b |
|
|
a |
|
|||||
|
aˆ , b ) |
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
0,0 |
|
0 |
0 |
|
1 |
1 |
|
0,1 |
|
1 |
0 |
|
0 |
1 |
|
1,0 |
|
1 |
0 |
|
0 |
0 |
|
1,1 |
|
1 |
1 |
|
1 |
1 |
Свойства импликации и эквиваленции: 1) a ~ b b ~ a ; |
2) a ~ a 1; |
|
|||||
3)a b a b , где а-посылка, b-заключение;
4)a ~ b (a b) (b a) (a b) (a b) (a b) (a b) .
Опр: ФАВ – осмысленное выражение, полученное из элементарных высказываний, символов логических переменных, с помощью знаков логических операций и скобок, определяющих порядок действий.
Опр: Булевой формулой алгебры высказываний (далее БФАВ) называется формула алгебры высказываний (далее ФАВ), не содержащая Опр: Булева алгебра высказываний (БАВ) – некоторое множество объектов с тремя
операциями: , , , если в нем справедливы 19 соотношений:
Основные равносильности булевой алгебры высказываний (БАВ)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
a a |
закон _ двойн ого_ отрицан ия |
|||||||||
1 |
|
a b b a |
коммутативн ый _ закон |
||||||||||
2 |
|
a b b a |
коммутативн ый _ закон |
||||||||||
3 |
(a b) c a (b c) a b c |
ассоциативн ый _ закон |
|||||||||||
4 |
(a b) c a (b c) a b c |
ассоциативн ый _ закон |
|||||||||||
5 |
a bc (a b)(a c) |
дистрибутивн ый _ закон |
|||||||||||
6 |
a(b c) ab ac |
дистрибутивн ый _ закон |
|||||||||||
7 |
|
a a a |
закон _ идемпотен тн ости |
||||||||||
8 |
|
a a a |
закон _ идемпотен тн ости |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
9 |
|
a b a b |
закон _ Де _ Морган а |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
10 |
|
a b a b |
закон _ Де _ Морган а |
||||||||||
11 |
|
a 1 1 |
закон _ н уля _ и _ един ицы |
||||||||||
12 |
|
a 0 0 |
закон _ н уля _ и _ един ицы |
||||||||||
13 |
|
a 0 a |
закон _ н уля _ и _ един ицы |
||||||||||
14 |
|
a 1 a |
закон _ н уля _ и _ един ицы |
||||||||||
15 |
|
a ab a |
закон _ поглощен ия |
||||||||||
16 |
|
a(a b) a |
закон _ поглощен ия |
||||||||||
|
|
|
|
|
|
|
|||||||
17 |
|
a a 1 |
закон _ исключен н ого _ третьего |
||||||||||
|
|
|
|
|
|
||||||||
18 |
|
a a 0 |
закон _ противоречивости |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Пусть F (x1 |
... xn ) - ФАВ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
def |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Опр: Двойственной формулой называется F * (x1... |
xn ) F (x1... |
xn ) . |
||||||||||||||||||
Теорема: Общий принцип двойственности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пусть F ( y1... ym ), f1 (x1...xn ),..., |
f m (x1...xn ) - ФАВ => |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Fyi fi |
(x1 ... |
x n ) * F *yi f *i |
(x1 |
...xn ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
▲ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fyi fi |
(x1 |
x n ) * F( f1 (x1 |
xn ),...,fm (x1 xn )) * |
|
|
|
|
|
|
|
|
|
|
|
||||||
F( f1 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x1... |
xn ),...,fm (x1... |
|
xn )) |
|||||||||||||||||
F( f1 (x1...xn ),..., fm (x1...xn )) F *yi f *i (x1...xn )
Теорема: (Булев принцип двойственности):
Двойственная БФ м.б. получена заменой 0 на 1, 1 на 0, на , на с сохранением структуры формулы.
▲Параметр индукции – ранг формулы r(f) (кол-во операций в формуле).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
При r=0 0,1, x |
|
0* 0 1,1* 1 0, x* x x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2. |
При r=1 формула состоит из булевых формул f,g и операций , , . Тогда |
|||||||||||||||||||||||||||||||
|
|
|
|
|
общ.принцип |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
двойст ти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
( f )* ( y y f ) * |
|
|
|
( y) *y f * ( y) y f * ( f *) , |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
общ.принцип |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
двойст ти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
( f g)* ( y y |
y1 f |
) * |
|
|
( y y |
|
) * |
|
|
|
|
( y y |
|
) |
|
( f ) * (g) * |
|||||||||||||||
|
1 |
|
2 y2 g |
|
|
|
|
|
|
|
1 |
|
2 |
|
y1 f * |
|
|
1 |
2 |
|
y1 f * |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 g* |
|
|
|
|
|
y2 g* |
|
|
|
|||
|
|
|
|
|
|
|
общ.принцип |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
двойст ти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
( fg)* ( y y y1 f |
) * |
|
|
|
( y y |
) * |
|
|
|
( y y |
) |
|
|
|
( f ) * (g) * |
||||||||||||||||
|
|
|
|
|
1 2 y2 g |
|
|
|
|
|
|
1 2 |
|
y1 |
f * |
|
1 |
|
2 |
|
y1 f * |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 g* |
|
|
|
|
|
|
|
y2 g* |
|
|
|
|
||||
Индуктивный переход: пусть формула справедлива при r n0 , покажем при r n0 1 : в любой формуле можно выделить последнюю операцию, это одна из трёх , , . А к ней применимо то же, что и в п.1 для r=1, т.е. ( f )* ( f *) , ( f g)* ( f ) * (g) *и
( fg)* ( f ) * (g) * .
Теорема: (Закон двойственности) f g f * g *
▲ Основано на анализе связей таблиц истинности формулы и её двойственной
def |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формулы. Т.к. F * (x1...xn ) F (x1...xn ) , то |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
… |
xn |
ˆ |
ˆ |
|||||
|
|
|
|
|
|
f |
f * |
|||||||||
|
|
|
|
0 |
|
0 |
… |
0 |
|
|
|
|
|
|
||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
… |
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
… |
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
1 |
… |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||||||||
ˆ |
^ ^ |
ˆ |
|
f g f |
g f * g * f * g * |
обобщ
f * g * ( f *)* (g*)* f g

|
|
|
|
||
Пусть {0,1}, х – высказывательная переменная. |
x |
|
x |
, |
if 0; |
|
if 1. |
||||
|
|
x, |
|||
Ур-ие x 1, где х-неизв., -парам-р, имеет един-ое реш-ие x .
Лемма (о дизъюнктивном разложении по переменной): Пусть f (x1,..., xn ) -ФАВ, 1 i n
=>
f (x1 ,..., xn ) xi f (x1 ,..., xi 1 ,1, xi 1 ,..., xn ) xi f (x1 ,..., xi 1 ,0, xi 1 ,..., xn )xi i f (x1 ,..., xi 1 , i , xi 1 ,..., xn )
i {0,1}
▲Разобьем множество значений всех переменных на 2 подмножества:
I – такие наборы, в которых xi=1; II – такие наборы, в которых xi=0;
I.Левая часть: f (x1 ,..., xn ) f (x1 ,..., xi 1 ,1, xi 1 ,..., xn )
Правая часть:
11 f (x ,..., x |
i 1 |
,1, x |
i 1 |
,..., x |
n |
) 10 f (x ,..., x |
i 1 |
,0, x |
i 1 |
,..., x |
n |
) f (x ,..., x |
i 1 |
,1, x |
i 1 |
,..., x |
n |
) |
1 |
|
|
1 |
|
|
1 |
|
|
|
Левая = Правая.
II.Левая часть: f (x1 ,..., xn ) f (x1 ,..., xi 1 ,0, xi 1 ,..., xn )
Правая часть:
|
|
|
|
|
|
|
01 f (x ,..., x |
i 1 |
,1, x |
i 1 |
,..., x |
n |
) 00 |
f (x ,..., x |
i 1 |
,0, x |
i 1 |
,..., x |
n |
) |
f (x ,..., x |
i 1 |
,0, x |
i 1 |
,..., x |
n |
) |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
Левая = Правая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим произвольную ФАВ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
f (x ,...,x |
|
) |
|
x n |
f (x ,...,x |
|
|
, |
|
) |
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
n 1 f (x ,..., |
|
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
n |
n 1 |
n |
|
n |
|
|
|
|
|
|
n 1 |
n |
) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
n |
|
1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n 1 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n {0,1} |
|
|
|
|
n 1 {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
n |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
рекурсивно |
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
xn 1 |
f (x1 ,..., n 1 , n ) |
|
|
|
|
|
|
|
|
|
|
|
|
f ( 1 |
,..., n ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
xn |
|
|
|
|
|
|
x1 |
|
...xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
n {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ... n {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
n |
1 {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( 1 ,..., n ) - это уже высказывание. Отбросим слагаемые, для которых |
|
f ( |
|
^ |
n ) 0 |
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 ,..., |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
получим СДНФ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Опр: СДНФ – это |
f (x ,..., |
|
x |
n |
) |
|
|
|
|
|
|
|
x |
1 ...x |
n |
|
при условии, что |
f (x ,..., x |
n |
) 0 . |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ... n^ {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( 1 ,..., n ) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Булев_ принцип |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 1 ...xn n ) * |
двойственности |
|
|
|
(x1 1 ... xn n ) |
|
||||||||||||||||||||||||
f (x1 ,...,xn ) ( f *)* (СДНФ( f *))* ( |
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1... n {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
... n {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f *( 1 ,..., n ) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
( 1 ,..., n ) * 1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
i i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
& |
|
|
(x1 1 |
... xn n ) |
|
|
|
|
|
& |
|
|
(x1 |
1 ... xn n |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1... n {0,1} |
|
|
|
|
|
|
|
|
|
|
1 |
... n {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( |
1 |
,..., |
|
) |
|
0 |
|
|
|
|
|
|
|
|
|
f ( 1 ,..., n ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Опр: СКНФ – это |
|
|
|
|
|
|
|
|
|
при условии, что |
|
f (x1 ,..., |
xn ) 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||
f (x1,...,xn ) |
|
|
& (x1 |
1 |
... xn n ) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1... n {0,1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
^
f ( 1 ,..., n ) 0
Теорема: (Единственность СДНФ).
▲ Рассмотрим уравнение f (x1 ,..., xn ) 1. Так как f (x1 ,...,xn ) |
x1 1 ...xn n , то |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1... n |
|
|
|
|
|
f (x1 ,...,xn ) 1 |
|
|
|
1 |
|
n |
|
|
|
|
|
1 |
|
n |
1. - |
|
|
|
|
|
|
|
|
||||||||
|
|
x1 |
|
|
|
|
|
|
...xn |
||||||
1 ... n |
|
...xn |
1 и оно равносильно уравнению |
|
x1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
1... n |
|
|
|
|||
един-ое множество решений, т.е. наборов , для которых f ( 1 ,..., n ) 1. |
|
|
|
||||||||||||
Теорема: (Единственность СКНФ). |
|
|
|
|
|
|
|
|
|||||||
▲ Допустим противное: |
f |
СКНФ ( f ) |
двойств |
(СКНФ ( f ))* СДНФ ( f ) |
, что |
|
|
||||||||
СКНФ ( f ) |
|
f * (СКНФ ( f ))* СДНФ ( f ) |
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
противоречит единственности СДНФ.
def
Пусть x1…xn – высказывательные переменные. Vn {x1 , x1 ,..., xn , xn } . Рассмотрим v из Vn.
Опр: ЭК(v) – это конъюнкция некоторых элементов v. Опр: ЭД(v) – это дизъюнкция некоторых элементов v. Опр: ПЭД(v) – это полная ЭД(v), т.е. когда
{xi , xi } хотя бы что-то входит).
Опр: СЭД(v) – это совершенная ЭД(v), т.е. когда | v {xi , xi } | 1(т.е.в ЭД не входит ни какая переменная вместе со своим отрицанием).
Опр: ПСЭД(v) – это полная совершенная ЭД(v), т.е. содержит представления переменной.
Т.о., СКНФ &ПСЭД; |
СДНФ ПСЭК . |
Опр: ДНФ – формула, имеющая вид дизъюнкции элементарных конъюнкций (ЭК). Опр: КНФ – формула, имеющая вид конъюнкции элементарных дизъюнкций (ЭД).
Теорема: ФАВ эквивалентная (равносильная) ей ДНФ.
▲Приведем алгоритм:
1)Является ли формула константой?
0 xi xi Да: её ДНФ= 1 xi xi
xi xi
Нет: goto 2)
2)Перейти к булевой форме записи (убрать все ~, ).
3)По формулам Де Моргана опускать все отрицания, пока возможно.
4)По дистрибутивным законам сделать дизъюнкцию внешней операцией.
Теорема: ФАВ равносильная ей КНФ и СДНФ.
Критерий.
ЭК≡0 ЭК – несовершенна (т.е. в ней присутствует хоть одна пара (перем, перем) ). ▲ Если ЭК – несовершенна, то есть {xi , xi } v ЭК(v) x1...xi xi ...xn 0
ЭК≡0. Допустим, что она явл. СЭК(=0)=>в ней нет ни одной пары (перем, перем) .
1)элементы , их отриц-й нет
2)элементы , но нет самого эл-та
3)остальные (т.е. нет ничего)
Образуем набор знач-й переем-х ( 1… n), i=1 до n, по правилу:

|
|
|
|
i |
перем _ или3 |
|
|
|
|
|
|
|
||
|
|
1, если x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 0 |
0 ... 1-противоречие. |
|||||||||
Т.е. |
i |
|
|
|
|
|
|
Подставляем в ЭК: 1 |
||||||
0,если |
|
xi перем |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Критерий:
ЭД≡1 ЭД – несовершенна (т.е. в ней присутствует хоть одна пара (перем, перем) ).
Критерий(тожд-й ложности): ФАВ≡0 ДНФ(ФАВ)≡0 ЭК≡0
Критерий: ФАВ≡1 КНФ(ФАВ)≡1 ЭД≡1
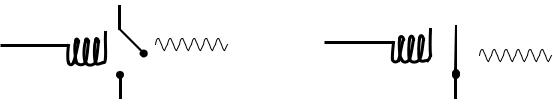
2. Релейно-контактные схемы
{Наличие тока – 1, Отсутствие тока – 0} – управляющие сигналы.
Нормально-разомкнутое реле (ННР) |
Нормально-замкнутое реле (НЗР) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Управ-й сигнал |
Ф-я.провод-ти НРР |
Ф-я.провод-ти НЗР |
0 |
0 |
1 |
1 |
1 |
0 |
Задачи теории РКС:
1)задача анализа схемы (нахождение функции проводимости по схеме)
2)задача синтеза (построить схему проводимости для 01-функции)
3)задача упрощения схемы
Анализ не всегда удается.
Опр: РКС – устройство, представляющее собой электрическую схему с элементами – реле, входами – управляющими обмотками и выходами – свободными выводами РКгрупп реле.
|
|
схема |
|
функция |
||||||||||
|
|
|
проводимости |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f pr x y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
y |
|
f pr x y |
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема:
Задача синтеза всегда разрешима.
▲ f(01)-функция может быть представлена в виде ФАВ. ФАВ м.б. преобразована к
булевой ФАВ с «тесными» отрицаниями, а по такой ФАВ можно строить схему. Задача упрощения: по РКС записывается fпр, её преобразуем к СДНФ или СКНФ.
Машина голосования: Комитет из 3 человек голосует. Выигрывает большинство голосов. Построить устройство, автоматизирующее процесс.
Решение:
x |
y |
z |
ˆ |
f pr |
|||
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1

1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
-таблица зависимости решения |
ˆ |
от голосов x,y,z. Строим СДНФ: |
||||||||||||||||||||||||||||
f pr |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
идемпотентность |
|
|
|
|
|
|
|
|||
СДНФ xyz x yz xy z xyz |
|
|
|
xyz xyz x yz xyz xy z |
xyz |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
исключенное 3 |
|
||||||||
yz(x x) xz( y y) xy(z z) |
|
|
|
yz xz xy yz x(z y) |
|
|||||||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
x |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
x |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
y |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Одноразрядный двоичный сумматор:
xi, yi – значение слагаемых в i-м разряде, pi – перенос в i-й разряд, zi – результат суммирования в i-м разряде.
xi |
yi |
pi |
zi |
pi+1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
pi 1 xi yi pi zi xi yi pi zi xi yi pi zi xi yi pi zi xi yi yi pi xi pi zi pi 1 (xi yi pi ) xi yi pi
2
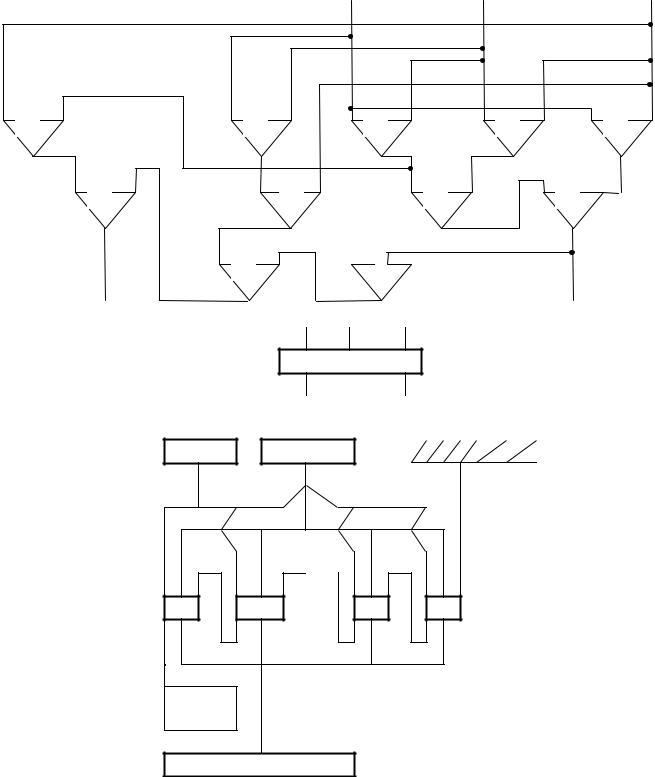
xi |
yi |
pi |
Λ |
V |
Λ |
Λ |
Λ |
V |
V |
V |
V |
Λ |
Ø |
zi |
pi+ |
Если обозначить этот блок через
xi yi pi
∑i
zi |
pi+1 |
, то можно организовать n-разрядный 01 сумматор:
X + Y
земля
|
|
… |
|
z |
z |
|
z |
|
|
… |
|
∑n |
∑n-1 |
∑2 |
∑1 |
На УУ компа
X+Y
, где z – элемент задержки (синхронизатор).
3
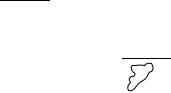
3. Отношения.
Пусть x1…xn – непустые множества.
Опр: N-местным отношением, заданным на декартовом произведении x1 ... xn называется S x1 ... xn .
Опр: Точка (x1…xn) связана отношением S, если (x1 ,..., xn ) S .
Пусть n=2.
Опр: Двуместное отношение - это (x1 , x2 ) S x1 s x2 .
Опр: Бинарное отношение на Х – это двуместное отношение на X X .
композиции 2х отношений.
Пусть бин-е отн-е определено на декартовом кв-те Х×Х.
Свойства бинарных отношений
1.Рефлексивно, если xÎХ (x x)≡1
2.Симметрично, если xÎХ yÎХ ((x y)~(y x))≡1
3.Транзитивно, если xÎХ yÎХ zÎХ ((x y)&(y z)(x z))≡1
4.Антисимметрично, если xÎХ yÎХ ((x y)&(y x)(x=y))≡1
Опр: Бинарное отношение – отношение порядка, если оно рефлексивно, транзитивно и антисимметрично. Пример: «<» Опр: Бинарное отношение на множ-ве Х – отношение эквивалентности, если оно
рефлексивно, транзитивно и симметрично. Пример: «=» Опр: Пусть - отношение эквивалентности на
эквивалентности эл-та х - множество такое, что y X |
|
x y . |
|
||
|
|
|
Примеры:
1)X , " ", x X [x] x
2)X C, равенство _ модулей _ компл _ чисел,[i] {z C,| z | 1}
3)X C, равенство_ аргументов_ компл_ чисел,[i] {z C, arg(z) 2}
4)X C, компл _ аргумент,[i] {z C, Re( z) 0}
|
|
1 |
0 |
|
|
5) X M |
2 2 (R), след, |
|
{матрицы_ у _ которых_ trace 2} |
||
|
|
|
|
|
|
|
|
0 |
1 |
|
|
Теорема: (Свойства классов эквивалентности) |
|||||
- отношение эквивалентности на Х => |
|
||||
1) |
[x] x X |
|
|
|
|
2) |
x y |
([ x] [ y] |
[x] |
[ y] ) |
|
3) [x] X
x X
▲1) Очевидно, т.к. - отношение эквивалентности => - рефлексивно =>
x X (x x) 1 x [x]
2)Пусть [x] [ y] . Зафиксируем элемент z [x] [ y] . Рассмотрим t [ y] .
Ясно, что z [x] [ y] |
z [x] z [ y] . Тогда выполнены: |
1

x z, т.к. z [x]
y z, т.к. z [ y] |
симметричн |
z y |
|
||
y t, т.к. t [ y] |
|
|
Из a. и b. =>
Из b. и c. =>
транз
(x y) & (z y) x y
транз
(x y) & ( y t) x t
Таким образом, t [x] [ y]
3)X {x} [x] X ,
x X x X
[x] |
и |
[x] |
|
[ y] |
|||
|
|
X X
x X
[ y] [ y] [x] |
|
[x] [ y] |
|
||
[x] [x] [ y] |
|
|
|
|
[x] X
Опр: Фактор-множество множества Х по отношению эквивалентности называется множество Х/ , элементами которого являются классы эквивалентности.
Примеры:
1)Х, “=”, => Х/= - множество всех одноэлементных подмножеств множества Х
2)С, , z1z2 <=> |z1|=|z2| => C/ - множество всех концентрических окружностей с центром в (0,0)
3)С, β, z1βz2 <=> arg(z1)=arg(z2) => C/β – множество лучей из начала координат.
4)С, γ, z1γz2 <=> Re(z1)=Re(z2) => C/γ – множество линий, параллельных оси i. 
2
