§9 Типовые звенья линейных систем и их динамические характеристики

Типовым элементарным динамическим звеном называется звено, динамика которого описывается диффернциальным уравнением не выше второго порядка.

Типовые звенья классифицируются в зависимости от вида дифференциального уравнения на позиционные, интегрирующие, дифференцирующие, запаздывания.

Позиционными называются звенья в левой части дифференциального уравнения которых выходная величина и её производные, а в правой – входная величина.

§9.1 Позиционные звенья

1)Усилительное звено:

уравнение звена имеет вид у(t)=kx(t) (1)

передаточная функция звена: W(p)=y(p)/x(p)=k;

переходная функция: h(t)=L^-1{W(p)/p}=L^-1{k/p}=k∙1(t).

Весовая функция представляет собой импульс, площадь которого равна к, т.е. при x(t)=δ(t); y(t)=ω(t)=k∙ δ(t)

Получим частотные характеристики усилительного звена.КЧХ:

W(jω)=k

AЧХ : А(ω)=к ; ФЧХ: φ(ω)=0 на всех частотах.

Рис 9.1 Динамические и частотные характеристики усилительного звена

2) Апериодическое звено I-го порядка

Звено, в котором при скачкообразном изменении входной величины выходная величина апериодически (по экспоненте) стремится к новому установившемуся значению, называется апериодическим (инерционным).

Пример (рис. 9.2):

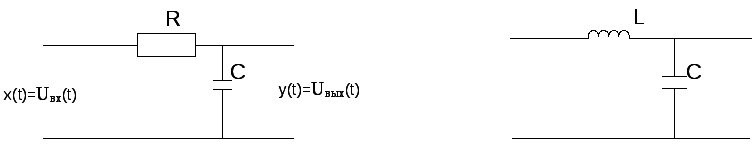
Рис. 9.2. Примеры инерционных звеньев

Дифференциальное уравнение звена имеет вид:

(1)

где Т – постоянная времени [c],

k – коэффициент передачи.

Операторное уравнение звена:

Тогда передаточная функция звена:

.

Переходная функция звена:

Весовая функция звена:

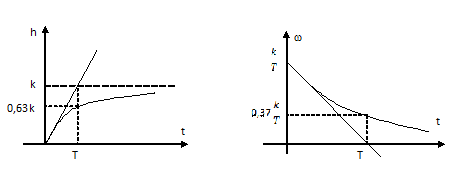
Рис 9.3 Временные характеристики инерционного звена

Постоянная времени Т представляет собой интервал времени, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости её изменения в начальный момент времени после поступления на вход единичного входного сигнала.

Чем >Т тем медленнее переходный процесс. Теоретически, переходный процесс в апериодическом звене длится бесконечно долго.

Под временем переходного процесса понимают промежуток времени, по истечении которого входная величина достигнет 0,95 от установившегося значения.

При t=3T

, т.е .

При t=T

Т можно определить как время, за которое входная величина изменяясь от 0 достигла 0,63 от установившегося значения, при подаче на вход звена единичного ступенчатого воздействия.

Для весовой функции при t=T:

.

Получим частотные характеристики звена.

КЧХ:

- АЧХ

- ФЧХ

В §.8. определяли ВЧХ и МЧХ:

;

Построим асимптотическую ЛАХ звена:

(2)

Для построения уравнения асимптот рассмотрим следующие интервалы частот:

1. При малых частотах

ωT<<1 или ω<<(1/Т) ,1/Т – частота сопряжения. Пренебрегаем величиной в (2), тогда уравнение первой асимптоты имеет вид:

(0 дб/дек)

2. При частотах ω>>(1/Т) пренебрегаем 1 в (2), тогда получим уравнение второй асимптоты:

(-20 дб/дек)

Рис. 9.5. Асимптотическая ЛАХ звена

Если построить действительную ЛАХ по уравнению (2), то наибольшая погрешность будет на частоте . Определим ΔL(ω):

дБ.

3. Апериодическое звено 2-го порядка

Дифференциальное уравнение звена имеет вид:

Операторное уравнение:

Разложим левую часть на множители:

, где и Т₄>Т₃

Тогда передаточная функция звена:

(1)

Очевидно, что Т₃, Т₄ могут быть как вещественными, так и комплексными.

При ;,корни будут вещественными, звено апериодическим 2-го порядка.

При <0; Т₁<2Т₂, корни будут комплексными, звено колебательным.

При Т₁=0 корни будут мнимыми, звено консервативным.

Из выражения (1) следует, что апериодическое звено 2-го порядка эквивалентно двум апериодическим звеньям 1-го порядка, соединённым последовательно.

Переходная функция звена:

Рис. 9.6. Временные характеристики апериодического звена 2-го порядка

Получим частотные характеристики:

Построим асимптотическую ЛАХ звена:

, Т₄>Т₃

1. При ω<(1/Т₄)<(1/Т₃)

(0 дБ/дек);

2. При (1/Т₄)<ω<(1/Т₃)

(-20 дБ/дек);

3. При ω>(1/Т₃)>(1/Т₄)

(-40 дБ/дек).

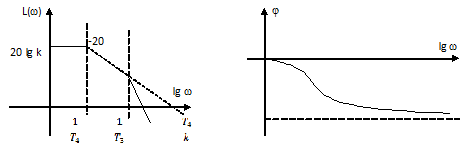
Рис. 9.7. Асимптотическая ЛАХ звена

4. Колебательное звено

Дифференциальное уравнение звена такое же как и у апериодического 2-го порядка:

.

Рис. 9.8. Примеры колебательных звеньев:

а) R,L,C – колебательный контур;б) механическая система ( m – масса;с – коэффициент упругости пружины;λ – коэффициент демфирования).

Характеристическое уравнение звена:

при <0 или Т₁<2Т₂. В этом случае отношение называютпостоянной затухания ( коэффициент демпфирования) колебательного звена.

При - колебательное звено; λ≥1 – апериодическое 2-го порядка; при λ=0 – консервативное.

Корни характеристического уравнения:

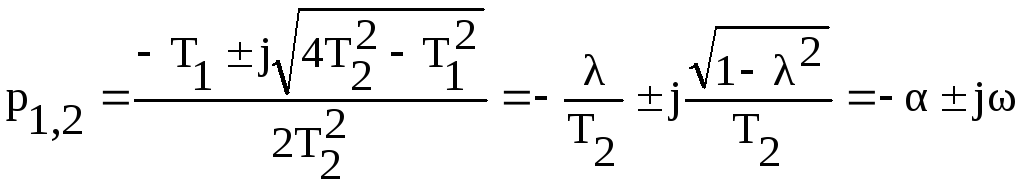
где -коэффициент затухания;

;

ω – частота собственных колебаний звена;

ω_с=1/Т₂ – угловая частота свободных колебаний при отсутствии затухания (λ=0).

Переходная функция колебательного звена:

(2)

Весовая функция:

(3)

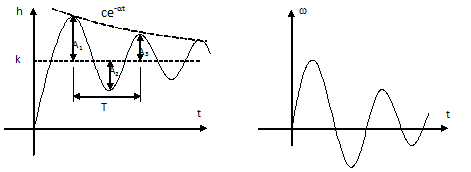
Рис. 9.9 Временные характеристики колебательного звена.

Уравнения (2), (3) характеризуют затухание во времени синусоидальных колебаний выходной величины с частотой .Затухание этих колебаний определяется величинойкоэффициента затухания α..

Из рисунка 9.9 следует, что чем меньше α, тем больше колебательность переходного процесса.

Колебательность можно оценивать по степени затухания Ψ, равной отношению разности двух соседних положительных амплитуд к большей из них (рис. 9.9):

,

Из рисунка 9.9 => => (4)

Чем ближе к единице Ψ, тем быстрее затухают колебания переходного процесса.

Получим частотные характеристики звена:

КЧХ:

При ;

Рис. 9.10 Частотные характеристики звена АЧХ, ФЧХ

Построим асимптотическую ЛАХ звена. - сопрягающая частота.

1) При (при ω→0) :

(0 дБ/дек);

2) При (при ω→∞):

(-40 дБ/дек).

Рис. 9.11 Асимптотическая ЛАХ колебательного звена.