§2 Математический аппарат исследования линейных систем автоматического регулирования

В §1 были рассмотрены основные функции элементов и систем автоматики, последовательность их включения в измерительную цепь.

При изучении динамических характеристик САР каждый элемент системы рассматривается только с точки зрения динамики его работы, вне зависимости от функционального назначения.

Структурной схемой САР называется схема, где элементы показаны в виде прямоугольников (блоков), а направление сигналов указывается стрелками. Внутри блоков пишутся операторы преобразования входного сигнала в выходной. Функциональное назначение элементов не определяется.

На рисунке 3.1 приведён пример структурной схемы системы стабилизации.

Рисунок 2.1 Структурная схема САР

Здесь Wp(р),Wo(р) - передаточные функции регулятора и объекта соответственно.

Динамика процессов управления, а также динамика работы элементов САР описывается дифференциальными уравнениями.

Линейной САР называется система, динамика работы которой описывается линейным дифференциальным уравнением.

Элементарным динамическим звеном называется часть САР, которая описывается дифференциальным уравнением не выше второго порядка.

Для упрощения решения дифференциальных уравнений используют преобразование Лапласа.

Преобразование Лапласа позволяет свести процесс решения линейного дифференциального уравнения к решению алгебраического уравнения при помощи специальных таблиц.

Таблица преобразований Лапласа

f(t)	F(p)
(t)	1
1(t)	1/p
	F(p+a)

При использовании преобразования Лапласа производится операция перехода от функций времени f(t) (оригиналов) к функциям F(p) (изображениям ) комплексной переменной р.

Символически это записывается следующим образом:

L {f(t)} = F(p) – прямое преобразование;

L {F(p)} = f(t) - обратное преобразование.

Свойства преобразования Лапласа:

1. L{f1(t)+f2(t)+….+fn(t)} = F1(p)+F2(p)+…+Fn(p)

2. L{A·f(t)} = A·F(p) , A=const

3. L{f(t – τ)} = e · F(p).

Теоремы Лапласа о начальном и конечном значениях функции:

Начальное значение функции:

f(0) = lim f(t) = lim p·F(p)

t→0 p→∞

Конечное (установившееся) значение функции:

f(∞) = lim f(t) = lim p·F(p)

t→∞ p→0

§ 3 Передаточные функции линейных звеньев

Рассмотрим динамическое звено, которое находится под воздействием полезного сигнала х(t) и возмущение f(t).

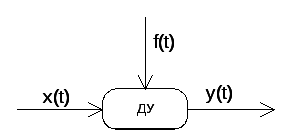
Рисунок 1 Динамическое звено

Тогда его динамика описывается линейным неоднородным дифференциальным уравнением вида:

(1)

преобразуем (1) по Лапласу при нулевых начальных условиях:

(2)

(3)

N(p), M(p), R(p) -операторные полиномы с постоянными коэффициентами;

Y(p),X(p),F(p)- изображение функций y(t),x(t),f(t) соответственно.

Передаточной функцией звена, по какому либо внешнему воздействию называется отношение изображения по Лапласу выходной величины к изображению по Лапласу рассматриваемого воздействия, при этом все другие внешние воздействия полагаются равными нулю.

Из определения следует, что для любого звена с одной выходной величиной число передаточных функций равно числу внешних воздействий.

Тогда для рисунка1 передаточная функция звена по полезному сигналу, при F(p)=0:

= (4)

передаточная функция звена по возмущающему воздействию , при X(p)=0:

(5)

из уравнений (4) и (5) следует, что

(6)

Многочлен N(p),фигурирующий в знаменателе передаточных функций звена, называют характеристическим полином этого звена, а уравнение

называется характеристическим уравнением звена. Оно представляет собой алгебраическое уравнение n-й степени и имеет n корней, среди которых могут быть как вещественные, так и комплексно-сопряженные.

Корни характеристического полинома называют полюсами передаточной функции, корни многочлена стоящего в числителе передаточной функции – нулями этой передаточной функции

Если известны передаточные функции для звена на рисунке 1, то изображение выходной величины, согласно принципу суперпозиции:

или (7)

Соотношение (7) удобно представить в виде структурной схемы звена (рисунок 2).

Рисунок 2 Структурная схема звена

ПРИМЕР 1: Дифференциальное уравнение звена имеет вид:

(8)

Найти передаточные функции звена. Получить структурную схему.

РЕШЕНИЕ: По дифференциальному уравнению (8) составим операторное уравнение, используя преобразование по Лапласу и его свойства.

Полагая F(p)=0, найдем передаточную функцию звена по полезному сигналу.

Полагая X(p)=0, найдем передаточную функцию звена по возмущающему воздействию:

Структурная схема звена представлена на рисунке 2.

ПРИМЕР 2. Структурная схема звена имеет вид (рисунок. 2). Передаточные функции определяются по выражениям:

Найти дифференциальное уравнение звена.

РЕШЕНИЕ:

Операторное уравнение звена:

Применяя обратное преобразование Лапласа и его свойства, получим дифференциальное уравнение: