§11.2 Интегральный регулятор

Регулятор, реализующий И-закон регулирования называется интегральным (И-регулятор). У И-регулятора изменение выходной величины (перемещение регулирующего органа) пропорционально интегралу от отклонения регулируемой величины. Уравнение динамики И-регулятора имеет вид:

u(t)= или

,

где - постоянная времени интегрирования, являющаяся настроечным параметром И-регулятора.

Из уравнения динамики следует, что скорость перемещения регулирующего органа пропорциональна величине рассогласования ε(t). Регулирующий орган будет перемещаться до тех пор, пока рассогласование (ошибка регулирования) не станет равным нулю: (илиu=const) при ε(t)=0.

Для И-регулятора характерно то, что при постоянно действующем возмущении он возвращает регулируемую величину к заданному значению, а следовательно устраняет ошибку системы: =0.

В динамическом отношении И-регулятор представляет собой идеальное интегрирующее звено с передаточной функцией

Рассмотрим реализацию И-закона на примере одноёмкостного объекта с самовыравниванием (рисунок 11.3).

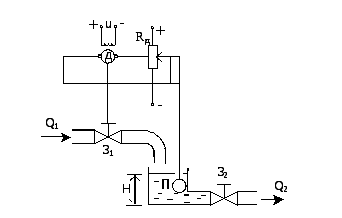
Рисунок 11.3 Пример реализации И-закона

В случае равенства уровень Н = Н(0), а поплавок П и задвижка З1 неподвижны. Движок потенциометрического датчиканаходится посередине, напряжение питания якоря равно нулю. При уменьшении расхода жидкости на величинууровень жидкости в баке начнет расти, поплавок поднимется и перемещает вверх движок датчика. В цепи якоря ДПТ появляется напряжениеU. Двигатель несколько закрывает задвижку З1 и приток жидкости Q1 уменьшается. В момент t1 величины Q1 и Q2 сравнялись (рисунок 11.3 б). Но так как уровень воды превышает заданный H(0), т.е. , интеграл от рассогласования будет возрастать и следовательно регулирующее воздействиеu(t) будет продолжать изменяться. В результате приток Q1 дополнительно уменьшится и станет меньше расхода Q2, поэтому уровень в баке начнет уменьшаться, что в свою очередь вызовет уменьшение расхода вытекающей жидкости Q2(t). В момент приток и расход жидкости сравняются и уровень достигнет заданного значенияH(0) (рисунок 11.3 в).

Процесс регулирования при И-законе прекратится, если одновременно будут выполнены 2 условия:

- уровень равен заданному H=H(0);

-приток жидкости равен расходу Q1=Q2.

Первое условие необходимо для того, чтобы регулирующее воздействие перестало изменяться. При выполнении второго условия в объекте достигается равновесие и уровень H постоянен. Эти условия выполняются, начиная с времени , которое определяет время регулирования.

Сравнительный анализ П и И регуляторов

И-регулятор при постоянно действующем возмущении возвращает регулируемую величину к заданному значению, то есть устраняется ошибка регулирования =0.(преимущество И-закона).

Однако при П-законе САР в переходном режиме будет иметь лучшие показатели качества, чем при И-законе регулирования (преимущество П-закона).

Рисунок 11.4 – Сравнение переходных характеристик П- и И-регуляторов.

В начальный момент времени П-регулятор сразу создает мощное регулирующее воздействие на объект. При И-законе, в начальный момент времени оно мало. Только спустя некоторое время воздействие И-регулятора достигает того же значения, что и при П-законе (рисунок 11.4).

Медленная реакция И-регулятора в начальный момент не позволяет достаточно эффективно компенсировать влияние возмущения на объект, поэтому в объекте при И- законе возникают более значительные динамические отклонения регулируемой величины, а сам процесс регулирования длится дольше.

Таким образом, П-регулирование обеспечивает хорошее свойство САР в переходном процессе, а И-регулирование позволяет полностью устранить ошибку регулирования.