3. Интервальное оценивание параметров

3.1. Необходимые понятия и функции распределения

В первой части практикума были кратко рассмотрены некоторые распределения, связанные с нормальным и играющие большую роль в математической статистике. Это распределения хи-квадрат, Стьюдента и Фишера.

Распределение хи-квадрат. Напомним, что если случайные величины ξ₁, …, ξ_n независимы и распределены нормально, т. е. ξ_j  N(0, 1)  j= 1, …, n, то  = ξ₁² +…+ ξ_n² χ_n², т.е. имеет хи-квадрат распределение с п степенями свободы, в свою очередь представляющее собой частный случай -распределения с параметрами масштаба b = 1/2 (или λ = 1/b = 2) и формы c = n/2; плотность распределения

(3.1)

(при x  0 f(x) = 0); математическое ожидание M = n, дисперсия D = 2n. При этом распределение хи-квадрат быстро сходится к нормальному (фактически, при n > 50), а величина () имеет приближённо стандартное нормальное распределение. Распределение хи-квадрат воспроизводит себя (безгранично делимо): если случайные величины ξ₁ и ξ₂ независимы и распределены по χ² (ξ₁  χ_n² и ξ₂  χ_m²), то случайная величина ξ = ξ₁ + ξ₂  χ²_n+m , то есть имеет хи-квадрат распределение с n + m степенями свободы.

Смысл понятия «степеней свободы» становится понятен из следующей леммы, лежащей также в основе многих статистических выводов.

Лемма Фишера. Пусть случайные величины ξ₁, …, ξ_n независимы и имеют стандартное нормальное распределение, т. е. ξ_j  N(0, 1)  j= 1, …, n, и (₁, ₂, …, _n)^T = A(ξ₁, ξ₂, …, ξ_n)^T, где А – ортогональная матрица (т.е. А^–1 = А^Т, «Т» – транспонирование). Тогда для любого r = 1, …, n – 1 справедливо 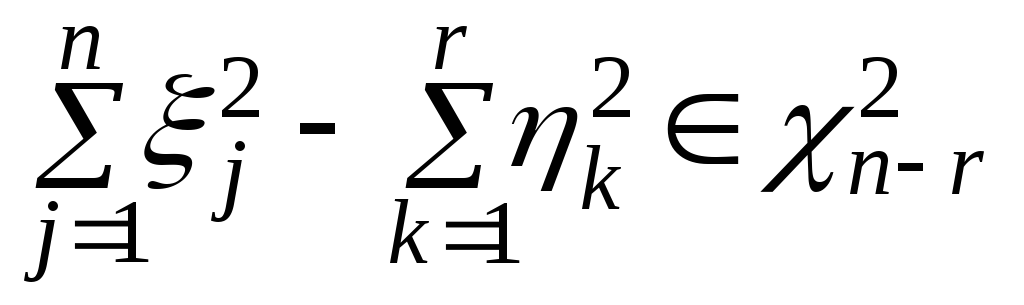и эта случайная величина не зависит от₁, …, _r.

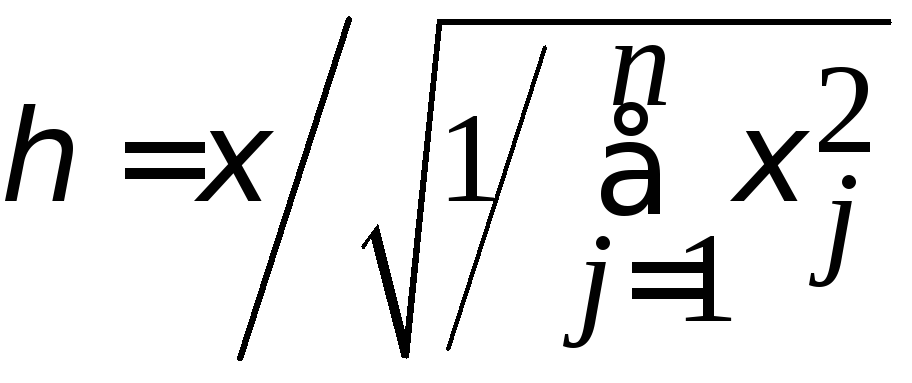
Распределение Стьюдента. Если случайные величины ξ, ξ₁, …, ξ_n независимы и все  N(0, 1), то случайная величина  Т_п , т.е. имеет распределение Стьюдента с п степенями свободы с функцией плотности распределения

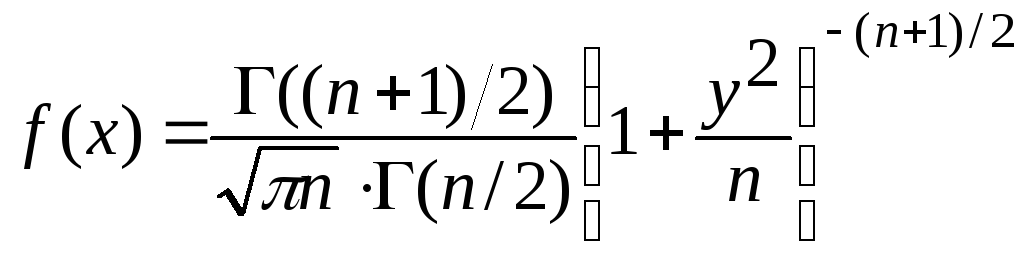. (3.2)

Математическое ожидание M = 0, дисперсия D = n/(n – 2) при n > 2, при n  2 D = . Распределение Стьюдента также безгранично делимо.

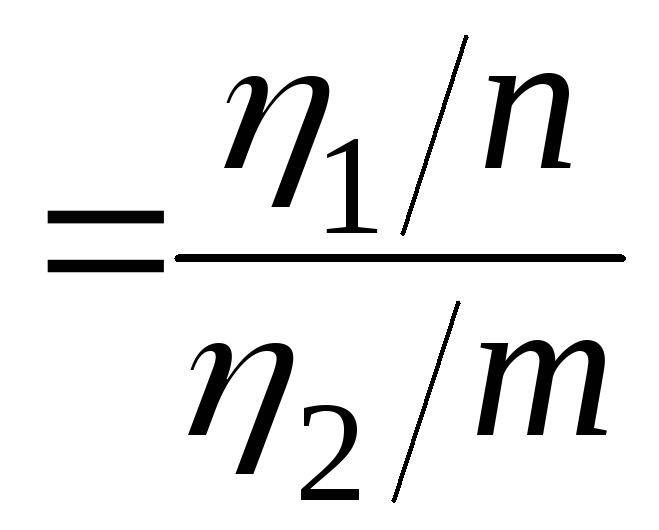
Распределение Фишера. Пусть ₁ и ₂ независимы и ₁ χ_n², ₂ χ_m², т.е. распределены по χ² с n и m степенями свободы, соответственно. Тогда случайная величина   F_{n, m} , то есть имеет распределение Фишера с числом степеней свободы (n, m). Функция плотности этого распределения

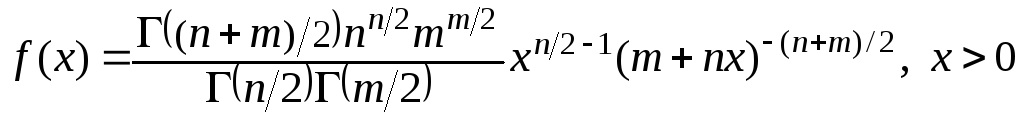. (3.3)

Математическое ожидание M = m/(m – 2), m > 2, мода , дисперсия D = .

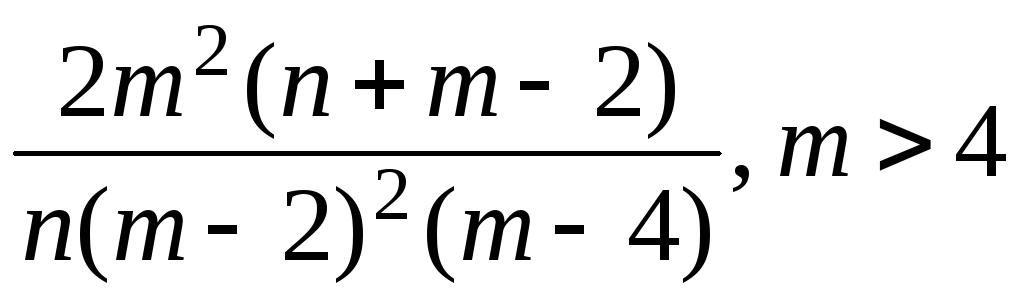Теорема о свойствах выборок из нормального распределения. Пусть

X = (x₁, x₂, …, x_n)  N(a,  ²). Тогда

1) 2) 3)Независимы.

Следствие. В условиях теоремы .

3.2 Интервальное оценивание параметров.

Пусть ξ  F(x,θ), θ  R – неизвестный параметр. Ставится задача определить лучший (в некотором смысле) интервал, содержащий значение θ с большой вероятностью.

Определение 3.1. Доверительным интервалом с уровнем значимости (уровнем доверия, доверительной вероятностью) 1 – α для неизвестного параметра θ по выборке X = (x₁,…, x_n) называется интервал (A(x₁,…, x_n), B(x₁,…, x_n)) такой, что

P{ A(x₁,…, x_n) < θ < B(x₁,…, x_n)} ≥ 1 – α.

Величина α здесь выражает вероятность возможной при решении данной статистической задачи ошибки, выбирается достаточно малой и из «посторонних» соображений.

Функции выборочных значений А и В называются доверительными границами и являются случайными величинами.

При больших объёмах выборок можно использовать также асимптотические доверительные интервалы, т.е такие, что

P{ A(x₁,…, x_n) < θ < B(x₁,…, x_n)} ≥ 1 – α.

Интуитивно ясно, и это несложно показать, что из требований несмещённости и эффективности оценки следует: при заданном α лучше выбирать симметричный относительно Mt_n и наиболее узкий, при прочих равных условиях, интервал вида Mt_n ± k·S_t . Здесь t_n – выборочная оценка параметра θ, S_t – его среднее квадратичное отклонение.