6.4.* Выборочные методы частного и множественного

корреляционного анализа.

Необходимо, также, несколько остановиться на задачах, возникающих при необходимости изучения множественной или частной корреляций на основе выборочных данных.

В первой части Практикума, посвящённой разделам теории вероятностей, рассматривались следующие соотношения для расчета коэффициентов частной и множественной корреляции.

Уместно напомнить, что вопрос о частной корреляции возникает тогда, когда требуется оценить наличие и/или степень статистической зависимости между двумя переменными при наличии ещё одного или целой группы других, сопоставимых по значимости для данной задачи с изучаемыми, переменных.

Вопрос же о множественной корреляции возникает при необходимости учёта статистической зависимости каждой из таких переменных от остальных и отсеивании малосущественных факторов.

a. Частная корреляция.

Таким образом, если мы имеем n-мерное невырожденное нормальное распределение и фиксируем n – 2 случайных величины, то получаем частную корреляцию оставшихся двух (скажем, x_p и x_q):

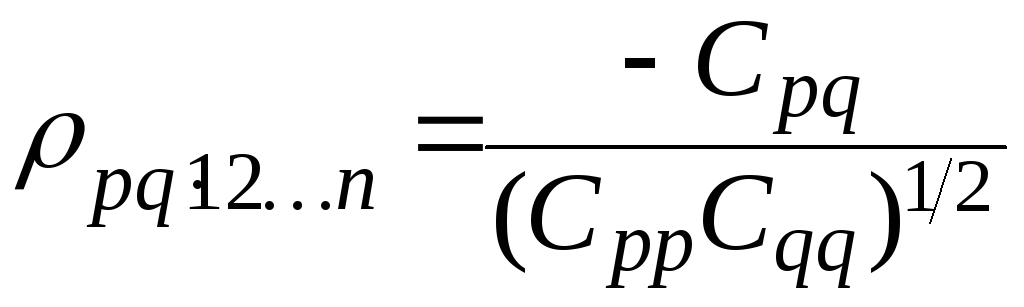, (6.62)

где –алгебраическое дополнение парного коэффициента корреляции в корреляционном определителе | C | = det C. В частности, при наличии всего трёх факторов, имеем, например

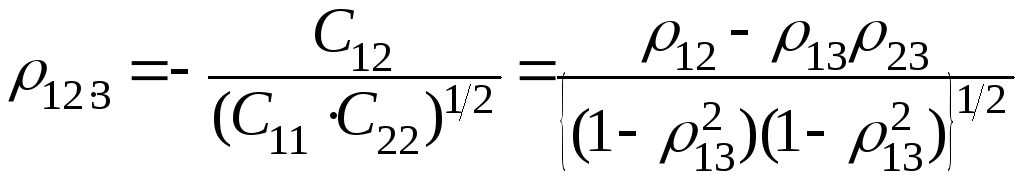
коэффициент частной корреляции между x₁ и x₂ при фиксированном x₃; ρ₁₂, ρ₁₃ и ρ₂₃ – соответствующие коэффициенты корреляции. При этом принято называть индексы p, q, 1 и 2 и им подобные называть первичными, а оставшиеся – вторичными. Если множество вторичных индексов достаточно велико, то его удобнее обозначать s_pq , а в коэффициентах, где первичные индексы и так выделены, в виде{s}(s – произвольное обозначение).

Линейная регрессия в этом случае имеет вид:

M(x_j|x₁, …, x_{j – 1}, x_{j + 1}, …, x_n ) = β₀ + β₁x₁ + … + β_nx_n, (6.63)

Где под β_k, k = 1, …, j – 1, j + 1, …, n понимаются частные коэффициенты регрессии β_jk•{q}.

Замечание 6.10. Полезно подчеркнуть смысл прилагательного «линейный» в общей модели линейной регрессии: она линейна относительно параметров β, но не обязана быть линейной относительно иксов; она вообще может включать в себя произвольные, а не только полиномиальные функции, например модель регрессии M(x₂|x₁, x₃) = β₀ + β₁x₁ + β₂x₁² + β₃ sinx₁∙sinx₃ + β₄x₃³ – линейная.

Для многомерного нормального случая имеем:

. (6.64)

Теперь займёмся вопросами оценки рассмотренных величин по заданной выборке объёма n. Подгонка регрессии осуществляется по методу наименьших квадратов, т. е. выбираем так, чтобы минимизировать сумму квадратов уклонений n наблюдений от подгоняемой регрессии:

, (6.65)

где n – объём выборки, p – число переменных; предполагается n > p. Следует заметить, что аппроксимация по методу наименьших квадратов, даёт те же коэффициенты регрессии, что и в случае точной линейной регрессии.

Если при заданной выборке объёма n мы подгоняем регрессии по методу наименьших квадратов, то все приводимые ранее соотношения для теоретических характеристик выполняются и для выборочных коэффициентов.

Заменяя в (6.64) теоретические коэффициенты регрессии на выборочные коэффициенты b и приравнивая квадратичную форму (6.64) выборочной оценке дисперсии ошибки (см. частьI Практимума) величины x_j относительно регрессии, получаем, после дифференцирования этого соотношения по и приравнивания производных нулю, (p – 1) уравнений вида

(6.66)

Как и в случае с теоретическими коэффициентами справедливо равенство и другие, связанные с этим соотношения. В общем случае, если рассматриваемаярегрессия линейна, то, как и в случае регрессий и корреляций нулевого порядка, выборочные коэффициенты b являются несмещёнными оценками соответствующих теоретических коэффициентов β, величины 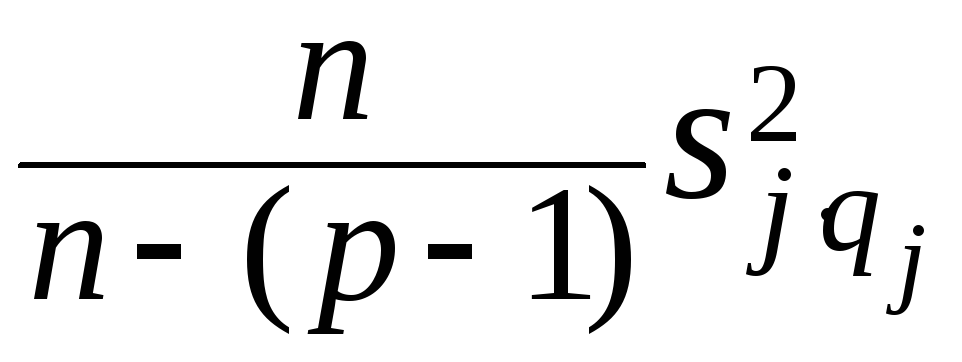, (выборочные оценки дисперсий ошибок подгоняемой регрессии) – несмещённой оценкой для соответствующих дисперсий; множество вторичных индексовсодержит в этих соотношениях (p – 1) различных значений.

Замечание 6.11. Из приведённых результатов следует, что вся совокупность частных регрессий, корреляций, а также дисперсий или ковариаций ошибок или остатков, полностью определяется дисперсиями и корреляциями или же дисперсиями и регрессиями нулевого порядка. Интересно дать геометрическую интерпретацию этому результату.

Предположим, имеется n наблюдений над p < n случайными величинами

x₁₁, …, x_1p; x₂₁, …, x_2p; x_n1, …, x_np .

Рассмотрим п-мерное (евклидово) выборочное пространство. Наблюдениям x_1k, …, x_nk над k-й случайной величиной соответствует в этом пространстве одна точка с соответствующими этим наблюдениям координатами. Следовательно, имеется p точек (по числу величин). Обозначим эти точки Q₁, Q₂, …, Q_p. Предположим, что иксы отличаются от своих средних и пусть точка P является началом координат.

Тогда величину nσ_l² можно интерпретировать как квадрат длины вектора PQ_l Аналогично, ρ_lm можно представить себе как косинус угла Q_lPQ_m, т.к.

,

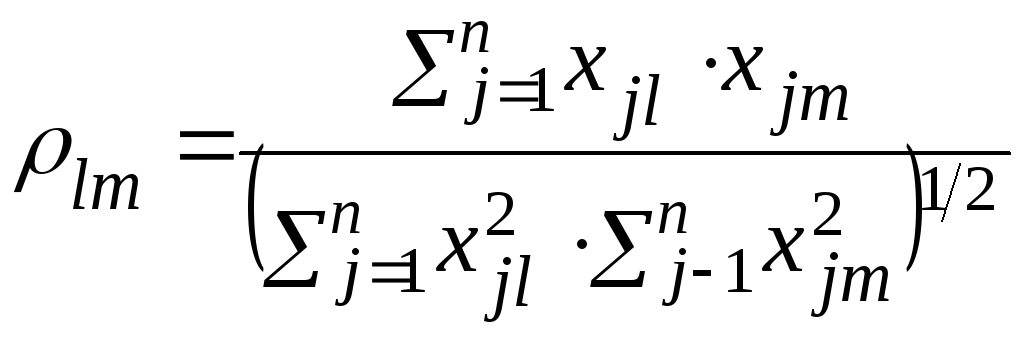а это и есть формула угла между векторами PQ_l и PQ_m.

Таким образом, все соотношения, связывающие p точек в n-мерном пространстве, могут быть выражены в терминах векторов PQ_i и углов между ними. То есть, можно сказать, что теория частной корреляции и регрессии формально тождественна с тригонометрией некоторой совокупности точек в n-мерном пространстве.

Касаясь вопроса о выборочных распределениях частных коэффициентов корреляции и регрессии, имеет смысл говорить о нормальном случае для генеральной совокупности. Для больших выборок, с очевидными изменениями, могут быть использованы стандартные ошибки, соответствующие коэффициентам нулевого порядка. Обозначая q множество вторичных индексов, имеем аналогично (6.6)

, (6.67)

а используя (6.63) можно получить

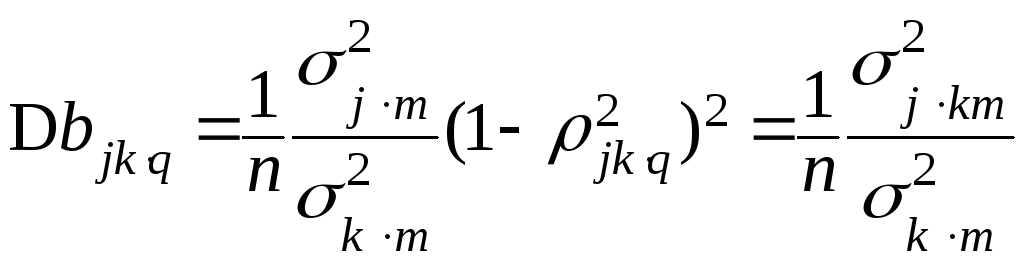. (6.68)

Для выборки объёма n точное распределение величины такое же как у парного («нулевого») коэффициента ,основанного на n – d наблюдениях, где d – число вторичных индексов множества индексов q, как следствие леммы Фишера о числе степеней свободы. Если d мало по сравнению с n, то распределение частных корреляций, когда n возрастает, по существу такое же как у коэффициентов нулевого порядка.

Для частных коэффициентов регрессии распределение коэффициентов нулевого порядка продолжает иметь место с заменой n на n – d, когда повсюду присоединено множество вторичных индексов q. В частности, статистика Стьюдента (6.28) для регрессии x _j по x_k превращается в

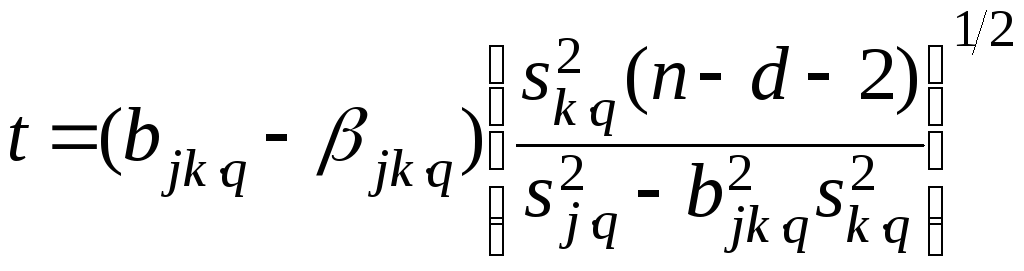(6.69)

с (n – d – 2) степенями свободы. Если множество q содержит все p – 2 оставшихся переменных, то число степеней свободы равно n – p.

b. Множественная корреляция.

Рассмотрим задачу линейной регрессии на случай p величин. Для p совместно нормальных величин x_j с нулевыми средними и дисперсиями σ_j² математическое ожидание величины x_m при условии, что x₁, …, x_{m – 1}, x_{m + 1}, …, x_p фиксированы, т. е. её регрессия по этим переменным, определяется соотношением (6.63). Дисперсия ошибка x_m относительно её регрессии по остальным переменным равна

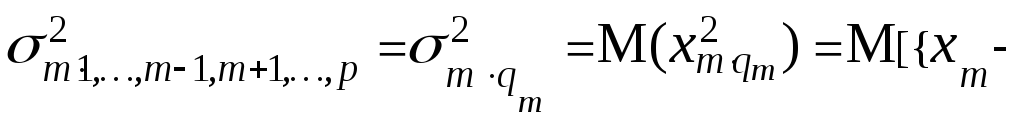
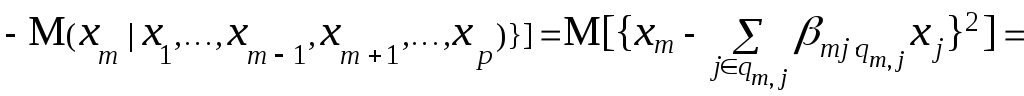(6.70)

,

где β_mj•q – частные коэффициенты регрессии; σ_mj – коэффициенты ковариации случайной величины x_m с остальными p – 1 переменными.

Можно показать, что M(x²_m•q) = M(x_m ∙x_m•q), то есть

= cov(x_m , x_m•q). (6.71)

Обычно о множественной корреляции говорят тогда, когда рассматривают корреляцию между случайной величиной x_m и её условным математическим ожиданием =x_m – x_m•q(q ≡ q_m – множество индексов других переменных, исключая x_m).При использовании(6.71), эта корреляция предстаёт в виде

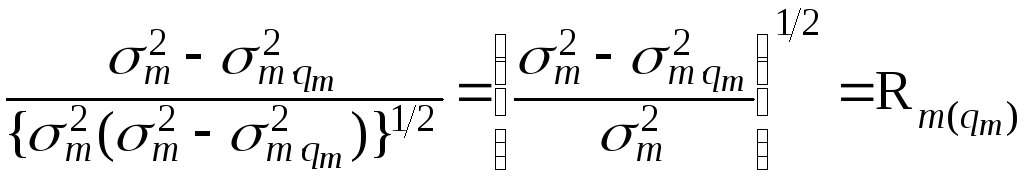, (6.72)

где и есть коэффициент множественной корреляции между случайной величиной x_m и другими p – 1 переменными. При этом следует заметить, что множество вторичных индексов q_m , а значит и соответствующее множество переменных, может содержать любое число элементов из p заданных, не совпадающих с x_m.

Полезны следующие соотношения:

1 – 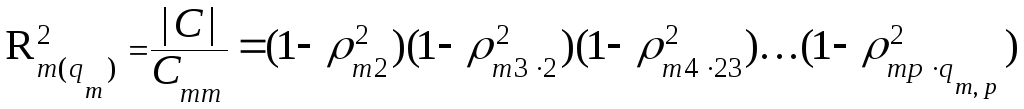,(6.73)

выражающие множественный коэффициент корреляции либо через корреляционный определитель, либо через частные корреляции.

Так как в (6.73) допустима перестановка всех индексов, кроме m, то из этого соотношения следует 1 – ≤ 1– ρ²_mj•s, гдеρ²_mj•s–произвольный частный или нулевого порядка коэффициент, содержащий m среди первичных индексов. Таким образом ≥| ρ_mj•s |,т.е. множественный коэффициент корреляции не меньше, чем абсолютная величина любого коэффициента корреляции с таким же первичным индексом. Если = 0, то из этого следует, что и все соответствующие ρ_mj•s = 0. В таком случае величина x_m полностью некоррелирована со всеми остальными величинами. С другой стороны, если = 1,то по крайней мереодин из коэффициентов ρ_mj•sдолжен быть равен 1 для того, чтобы правая часть (6.73) обращалась в 0. В этом случае, из определения коэффициента множественной корреляции следует = 0, т.е. все точки в распределении величины x_m лежат на линии регрессии и x_m является строго линейно функцией от x₁, …, x_{m – 1}, x_{m +1}, …, x_p .

Таким образом, коэффициентесть мера линейной зависимости величины x_m от x₁, …, x_{m – 1}, x_{m +1}, …, x_p .

Выборочный коэффициент множественной корреляции R_m(q) определяется соотношением, аналогичным (6.72) с соответствующей заменой теоретических статистик на их выборочные оценки:

1 – R²_m(q) = s²_m•q /s_m². (6.74)

Все приведённые ранее соотношения остаются в силе с заменой ρ на r, σ на s, β на b.

В связи с необходимостью проверки различных гипотез о характере и свойствах множественной корреляции, возникает вопрос о выборочном распределении R². Так как значения этого коэффициента не зависят от расположения и масштаба, то его распределение не будет зависеть от параметров расположения и масштаба.

Если рассматривать условное распределение величины R², то, в условиях нормальности наблюдённых величин, отношение

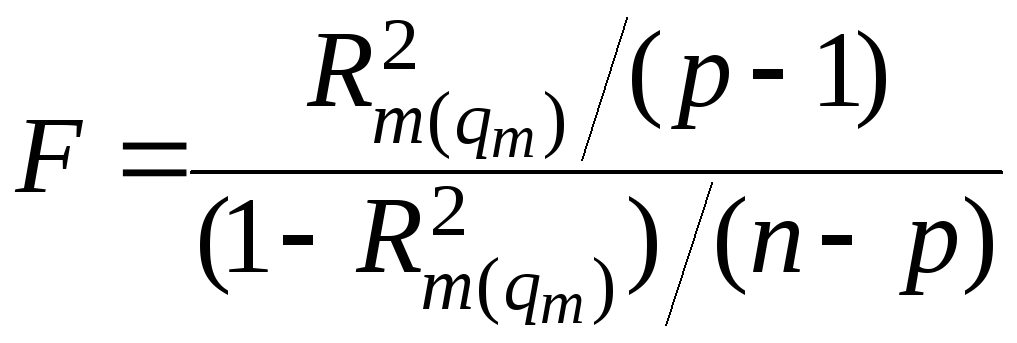(6.75)

имеет F-распределение Фишера с (p – 1, n – p) степенями свободы, где n > p – объём (максимальный объём) выборок.

Соотношение (6.75) представляет собой пример критерия отношения правдоподобия (ОП) для линейной гипотезы. Постулируется, сто среднее значение наблюдений над x_m является линейной функцией от p – 1 других величин с p – 1 коэффициентами плюс постоянный член, так что всего имеется p параметров. Проверяется гипотеза о том, что все p – 1 коэффициента равны нулю, т.е. H₀: R² = 0. Если гипотеза H₀ неверна, то величина F в (6.75) подчинена нецентральному F-распределение с (p – 1, n – p) степенями свободы и параметром нецентральности λ = nR². Рассмотренный критерий является РНМ инвариантным критерием.

Задача получения безусловного распределения R² весьма сложна, хотя в нормальном случае и разрешима. Для многомерного нормального случая с R² = 0 получается бета-распределение

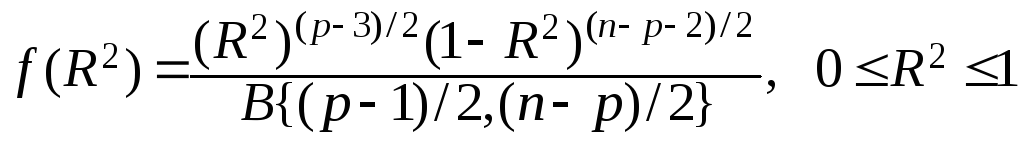(6.76)

В общем случае получается довольно громоздкое выражение, выраженное к тому же через гипергеометрическую функцию. Отметим лишь, что при n → ∞ безусловное распределение nR² (как и условное) сходится к нецентральному хи-квадрат распределению.

Как показал Уишарт, среднее значение величины R² в многомерном нормальном случае равно

.

В частности, когда = 0, (6.76) сводится к (6.77)

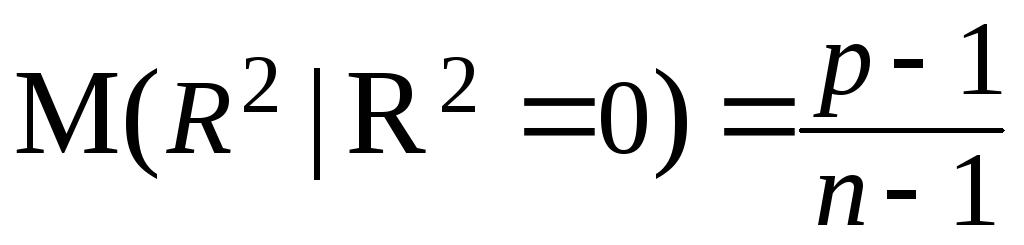, (6.78)

что можно получить и из (6.76).

Для дисперсии справедливы соотношения: при = 0

. (6.79)

Тот же результат можно получить из (6.76). При соотношение для дисперсии представимо в виде

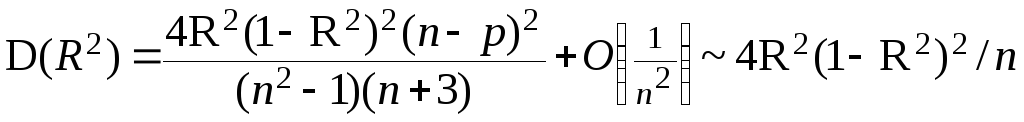. (6.80)

Таким образом, выборочная оценка R² является состоятельной, но, как это видно из (6.78), смещённой оценкой для .Для больших n M(R²) → R², а D(R²) → 0. При R ≠ 0 распределение величины R² асимптотически нормально со средним R² и дисперсией (6.80). Идиллия нарушается при R = 0. Распределение коэффициента R здесь существенно отличается от нормального, а дисперсия имеет порядок n ^{– 2} .

Распределение коэффициента R ведёт себя в отношении предельной нормальности аналогично распределению R², хотя его дисперсия всегда имеет порядок 1/n. Это следует из (6.78):

DR ~ (1 – R²)²/n . (6.81)

Это выражение совпадает с асимптотическим выражением для дисперсии обычного коэффициента корреляции при замене R на ρ. Естественно применить к R стабилизирующее дисперсию z-преобразование: z = arcth R. Но это опять же неприменимо вблизи R = 0, т.к. там нарушается (6.81), хотя порядок у дисперсии тот же:

DR = M(R²) – {M(R)}² ~ (p – 1)/n . (6.82)

Можно ли получить несмещённую оценку коэффициента для R² в многомерном нормальном случае? Как показали Олкин и Прэтт, формально – да.

Они получили статистику

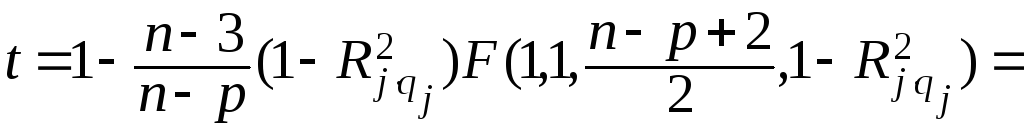
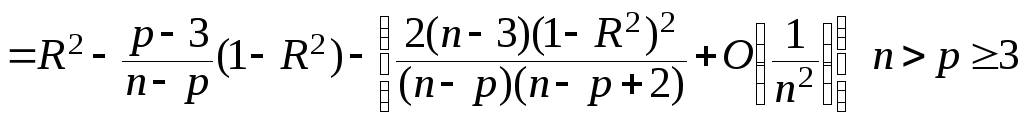, (6.83)

которая, являясь несмещённой оценкой от R², удовлетворяет условию t ≤ R². При R² = 1 имеем t = 1, но когда R² мало или равно нулю, то t - отрицательно, хотя имеющая смысл оценка для неотрицательной величины R² не может быть отрицательной. Таким образом, оценка (6.83) абсурдна.