1.2 Выборочные числовые характеристики.

Рассмотрим конкретные оценки параметров распределения случайной величины . Во всех следующих утверждениях считаем, что если рассматривается оценка момента или центрального момента порядка, то у случайной величиныконечен момент порядка

a. Выборочное среднее. В качестве оценки для математического ожидания используется оценка

, (1.3)

Которая называется выборочным средним.

Замечание 1.7. Выборочное среднее является средним значением (мат. ожиданием) для эмпирической функции распределения. Следует помнить, чтосама зависит от случая, т.е. каждому значению случайной выборки отвечает своя реализация эмпирической функции распределения. Рассматривая эту реализацию, как обычную функцию распределения, мы можем вычислить среднее той с.в., которая ей соответствует. Эта с.в. принимает значения (если их упорядочить)с равными вероятностями. Среднее же этой дискретной с.в. по определению равнот.е. равно выборочному среднему.

Замечание 1.8. Для выборочного среднего очевидно следующее равенство

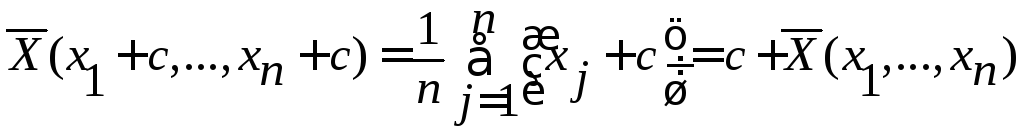
b. Выборочная дисперсия.В качестве оценки для дисперсии используется оценка

(1.4)

которая называется выборочной дисперсией.

Выборочная дисперсия характеризует среднеквадратичное отклонение выборочных величин от выборочного среднего.

Величина называетсявыборочной оценкой среднего квадратичного отклонения

Замечание 1.9. Для различных вычислений часто бывает удобней пользоваться следующей формулой для выборочной дисперсии:

(1.5)

с. Выборочные моменты.

Определение 1.14. Выборочным моментом порядка , построенным по выборке , называется величина.

(1.6)

Аналогично случаю с выборочным средним легко убедится, что выборочный момент порядка является моментом порядкадля эмпирической функции распределения.

Теорема 1.2. Выборочное среднее является несмещённой состоятельной оценкой момента.

Определение 1.15. Выборочным центральным моментом порядка , построенным по выборке, называется величина

(1.7)

Теорема 1.2. Выборочный центральный момент является инвариантной относительно сдвига несмещенной состоятельной оценкой (см. § 2) центрального момента.

Помимо оценок математического ожидания и дисперсии, часто используются выборочные оценки асимметрии, эксцесса, моды и медианы. Ниже приведены соотношения, задающие наилучшие, в определенном смысле, выборочные оценки этих параметров:

• выборочный коэффициент асимметрии

; (1.8)

а также можно использовать соотношение , где– выборочная оценка медианы распределения;

• выборочный коэффициент эксцесса

(1.9)

• выборочная оценка медианы – выборочное значение (варианта), делящее выборку (вариационный ряд) на две части, равные по числу выборочных значений (вариант)

2. Точечное оценивание параметров распределений

2.1 Свойства оценок; неравенство Крамера – Рао.

Пусть - случайная выборка, отвечающая случайной величине с функцией распределенияF_ξ (x,θ) , где - некоторый неизвестный параметр, характеризующий распределение случайной величины(например,- математическое ожидание). Параметр может быть как одномерным, так и многомерным.

Определение 2.1. Оценкой неизвестного параметра по случайной выборкеназывается любая функцияθ* = t_n (X), в том или ином смысле приближающая θ.

Очевидно, любая выборочная оценка t_n (X), которая является случайной величиной.

Определение 2.2. Оценка t_n (X) называется состоятельной оценкой параметра , еслиt_n (X) → θ по вероятности при .

Состоятельность означает, что с ростом объёма выборки качество оценки улучшается.

Состоятельность оценок определяется с помощью неравенства Чебышева:

P{|t_n – θ| < ε} < D[t_n]/ε².

Определение 2.3. Оценка t_n (X) называется несмещённой оценкой параметра , еслиM(t_n (X)) = θ. Если M(t_n (X)) → θ при n → ∞, то оценку t_n (X)

называют асимптотически несмещённой. Величина M(t_n (X)) – θ называется смещением оценки.

Определение 2.4. Оценка ν_n(x) называется эффективной оценкой параметра θ, если она обладает минимальной дисперсией M(t_n(x) – θ)² среди всех других оценок этого параметра.

Эффективные оценки являются наиболее точными, к их отысканию следует стремиться. Одним из наиболее мощных подходов к решению этой основан на применении неравества Рао – Крамера:

(2.1)

Это неравенство задаёт минимальную границу дисперсии (МГД) оценки функции τ(θ) параметра θ .

Определение 2.5. Оценка, дисперсия которой при всех θ равна МГД, называется МГД-оценкой.

Условие существования МГД-оценки:

дlogL/дθ = A(θ)·{t_n – θ},

где A(θ) – величина, не зависящая от наблюдений x_j , но, возможно, являющаяся функцией θ.

Определение 2.6. Оценка t_n (X) называется инвариантной относитель-

но сдвига (безразличной к сдвигу), если

Теорема 2.1. Выборочное среднее _, определяемое соотношением (1.3), является несмещенной состоятельной оценкой математического ожидания .

Теорема 2.2. Выборочная дисперсия , определяемая соотношением(II.1.4), является инвариантной относительно сдвига, несмещённой, состоятельной оценкой дисперсии .

В определении выборочной дисперсии множитель взят вместо множителядля того, чтобы добиться свойства несмещённости оценки.

Если моменты распределения рассматриваются как неизвестные параметры распределения генеральной совокупности, то соответствующие выборочные моменты являются несмещёнными оценками для них.