4. Расчёт числовых характеристик вариационных рядов

Меры центральной тенденции

Наиболее употребительной величиной такого типа является математическое ожидание, наилучшей выборочной оценкой которого служит арифметическое среднее.

Комментарий 1.8: Наилучшая оценка – означает устойчивую (робастную), состоятельную, несмещённую, наиболее эффективную оценку по имеющимся выборочным данным.

Выборочное среднее вычисляется по формуле

,

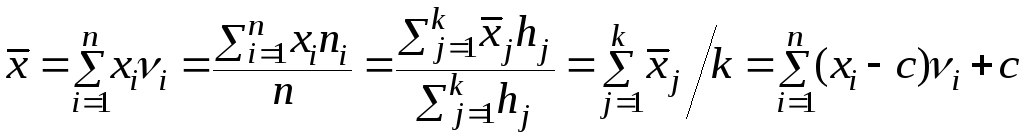Где h_j размер отдельного частичного интервала; –среднее значениеварианты в этом интервале (это – середина интервала, если в пределах частичного интервала все значения варианты полагаются равновероятными) ; k – число частичных интервалов; с – произвольная константа.

Комментарий 1.9: Формула расчёта выборочного среднего задана о всех вариантах, позволяющих рассчитать эту величину как по всей выборке, так и после её группирования, причём возможен выбор и различных по размеру частичных интервалов и даже предположение о различном характере распределений варианты на разных интервалах. В случае «сырой», необработанной выборки, следут напрямую воспользоваться первым выражением в этой формуле, положив все ν_i = 1/n . Последнее выражение в этой формуле позволяет упростить вычисления уменьшив все значения варианты на одно и то же удобное число.

В данном случае получаем (используем данные табл.3) = (12,15·0,02 + 12,45·0,06 + 12,75·0,08 + 13,05·0,1 + 13,35·0,35 + 13,65·0,21 + 13,95·0,09 + 14,25·0,07 + 14,55·0,02 = (– 1,2·0,02 – 0,9·0,06 – 0,6·0,08 – 0,3·0,1 + 0·0,35 + 0,3·0,21 + 0,6·0,09 + 0,9·0,07 + 1,2·0,02) + 13,35 =13,398 ≈ 13,40.

Другой часто используемой мерой центральной тенденции является

мода – значение случай ной величины имеющее наибольшую вероятность. Поэтому выборочной оценкой моды служит значение признака (варианты), имеющее наибольшую частоту. Так как модальный интервал (после приведения вариационного ряда к интервальному виду) проявляется обычно вполне отчётливо, то в качестве моды обычно принимвют середину этого интервала. При достаточно «широких» частичных интервалах, когда частота, в частности модального интервала, довольно велика и предположения о равномнрном распределении варианты в пределах этого интервала не вполне обоснованы,то значение моды можно уточнить по формуле (приближённой):

,

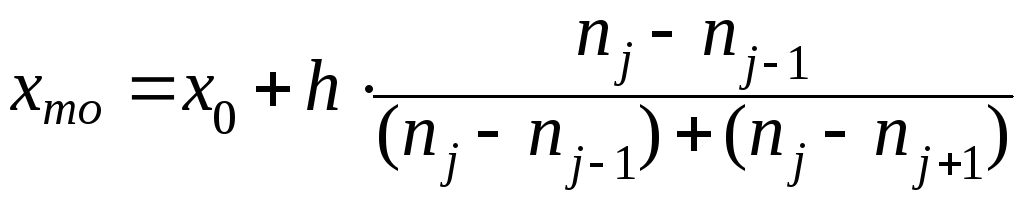где x₀ – начало модального интервала; h – длина модального интервала; n_j;

n_{j –1}; n_{j + 1} – частоты модального, предшествующего модальному и последующего после модального интервалов.

По данным задачи = 13,2 + 0,3[(35 – 10)/{(35 – 10) + (35 – 21)}] ≈13,392 ≈ ≈ 13,39.

Ещё одной полезной и часто используемой мерой центральной тенденции является медиана – такое значение случайной величины, что вероятности попадания этой случайной величины в интервалы значений больших или меньших медианного одинаковы и равны 1/2. Выборочная медиана – это значение признака, которое делит вариационный ряд на две части, равные по числу вариант.

Обычно, медиану сравнительно легко можно определить после упорядочения и ранжировки выборки. При работе с интервальным рядом для получения выборочной оценки можно воспользоваться формулой:

,

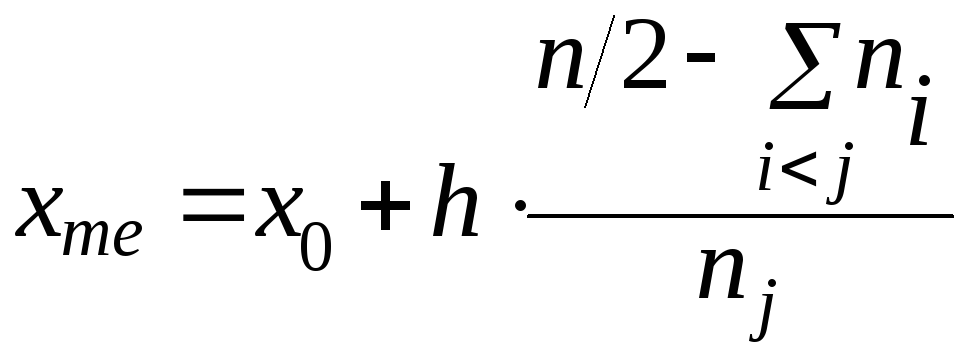где x₀ – начало медианного интервала; h – длина медианного интервала; n – объём выборки; n_j – частота интервала, содержащего медиану; Σ n_i – сумма частот интервалов, предшествующих медианному (можно заменить суммой частот интервалов, последующих за медианным).

В данной задаче: по ранжированному ряду =13,40; медианный интервал – пятый, с частотой n₅ = 35 и средним значением варианты x₅ = 13,35; уточнение по формуле даёт= 13,2 + 0,3[50 – (2 + 6 + 8 +10)]/35 ≈13,406≈ 13,41.

Комментарий 1.10: В рассматриваемой задаче все три меры центрвльной тенденции практически совпадают (± 0,01 от выборочного среднего), что указывает как на симметричность распределения генеральной совокупности, так и на представительность данной выборки.

Меры изменьчивости (характеристики рассеяния)

Речь идёт о величинах, позволяющих оценить разброс значений случайной величины (то же – для выборочных значений) относительно рассмотренных выше характеристик центральной тенденции.

Самой простой из таких характеристик является размах – разность максимального и минимального значений признака. Для случайных величин, в подавляющем большинстве случаев определённых на бесконечном или полубесконечном интервалах, эта характеристика малопригодна. Зато при анализе выборочного материала необходима вседа. Таким образом, для выборки

Размах R = x_max – x_min . В данной задаче R = 14,51 – 12,01 = 2,50.

Основными характеристиками рассеяния являются дисперсия D и среднеквадратичное (стандартное) отклонение σ. Выборочные оценки этих характеристик находятся по формулам:

; .

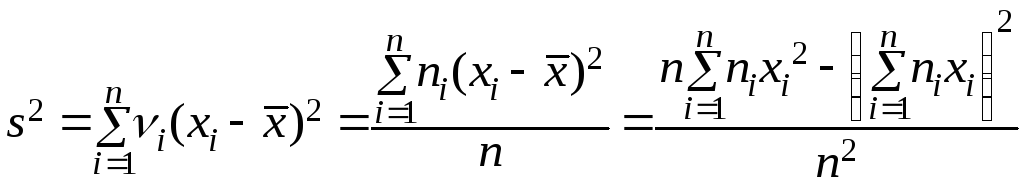Так как выборочная оценка дисперсии является смещённой (точнее, асимптотически несмещённой), то для малых выборок (n < 50) делают поправку на сиещение. Исправленная оценка дисперсии имеет вид

.

В данной задаче получаем

=(12,15² ·0,02 + 12,45² ·0,06 + 12,75² ·0,08 + 13,15² ·0,1 + 13,35² ·0,35 + 13,65² ·0,21 + 13,95² ·0,09 + 14,25² ·0,07 + 14,55² ·0,02)/100 – (13,40)²/100²= [(2·1,2² ·0,02 + 0,9² ·0,13 + 0,6² ·0,17 + 0,3² ·0,31)·100 – (0,048)²]/100² ≈0,2532;

≈;s ≈ 0,05.(0,5676)

Найдём также для нашей выборке коэффициент вариации:

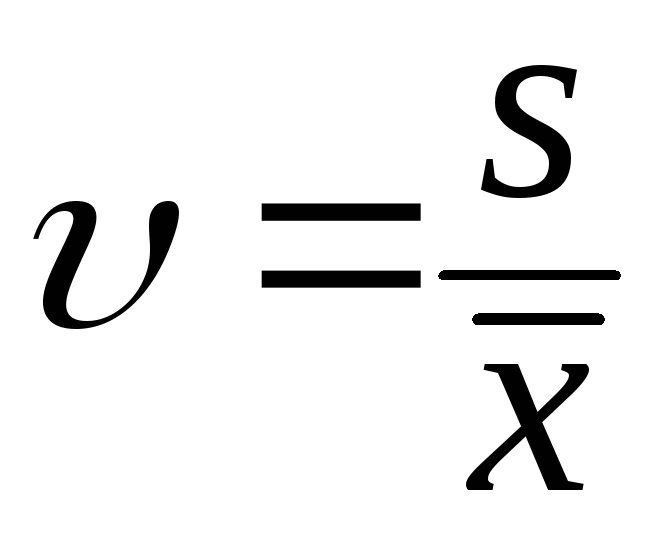=0,5/13,40 ≈ 0,037.

Меры формы распределения (асимметрия и эксцесс)

Асимметрия As распределения характеризует симметричность формы кривой плотности распределения (её крутизну, скошенность) относительно модального значения. Обычно эти меры также относятся к мерам изменчивости.

Эксцесс Ex распределения характеризует форму плотности распределения (островершинность) в окрестности модального значения.

Для описания этих характеристик используются центральные моменты третьего и четвёртого порядков:

As(ξ) = μ₃/σ³; Ex(ξ) = μ₄/σ⁴ = μ₄/(Dξ)².

Выборочные оценки этих характеристик задаются соотношениями (1.8) и (1.9)

• выборочный коэффициент асимметрии

;

а также можно использовать соотношение , где=x_me – выборочная оценка медианы распределения;

• выборочный коэффициент эксцесса

В данном случае As = 3·(13,398 – 13,406)/0,5 ≈ 0,48 ≈ 0,5.

Ex = [(12,15 – 13,40)4 ·0,02 + (12,45 – 13,40)4 ·0,06 + (12,75 – 13,40)4 ·0,08 + (13,15 – 13,40)4 ·0,1 + (13,35 – 13,40)4 ·0,35 + (13,65 – 13,40)4 ·0,21 + (13,95 – 13,40)4 ·0,09 + (14,25 – 13,40)4 ·0,07 + (14,55 – 13,40)4 ·0,02] /(0,5)⁴ – 3 = [1,254 ·0,02 + 0,954 ·0,06 + 0,654 ·0,08 + 0,054·0,035 + 0,254 ·0,31 + 0,554·0,09 + 0,854·0,07 + 1,154·0,02]/(0,5)⁴ – 3 ≈ 5,84 – 3 = 2,84.

На основании уже полученных результатов можно предварительно полагать, что выборка представляет собой случайную величину с достаточно симметричным распределением, обладающую очень малой дисперсией (как следствие большой эксцесс распределения). В таком варианте она достаточно далека от нормального распределённой случайной величины.

ЗАДАНИЕ 1.2

Предполагая, что рассматривая нами выборка представляет собой нормальное распределение, рассчитаем оптимальные доверительные интервалы

для математического ожидания и дисперсии этого распределения.

Напомним, что доверительным называется интервал, который с заданной надёжностью γ покрывает оцениваемый параметр.

Доверительный интервал для математического ожидания при неизвестной дисперсии, поэтому используется её выборочная оценка (см. 3.5):

,

где s – среднее квадричное отклонение; m = M–оцениваемоематематическоеожидание. Поправочные коэффициенты t_γ находим из

таблицы Приложения VII (квантили распределения Стьюдента), как корни уравнения T(n – 1,t_γ) = 1 – γ при заданном n. В данном случае n = 100; для γ = =0,95 находим t_γ = 1,984; для γ = 0,99 находим t_γ = 2,626. Так как = 13,398; а s = 0,50, то в итоге получаем:

при γ = 0,95 13,299 < m < 13,497; при γ = 0,99 13,267 < m < 13,511.

Доверительный интервал для среднего квадратичного отклонения при неизвестном математическом ожидании, вместо которого используется его выборочная оценка, получается извлечением квадратного корня из границ доверительного интервала для дисперсии (см. (3.7)):

(n – 1)s²/q₂ < σ² < (n – 1)s² /q₁,

где s – среднее квадричное отклонение; q₁ и q₂ находим из таблицы Приложения VI (квантили хи-квадрат распределения), как корни уравнений χ²(n – 1, q₂) = 1 – γ/2; χ²(n – 1, q₂) = γ/2 при заданном n.

При n = 100; для γ = 0,95 находим q₁ = 98,452; q₂ = 128,809 и 0,193 < σ² < 0,259; для γ = 0,99 находим q₂ = 140,169; q₁ = 98,158 и 0,181 < σ² < 0,258.

Комментарий 1.11: Полученый результат лишний раз подтверждает, что данная случайная величина имеет распределение, далёкое от нормального: доверительный интервал для дисперсии, вообще говоря, не является симметричным и для нормального распределения, но не до такой же степени.

ЗАДАНИЕ 1.3

Используя критерий согласия хи-квадрат Пирсона при уровнях значимости γ₁ = 0,95 и γ₂ = 0,99 проверим гипотезу H₀ о том, что данная выборка получена из нормальной генеральной совокупности, параметры которой заданы выборочными оценками математического ожидания и дисперсии.

Рассчитаем статистику критерия, используя соотношение (4.3)

.

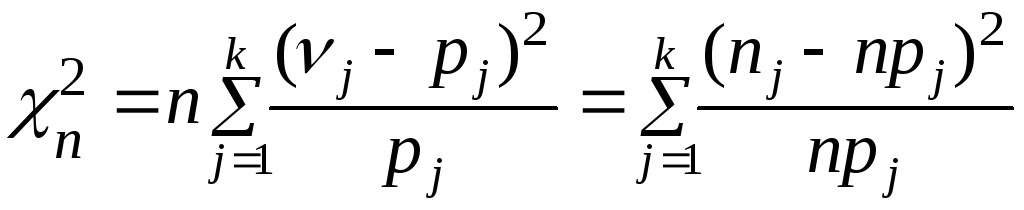В нашем случае, объём выборки n =100, число частичных интервалов

k = 9, но так как частоты крайних интервалов n₁ = n₉ = 2 < 5, их следует объединить с соседними. Представим изменённые данные в виде таблицы

Середина интервала xi	12,30	12,75	13,05	13,35	13,65	13,95	14,25
Нормированная величина yi	-2,16	-1,28	-0,70	-0,10	0,50	1,08	1,67
Вероятности	0,015	0,100	0,242	0,460	0,691	0,860	0,953
Относитель ноя частота νi	0,08	0,08	0,1	0,35	0,21	0,09	0,09
Теоретические частоты pi	0,004	0,076	0,340	0,421	0,145	0,014	0,0003

Теоретические частоты p_i находим по таблицы 4 Приложения IV(функция нормального распределения) для нормированной случайной величины y_i = (x_i – )/s.

Тогда χ² ≈ 100[(0,08 – 0,085)²/0,085 + (0,08 – 0,142)²/0,142 + (0,1 – 0,218)²/0,218 + (0,35 – 0,231)²/0,231 + (0,21 – 0,169)²/0,169 + (0,09 – 0,093)²/0,093 + (0,09 – 0,047)²/0,047] ≈ 0,089 + 2,679 + 6,389 + 6,129 + 0,995 + 0,010 + 3,956 ≈ 20,242.

Если критические значению χ² – критерия выбирать по полному объёму выборки n = 100, то χ²(99; 0,95) = 77,929; χ²(99; 0,99) = 70,065, и то и другое значительно превышают полученное значение статистики, что означает выполнимость нулевой гипотезы. Однако расчёты статистики критерия проводились по k = 7 значениям варианты. Поэтому правильнее искать критические значения статистики для k – 1 = 6 степеней свободы: χ²(6; 0,95) = 1,635; χ²(6; 0,99) = 0,872. Так как рассчитанное значение статистики критерия превышает критические значения, то гипотезу H₀ о нормальности распределения, из которого извлекалась выборка, следует отвергнуть.

ЗАДАНИЕ 1.4

Проверим, используя метод однофакторного дисперсионного анализа, однородность заданной выборки

Гипотеза H₀ утверждает, что это множество однородно – точнее, все наблюдения извлечены из одной генеральной совокупности, распределённой нормально с Φ(m, σ²). Альтернативная гипотеза говорит о том, что на множестве наблюдений действует хотя бы один посторонний фактор, что и вызывает расслоение множество наблюдений на неоднородные группы.

Статистика критерия для прверки нулевой гипотезы задаётся соотношением (5.3): если верна гипотеза H₀, то величина

,

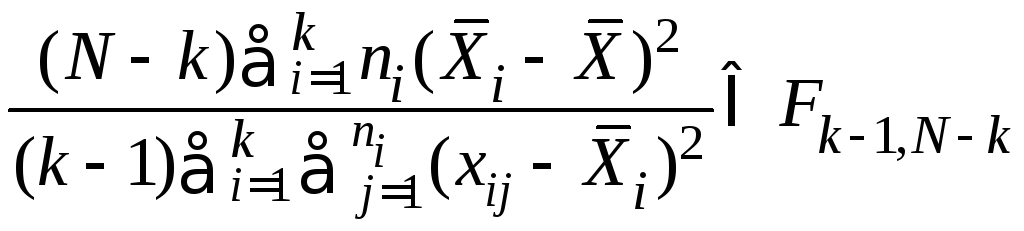имеет распределение Фишера с (k – 1) и (N – k) степенями свободы.

Задаваясь уровнем значимости гипотезы 1 – γ = 1 – q/100, по таблице распределения Фишера находим q – процентное критическое значение F_q . Гипотеза H₀ принимается с вероятностью 1 – γ, если выполняется неравенство F ≤ F_q.

Разобьём первоначальную (необработанную) выборку на 10 равных по объёму (это не обязательно, но упрощает процедуру) групп. Тогда в формуле статистики критерия N =100 – объём выборки; k = 10 – число групп; n_i – численности групп; x_ij – выборочные значения; – ощее средне– внутригрупповые средние.

j i	1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10	13,21 13,88 13,26 13,55 13,40 13,61 13,41 13,13 13,50 13,53 14,51 13,32 13,38 13,93 12,32 13,52 12,90 14,26 13,67 12,78 13,18 13,16 12,01 13,82 14,27 12,60 12,38 13,58 13,59 13,25 13,42 13,49 13,24 12,87 13,39 13,34 12,88 13,27 13,64 13,48 12,48 13,00 13,78 13,01 13,46 13,29 13,33 13,25 14,21 13,61 14,02 12,12 13,22 13,66 13,43 13,31 12,84 12,81 13,58 13,80 13,73 14,18 13,70 13,45 13,23 13,53 14,13 14,45 13,36 13,30 13,41 12,42 13,47 13,30 14,37 13,22 13,50 13,10 13,99 13,43 13,27 13,19 13,40 13,55 12,30 13,44 13,51 13,56 13,39 13,94 13,85 13,78 13,00 12,72 13,57 13,33 13,29 13,35 12,59 13,25	13,46 13,46 13,18 13,30 13,28 13,28 13,71 13,42 13,55 13,36	0,06 0,06 − 0,22 − 0,10 − 0,12 − 0,12 0,31 0,02 0,15 − 0,04

=0,215

Так как в нашем случае все n_i одинаковы и равны n/k = 10, то числитель в формулестатистики критерия равен 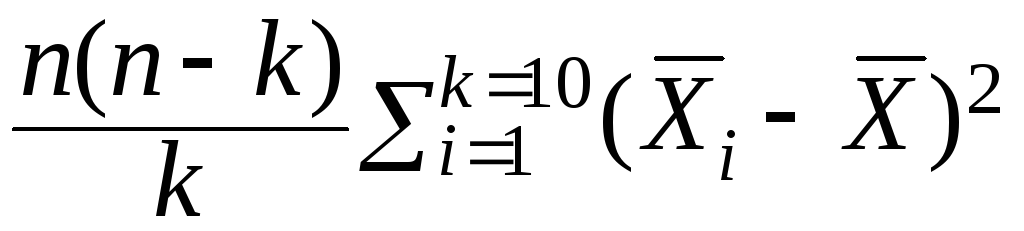= 900·(36 +36 + 484 + 100 + 144 + 144 + 961 + 4 + 225 + 16)·10^{– 4} = 193,5; а знаменатель представим в виде

–(k–1)=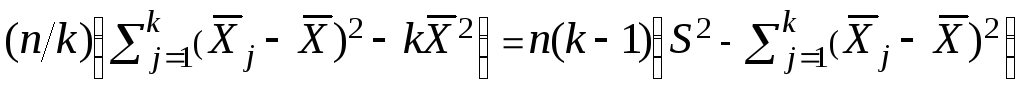

= 900·(0,2532 – 0,215) = 34,38.

Тогда расчётная статистика критерия F_{9, 90} = 193,5/34,38 = 5,628. По таблицам критерия Фишера для числа степеней свободы (k – 1); (n – k) = 9; 99 для уровней значимости γ₁ = 0,95 и γ₂ = 0,99 находим критические значения критерия F₁ = 1,906 и F₂ = 2,626. Так как расчётное F_{9, 90} > F₂ > F₁, то нулевую гипотезу в обоих случаях следует отвергнуть.

ЗАДАНИЕ 1.5

Предположем, что распределение генеральной совокупности, из которой извлечена наша выборка, подчинена распределению Вейбулла; F(x) = 1 – exp[–(x/b)^c], определим методом максимального правдоподобия (ММП) или методом моментов (ММ) параметры с и b.

Для применения ММП запишем функцию правдоподобия

.

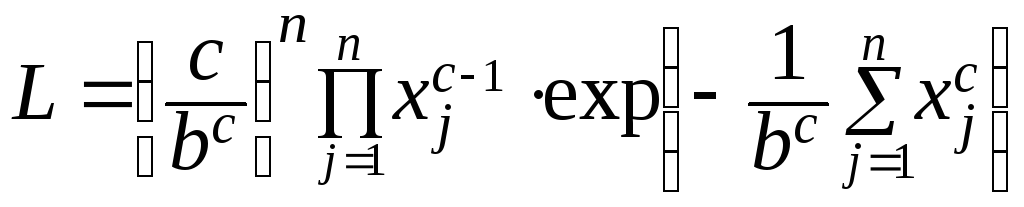Возмём частные производные по параметрам с и b от ln L и приравняем их нулю, в результате чего получим систему уравнений

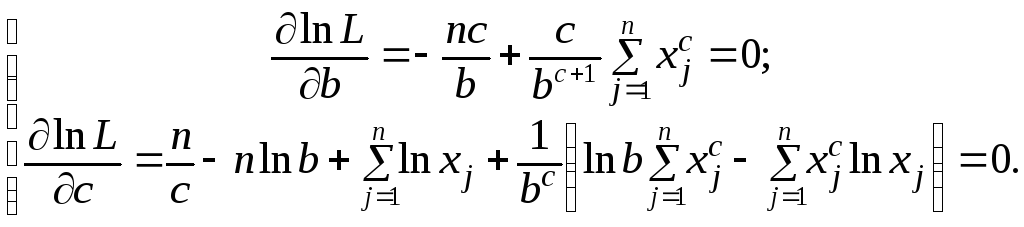
Преобразуя эту систему уравнений, получаем, что оценки c* и b* параметров

с и b по ММП, есть решения системы трансцендентных уравнений

Так как плотность распределения Вейбулла f(x) = (cx^{c – 1} /b^c)exp[– (x/b)^c], то используя определение гамма-функции Γ(υ) = несложно получить:Mξ = bΓ [(c + 1)/c]; Dξ = b²(Γ [(c + 2)/c)] – {Γ [(c + 1)/c]}². Заменяя в этих соотношениях математическое ожидание и дисперсию на их выборочные оценки, а параметры с и b на их оценки c* и b*, получаем систему уравнений для этих оценок по ММ:

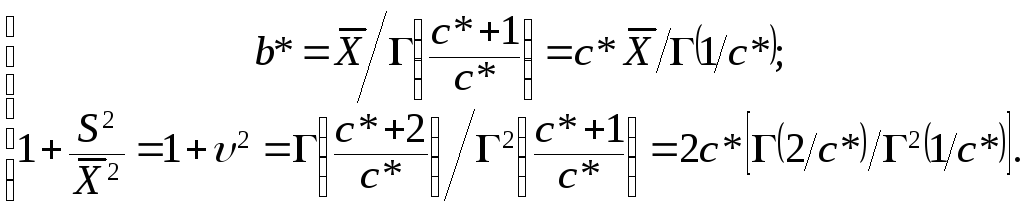
Так как коэффициент вариации для нашей выборки достаточно мал: υ = 0,037 и υ² = 0,001369 ≪ 1, то будем подбирать такую c*, чтобы левая часть второго уравнения равнялась 1.

В данном случае достаточно хорошим приближeниeм являeтся значeниe парамeтра c* ≈ 3; тогда b* ≈ 15.

Сравним теперь экспериментальное и гипотетическое распределения по критерию Смирнова (4.4):

ω² = 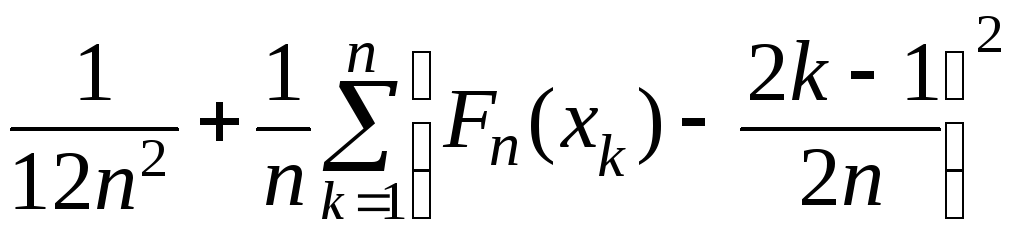. В данном случаеn = 8 – число интервалов вариационного ряда; значения x_k и F(x_k) = 1– exp[– (x_k /15)³] представлены таблицей:

xk	12,15	12,45	12,75	13,05	13,35	13,65	13,95	14,25	14,55
F(xk)	0,412	0,436	0,459	0,483	0,506	0,530	0,553	0,576	0,599

Выборочная статистика критерия Z_n = n ω² = 0,484; критические значения Z_0,01 = 0,736 при доверительной вероятности γ = 0,99 и Z_0,05 = 0,461 при доверительной вероятности γ = 0,95. По результатам исследования можно говорить, что распределение Вейбулла с параметрами c* ≈ 3; b* ≈ 15 неплохо апроксимирует выборочное распределение, хотя экспериментальная кривая немного выходит из критического интервала при γ = 0,95.

УПРАЖНЕНИЕ II.

ЗАДАЧА 2.1

Для контроля взяты 200 узлов, собранных на ученическом конвейере.

Исходные данные задачи заданы в двух первых строках таблицы,

i	0	1	2	3	4	5	6	7
mi	37	60	51	22	16	8	4	2	Всего 200
pi	0,135	0,271	0,271	0,181	0,090	0,036	0,012	0,004

где m_i, – число узлов, при сборке которых пропущеноiопераций. Используя в качестве оценки параметраa* медианное, модальное или среднее значение выборочной случайной величины, проверить по критерию хи-квадрат её согласие с распределением Пуассона.

Как следует из заданной таблицы модальное значение числа пропущенных операцй равно x_mod = 1; x_me = 2; x_ср = (1·60 + 2·51 + 3·22 + 4·16 + 5·8 + 6·4 + 7·2)/200 = 1,8. Используем в качестве оценки параметра a* медианное значение случайной величины, т.е. a*= 2. Запишем в третью строку таблицы полученные на этой основе «теоретические» частоты (Приложение IV: распределение Пуассона с плотностью ). Используя соотношение 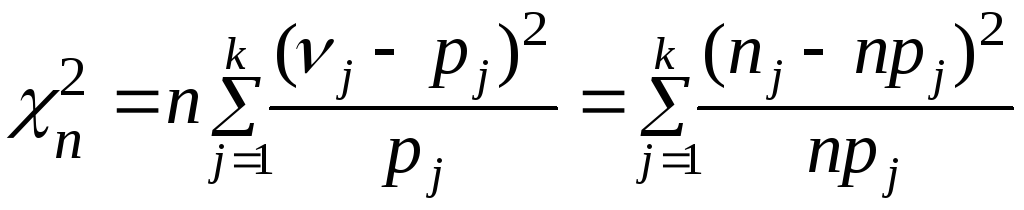, рассчитаем статистику критерия хи-квадрат для проверки нулевой гипотезы: = 13,18. Таким образом, предположение о Пуассоновском характере распределения представленной выборки случайной велисины согласуются ли по критерию² с уровнем значимости α = 0,05 {²_0,05(7) = 14,07 > = 13,18}, однако близость вычисленного и критического значений критерия не позволяют быть уверенным в статистической устойчивости полученной информации.

ЗАДАЧА 2.2Тысяча человек участвовала в соревнованиях по рыбной ловле. Из них m_i человек поймали i рыб, что представлено первыми двумя строками следующей таблицы:

i	0	1	2	3	4	5	6	7	8	9	10
mi (A)	437	250	138	80	49	16	10	8	6	3	3
mi (B)	531	220	109	69	40	11	9	5	4	1	1
pi a = 0,6	0,400	0,240	0,144	0,086	0,052	0,031	0,019	0,011	0,007	0,010
pi а*=0,5	0,500	0,250	0,125	0,063	0,031	0,016	0,008	0,004	0,003

С уровнем значимости α= 0,05 проверить гипотезу о показательном законе распределения случайной величины ξ, представляющем число пойманных рыб,P(ξ= i) = (1 –a)a ⁱ. Это следует сделать для заданного значения параметраaи для его оценкеa^*по одной из предложенных выборок (Aили B) или их комбинации.

Так как задача проверки гипотезы во всех случаях однотипна, то рассмотрим лишь её вариант с предварительной оценкой гипотезы по выборке В

Воспользуемся методом максимального правдоподобия (ММП). Функция правдоподобия по выборке объёма n: L = ; ln L = n ln(1 – a) + (ln a)·Σx_k ; 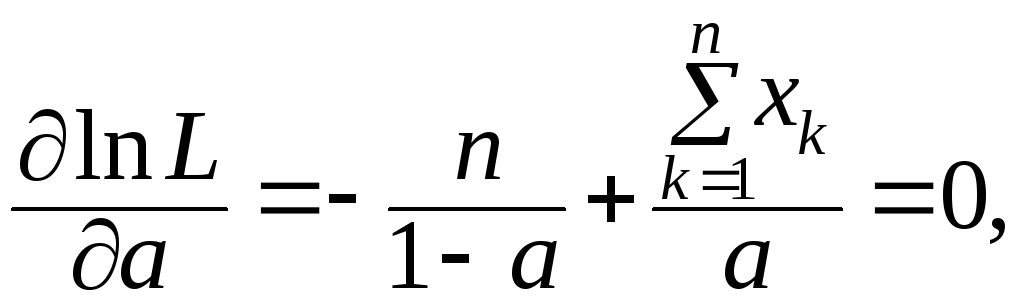откуда и оценка параметраа (вероятности «успеха» или «неудачи») 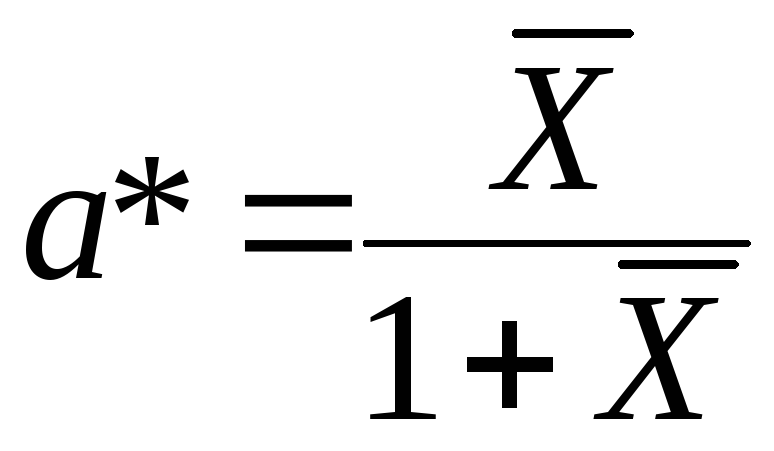, где- выборочное среднее арифметическое. Для выборкиВ имеем =(0·531 + 1·220 + 2·109 + 3·69 + 4·40 + 5·11 + 6·9 + 7·5 + 8·4 + 9·1 + 10·1)/1000 = 1,0. Тогда

a^* = ½ = 0,5.

Используя полученную оценку параметра рассчитаем «теоретические» чачтоты p_i и статистику критерия хи- квадрат: =(31²/500 + (-30)²/250 +

(-16)²/125 + 6²/63 + 9²/31 + (-5)²/16 + 1²/8 + 1²/4 + 3²/3) ≈ 15,645.

Комментарии: 2.1. При использовании критерия хи-квадрат интервалы, в которых наблюдённые частоты меньше 5 принято объединять с соседними.

2.2. Число степеней свободы критерия хи-квадрат ν = n – 1 (n – число интервалов в выборке) при заданных параметрах распределения и ν = n – т – 1, если т из них оценивается по выборке.

В данном случае по таблице квантилей хи-квадрат распределеня (Приложение IV) находим на пересечении столбца, в котором указан уровень значимости α = 0,05, и строки с укзанием числа степеней свободы ν = 9 – 1 =8, находим критическое значение статистики χ₇² (0,05) = 14,067.

Так как расчётное значение критерия хи-квадрат превышает его как критическое значениепри заданном уровне значимости, то гипотезу о воз- можности описания полученной выборки показательным законом распределения с таким значением параметра следует отвергнуть.

ЗАДАЧА 2.3 Из генеральной совокупности случайной величины ξ, распределённой по биномиальному законуP(ξ = k) = Р_n(k) = , (k= 0; 1; 2; …;n) извлечена выборкаобъёмаm: {x₁;x₂;…;x_m} = (2, 6, 5, 0, 12, 10, 3, 6, 7, 9). Найти методом моментов и методом максимального правдоподобия статистическую оценку независимого параметраpи показать её несмещённость и эффективность.

Параметр p – это вероятность осуществления в каждом из n независимых испытаний некоторого события А. Рассмотрим случайную величину ξ₁ число появлений собатия А в одно независимом испытании. Распределение ξ₁ дискретно и имеет вид: P(ξ₁ = 0) = 1 – p = 1 – θ; P(ξ₁ =1) = p = θ. Осуществляя серию из n независимых испытаний получаем реализацию простой случайной выборки , в которой x_i = 1, если событие произошло в

i-м опыте, x_i = 0, если не произошло.

Для применения метода максимального правдоподобия (ММП) необходимо составить функцию правдоподобия ,0 < θ < 1.

Прологарифмируем её: 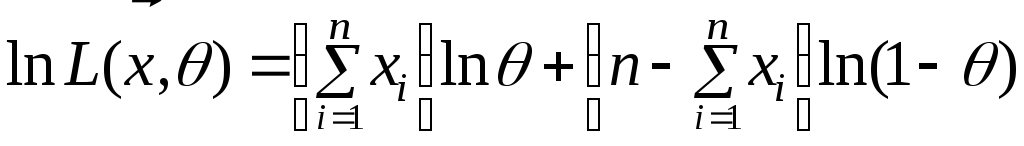; запишем уравнение правдоподобия:.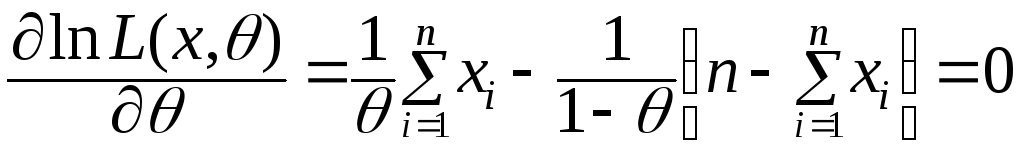

Получаем оценку максимального правдоподобия неизвестной вероятности наступления некоторого события в серии n независимых испытаний:

p* = θ* = ,

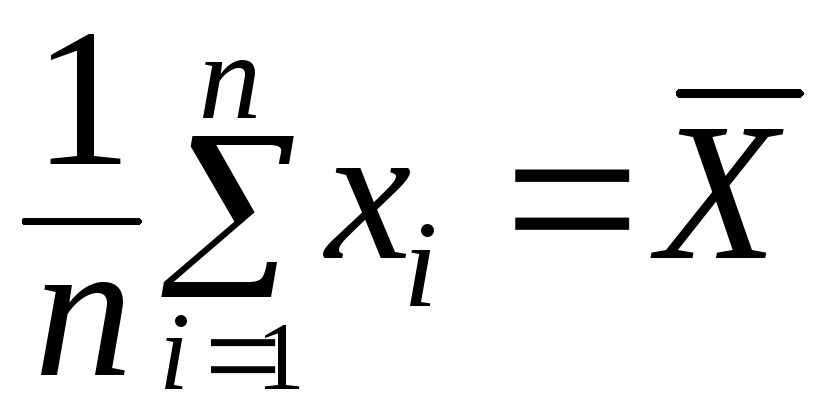где –среднее число «успехов» на одно испытание.

Аналогичный результат сразу следует из метода моментов (ММ): математическое ожидание случайной величины ξ,, имеющей биномиальное распределение, равно Mξ = np, где n – число независимых испытаний с бинарным исходом, p – неизвестная вероятность ненулевого исхода. Приравнивая математическое ожидание и его выборочную оценку 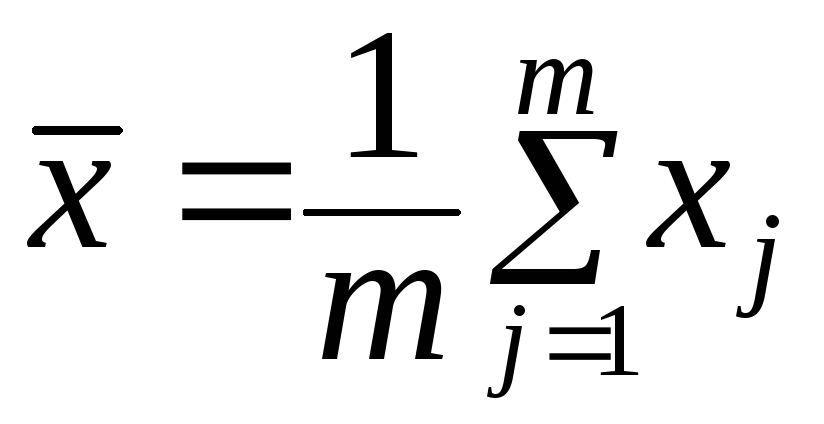, где m – объём выборки ( каждое значение x_j выборки есть число «успехов» в j – той серии из n независимых испытаний с бинарным исходом.

Общепринятой оценкой неизвестной вероятности «успеха» в серии n независимых испытаний по выборочным данным является величина

p* = θ* = /n, где –среднее число успехов.

Несмещённость этой оценкиследует уже из применения ММ.

Состоятельность следует из теоремы Бернулли: пусть k – число успехов в n независимых испытаниях с одинаковой вероятностью успеха p в каждом из них; тогда при любом ε > 0 .

Для доказательства эффективности оценки воспользуемся неравенством Крамера – Рао: 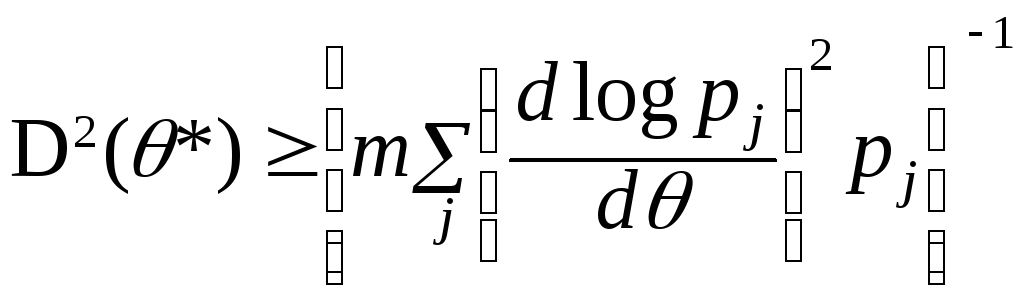; оценка эффективна если её дисперсия равна нижней границы неравенства. Здесьm– объём выборки; p_j – число успехов в в j– той серии из n независимых испытаний, соответсвующее j– му выборочному значению. Так как, гдеθ = p – оцениваемый параметр, то 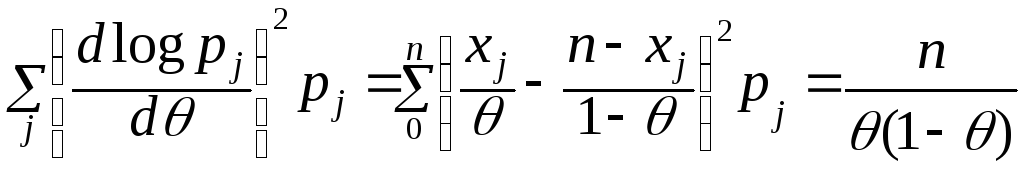. Таким образом, для несмещенной оценки .В частности, для p* = θ* = /n = 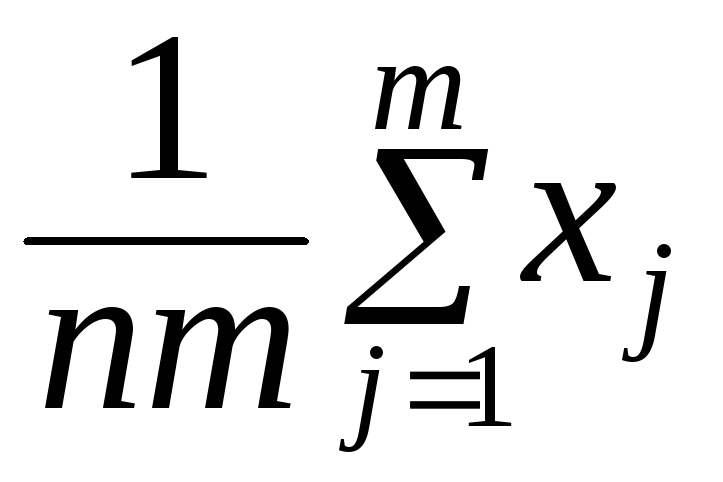получаем , так что эта оценка является эффективной.

Для заданной выборки =(2 + 6 + 5 + 0 + 12 + 10 + 3 + 6 + 7 + 9)/10 = 6

(m =10); судя по выборочным данным n ≥ 12, поэтому p* = θ* ≤ 6/12 = 0,5.

ЗАДАЧА 2.4 Используя предельное распределение Колмогорова (критерий Колмогорова), найти приближенно уровень значимости выборки A против гипотезы Н₀: Н₀ – экспоненциальное распределение с параметром, совпадающим с оценкой по выборке.Дать его традиционную интерпретацию.

«Теоретическое» экспоненциальное распределение задаётся функцией плотности распределения . Оценка неизвестного параметраλ по выборке объёма n (x₁, …, x_n) равна 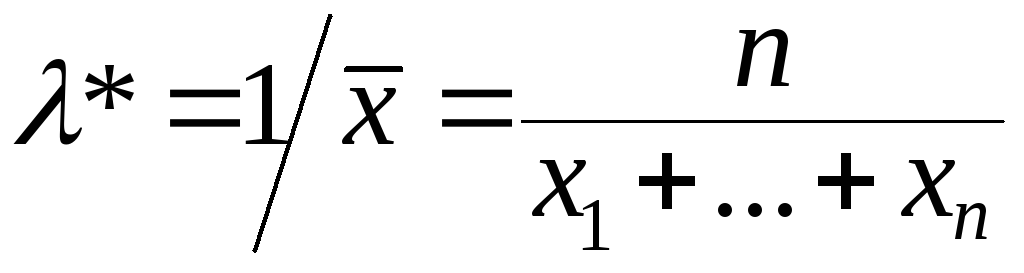(ММП). Пусть дана выборка (83, 83, 83, 82, 82, 81, 85, 84, 86, 81). Тогда = 83 иλ* = 1/83 ≈ 0,012. Составим таблицу, позволяющую сравнивать выборочные значения с гипотетическими «теоретическими»:

xi	81	82	83	84	85	86	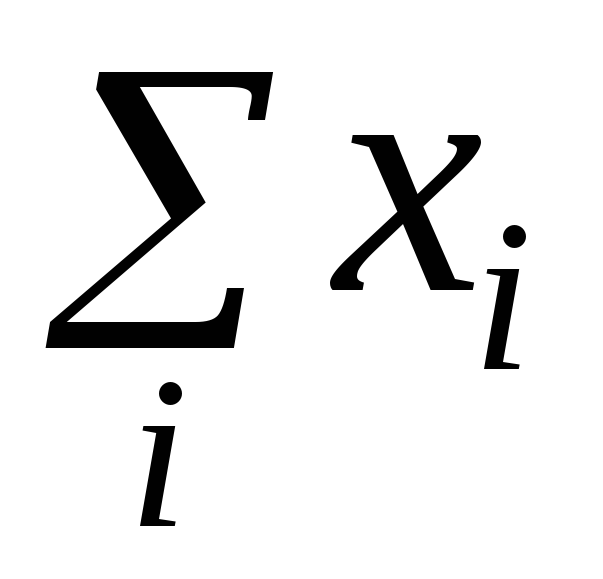=830
ni	2	2	3	1	1	1	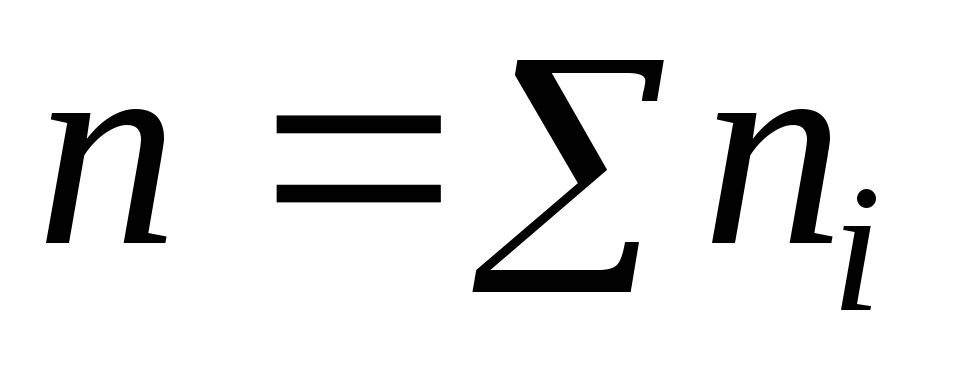=10
νi	0,2	0,2	0,3	0,1	0,1	0,1
F*n(x)	0,2	0,4	0,7	0,8	0,9	1,0
F(x)	0,621	0,624	0,632	0,637	0,641	0,645
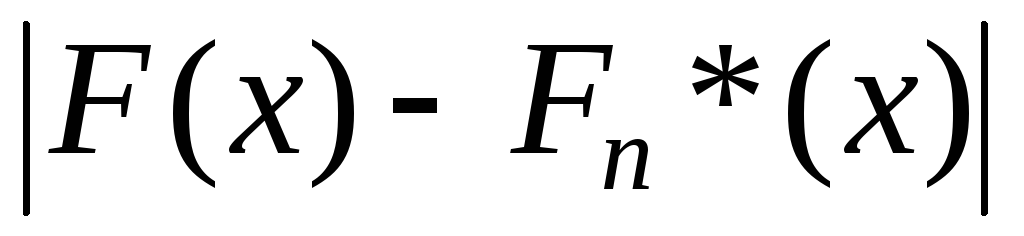
	0,421	0,224	0,068	0,163	0,259	0,355	Sup ΔF = 0,421

Статистикой непараметрического критерия Колмогорова является величина D_n= |F(x) –F_n*(x)| ≥d_n(α). Данная величина не зависит от вида распределения, но зависит отобъёма выборкиn иуровня значимостиα. При выполнении приведённого неравенства нулевая гипотеза отвергается. Так как случайная величинаz= (n)^1/2·D_nимеет асимптотическое (при бесконечном возрастанииn) распределение Колмогорова – функциюK (z). Уравнение для определения критического значения имеет вид:

.

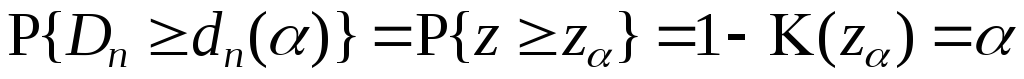Если воспользоваться двумя первыми членами разложения функции распределения Колмогорова

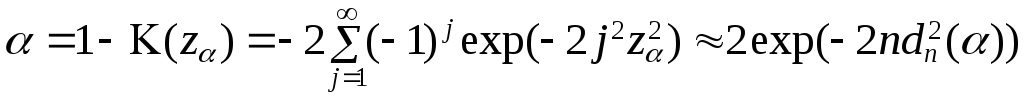, можно получить следующий вид выражения для границы критической областиd_n(α) = (ln(2/α)/2n)^1/2. Тогда получаем следующуюоценку уровня значимостиα выборкиАобъёмаn = 10 против гипотезыH₀(экспоненциальное распределение): α ≥ 2/(exp{2nd_n²}) ≈ 2/exp(20·0,421²) ≈ 0,055.

Примечание: Доказано, что использование распределения Колмогорова для практических расчётов оправдано уже при n ≥ 25 и α < 0,1. Кроме того, замена точных границ асимптотическими изменяет доверительный интервал d_n(α) в сторону увеличения надёжности критерия.

ЗАДАЧА 2.5 Дискретная случайная величина ξ имеет распределение P(ξ = x_m) = (1 – a)a ^m, m = 1, 2, …, 10. Используя метод моментов и метод максимального правдоподобия, получить точечные оценки параметра a по выборочным данным: варианты 1 ÷ 10 – по выборке A; варианты 11 ÷ 20 – по выборке B; варианты 21 ÷ 30 – по объединению выборок A и B.Примечание: в качестве выборочного материала используется положительные значения последних цифр этих выборок.

Решение этой задачи во многом идентично решению задачи 3с)и достатчно подробно прокомментировано выше при рассмотрении этой задачи.

УПРАЖНЕНИЕ III

Все задачи этого упражнения связаны сопределением точечных оценок параметров тех или иных распределений; расчётом доверительных интервалов для таких параметров, либо наоборот, на основе некоторой информации о статистических свойствах параметров требуется определить оптимальный объём выборки или уровень значимости критерия. Для примера рассмотрим решение следующих задач.

Задача 1. Из распределения Коши с плотностью ƒ(x) = 1̸ π[1+(x– a)²] извлечена выборка объёма n; а) будет ли выборочное среднее состоятельной оценкой модыμ_m и/или медианы μ_1/2 этого распределения? б) пусть имеется какая-нибудь состоятельная и несмещённая оценка m медианы (например, выборочная медиана x_1/2); указать нижнюю границу объёма выборки для того, чтобы дисперсия этой оценки не превосходила 0,01.

Решение. Решая уравнение на экстремум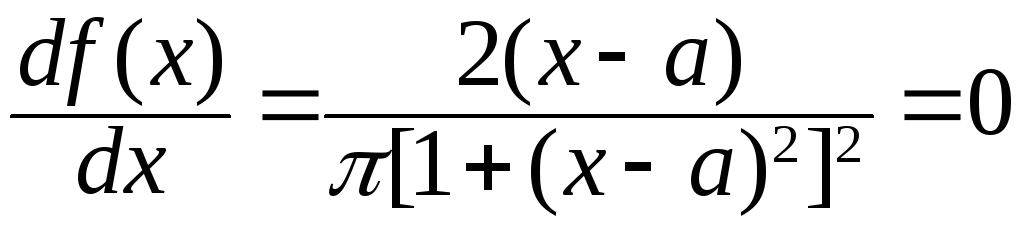находим модальное значениеμ_mo =a..Используя определение медианы рассмотрим интеграл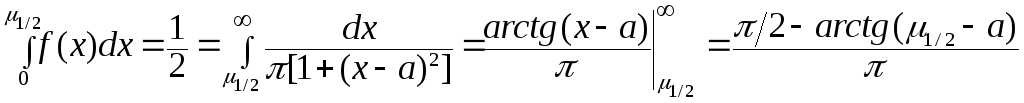, откуда получаемarctg(μ_1/2–a) = 0, то есть медианаμ_1/2=a. Так как медиана и мода для распределения Коши совпадают с параметромположения (сдвига)а, то выборочная оценка для них одна и та же.

Получим выборочную оценку для этого параметра по методу максимального правдоподобия: функция правдоподобия L = 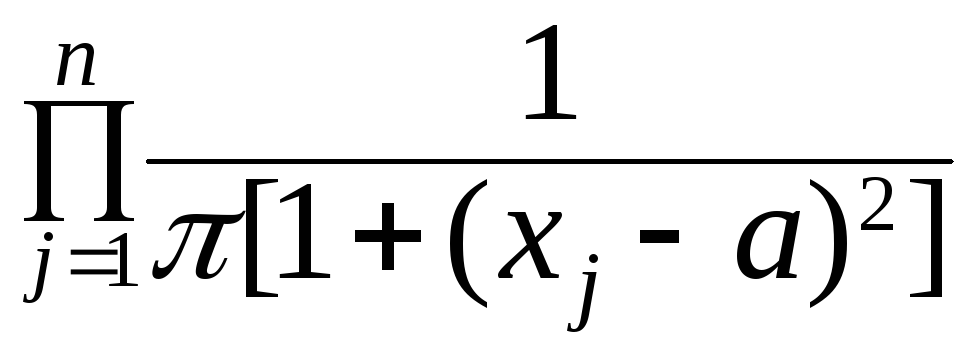; тогда уравнение правдоподобия имеет вид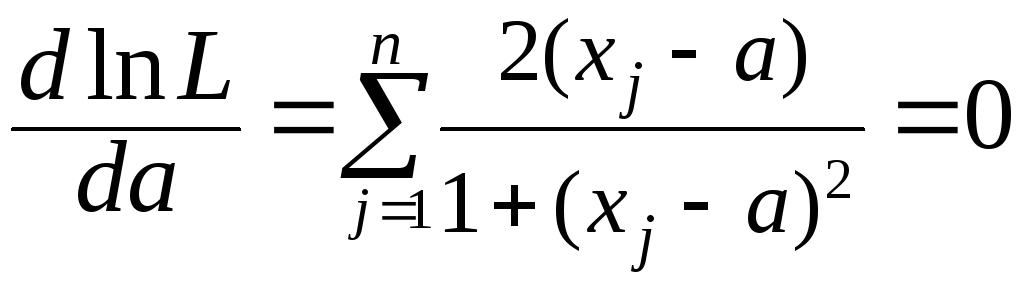, то есть является уравнением степени (2п– 1) по параметруа. Выборочное среднее арифметическое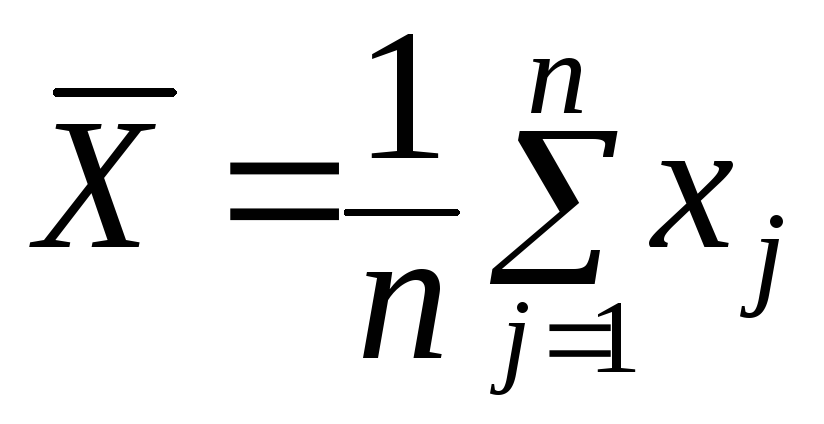в число решений этого уравнения не входит.

а). Состоятельностьоценкиа* параметраа понимается обычно как её сходимость по вероятности к истинному значению параметра:

или .

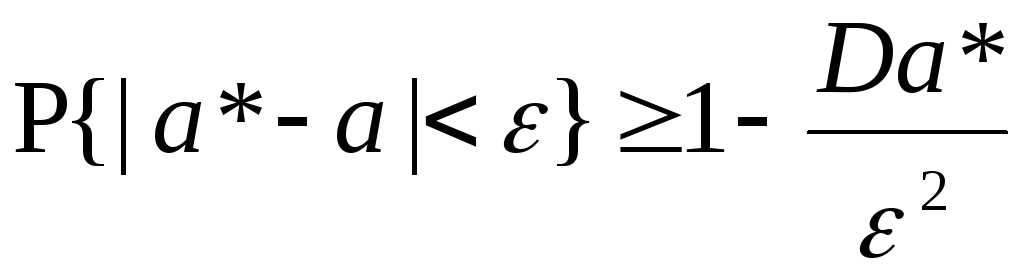Так как выборочное среднее арифметическоеимеет математическое ожидание М= ν₁= μ , т.е. равное первому начальному моменту генеральной совокупности (матожиданию распределения Коши) с одной стороны, а его дисперсияD= μ₂/n = =Dξ/n, гдеDξ– дисперсия генеральной случайной величины (дисперсия распределения Коши). Однако для распределения Коши начальные и центральные моментыне существуют.

Таким образом, выборочное среднее не является состоятельной оценкой медианы (совпадающей в данном случае с модой μ_m)μ_1/2=a.

б). Асимптотическое распределение медианы в окрестности модального значения нормально с дисперсией Dx_1/2=pq / [nf ²(μ_1/2)], где для медианыp = q = ½(формула справедлива для любыхквантилей), а ордината медианы f(μ_1/2) = 1/π. Таким образомDx_1/2=π²/4n. Определим минимальную границу дисперсии (МГД) для распределения Коши: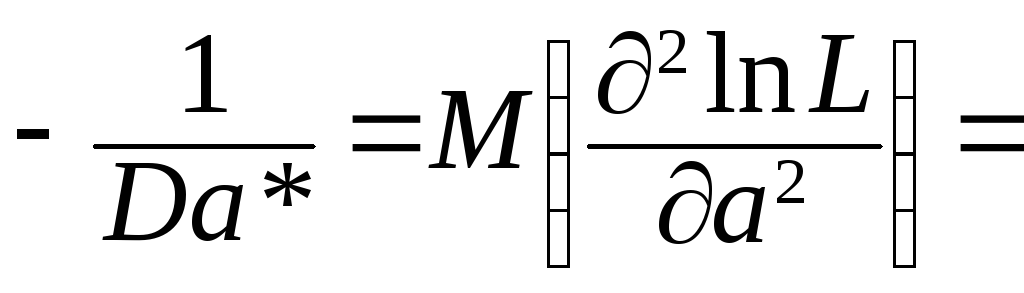

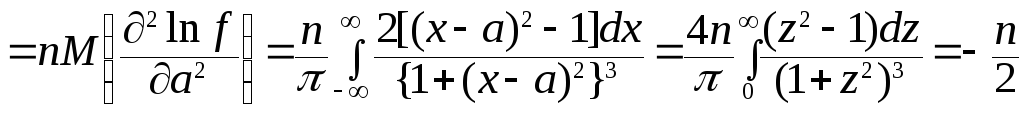. Следовательно, Da* = 2/nдлялюбойоценкиm=a* параметраa распределения Коши (что отличается от дисперсии асимптотического распределения медианы в 8/π²≈ 0,8106). По условию задачи имеем для МГД 2/n≤ 0,01, откудаn ≥ 200.

Задача 2. Сколько нужно получить безотказных срабатываний пожарной сигнализации, чтобы с доверительной вероятностью 0,99 утверждать, что вероятность отказа этой сигнализации не превышает а) 0,001; б) 0,005?

Решение.Здесьn– число опытов, в которых событие (отказ сигнализации) не произошло ни разу, т.е.k= 0. Так как доверительный интервал для вероятностиpв серииnиспытаний Бернулли неё (в случае достаточно большихn, когда значениеpне слишком близко к нулю и единице – условия применимости асимптотики Муавра – Лапласа) определяется соотношениями (3.10), (3.11). Так, соглсно (3.11) верхняя границаp₂для вероятности отказовp, числа опытов n и доверительной вероятности γ связаны соотношенимp₂= 1 –, откуда 1 – γ = (1 –p₂)ⁿ. Логарифмируя последнее уравнение, получаемn = ln(1 –γ)/ln(1 –p₂). По условиюp ≤ p*, γ = 0,99, аp₂= 0,001; 0,005, поэтомуn₁ ≥ ln0,01/ln0,999 ≈ 4606; n₂ ≥ ln0,01/ln0,995 ≈ 922.

УПРАЖНЕНИЕ IV

Указание: Исходные данные и параметры для задач этого упражнения содержатся в таблицах Приложения II.

Задача 1. Пусть выборка A - наблюденные значения случайной величины ξ₁ а такое же число первых элементов выборки B – соответствующие наблюденные значения случайной величины ξ₂. Найти оценку коэффициента ранговой корреляции Кендалла. Аппроксимируя точное распределение нормальным распределением, проверить на уровне значимости (1 - γ) гипотезу Н₀: ρ_с(ξ₁, ξ₂) = 0, против односторонней альтернативы, на которую указывают данные. Каков дости­гаемый уровень значимости?

Решение. Занесём исходные данные в следующую таблицe

A	84	83	83	83	83	81
B	83	83	83	82	82	81
RA	6	3,5	3,5	3,5	3,5	1
RB	5	5	5	2,5	2,5	1

Статистика (коэффициент ранговый корреляции) Кендалла есть величина ρ_с = τ = 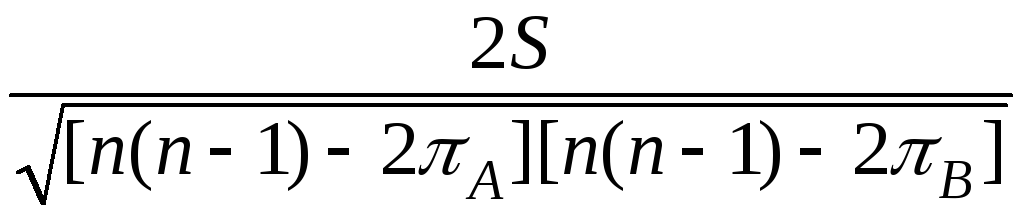, гдеS =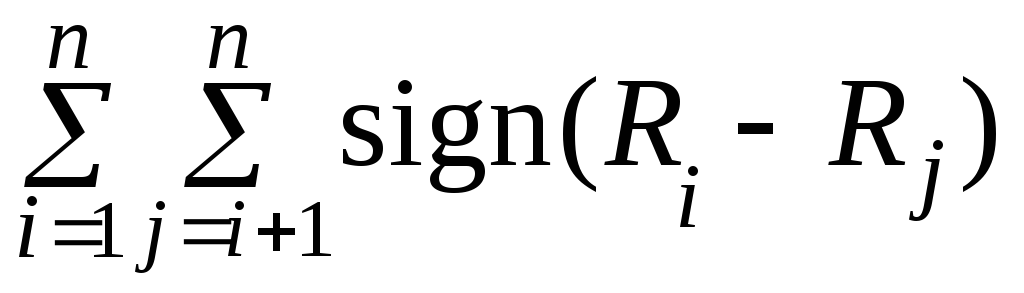; где π_A и π_B – поправки на объединение рангов: π_A (π_B) = 0,5m(m + 1), где суммирование ведётся по группам объединённых рангов; m – число объединённых рангов в каждой группе.

Подставляя исходные данные получаем: π_A = 0,5·4·5 = 10; π_B = 0,5(3·4 + 2·3) = 9; S = + 7 – 4 = 3. Тогда имеем оценку коэффициента ранговый корреляции Кендалла ρ_с = τ ≈ 0,548.

Проверим выполнимость гипотезы H₀: ρ_с = 0 против односторонней альтернативы H₀: ρ_с > 0 при уровне значимости γ =0,8. Так как стандартная ошибка коэффициента ранговой корреляции Кендалла равна σ_c = {2(2n + +5)/[9n(n – 1)]}^1/2 = (34/270)^1/2 ≈ 0,3549, то нулевая гипотеза не отвергается если τ ≤ t_α· σ_c /(n – 1)^1/2. При одностороннем критерии Стьюдента получаем 1 – γ = α/2, то есть по таблице Стьюдента для α = 2(1 – γ) = 2(1 – 0,8) = 0,4 и числа степеней свободы ν = (n – 1) = 5 находим t_0,4 = 0,920. Получаем τ ≈ 0,548≥ 0,146, т.е. полученное значение ранговой корреляции недостоверно.

Практически тот же результат получается при нормальном приближении: 1 – Ф (t_α = τ_α /σ_τ) = α = 2(1 – γ) = 0,4; τ_α /σ_τ = τ_α /0,3549 = 0,254; τ_α = 0,090.

Нулевая гипотеза не выполняется, т.к. τ = 0,548 >>τ_α = 0,090.

Значимость полученного коэффициента корреляции достигается при

t_α ≥ 0,548·(5)^1/2/0,3549 ≈ 3,452,что при данном числе степеней свободы (данном объёме выборок) соответсвует уровню значимости γ ≥ 0,99.

Задача 2.По ранговому критерию Уилкоксона (Манна – Уитни) проверить на уровне значимости (1 - γ) гипотезу однородности выборок A и B при дву­сторонней альтернативе. Каков уровень значимости, рассчитанный по нор­мальной аппроксимации статистики критерия? Исходные данные:

A	84	83	83	83	83	81
B	83	83	83	82	82	81	85	84	86

Решение. Выстраиваем обе выборки в один вариационный ряд в порядке возрастания, присваиваем им ранги двумя способами: один рз по порядку от начала к концу вариационного ряда, а вторично – беря по два элемента и переходя из начала в конец и обратно. Ранги одинаковых вариант при этом усредняются. Представим всё это в виде следующей таблицы:

81	81	82	82	83	83	83	83	83	83	83	84	84	85	86
A	B	B	B	A	A	A	A	B	B	B	A	B	B	B
1,5	1,5	3,5	3,5	8	8	8	8	8	8	8	12,5	12,5	14,5	14/5
2,5	2,5	6,5	6,5	12	12	12	12	12	12	12	6,5	6,5	3	2

Подсчитаем сумму рангов по обеим ранжировкам для элементов выборок A иB: U_1,A= 46; U_1,B= 84; U_2,A= 57; U_2,B= 63.

Нулевая гипотеза H₀состоит в данном случае в том, что обе выборки представляют одну и туже генеральную совокупность. В предположении выполненности гипотезыH₀статистика U(m,n) критерия Вилкоксона бысро схолится к нормальному с математическим ожиданиемµ_U=n·( n + m + 1) / 2 и дисперсиейD_U=σ_U²=m·n·(n + m + 1) / 12, гдеn и m –объёмы выборок. В данном случаеµ_U= 54;D_U= 99;σ_U= 9,950.

Нулевую гипотезу об однородности двух выборок предлагается разделить на две гипотезы: гипотеза о равенстве средних(H₀:µ_A=µ_B) игипотеза о равенстве дисперсий (H₀:D_A=D_B). Для обеих гипотез границы критической области определяются соотношением:

P{|_Un,m –µ_U| >u_{α /2}(n,m)} = 1 – Ф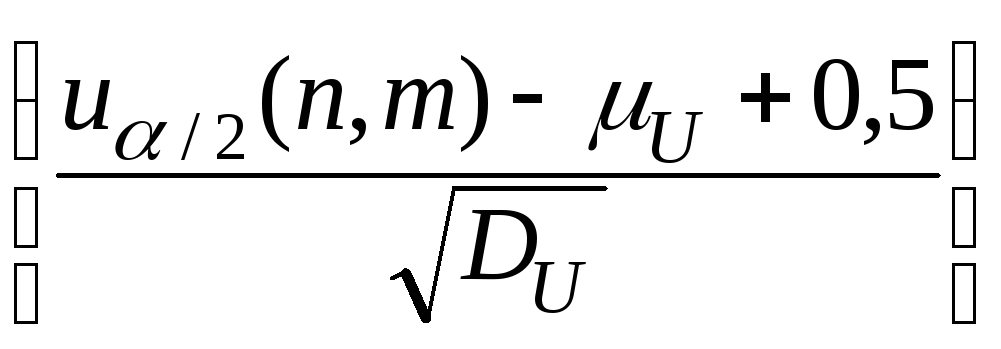=α/2.

Замечание: Добавка 0,5 в числителе аргумента функции Лапласа – это поправка Шепарда на дискретность, что существенная при выборках малого объёма.

Для заданному по исходным данным уровню доверия γ = 0,8 определяем критерий значимости α= 1 – γ = 0,2; тогда Ф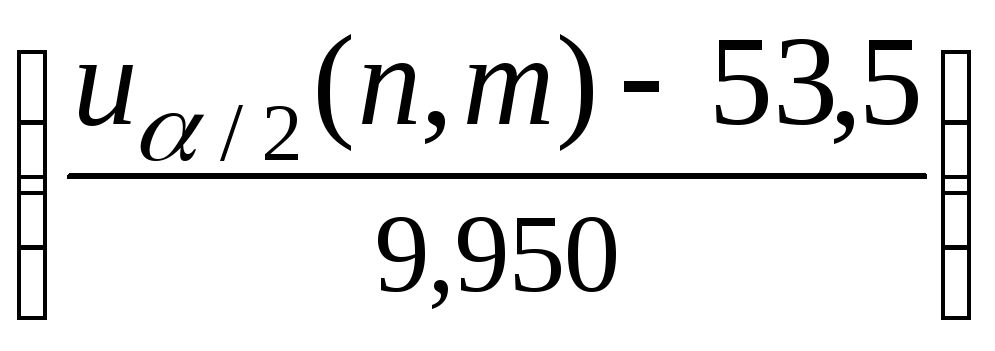= 0,9 и по таблицам нормального распределения находимu_{α /2}(n,m) = 53,5 + 9,95·1,282 = 53,5 + 17,559 = 71 (берём целую часть). Запишем теперьинтервал принятия нулевых гипотез: [7, 61]. Так как выборочные статистики равны:U_1,A = 46 U_2,B = 57 и обе попадают в этот интервал, то нулевая гипотеза об одородности заданных выборок не может быть отвергнута.

УПРАЖНЕНИЕ V

Используя в качестве исходных данных корреляционную таблицу вашего варианта (ПриложениеIII) необходимо: 1) определитьточечные выборочные оценки:коэффициента корреляции Пирсона ρ,коэффициентовобеихлинейных регрессий α₁, α₂, β₁, β₂;корреляционных отношений η₁² и η₂² случайных величин ξ₁ и ξ₂; 2) рассчитатьдоверительные интервалыдля указанных величин; 3)найти оценку линейных функций регрессии с 95% доверительным интервалом для пред­сказаний и построить их график; 4)проверить на уровне значимости (1 - γ) = 0,05 гипотезыналичия/отсутствия (Н₀: ρ = 0 противгипотезы Н₁: ρ ≠ 0) илинейности/нелинейности(гипотеза Н₀: ρ² = η₁² = η₂² = 0 против гипотезы Н₁: регрессия может быть любой формы) корреляции.

Решение. Дан закон распределения двумерной случайной величины (ξ₁, ξ₂) в виде таблицы:

Y|X	10	15	20	25	30	35
50	0,01	0,02	0,01
60	0,02	0,04	0,05	0,06	0,04
70		0,02	0,05	0,2	0,1	0,04
80			0,02	0,1	0,1	0,06
90					0,02	0,04

где X и Y – множества значений случайных величин ξ₁ и ξ ₂, соответственно. Воспользуемся результатами решения задачи 8 ИДЗ 2 части I «Практикума по теории вероятностей.

Преобразуем заданную корреляционную таблицу следующим образом:

1) Вероятности маргинальных распределений инайдём по формулам:и, суммируя элементы таблицы по столбцам и строкам, соответственно; результаты запишем в дополнительной нижней строке – она будет задавать нам маргинальное распределение случайной величиныξ₁, и в дополнительном правом столбце – вероятности маргинального распределения случайной величины ξ₂. Кроме того, в клетках таблицы с ненулевами вероятностями запишем в левом верхнем углу значения соответствующих произведенийxy. Таблица примет следующий вид:

Y|X	10	15	20	25	30	35
50	500 0,01	750 0,02	1000 0,01				0,04
60	600 0,02	900 0,04	1200 0,05	1500 0,06	1800 0,04		0,21
70		1050 0,02	1400 0,05	1750 0,2	2100 0,1	2450 0,04	0,41
80			1600 0,02	2000 0,1	2400 0,1	2800 0,06	0,28
90					2700 0,02	3150 0,04	0,08
	0,03	0,08	0,13	0,36	0,26	0,14

2) Вычислим математические ожидания Мξ₁ = μ₁ ; Мξ₂= μ₂ и средние квадратические отклонения σ₁ ; σ₂ этих величин:

Мξ₁ = μ₁==10·0,03+15·0,08+20·0,13+25·0,36+30·0,26+35·0,14 =25,8;

Мξ₂ = μ₂== 50·0,04+60·0,21+70·0,41+80·0,28+90·0,06 =71,1;

σ₁ = ==(100·0,03 + 225·0,08 + 400·0,13 + 625·0,36 + 900·0,26 + +1225·0,14 – (25,8)²)^½ = 6,15;

σ₂===

–(71,1)²)^1/2 = 9,37.

3) Запишем, оформив их в виде таблиц, условные законы распределения ξ₁ (при условии ξ₂ = y_j) и ξ₂ (при условии ξ₁ = x_k), называемые также регрессиями ξ₁ по ξ₂ и ξ₂ по ξ₁, соответственно. При этом используем соотношения:

; в последних столбцах таблиц запишем значения условных математических ожиданий M(ξ₁ | ξ₂ = y_j) = M(ξ₁ | y_j) =

и М (η | ξ = x_k) = М (η |x_k) = :

X	10	15	20	25	30	35	= =
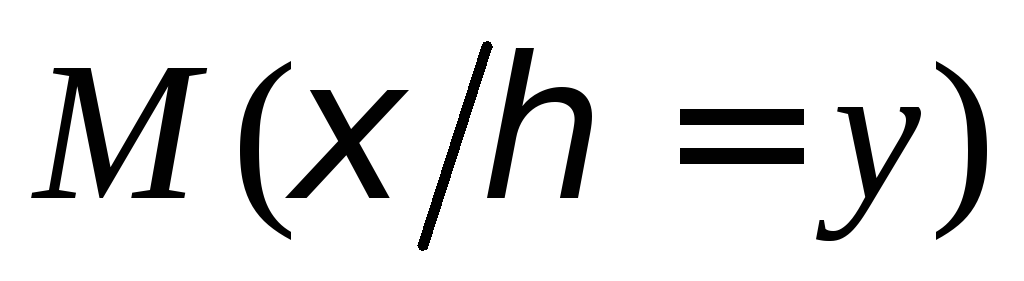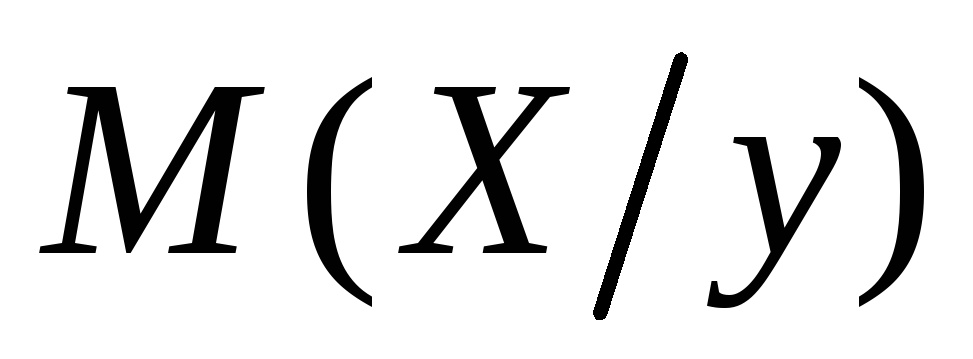
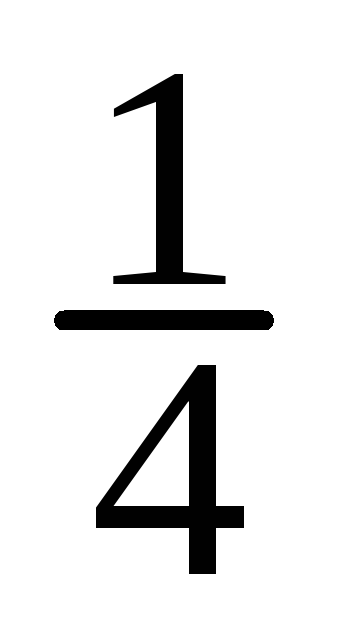
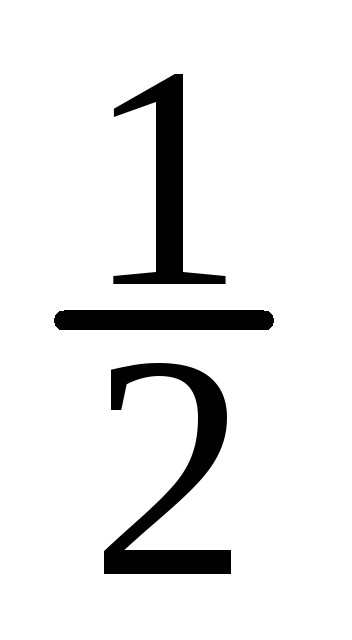
							15

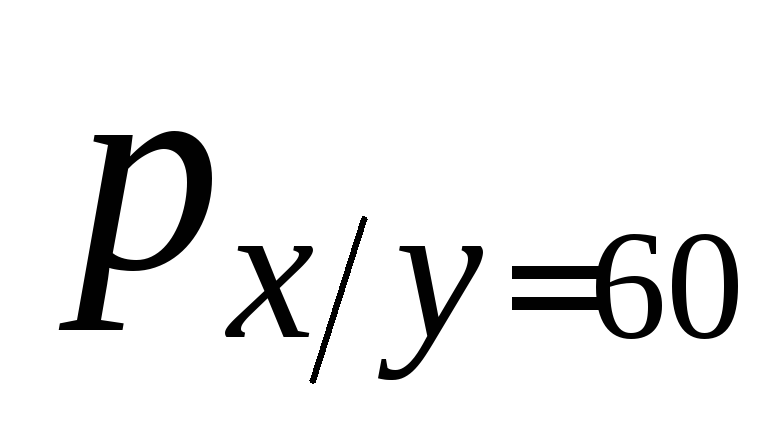
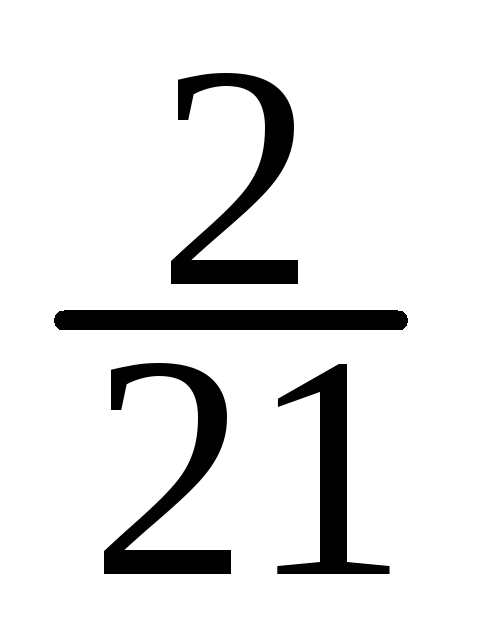
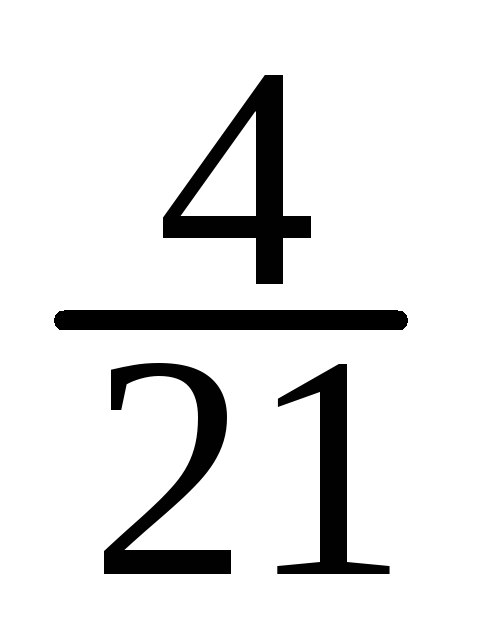
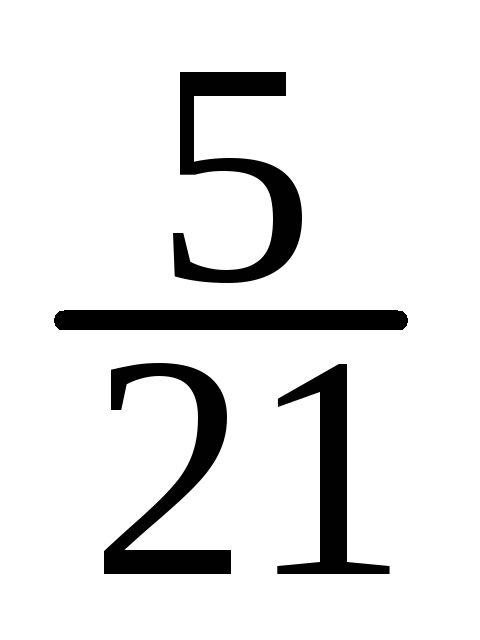
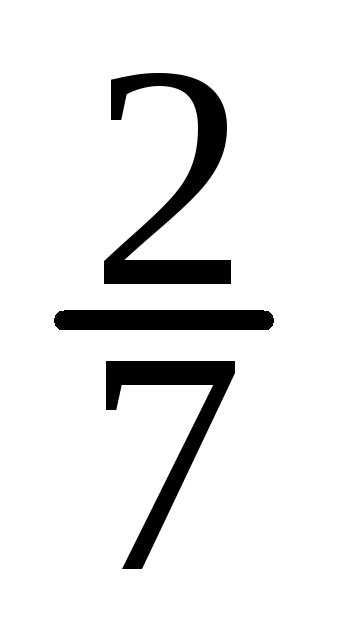
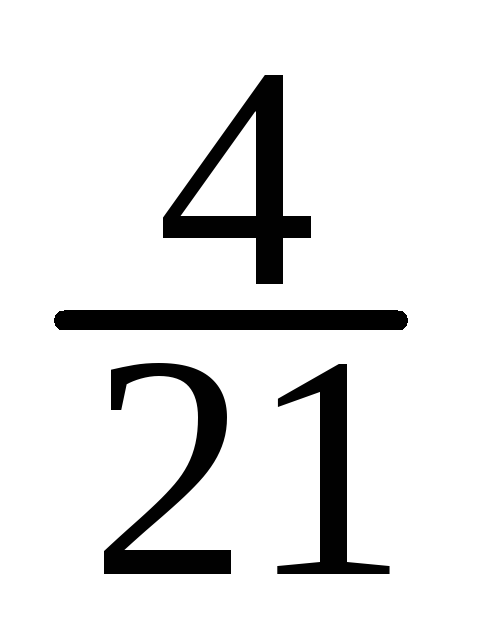
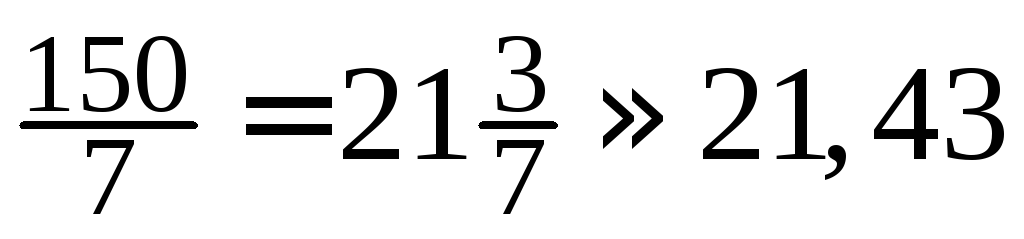
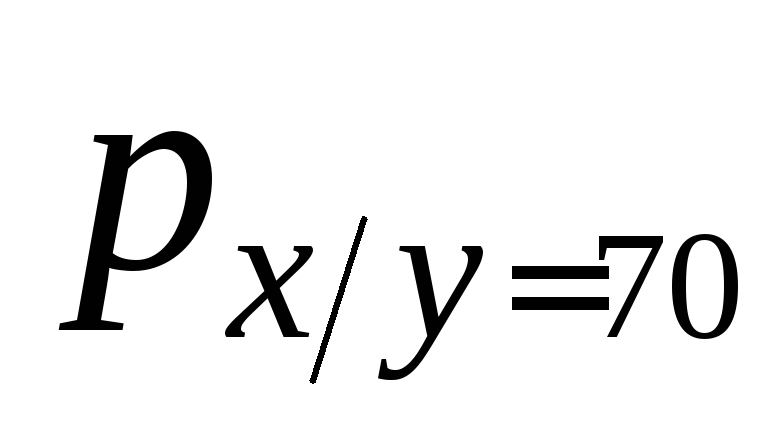
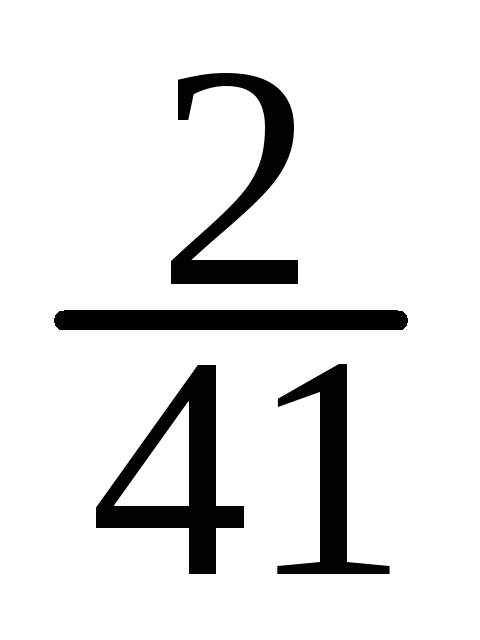
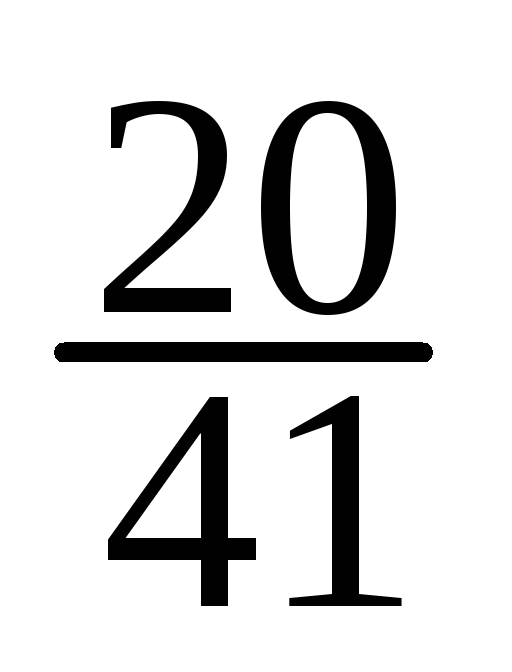
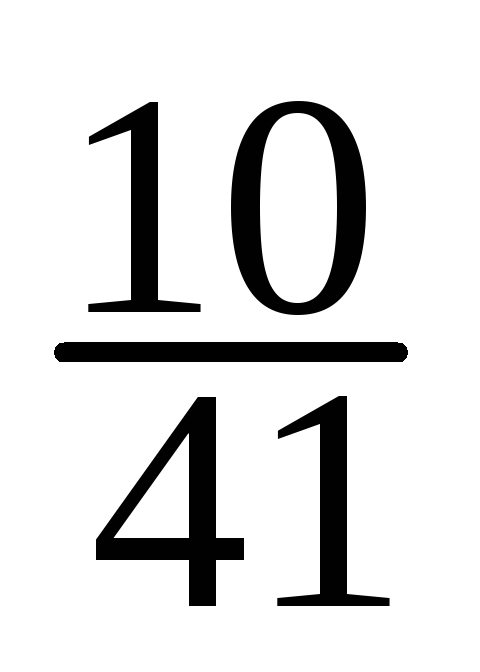
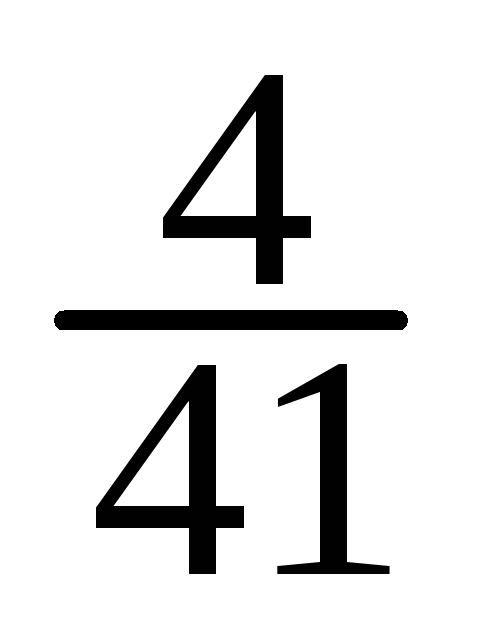
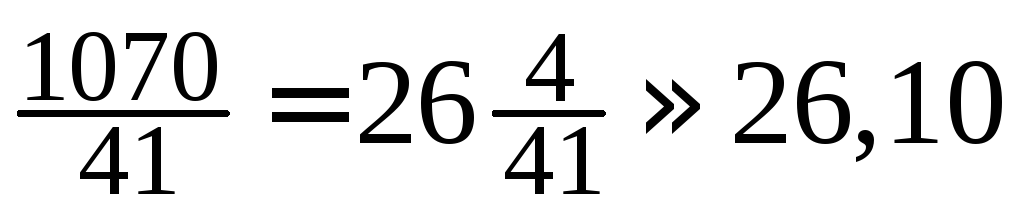
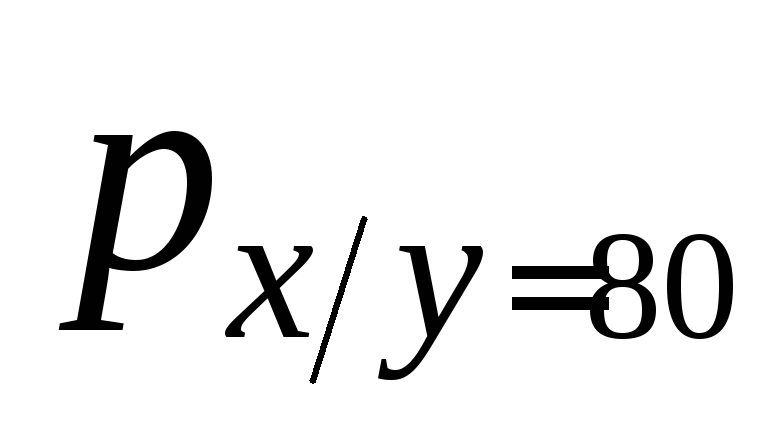
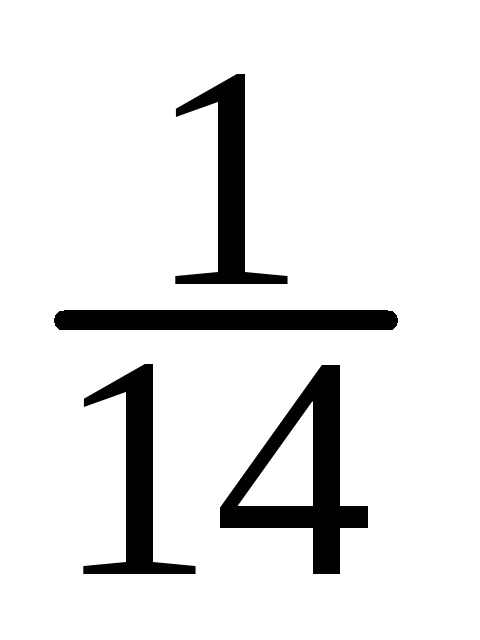
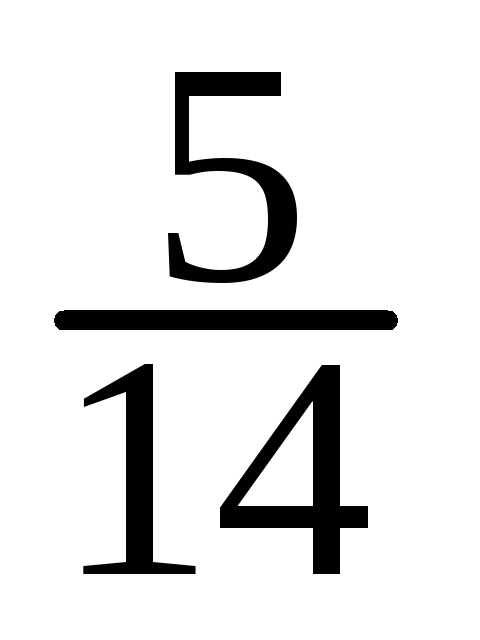
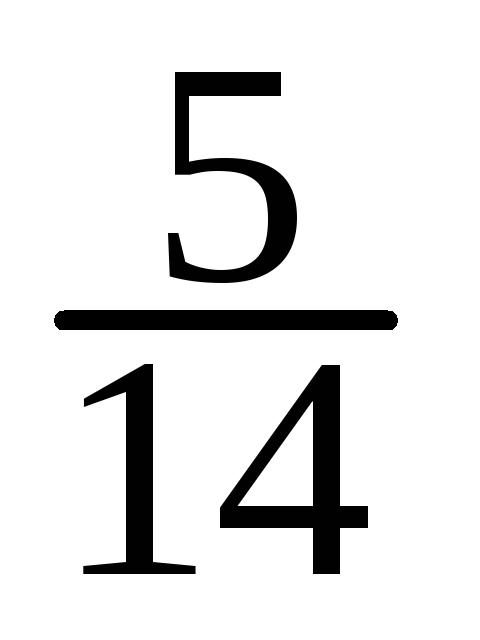
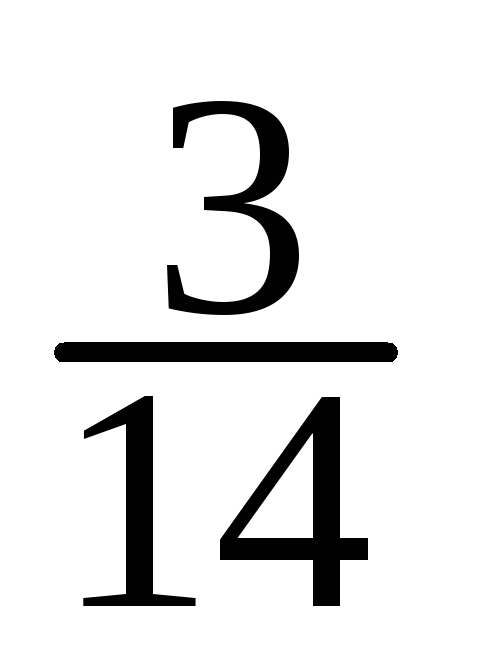
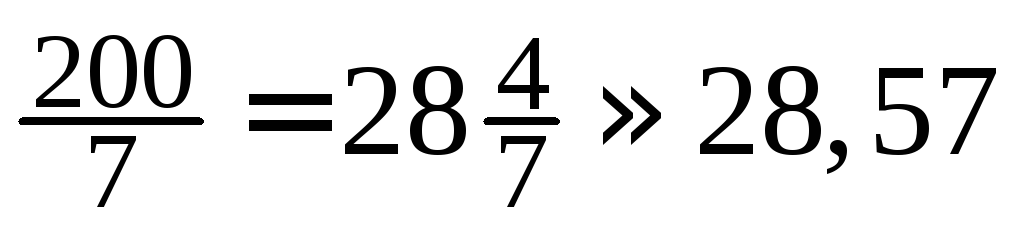
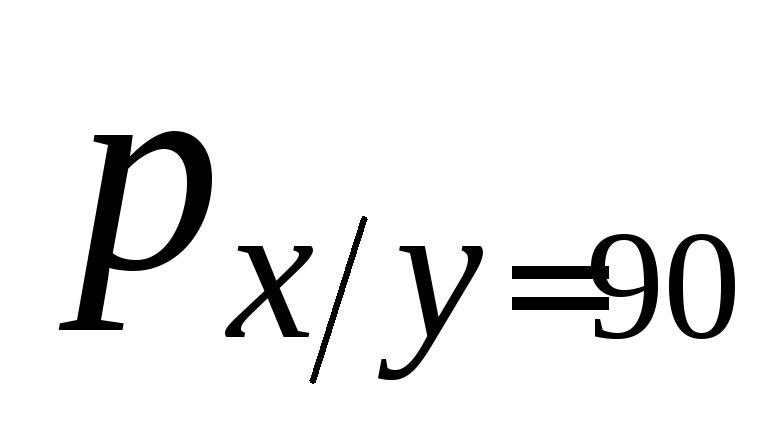
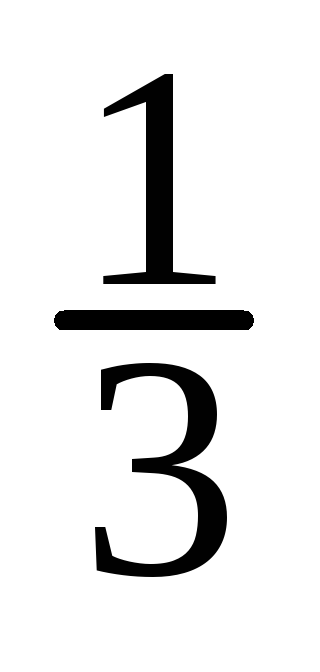
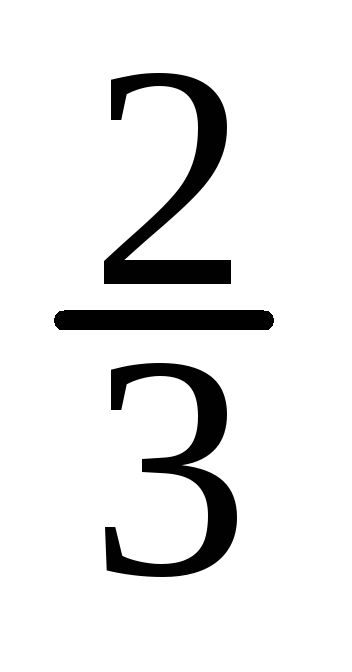
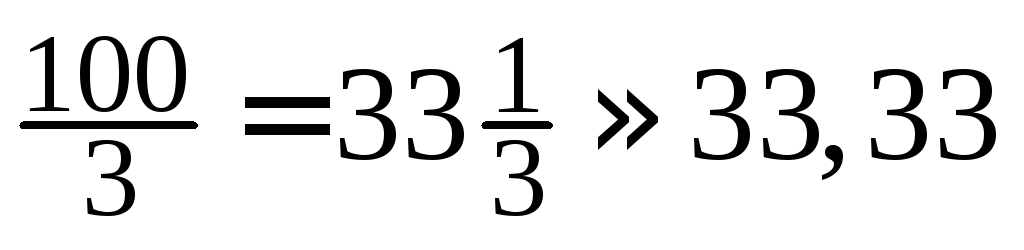
Y	50	60	70	80	90	= =
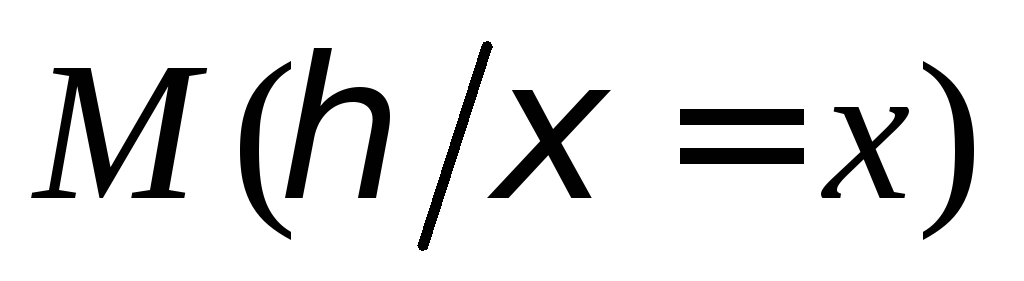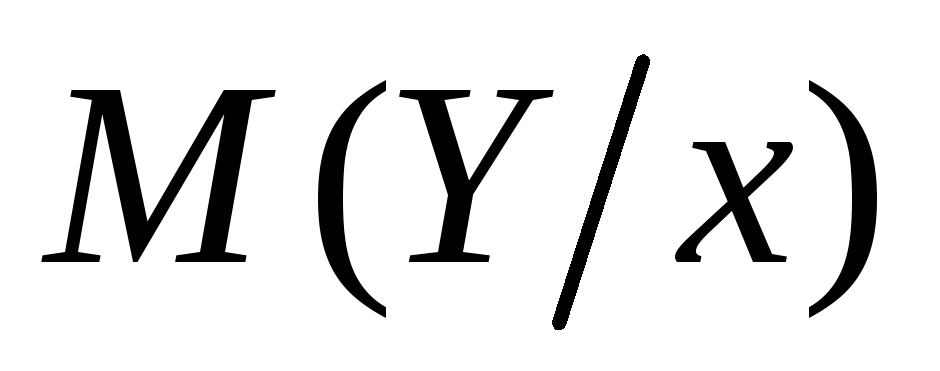
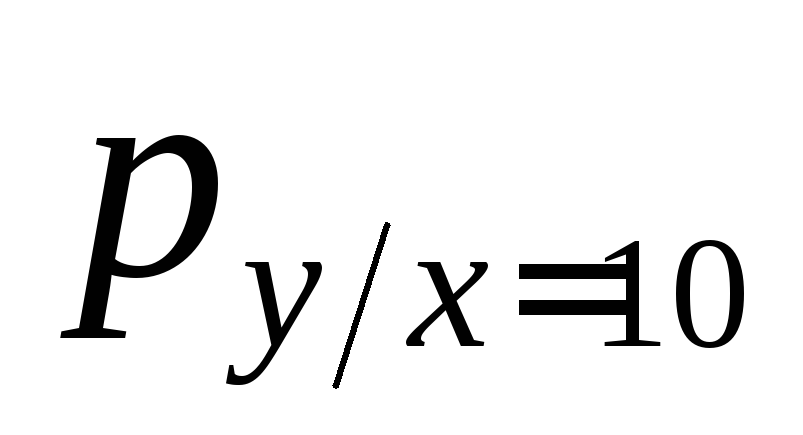
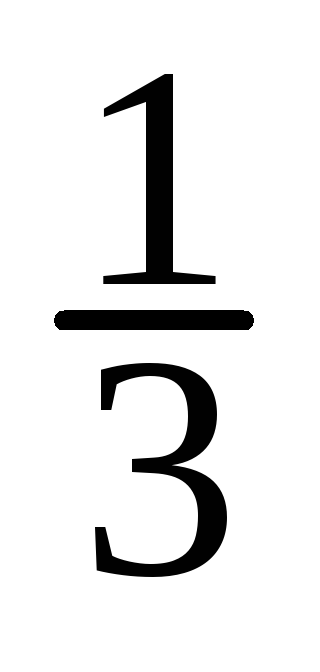
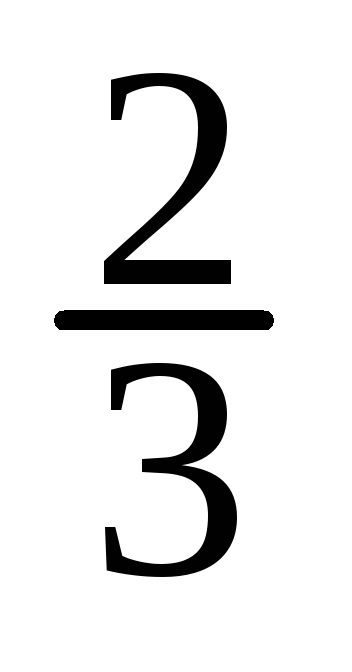
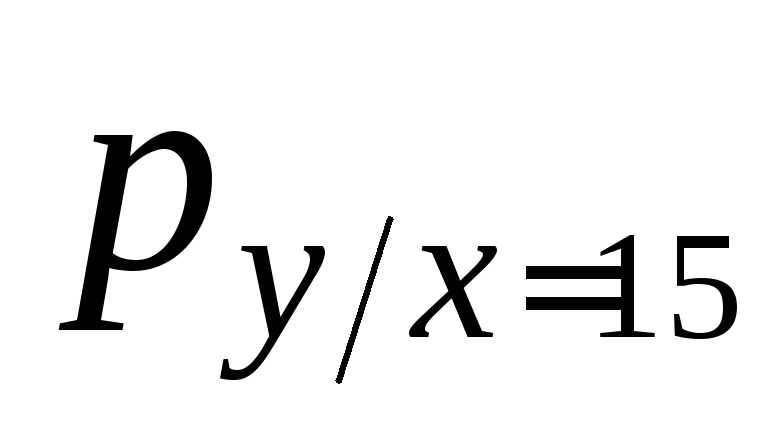
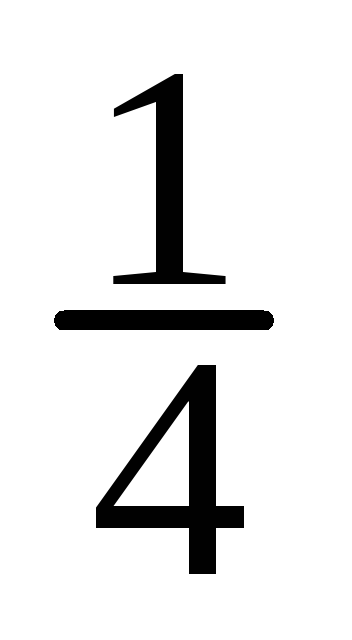
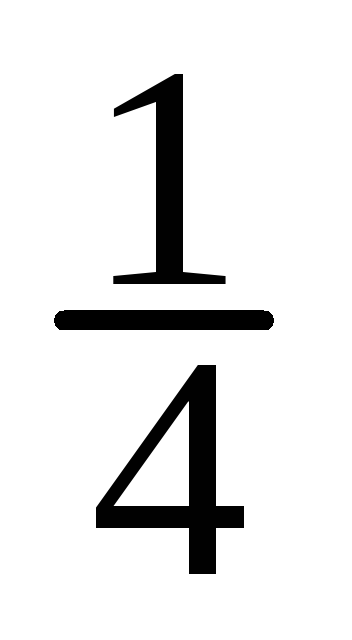
						60

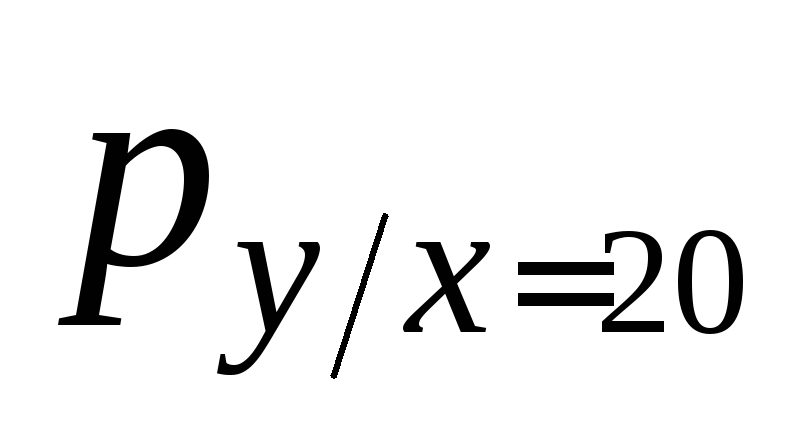
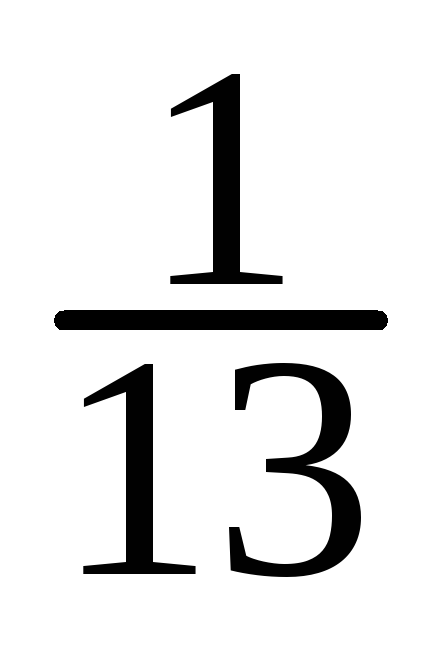
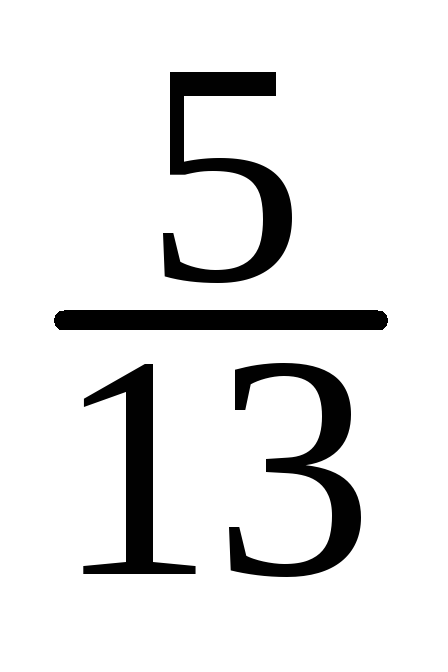
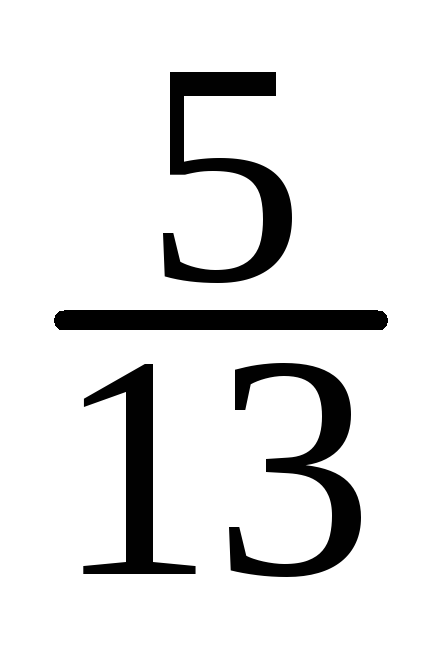
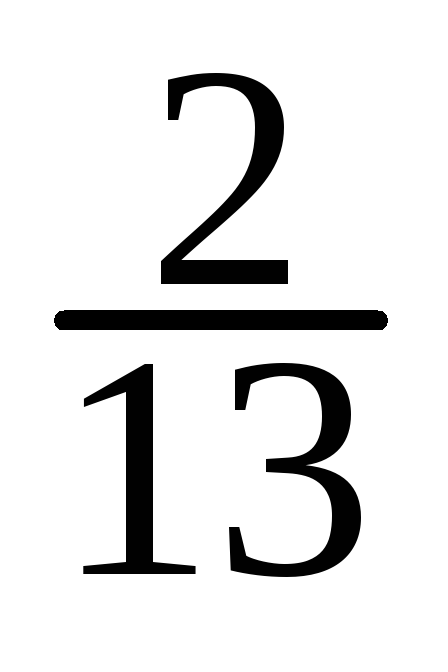
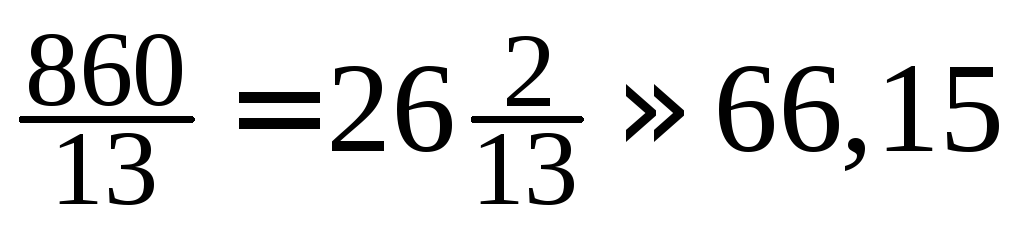
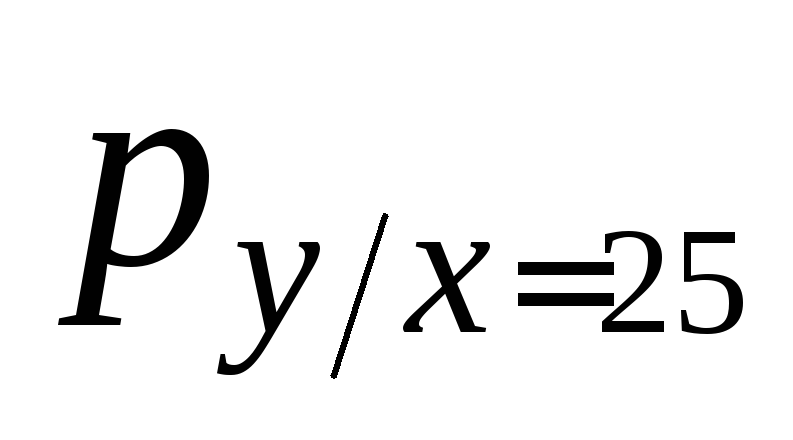
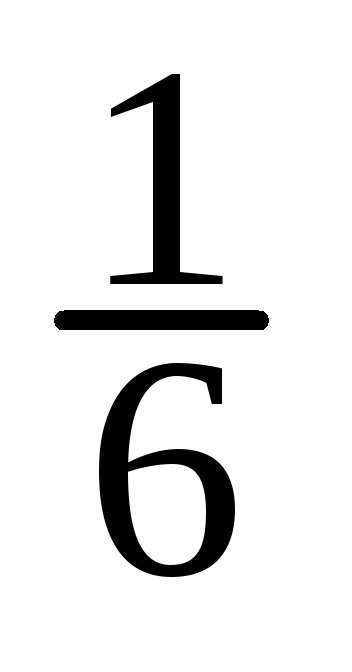
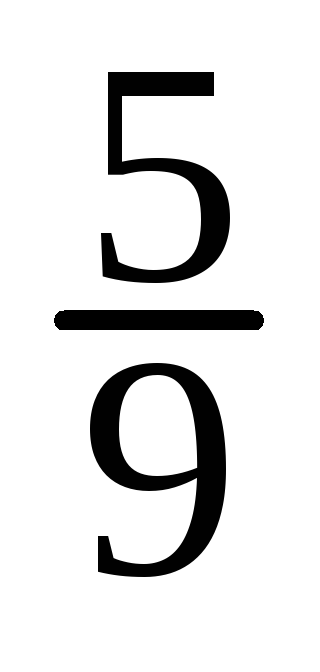
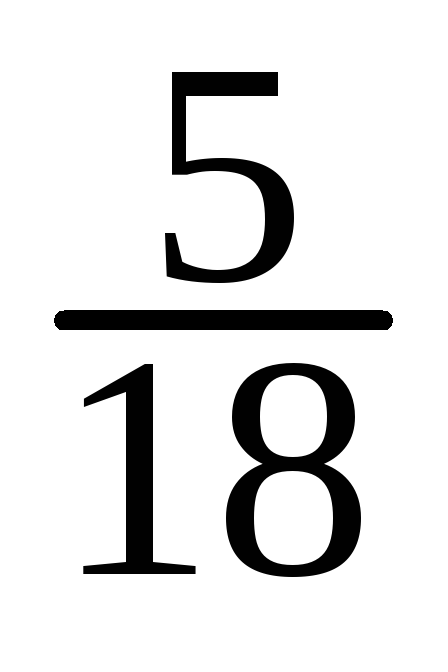
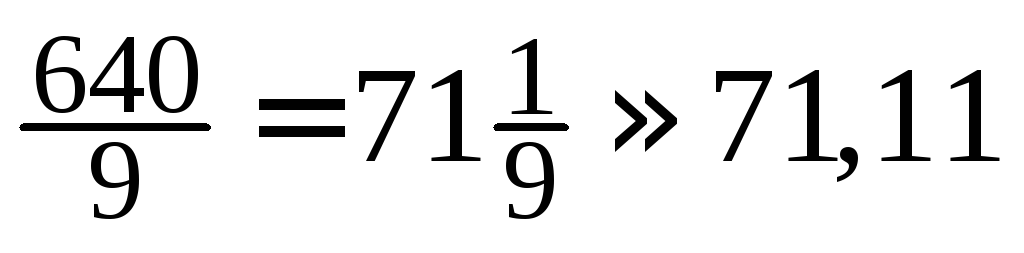
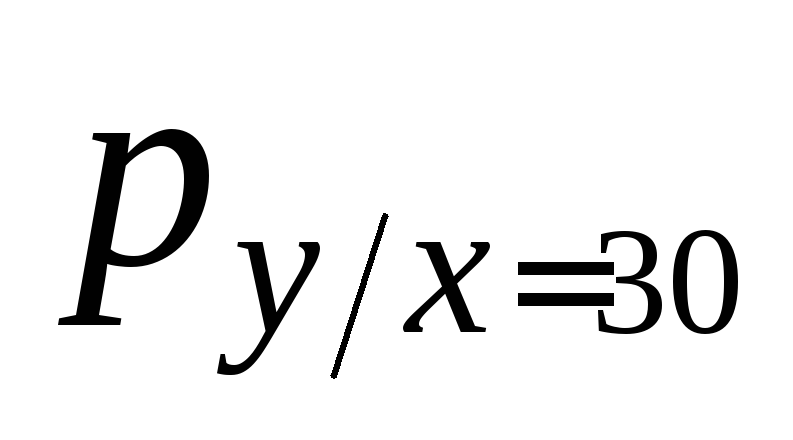
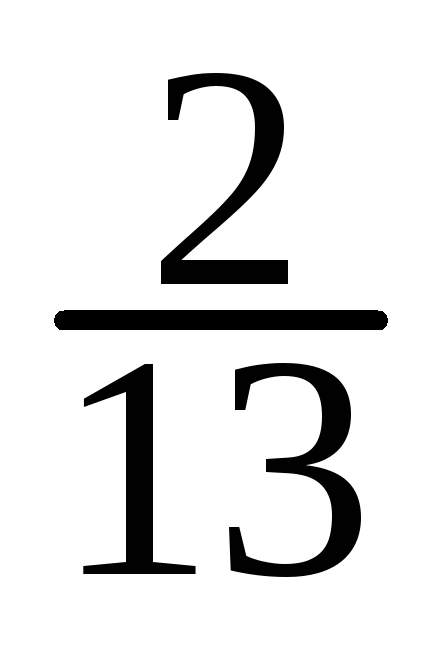
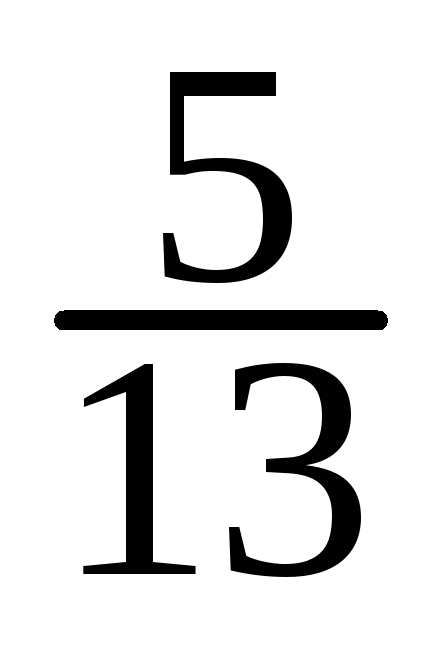
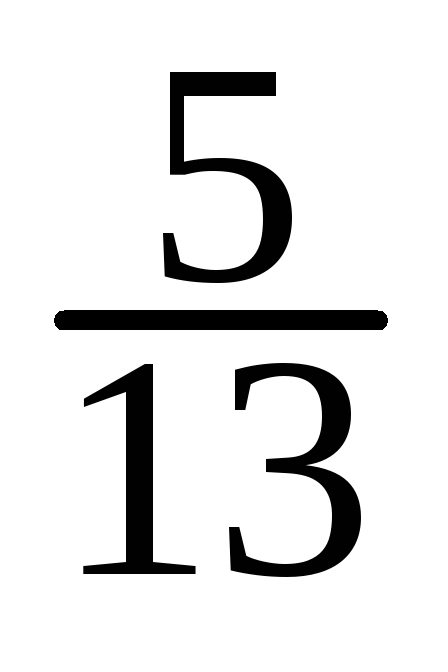
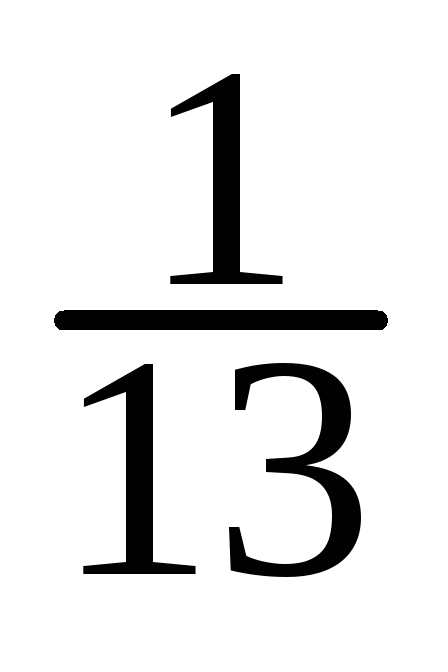
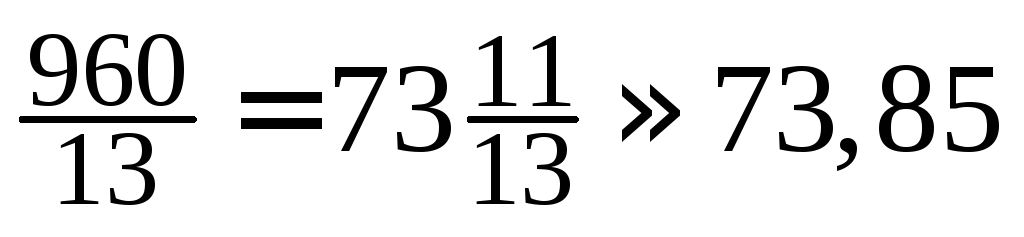
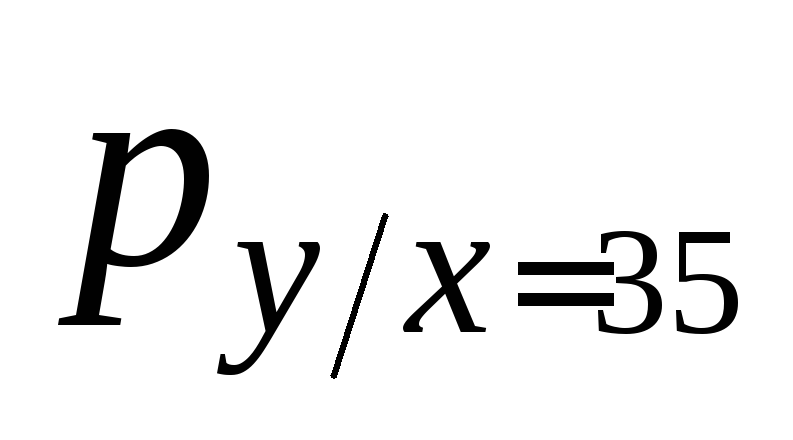
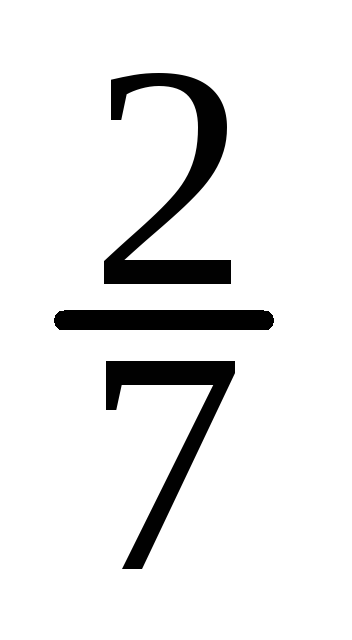
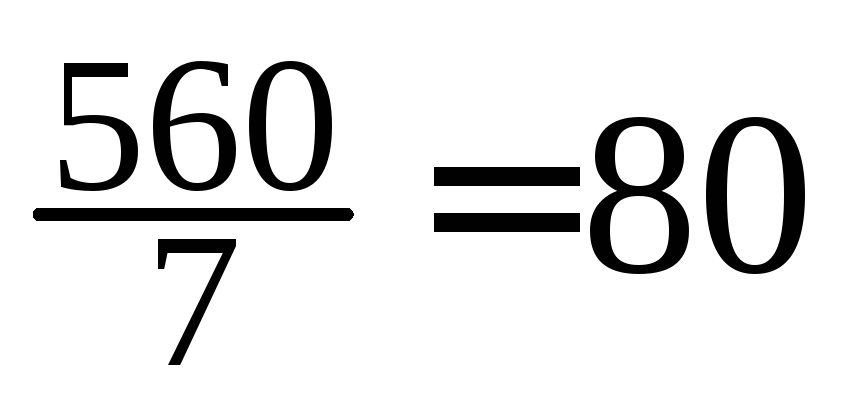
4) Находим ковариацию cov (ξ, η) = μ*₁₁, оценки b₁ и b₂, a₁ и a₂ коэффициентов регрессии β₁, β₂ и выборочный коэффициент корреляции r(ξ, η):

cov (ξ, η) = μ₁₁ = ==

= 500·0,01+ 600·0,02 + 750·0,02 + 900·0,04 + 1050·0,02 + 1000·0,01 + 1200·0,05 + 1400·0,05 + 1600·0,02 + 1500·0,06 + 1750·0,2 + 2000·0,1 + 1800·0,04 +

+ 2100·0,1 + 2400·0,1 + 2700·0,02 + 2450·0,04 + 2800·0,06 + 3150·0,04 –

– 25,8·71,1 = 1851 – 1834,38 = 16,62;

r(ξ₁, ξ₂) =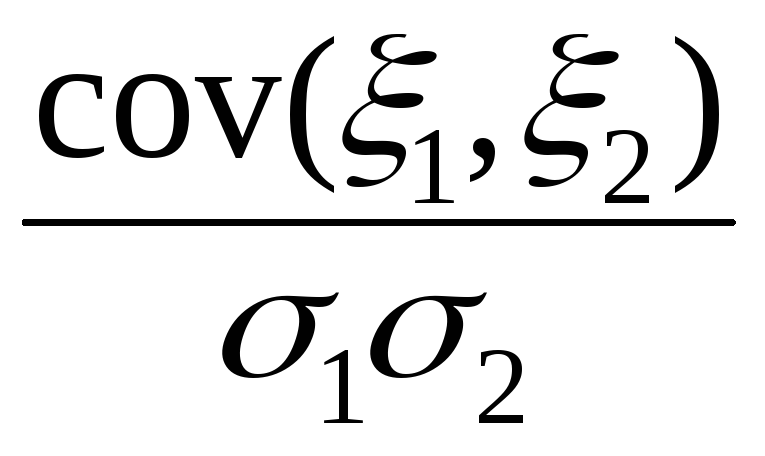==0,29; b₁ = = 0,29·=0,19;

b₂ = = 0,29·=0,44; a₁ ==25,8 – 0,19·71,1=12,301;

a₂ = = 71,1 – 0,44·25,8 = 59,748.

5) Уравнения прямых регрессий имеют вид: , то естьy – 71,1 = 0,44·(x – 25,8); x – 25,8 = 0,19· (y – 71,1) или y = 0,44x + 59,75; x = 0,19y + 12,29.

6) Изобразим значения условных математических ожиданий и прямые регрессии в координатах (ξ₁, ξ₂):

ξ₂

90 * ξ₁ по ξ₂

80 * * ξ₂ по ξ₁

71,1 *

70 * *

*

60 * *

*

50 *

25,8 ξ₁

10 15 20 25 30 35

Комментарий 5.1. Полученные результаты позволяют предположить, что либо стохастическая свзь между ξ₁ и ξ₂ слабая (при условии её линейности), либо эта связь нелинейна. Для более точного ответа на зти вопросы, необходимо проверить соответствующие статистические гипотезы. Но предварительно следует оценить надёжность полученных результатов.

Доверительные интервалы для полученных коэффициентов корреляции и регрессии имеют вид: a_i – t_q·S(α_i) ≤ α_i ≤ a_i + t_q·S(α_i); b_i – t_q·S(b_i) ≤ β _i ≤ b_i + t_q·S(b_i); i = 1, 2. Величины t_q определяются по таблицам P{t > t_q} = q =

=(1 - γ)/2 распределения Стьюдента (Приложение IV) для ν = n – 2 степеней свободы. Доверительный интервал для коэффициента корреляции имеет вид r(ξ₁, ξ₂) – t_γ·S(r) ≤ ρ(ξ₁, ξ₂) ≤ r(ξ₁, ξ₂)+ t_γ·S(r), если полагать, что n достаточно велико, чтобы считать нормальную асимптотику распределения коэффициента корреляции справедливой. Вполне достаточно, если n ≥ 400. В нашем случае n = 100, что также не мало, но может оказаться недостаточно, если требования к точности оценок достаточно высоки. Поэтому проведём также контрольную оценку через Z-переменную Фишера, которая нормальна уже при n ≥ 20. В этом случае доверительный интервал имеет вид: r₁ < ρ < r₂, где

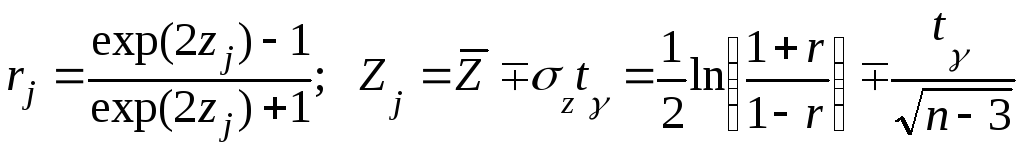, где верхний знак соответствует j = 1, нижний – j =2. Величина t_γ определяется по таблице функции Лапласа как корень уравнения P{t < t_γ} = Φ(t_γ) = (1 + γ)/2. Используя данные и полученные величины, находим:

S²(α_i) =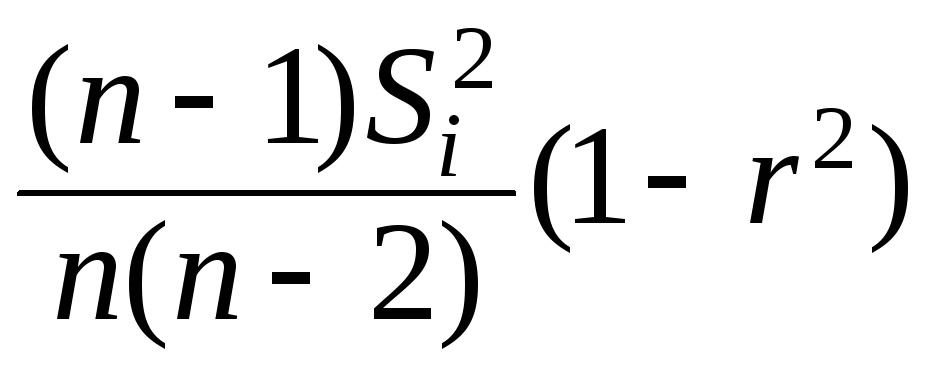;i = 1, 2; S²(α₁) = (99·6,15·0,9159)/(100·98) = 0,0569;

S(a₁) = 0,24; S²(α₂) = (99·9,37·0,9159)/(100·98) = 0,0867; S(α₂) = 0,29;

S²(b₁) = 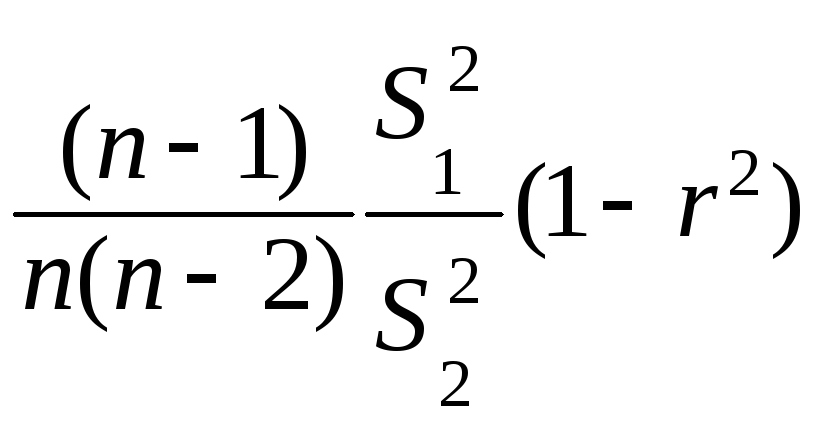= (99·6,15·0,9159)/(100·98·9,37) = 0,0061; S(b₁) = 0,0775 ≈ 0,08; S²(b₂) = 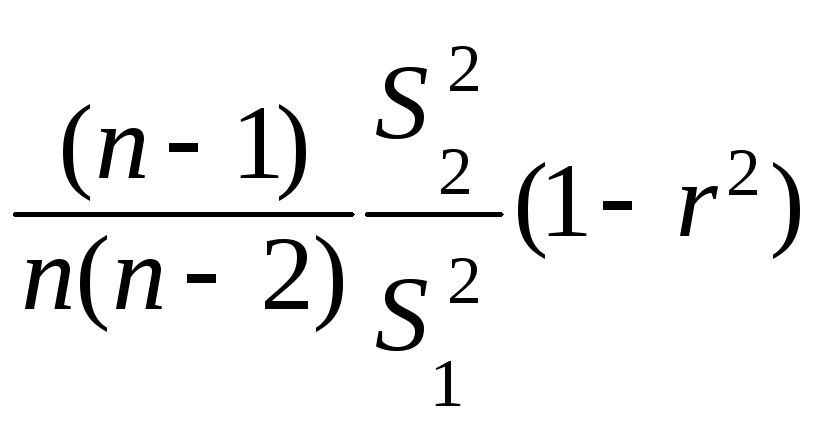= 0.0867/6,15 = 0,0141; S(b₂) = 0,119 ≈ 0,12; S²(r) == [1 – (0,29)²]/100 = 0.9159/100 = 0,0092; S(r) = 0,0959 ≈0,10.

Для γ = 0,95 и γ = 0,99 находим с помощью таблиц Приложений: так как q =

(1– γ)/2 = 0,025 в первом и 0,005 во втором случаях, то по таблице Стьюдента находим t_0,025 = 1,984 и t_0,005 = 2,626. Для величины t_γ имеем (1 + γ)/2 = 0,975 при γ = 0,95 и 0,995 при γ = 0,99; по таблице функции Лапласа находим: t_0,975 = 1,960; t_0,995 = 2,575. Расчёты дают также: Z_{1; 0,95} = 0,038; Z_{2; 0,95} = 0,560;

Z_{1; 0,99} = 0,100; Z_{2; 0,99} = 0,497; exp(2Z_{1; 0,95}) = 1,079; exp(2Z_{2; 0,95}) = 3,065; exp(2Z_{1; 0,99}) = 1,221; exp(2Z_{2; 0,99}) = 2,702.

В результате получаем следующие доверительные интервалы:

при уровне доверия γ = 0,95: 11,82 ≤ α₁ ≤ 12,58; 59,17 ≤ α₂ ≤ 60,33;

0,04 ≤ β₁ ≤ 0,34; 0,20 ≤ β₂ ≤ 0,68; 0,042 ≤ ρ(ξ₁, ξ₂) ≤ 0,538; 0,038 ≤ ρ ≤ 0,508;

при уровне доверия γ = 0,99: 11,67 ≤ α₁ ≤ 12,93; 58,98 ≤ α₂ ≤ 60,51;

- 0,03 ≤ β₁ ≤ 0,40; 0,12 ≤ β₂ ≤ 0,76; 0,102 ≤ ρ(ξ₁, ξ₂) ≤ 0,378; 0,100 ≤ ρ ≤ 0,460.

Комментарий 5.2. Сравнение доверительных интервалов интервалов для коэффициента корреляции, полученных как в предположении его нормального распределения, так и с помощью практически нормальной статистики Z, показывает сопоставимость результатов. Это позволяет, с одной стороны, говорить о достаточности объёма выборки n = 100 для применения нормальной аппроксимации распределения выборочного коэффициента корреляции, а с другой стороны, а точнее одновременно, можно сделать предположение о распределении исходных данных, близком к двухмерному нормальному.

Далее исследуем полученную корреляцию на значимость и линейность. Проверим гипотезу H₀: ρ = 0 против простой альтернативы H₁: ρ > 0. Нулевую гипотезу принимаем , если выборочная статистика t_n < t_α. Величина

t_n = 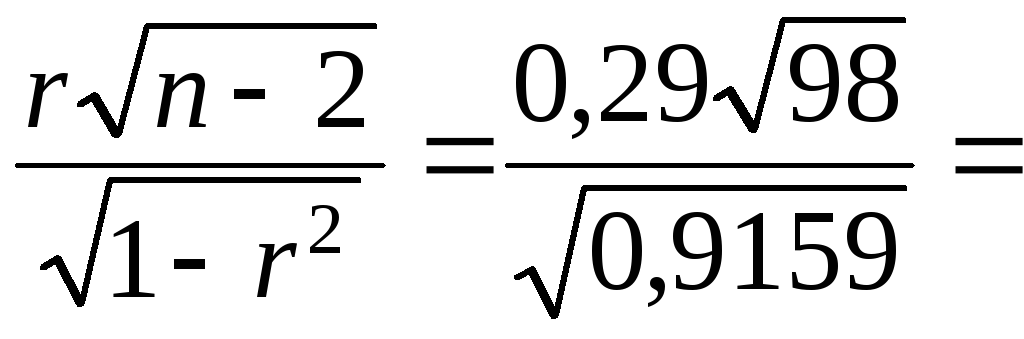0,273; величина t_α выбирается по таблице Стьюдента как решение уравнения P{t > t_α} = α = 1 – γ с n – 2 степенями свободы. Для γ = 0,95 находим t_0,05 = 1,660, а для γ = 0,99 находим t_0,01 = 2,364. В обоих случаях нулевая гипотеза принимается.

Комментарий 5.3. Полученный результат означае лишь, что значение выборочного коэффициента корреляции незначимо; статистической зависимости либо действительно нет, либо она существенно нелинейна.

Для проверки гипотезы нелинейности корредяции вычислим выборочные корреляционные отношения (6.33) и (6.34):

выборочное корреляционное отношение ξ₁ по ξ₂ 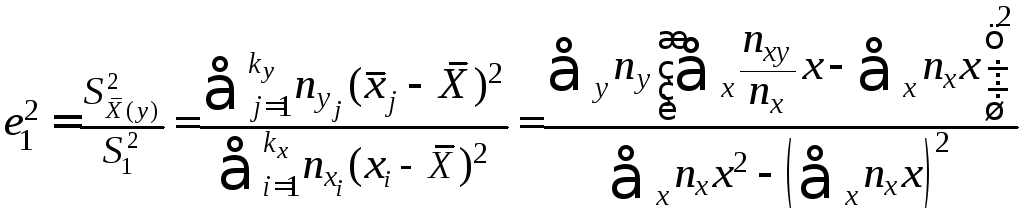=0,3669;

и выборочное корреляционное отношение ξ₂ по ξ₁

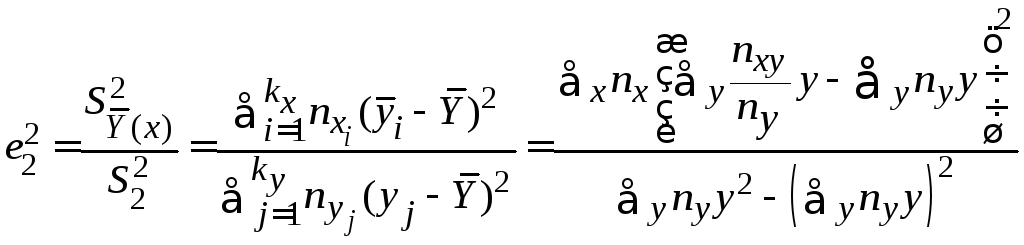= 0,3684.

Для проверки гипотезы H₀: регрессия ξ₁ по ξ₂ линейна пртив альтернативы H₁: регрессия ξ₁ по ξ₂ может быть любой форм,ы кроме линейной (аналогично для регрессии ξ₂ по ξ₁) рассчитаем статистики ,k_i - количества X- иY-сечений, соответственно. В данном случае k₁ = 5; k₂ = 6. Соответственно получаем статистики F_{99, 95} = [(0,3669 – 0,0841)/3]/[(1 – 0,3669)/95] = 14,150; F_{99, 94} = [(0,3684 – 0,0841)/4]/[(1 – 0,3684)/94] = 10,557, которые подчиняются распределению Фишера с соответствующими числами степеней свободы. По таблицам этого распределения, при заданных уровнях доверия, находим критические значения: при γ = 0,95 F_{99, 95}^(кр.) = 1,40; при γ = 0,99 F_{99, 94}^(кр.) = 1,62. В обоих случаях расчётные статистики значительно превышают критические значения, т.е. нулевая гипотеза отвергается; обе регрессии существенно нелинейны.

Так как при этом статистики 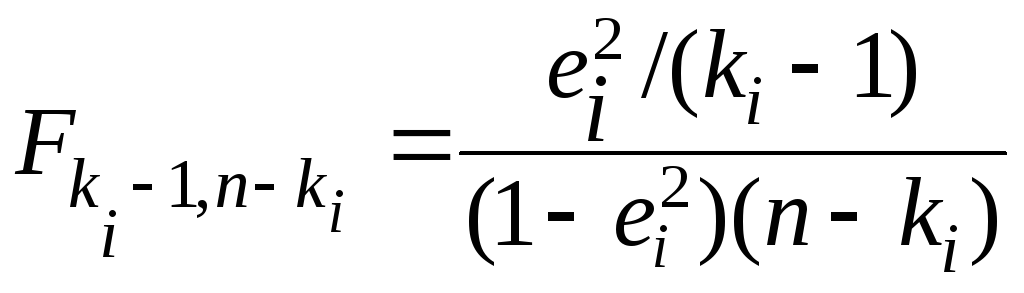принимают значения: F_{4, 95} = (0,3669/4)/[(1– 0,3669)/95] = 13,764; F_{5, 94} = (0,3684/5)/ [(1– 0,3684)/94] = 10,966, а критические значения по таблицам распределения Фишера: при γ = 0,95 F_{4, 95}^(кр.) = 5,66; F_{5, 94} = 4,41; при γ = 0,99 F_{4, 95}^(кр.) = 13,78;

F_{5, 94}^(кр.) = 9,13. Так вычисленные статистики не превосходят табличные критические значения, то при заданном уровне значимости, нелинейную корреляцию следует признать значимой.

Доверительные интервалы для линий регрессии задаются уравнениями вида (6.29).

Для выборочной регрессии = 71,1 + 0,44·(x – 25,8) имеем = 5,69 и уравнения границ доверительного интервала имеют вид: 59,748 + 0,44 x ± 5,69 t_γ {50 + (x – 25,8)/3786}^1/2 ,где t_γ = 1,984 при γ = 0,95 и t_γ = 2,626 при γ = 0,99.

Как функция от x он задаёт две ветви гиперболы, диаметром которой служит выборочная регрессия. Доверительный интервал имеет наименьшую «длину» («ширину»), равную 80,5 t_γ, когда значение независимой переменной x равно её выборочному среднему значению = 25,8 и увеличивается по мере возрастания величины .

Аналогично для выборочной регрессии = 25,8 + 0,19· (y – 71,1):3,725;уравнения границ доверительного интервала: 12,291 + 0,19· y ± 3,725 t_γ {50 + (y – 71,1)/9444,22}^1/2 ; наименьшая «ширина» этого доверительного интервала равна 52,68 t_γ.

Заключительный комментарий: Индивидуальные задания могут выполнятся (и, соответственно, защищаться) отдельными частями в течении семестра (и это довольно удобно!), а могут оформлятся как курсовая работа к концу семестра. Требования к оформлению работ тут довольно различны и, мы считаем, выходят за пределы компетенции нашего Практимума.

.