§3. Вектор скорости.

Для характеристики быстроты движения вводится понятие скорости.

Определение:Средней скоростью движения точки за интервал времени от доназывается векторная величина равная отношению приращения радиус-вектора точки за этот промежуток времени к его продолжительности.

- средняя скорость.

Определение:Скорость (или мгновенная скорость) точки называется векторная величина, равная первой производной по времени от радиус-вектора.

Вектор скорости характеризует движение, как по величине, так и по направлению. Вектор скорости всегда направлен по касательной к траектории в сторону движения.

Определение:Модуль скорости равен первой производной по времени от пройденного пути.

Разложим вектор скорости по базису прямоугольной декартовой системы координат:

, гдеV_x,V_y,V_zпроекции вектора скорости на соответствующую ось, которые соответственно равны:

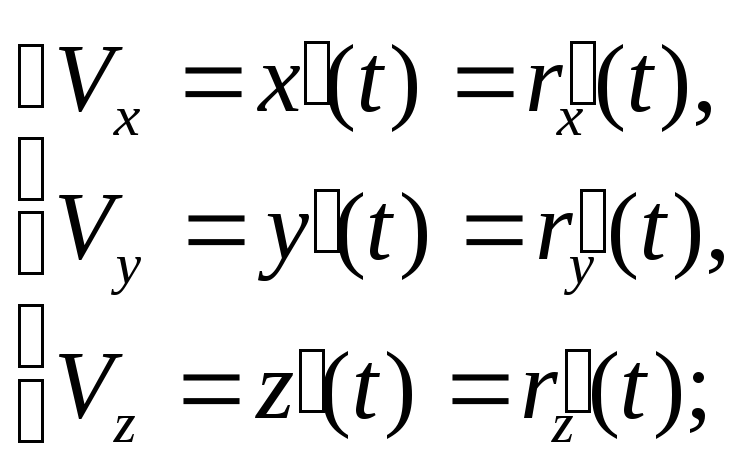
где - это иксовая проекция радиус-вектора материальной точки.

В координатном представлении вектор скорости имеет вид:

Модуль вектора скорости в координатном представлении:

Обратное соотношение.

Представим радиус вектор скорости посредством определенного и неопределенного интеграла:

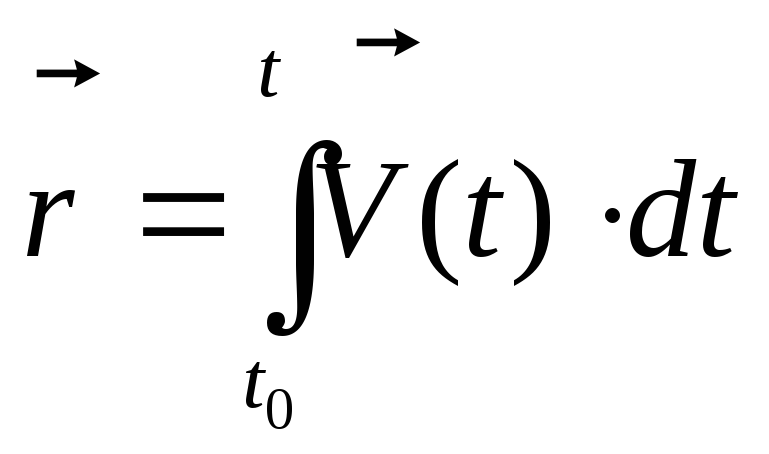
где t,t₀– начальный и конечный момент времени.

Представление пройденного пути через модуль скорости посредством определенного и неопределенного интеграла.

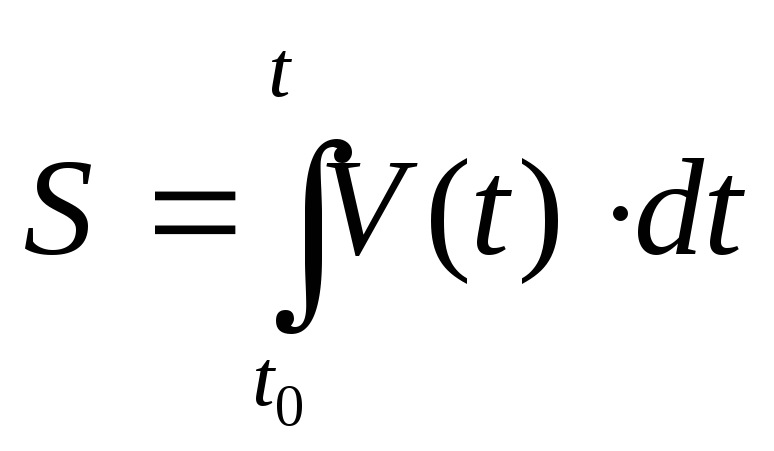
§4. Вектор ускорения.

Для характеристики быстроты изменения вектора скорости точки в механике вводится понятие ускорения.

Определение:Среднее ускорение за интервал времени от доназывается векторная величина равная отношению приращения вектора скорости точки за данный интервал времени к его величине.

Определение:Ускорение (или мгновенное ускорение) точки называется векторная величина, численно равная первой производной по времени от скорости рассматриваемой точки или, что то же самое, вторая производная по времени от радиус-вектора этой точки:

Ускорение можно ввести через предел от среднего ускорения:

Две введенные записи ускорения являются эквивалентными.

Разложим вектор ускорения по базису прямоугольной декартовой системы координат:

где a_x,a_y,a_z– проекции вектора ускорения на ось.

Координатное представление модуля вектора ускорения:

Обратные соотношения:

;

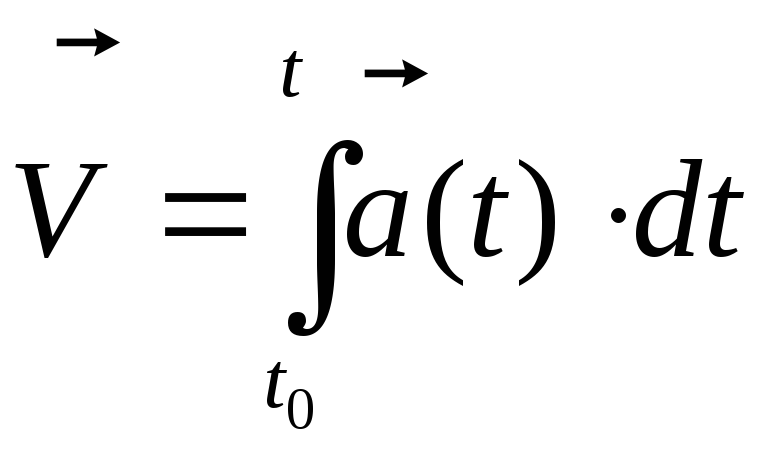
Рассмотрим движение материальной точки вдоль плоской кривой. Ускорение всегда направлено внутрь вогнутости кривой или траектории. Введем два единичных вектора: , который направлен по касательной к траектории и- направлен перпендикулярно траектории в центр кривой.

;

Разложим вектор ускорения по заданным направлениям.

- касательное ускорение.

Определение:Касательное ускорение – векторная величина, характеризующая быстроту изменения вектора скорости по модулю.

- векторное представление.

- скалярное представление.

- нормальное ускорение.

Определение:Нормальное ускорение характеризует быстроту изменения вектора скорости по направлению и вычисляется по формуле:

-где R- радиус кривизны траектории в точке М

Если траектория – окружность, то R– радиус окружности.

В скалярном представлении:

Из свойств составляющих полное ускорение следует, что полное ускорение направленно в сторону вогнутости траектории.

Модуль полного ускорения равен:

Аналогично для вектора полного ускорения: