§ 27. Уравнение состояния идеального газа.

Определение:Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры.

Определение:Уравнением Клайперона называется соотношение, справедливое для постоянной массы идеального газа: .

Определение:Молярной массой любого тела называется физическая величина, равная отношению массы тела к количеству  молей, которое в нём содержится:  = m/,   = m/ ;  = 10 ^–3  m/m_o , где m  масса молекулы данного тела, m_o  масса одной двенадцатой массы атома углерода.

Определение:Молярным объёмом называется физическая величина, равная отношению объёма газа к числу молей, содержащихся в газе: V_ =V/ .

Уравнение состояния идеального газа одного моля p V_ = R T.

Rуниверсальная газовая постояннаяR = 8,31 Дж/(K  моль).

Определение:Уравнением МенделееваКлайперона называется соотношение, справедливое для любого идеального газа: .

Постоянная Больцмана .

Использование постоянной Больцмана, молярного объёма в уравнении МенделееваКлайперона приведёт к следующему результату:эта формула также является уравнением состояния идеального газа, гдеn₀концентрация молекул идеального газа, т.е. их число в единице объёма. Применяя формулу плотности вещества получим ещё один вариант уравнения состояния идеального газа:

.

§ 28. Основное уравнение кинетической энергии газов.

Определение:Основным уравнение кинетической энергии газов есть соотношение: .

Это уравнение выполняется при N = constобщее число молекул в газе, то есть при отсутствии химических реакций; газ может состоять из разнородных молекул.

 суммарная энергия поступательного движения молекул газа, находящихся в сосуде, гдеm_iмасса, аV_i скорость«i  ой» молекулы.

Для однородного газа m_i =m_o , тогда .

Введём средне квадратичную скорость V_квадр. поступательного движения молекул газа:.

Тогда

Подставим данный результат в основное уравнение кинетической теории газов

(*),mмасса всего газа.

Сопоставим полученный результат с уравнением МенделееваКлайперона:

, здесь использовалось полезное соотношение:.

Связь давления, плотности газа и средней квадратичной скорости следует (*):

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа:

.

После подстановки явного выражения для средней квадратичной скорости, получим: .

§ 29. Закон распределения молекул идеального газа по скоростям Максвелла.

Закон распределения молекул идеального газа по скоростям определяет долевое участие молекул однородного газа в тепловом движении при данной температуре со скоростями, заключёнными в интервале от V доV +V. Он выведен теоретически:,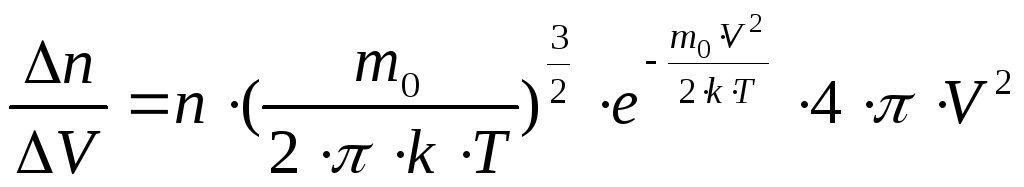

где nчисло молекул в единице объёма (концентрация молекул),

n число молекул из общего их числа, скорости которых лежат в интервале скоростей:,

m₀масса одной молекулы,

kпостоянная Больцмана,

Tтемпература газа.

Чем меньше по величине выбирается интервал скоростей, тем более точный результат даёт данная формула.

Nв единицу объёма, которые[,+]

Графическая иллюстрация данной формулы приведена на графике зависимости относительной концентрации молекул n/Vидеального однородного газа от скорости

Функцией распределения молекул идеального газа по скоростям Максвелла называется выражение:

.

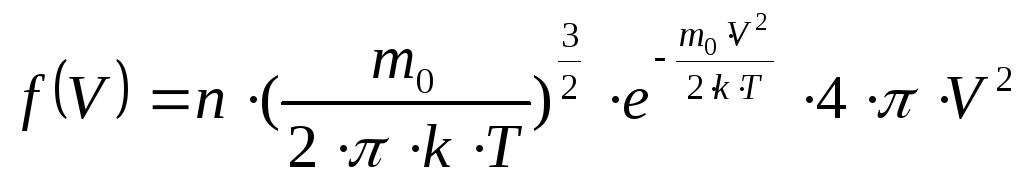С помощью этой функции можно найти все статистически необходимые величины, характеризующие состояние идеального газа.

Вначале найдём наивероятнейшую скорость, т.е. значение скорости, соответствующее максимуму функции Максвелла. С точки зрения физики это такое значение скорости, к которому близки значения скорости большей части молекул. Воспользуемся методом нахождения экстремума функции, т.е. вначале возьмём производную от функции распределения Максвелла по скорости, а затем приравняем полученное выражение к нулю:

.

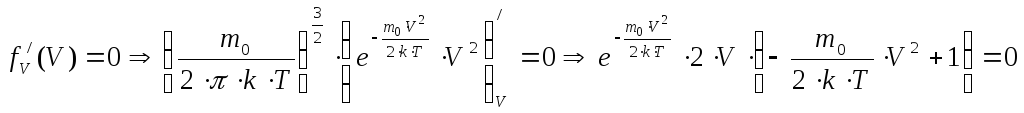Последнее уравнение имеет три решения, т.к. необходимо равенство нулю каждого из множителей:

1. это не физический случай;

2. тривиальный случай;

3.

Средне квадратичную и средне арифметическую скорости находятся интегрированием:

,.