
- •Механика.
- •§1. Механическое движение.
- •§2. Вектор перемещения точки.
- •§3. Вектор скорости.
- •§4. Вектор ускорения.
- •§5. Псевдовекторы.
- •§6. Классификация движения материальной точки.
- •§7. Кинематика твёрдого тела.
- •§8. Первый закон Ньютона. Инерциальная система отсчёта.
- •§9. Сила.
- •§10. Масса. Центр инерции. Импульс.
- •§11.Второй закон Ньютона.
- •§12. Третий закон Ньютона.
- •§13. Закон движения центра инерции.
- •§14. Закон сохранения импульса.
- •§15. Механическая работа.
- •§16.Кинетическая энергия.
- •§17.Потенциальная энергия.
- •§18.Закон сохранения механической энергии.
- •§19. Абсолютно упругий и абсолютно неупругий удары.
- •§20.Момент силы и момент импульса.
- •§21.Момент инерции.
- •Теорема Штейнера.
- •§22.Основной закон динамики вращательного движения.
- •§23.Закон сохранения момента импульса.
- •Термодинамика и молекулярная физика.
- •§24. Предмет молекулярной физики.
- •§25. Статистический, динамический и термодинамический методы исследования.
- •§26. Термодинамические параметры. Термодинамический процесс.
- •§ 27. Уравнение состояния идеального газа.
- •§ 28. Основное уравнение кинетической энергии газов.
- •§ 29. Закон распределения молекул идеального газа по скоростям Максвелла.
- •§ 30. Средняя длина свободного пробега молекул.
- •§ 31. Закон равномерного распределения энергии по степеням свободы молекул.
- •§32. Явления переноса в газах.
- •§33. Явление диффузии.
- •§34. Явление внутреннего трения (вязкости).
- •§35. Явление теплопроводности.
- •§36. Внутренняя энергия термодинамической системы.
- •§37. Количество теплоты и термодинамическая работа.
- •§38. Первое начало термодинамики.
- •§39. Теплоёмкость.
§20.Момент силы и момент импульса.
Для характеристики внешнего механического воздействия на тело, приводящего к изменению его вращательного движения, вводится понятие момента силы. Различают момент силы относительно неподвижной точки (полюса) и относительно неподвижной оси.
Определение: Полюсом называется неподвижная точка, относительно которой происходит сложное трёхмерное движение.
Определение: Моментом силы относительно полюса называется векторная величина, равная векторному произведению радиусвектора, проведённому из полюса в точку приложения силы, на вектор силы,
т.е.
![]() .
В скалярной форме
.
В скалярной форме
![]() ,
где
,
где
![]()
плечо силы относительно рассматриваемого
полюса, т.е. длина перпендикуляра,
проведённого из полюса на линию действия
силы,
угол между вектором силы и радиусвектором.
Момент силы – псевдовекторная величина.
Если линия действия силы проходит через
полюс, то её момент силы равен нулю.
плечо силы относительно рассматриваемого
полюса, т.е. длина перпендикуляра,
проведённого из полюса на линию действия
силы,
угол между вектором силы и радиусвектором.
Момент силы – псевдовекторная величина.
Если линия действия силы проходит через
полюс, то её момент силы равен нулю.

![]()
![]()
![]()
![]()
![]() -
полюс
-
полюс
Момент постоянной силы, при неизменном положении точки её приложения, относительно одного и того же полюса, также постоянен. Момент силы равен нулю, если линия действия силы проходит через полюс.
Определение: Главным моментом (результирующим моментом) системы сил относительно полюса называется векторная величина, равная векторной сумме моментов относительно этого полюса всех сил системы,
т.е.
![]() , где
, где
![]()
радиусвектор,
проведённый из полюса в точку приложения
силы
радиусвектор,
проведённый из полюса в точку приложения
силы
![]() .
.
![]() -
внешняя сила, внутренние силы не создают
моментов, т.к. их моменты
-
внешняя сила, внутренние силы не создают
моментов, т.к. их моменты
взаимно компенсируют друг друга.
Из
третьего закона Ньютона следует, что
![]() , где
, где
![]() внутренние силы, характеризующие
взаимодействие между «i-ой»
и «k-ой»
точками системы, следовательно,
создаваемые внутренними силами моменты
взаимно компенсируют друг друга и при
вычислении главного момента не
учитываются.
внутренние силы, характеризующие
взаимодействие между «i-ой»
и «k-ой»
точками системы, следовательно,
создаваемые внутренними силами моменты
взаимно компенсируют друг друга и при
вычислении главного момента не
учитываются.
Определение: Моментом силы относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента силы относительно произвольной точки данной оси.
В
частном случае вращательного движения
точки по окружности, момент силы, лежащей
в плоскости вращения, равен
![]() ,
где
угол между радиусом окружности и силой
(предполагается, что точка приложения
силы совпадает с местоположением
вращающейся точки). Если же сила находится
под углом к плоскости вращения, то её
момент относительно неподвижной оси
равен
,
где
угол между радиусом окружности и силой
(предполагается, что точка приложения
силы совпадает с местоположением
вращающейся точки). Если же сила находится
под углом к плоскости вращения, то её
момент относительно неподвижной оси
равен
![]() ,
где
,
где![]() - угол наклона силы к плоскости вращения.
Если вращение происходит по окружности
и сила является касательной, то её момент
относительно неподвижной оси равен
- угол наклона силы к плоскости вращения.
Если вращение происходит по окружности
и сила является касательной, то её момент
относительно неподвижной оси равен![]() .
.
Пример: Вычислить момент силы относительно неподвижной оси.

По третьему закону Ньютона:
![]()
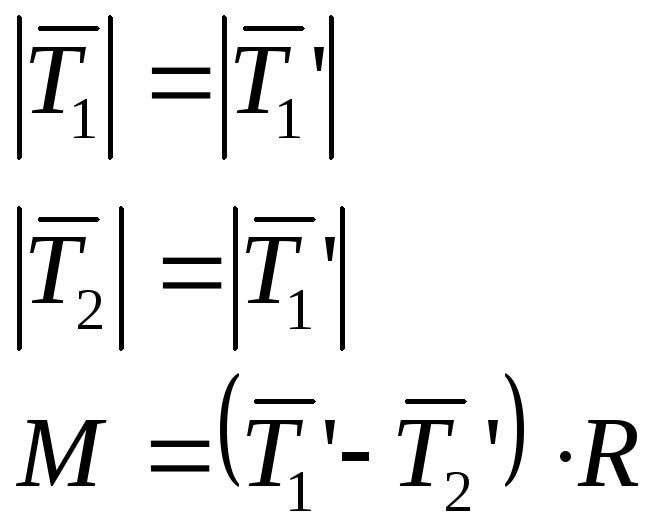
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определение:
Главный
момент (результирующий момент) относительно
неподвижной оси системы сил равен
алгебраической сумме моментов относительно
этой оси всех сил системы, т.е.
![]() .
.
Определение: Моментом импульса (моментом количества движения) материальной точки относительно полюса называется векторная величина, равная векторному произведению радиусвектора, проведённого из полюса в место нахождения материальной точки, на вектор её импульса, т.е.
![]() ,
где
,
где
![]()
масса и скорость материальной точки.
масса и скорость материальной точки.
Момент импульса – псевдовекторная величина. Направление этого вектора находится по тому же правилу, сто и нахождение момента силы (вращение рукоятки буравчика по направлению вектора скорости)
Определение:
Моментом
импульса системы материальных точек
относительно полюса называется векторная
величина, равная векторной сумме моментов
импульсов относительно полюса всех
материальных точек системы,
т.е.
![]() , где
, где![]()
масса, радиусвектор
и скорость «i-ой»
точки системы.
масса, радиусвектор
и скорость «i-ой»
точки системы.
Определение: Моментом импульса материальной точки относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента импульса этой точки относительно произвольной точки данной оси.
Определение: Моментом импульса системы материальных точек относительно неподвижной оси называется скалярная величина, равная проекции на эту ось момента импульса системы относительно произвольной точки данной оси.
В частном случае вращательного движения точки по окружности, момент её импульса равен:
![]() ,
где
угол между радиусом окружности и
скоростью.
,
где
угол между радиусом окружности и
скоростью.
Физический смысл момента импульса: Момент импульса характеризует интенсивность вращательного движения.
