Порядок выполнения работы

1. Установите на объект исследования фотоприемник с исследуемым фотоэлементом и задвиньте бленду осветителя в окно фотоэлемента.

2. Подключите сетевые шнуры измерительного устройства и объекта исследования к сети и включите измерительное устройство тумблером СЕТЬ на его задней панели. При этом должны загореться индикаторы ОБРАТНАЯ, "В" и "мкА" измерительного устройства. На индикаторе "В" должны установиться нули (допускается индикация до значения 2 младшего разряда). После 5 минутного прогрева ручками УСТАНОВКА НОЛЯ на объекте исследования установите нулевое значение на индикаторе "мкА" измерительного устройства.

3. Включите объект исследования выключателем СЕТЬ на его передней панели. При этом должен загореться индикатор СЕТЬ объекта исследования.

4. Дайте лампе осветителя прогреться в течение 15 мин.

5. С помощью кнопки ПРЯМАЯ-ОБРАТНАЯ выберите необходимый режим измерения.

6. Установите необходимый светофильтр.

7. Изменяя значения напряжения с помощью кнопок "+" и "-" и считывая показания фототока с индикатора "мкА", получите данные для построения вольтамперной характеристики.

8. Повторите действия по п. 5...7 настоящего описания для других светофильтров.

9. По окончании работы отключите питание установки выключателями СЕТЬ.

10. Режим работы установки прерывистый – через каждые 45 минут работы делается перерыв на 15 – 20 мин.

Обработка результатов измерений

1. Постройте на миллиметровке ВАХ вакуумного фотоэлемента для различных светофильтров.

2. Постройте зависимость задерживающего потенциала от частоты света:(рис. 1.2), в которойсоответствует максимуму полосы пропускания светофильтра. Значения максимумов полос пропускания светофильтров указаны в справочных материалах. Проведите через полученные точки прямую линию методом наименьших квадратов. Для этого аппроксимируйте зависимость задерживающего потенциала от частоты падающего света уравнением прямой вида:

.

Рассчитайте угловой коэффициент и, а также их погрешности по формулам (П.4)…(П.8) Приложения, где,.

3. Рабочие формулы для определения постоянной Планка h, работы выходаAи красной границы фотоэффекта:

, ,.

4. Погрешности рассчитываются по формулам:

, ,.

Лабораторная работа № 2 изучение спектра атома водорода

Цель работы: наблюдение спектра атомарного водорода; экспериментальное определение постоянной Ридберга и постоянной Планка.

Основные теоретические положения

Спектры атомов подразделяют на спектры испускания и спектры поглощения. Для получения спектра испускания водорода его необходимо разогреть до высокой температуры и излучение пропустить через оптическую систему, состоящую из коллиматора и призмы. При этом на экране, размещенном за призмой, можно наблюдать тонкие цветные линии, образующие спектральную серию, называемую серией Бальмера. Частоты спектральных линий серии Бальмера определяются из формулы:

, , (2.1)

где – постоянная Ридберга.

Кроме одной спектральной серии, расположенной в видимой части спектра, у водорода имеется одна спектральная серия в ультрафиолете, называемая серией Лаймана:

, (2.2)

а также спектральные серии в инфракрасной части спектра:

, (n= 4, 5, 6… – серия Пашена), (2.3)

(n= 5, 6, 7… – серия Брэкета), (2.4)

(n= 6, 7, 8… – серия Пфунда).(2.5)

В низкочастотной области спектр атома водорода простирается вплоть до радиодиапазона. В настоящее время в спектре межзвездного водорода обнаружены спектральные линии, соответствующие длинам волн .

Таким образом, спектр атома водорода разбивается на группы – спектральные серии, каждая из которых представляет собой совокупность спектральных линий с характерной закономерностью в своей последовательности и сходящихся к некоторому пределу – границе серии. Если обратить внимание на структуру соотношений (2.1) – (2.5), то видно, что все они могут быть представлены в общем виде:

, (2.6)

где ицелые числа, причем. Соотношение (2.6) называют обобщенной формулой Бальмера.

Спектр поглощения водорода можно получить при пропускании через него электромагнитного излучения с непрерывным спектром. Тогда после прохождения через коллиматор и призму излучение на экране разворачивается в спектр, представляющий собой радугу, на фоне которой заметны тонкие черные полоски. Черным полоскам соответствуют частоты, определяемые формулой (2.6). Таким образом, спектр излучения и спектр поглощения водорода взаимно дополняют друг друга до радуги.

Атом каждого химического элемента обладает своим уникальным спектром. Поэтому на исследовании спектрального состава излучения основан важнейший метод химического анализа. Наличие в смеси того или иного химического элемента может быть установлено по присутствию в спектре излучения его характерных спектральных линий.

Из анализа спектральных линий может быть получена и другая важная информация, например, о температуре и концентрации вещества в смеси. Данный метод исследования особенно широко применяется в астрофизике, поскольку вещество удаленных космических объектов недоступно для других методов химического анализа. В настоящее время исследование спектров излучения позволило установить химический состав звезд, межзвездной среды и целого ряда других космических объектов.

Изучение атомных спектров послужило ключом к пониманию строения атома. Оказалось, что все попытки объяснения особенностей атомных спектров в рамках классической физики не увенчались успехом. Удовлетворительная теория атома водорода, основанная на положениях, выходящих за рамки классических представлений, была создана в 1913 году датским физиком Нильсом Бором. Данная теория основана на следующих постулатах:

1. Электрон в атоме может находиться лишь на некоторых орбитах, называемых стационарными. Находясь на стационарной орбите, электрон не излучает и не поглощает электромагнитную энергию.

2. При переходе с одной стационарной орбиты на другую электрон излучает или поглощает квант электромагнитной энергии, равный разности энергий соответствующих стационарных состояний:

, (2.7)

–приведенная постоянная Планка.

Из всех орбит электрона в атоме водорода оказываются возможными только те, на которых момент импульса Lэлектрона принимает значения, кратные постоянной Планка. Тогда, считая орбиту круговой, запишем:

, . (2.8)

Равенство (2.8) называется условием квантования орбит.

Определим радиусы стационарных орбит. Для электрона, движущегося по круговой орбите вокруг протона, запишем второй закон Ньютона:

Рис. 2.1. Орбитальный момент импульса электрона.

, (2.9)

где – масса электрона,– заряд электрона,– скорость электрона,– радиус орбиты.

Используя боровское условие квантования (2.8) и исключая из (2.9) , находим:

, . (2.10)

Энергия электрона, находящегося на орбите с номером , определяется соотношением:

, (2.11)

где первое слагаемое в правой части представляет собой кинетическую, а второе – потенциальную энергию взаимодействия электрона с ядром. Из (2.11) с использованием (2.10) и (2.8) находим:

. (2.12)

Используя второй постулат Бора, получаем:

. (2.13)

Сравнивая (2.13) с (2.6), видим, что множитель, стоящий перед скобками в правой части (2.13), представляет собой постоянную Ридберга. Таким образом:

. (2.14)

Теоретическое и экспериментальное значения совпадают с высокой степенью точности, что свидетельствует о справедливости основных положений теории Бора.

Становится очевидной также природа спектральных серий атома водорода. На рис. 2.2 схематически представлены энергетические уровни атома водорода. Серия Лаймана (2.2) образована в результате излучения квантов электромагнитной энергии при переходе электрона с более высоко лежащих энергетических уровней на уровень с, серия Бальмера (2.1) – при переходе на уровень с, серия Пашена (2.3) – при переходе на уровень си т. д.

С

Рис. 2.2. Схема энергетических уровней атома водорода.

пектр поглощения образуется при переходах электронов в атомах водорода снизу вверх. При этом электрон поглощает квант электромагнитной энергии, и атом оказывается в возбужденном состоянии.

Объединенная формула Бальмера (2.6) позволяет по известной частоте (длине волны) спектральной линии определить постоянную Ридберга:

. (2.15)

Соотношение (2.14) позволяет определить по известному значению постоянной Ридберга постоянную Планка:

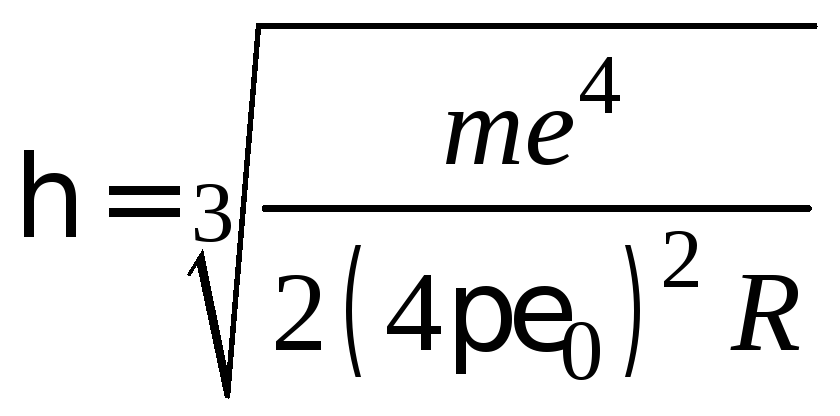. (2.16)