Обработка результатов эксперимента

1. Определите угол дифракции для зелёной линии спектра, первого порядка по формуле φ=(N - N')/2. Найдите среднее значение и, зная длину волны для зеленой линии, рассчитайте период решетки по формуле (2.4).

2 По результатам расчёта пункта 1 рассчитайте число штрихов на 1 мм ширины решетки по формуле n=1/d.

3. Определите угол дифракции для красной линии спектра первого порядка аналогично пункту 1.

4. Зная углы дифракции на красной и зеленой линиях и период решётки, рассчитайте угловую дисперсию решётки по формуле (2.7) и для двух спектральных линий по формуле (2.8). Сравните результаты двух способов вычисления и сделайте выводы.

5. Вычислите разрешающую способность но формуле (2.10). Для этого найдите полное число штрихов решетки N=nl, где l - ширина освещенной светом части решётки, l=0,05 мм.

Расчет погрешностей

1. Вычислите погрешности определения периода решетки d. Из рабочей формулы d = тλ/sinφ следует, что погрешность величины d определяется погрешностью величины φ. Согласно методу определения погрешности косвенных измерений погрешность величины d рассчитайте по формуле:

,

где Δφ=Δ(N-N')/2=Δ(ΔN)/2 - погрешность измерения угла φ для зеленой линии. Величину Δ(ΔN) рассчитайте по методу прямых многократных измерений с учётом систематической ошибки измерений Δ(ΔN)_пр= 0.2°:

,

где Δ(ΔN)_сл рассчитайте по формуле (П. 3) (см. приложение).

2.Вычислите погрешности определения числа штрихов на единицу длины п. Согласно рабочей формуле n=1/d погрешность определите по методу косвенных измерений:

.

3.Вычислите погрешности величины дисперсии D. Для формулы D=(φ_кр - φ_зел)/(λ_кр - λ_зел) погрешность величины D рассчитайте через погрешность величины (φ_зел – φ_син):

.

Для формулы погрешность величины D рассчитайте через погрешность величин d и φ:

.

4. Вычислите погрешности определения разрешающей способности R, Из рабочей формулы R=m N=m n l следует, что погрешность величины R определяется погрешностью величины п:

Лабораторная работа № 3

ИССЛЕДОВАНИЕ ЗАКОНА МАЛЮСА И ПРОХОЖДЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА ЧЕРЕЗ ФАЗОВУЮ ПЛАСТИНКУ

Цель работы: Изучение поляризации света при прохождении света через поляризатор: проверка выполнения закона Малюса; определение коэффициентов пропускания поляроид. Определение эллиптичности света и разности показателей преломления обыкновенного и необыкновенного лучей при прохождении света через кристаллическую пластинку.

Основные теоретические положения

Виды поляризации света

Волна, в которой направление колебаний светового вектора упорядочено каким-либо образом, называется поляризованной. Если колебания вектора происходят только в одной плоскости, проходящей через луч, то такая поляризация называется линейной. Плоскость, в которой колеблется вектор , называется плоскостью поляризации.

Рис.3.1. Схема сложения двух колебаний, плоскости поляризации которых взаимно перпендикулярны	Рис.3.2. Схема разложения вектора E0 на две составляющие

Другой вид поляризации состоит в том, что вектор вращается вокруг направления распространения волны, одновременно изменяясь периодически по модулю. При этом конец вектора описывает эллипс (в каждой точке среды). Такая волна называется эллиптически-поляризованной. или поляризованной по кругу, если конец вектора описывает окружность. В зависимости от направления вращения вектора различают правую и левую эллиптические (или круговые) поляризации. Эллиптическая поляризация – это наиболее общий вид поляризации волны, переходящий при определенных условиях в линейную и круговую поляризации.

Эллиптически поляризованный свет можно представить как наложение двух когерентных линейно поляризованных световых волн, плоскости колебаний которых взаимно перпендикулярны (рис. 3.1). Проекции результирующего вектора определяются выражениями

, (3.1)

где δ - разность фаз между компонентами вектора. При δ=0,π эллипс вырождается в прямую и результатом сложения является: линейно поляризованный свет. При δ= π/2 и равенстве амплитуд складываемых волн А₁=А₂ эллипс превращается в окружность, результатом сложения является свет, поляризованный по кругу.

Естественный свет - это совокупность конечных электромагнитных волн оптического диапазона, испускаемых обычными (не лазерными) источниками, например, раскаленными твердыми телами или возбужденными атомами газа. Направления колебаний векторов таких волн лежат в плоскости, перпендикулярной направлению распространения волн, и могут быть любыми. Поэтому, при сложении таких волн результирующий вектор в любой фиксированной точке среды быстро (с частотой ν=1/τ = 10⁸с^-1) и беспорядочно меняется по величине и направлению.

Поляризаторы

Свет поляризуется при отражении и преломлении на границе раздела двух диэлектриков и благодаря явлениям двойного лучепреломления и дихроизма, возникающим при прохождении через анизотропные диэлектрики. Из естественного света можно получить свет с любым видом поляризации с помощью приборов, называемых поляризаторами.

Принцип действия этих приборов может быть основан на любом из физических явлений, перечисленных выше. Визуально поляризованный свет нельзя отличить от неполяризованного, поэтому поляризаторы можно использовать в качестве анализаторов - для определения характера и степени поляризации интересующего нас света.

Закон Малюса

Рассмотрим идеальный поляризатор, преобразующий свет в линейно поляризованный. Этот поляризатор свободно пропускает колебания светового вектора, параллельные плоскости, называемой плоскостью пропускания поляризатора. Колебания же, перпендикулярные к этой плоскости, задерживаются им полностью.

Пусть на анализатор падает линейно поляризованный свет, вектор которого составляет угол α с плоскостью пропускания РР (рис. 3.2). Анализатор пропускает только ту составляющую вектора , которая параллельна плоскости пропускания РР, т. е.. Так как интенсивность пропорциональна квадрату модуля светового вектора (I~E²), то интенсивность прошедшего света

I=I₀ cos²α, (3.2)

где I, I₀ - интенсивности прошедшего и падающего линейно поляризованного света. Это соотношение называется законом Малюса.

Реальный поляризатор является несовершенным. Такой поляризатор частично пропускает как параллельную составляющую колебания, так и перпендикулярную составляющую Введя коэффициенты пропускания соответствующих составляющих колебанийдля интенсивности света, проходящего через поляризатор, можно записать следующее выражение:

, (3.3)

где I₀ cos²α и I₀ sin²α - интенсивности составляющих колебаний.

Для реального поляризатора <1.

Двойное лучепреломление

Почти все прозрачные кристаллические диэлектрики оптически анизотропны. Вследствие этого возникают явления, называемые двойным лучепреломлением. Оно заключается в том, что падающий на кристалл луч света разделяется внутри кристалла на два луча, распространяющихся, как правило, в различных направлениях и с разными скоростями.

Различают кристаллы одноосные и двуосные. У одноосных кристаллов один из преломленных лучей подчиняется обычному закону преломления. Его называют обыкновенным и обозначают буквой или индексом о. Другой луч называют необыкновенным с индексом е, он не подчиняется обычному закону преломления. Даже при нормальном падении светового луча на поверхность кристалла необыкновенный луч может отклоняться от нормали и может не лежать в плоскости падения.

У одноосных кристаллов имеется выделенное направление, называемое оптической осью OO, вдоль которого обыкновенная и необыкновенная волны распространяются, не разделяясь пространственно и с одинаковой скоростью. У двуосных таких направлений два.

Любую плоскость, проходящую через оптическую ось, называют главным сечением или главной плоскостью кристалла, но обычно под этим названием имеют в виду плоскость, проходящую через световой луч и оптическую ось.

Лучи о и е линейно поляризованы. Колебания вектора луча о совершаются в направлении, перпендикулярном главному сечению кристалла для обыкновенного луча. Колебания же вектора луча е совершаются в главном сечении кристалла для необыкновенного луча. Заметим, что практически при любой ориентации оптической оси и падающего на кристалл луча, можно считать, что поляризации лучей о и е взаимно ортогональны. Это возможно, поскольку угол между лучами о и е достаточно мал.

Существуют кристаллы, в которых один из лучей (о или е) поглощается сильнее другого. Это явление называют дихроизмом. Явление дихроизма используют для изготовления поляризаторов, линейно поляризующих проходящий через них свет за счёт почти полного поглощения одного из лучей. Их называют поляроидами. Поляроид - это стеклянная подложка, на поверхность которой тонкой плёнкой нанесены ориентированные одинаковым образом прозрачные кристаллы. Толщина плёнки поляроида составляет порядка ~ 0.1 мм. Такой толщины достаточно, чтобы один из лучей почти полностью поглотился.

Анизотропия кристалла приводит к неравенству скорости распространения о- и е- волн. Скорость v_o не зависит от направления в кристалле, скорость v_e по мере отклонения луча е от направления оптической оси (вдоль которой скорости обоих лучей одинаковы) будет все больше отличаться, достигая максимального различия в направлении, перпендикулярном оптической оси.

Рис. 3.3. Волновые поверхности Рис. 3.4. Поляризатор - фазовая пластинка вторичных волн о и е в положительном и отрицательном кристалле

Одноосные кристаллы, характеризуются показателем преломления
обыкновенноголуча n_o =c/v_o и показателем преломления необыкновенного
луча, перпендикулярного оптической оси,п_е = c/ν_e. Если ν_o>v_e (n_o<n_e), кристаллы называют положительными, если v₀<v_e (n_o>n_e), - кристаллы называют отрицательными.

Кристаллические пластинки в четверть волны и в полволны

Рассмотрим кристаллическую пластинку, вырезанную вдоль оптичес- кой оси OO. При нормальном падении света на такую поверхность лучи о и е распространяются вдоль нормали, пространственно не разделяясь, но приобретают разность фаз, обусловленную неравенством показателей прелом

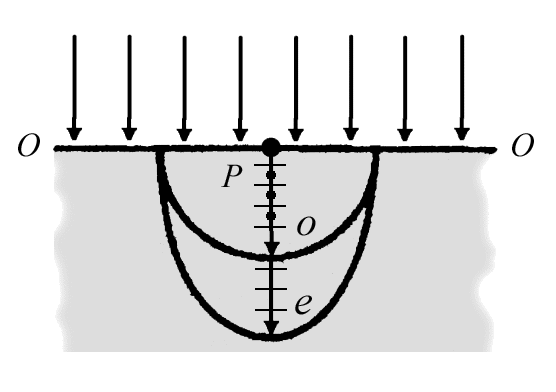
ления. На рис. 3.3 показала волновая поверхность Вторичных волн о и е, испускаемых точкой Р на поверхности кристаллической пластинки (для положительного кристалла (а) и для отрицательного кристалла (б)). Волновая поверхность волны о - сферическая, так как скорость волны в любом направлении одинакова Волновая поверхность волны е - эллипсоид. Стрелками указаны направления распространения лучей в кристалле.

Пусть толщина пластинки d удовлетворяет соотношению

(3.4)

где d(n_o—n_e) оптическая разность хода лучей о и е, знак плюс соответствует отрица­тельному кристаллу, знак минус - положи­тельному. Тогда разность фаз волн o и e составит, и пластинка называется пластинкой в четверть волны. Если угол между плоскостью поляризации падающего света и главной плоскостью пластинки α=0,π/2 (рис. 3.4), то плоскость поляризации падающего света не изменится, так как в первом случае в кристалле будет распространяться только е-волна, во втором случае - только o-волна.

Если α=0,π/2, то волна разделится на равные по интенсивности о и е- волны, которые при прохождении через кристалл приобретут разность фаз δ, указанную выше. При этом вышедший из пластинки свет, образованный сложением двух волн, будет иметь круговую поляризацию (дихроизмом пренебрегаем). Если α будет иметь любое другое значение, то свет будет иметь эллиптическую поляризацию.

У пластинки в полволны толщина d удовлетворяет соотношению

(3.5)

и разность фаз составит δ= 2 πm+π. Если угол между плоскостью поляризации падающего света и главной плоскость кристалла α= 0, π/2, то плоскость поляризации падающего света не изменится, если α будет иметь любое другое значение, то пластинка поворачивает плоскость колебаний на угол 2α симметрично главному сечению пластинки.

Экспериментальная установка и методика эксперимента

Поляризация света изучается при помощи оптической скамьи (рис. 3.5). В качестве источника света на оптическую скамью устанавливается лазер (1), линейно поляризованное излучение которого обладает высокой степенью поляризации. Ориентация плоскости поляризации излучения зависит от положения лазера в юстировочном узле.

Рис.3.5 Вид установки.

Для изучения закона Малюса на пути пучка лазерного света устанавливается поляроид (3) - анализатор лазерного излучения, который может вращаться вокруг оптического канала. Вышедший после анализатора свет попадает на светочувствительный элемент (4), подключенный к мультиметру. Показания с мультиметра снимаются в наиболее чувствительном режиме микроамперметра. Измеряемая амперметром сила тока пропорциональна световому потоку, падающему на фотоэлемент.

Так как лазерное излучение обладает высокой степенью поляризации, его можно использовать для определения коэффициентов пропускания τ^║ и τ^┴ поляроида. Если плоскость пропускания поляроида сориентирована параллельно плоскости поляризации лазерного излучения, то интенсивность света, выходящего из поляроида, максимальна, и из формулы (3.3) следует:

I_max = τ^║I₀ , отсюда

τ^║= I_max/ I₀ = i_max / i₀ , (3.6)

где i_max , i₀ - соответствующие значения силы тока.

Если плоскость пропускания поляроида сориентирована перпенди­кулярно плоскости поляризации лазерного излучения, то интенсивность света, выходящего из поляроида, минимальна: I_min =τ^┴I₀, отсюда

τ^┴ = I_min / I₀ = i_min / i₀ . (3.7)

Во второй части работы между лазером и анализатором помещается кристаллическая пластинка (2) из слюды известной толщины d. Перед установкой пластинки анализатор устанавливается в такое положение, при котором наблюдается минимальная интенсивность света. Вращая пластинку вокруг своей оси, можно убедиться в наличии таких четырех ее положений, при которых опять будет наблюдаться минимум интенсивности. Эти положения соответствуют перпендикулярной или параллельной ориентации оптической оси ОО пластинки относительно плоскости главного пропускания анализатора. В первом случае внутри кристалла распространяется только обыкновенная волна, во втором случае - необыкновенная.

При этом поляризация проходящего через пластинку света не меняется. Если сориентировать пластинку под углом 45° относительно любого из таких положений, то в пластинке распространяются равные по интенсивности о- и е-волны. При этом из пластинки произвольной толщины выходит эллиптически поляризованный свет.

Эллиптичность света определяется с помощью анализатора. Если большая ось эллипса поляризации сориентирована параллельно плоскости пропускания анализатора, то наблюдается максимум интенсивности света I_max. Если малая ось эллипса параллельна плоскости пропускания, то наблюдается I_min. Эллиптичность вышедшего света, которая определяется как отношение малой и большой полуосей эллипса alb, рассчитывается по формуле:

tg ε= a/b = , (3.8)

где i_max , i_min - соответствующие максимальной и минимальной интенсивно­сти показания микроамперметра.

При выполнении условия ориентации оптической оси OO фазовой пластинки под углом 45° к плоскости поляризации падающего света разность фаз δ и эллиптичность ε связаны между собой простым соотношением:

δ = 2 ε . (3.9)

Эта формула легко иллюстрируется следующими примерами: при разности фаз между волнами о и е δ=0 выходящий свет линейно поляризован ε=0 и

tg ε=0; при δ=π свет также линейно поляризован ε = π /2 и tg ε =∞; при δ=π/2,3π/2 свет имеет круговую поляризацию и tg ε=1.