Вариант 26

Даны вершины треугольника A(-12; -2); B(4; 10); C(-6; -10). Показать, что этот треугольник прямоугольный и составить уравнение высоты, проведенной из вершины прямого угла.
Написать уравнение прямой, параллельной прямой и отсекающей от первого координатного угла площадь, равную 5.
Основание равнобедренного треугольника имеет уравнение. Одна из боковых сторон имеет уравнение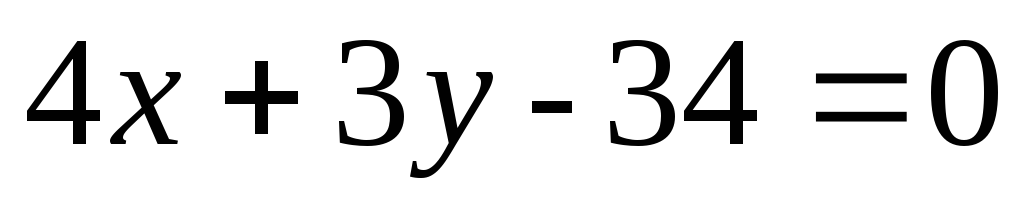. Найти уравнение другой боковой стороны, если известно, что она проходит через точкуM(8; 9).
Сторона AB и DC параллелограмма заданы уравнениями и, диагонали его пересекаются в точкеM(1; 4). Найти длину высоты параллелограмма из вершины B.
Найти расстояние от точки пересечения плоскостей,,до плоскости, проходящей через точкиM₁(1; 4; 2), M₂(2; 3; 1), M₃(1; 1; 2).
Плоскость α проходит через точку M₁(1; 3; 1) параллельно плоскости 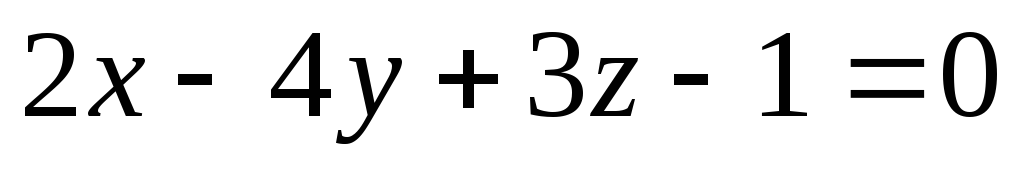. Плоскость β проходит через точкуM₂(5; -1; 2) и содержит ось . Найти угол между плоскостями α и β.
Плоскость α проходит через точку P(3; -1; 2) и отсекает на оси отрезок вдвое больше, чем на осии втрое больше, чем на оси. Плоскость β задана уравнением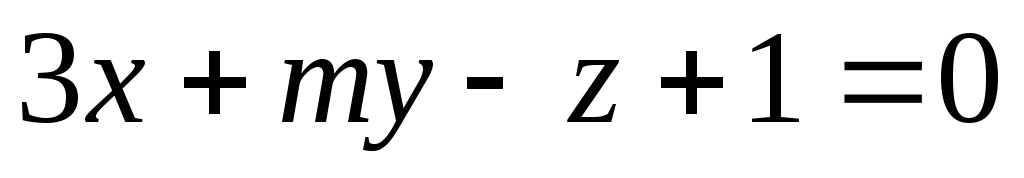. При какомm плоскости будут перпендикулярны?
Написать каноническое уравнения прямой .
Найти расстояние от точки P(1; 3; 5) до прямой .
Найти периметр треугольника с вершинами M₁(2; 4; 5), M₂(3; 8; 13), M₃(-1; 0; 5). Найти уравнение треугольника и угол между сторонами M₁M₂ и M₁M₃.
Через точку M₁(2; 3; 6) провести плоскость перпендикулярную прямой .

Вариант 27

Вычислить координаты точки пересечения перпендикуляров, восстановленных из середин сторон треугольника, вершинами которого являются точки A(2; 3), B(0; -3), C(5; -2).
Написать уравнение прямой, отсекающей на оси отрезок, величина которого равна 3, и наклоненной к осипод углом 135º.
Вычислить тангенс острого угла между прямыми ,.
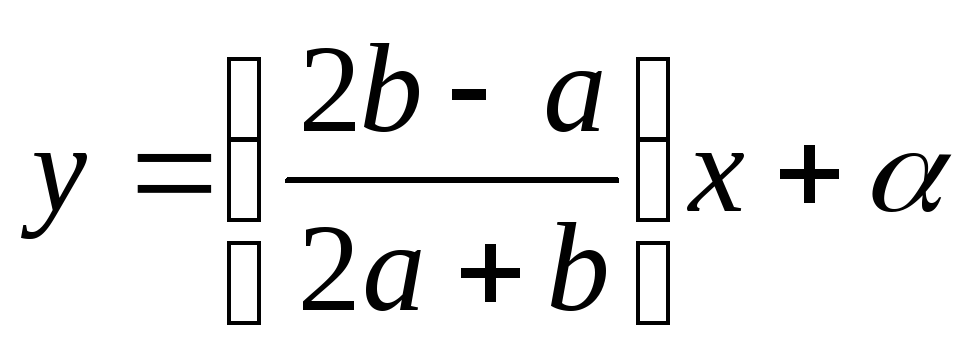На прямо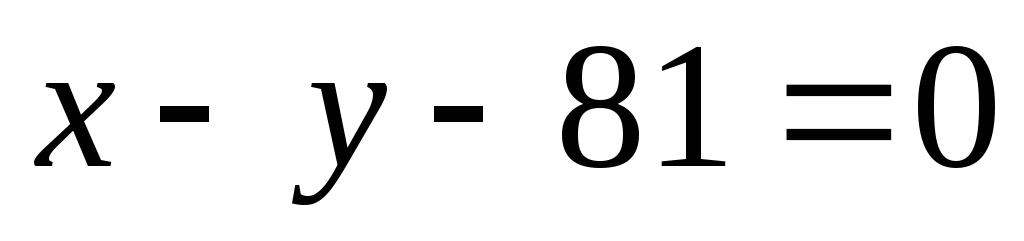й найти такую точку, у которой абсцисса в десять раз больше ординаты. Найти расстояние от найденной точки до прямой.
Дан тетраэдр с вершинами A(2; 0; 1), B(0; 0; 3), C(1; 2; 1), D(4; 3; 2). Найти угол между гранями ABC и ACD. Составить уравнение плоскости, проходящей через вершину D параллельно грани ABC.
Составить уравнение плоскости, проходящей через точку M₁(3; 5; 1) и M₂(4; 2; 3) и параллельной вектору . Найти расстояние от точкиP(5; -2; 4) до построенной плоскости.
Составить уравнение плоскости, проходящей через точки M₁(1; 1; 1), M₂(2; 3; 4) и перпендикулярной плоскости . Полученное уравнение привести к уравнению в отрезках и построить.
Написать каноническое уравнения прямой .
Составить уравнение прямой, проходящей через точку B(3; 4; -4) параллельно прямой . При какомm построенная прямая будет перпендикулярна прямой .
Найти проекцию точки M(-1; -1; 0) на плоскость .
При каких значениях A и B прямая лежит на плоскости. При А=1, В=-2. Найти угол между прямой и плоскостью.

Вариант 28

Даны вершины треугольника A(2; 1), В(0; 7), С(-4; -1). Найти уравнение его медиан и точку их пересечения.
Составить уравнение прямой, которая проходит через точку M₁(2; -5) и отсекает отрезок втрое больше, чем на оси ординат (считая каждый отрезок, направленным от начала координат).
Даны уравнения сторон треугольника (АВ),(ВС),(АС). Найти угол между высотой, проведенной из вершины В и прямой, проведенной через точку С параллельно АВ.
Дана прямая . Найти уравнение прямой, параллельной данной и отстоящей от нее на расстоянии четырех единиц.
Плоскость α проходит через точку Р(2; 1; 1) и отсекает на осях ох и oy отрезки, соответственно равные 4 и -6. Плоскость β задана уравнением . При какихm и n плоскости будут параллельны?
Плоскость α проходит через точку M₁(5; 3; 2) и параллельна двум векторам и. Плоскость β проходит через точку Р₁(1; 1; 1), Р₂(2; 3; 2) и Р₃(3; 4; 2). Найти угол между плоскостями α и β.
Вычислить расстояние между плоскостям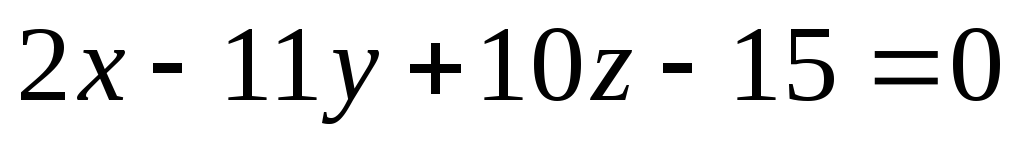и и.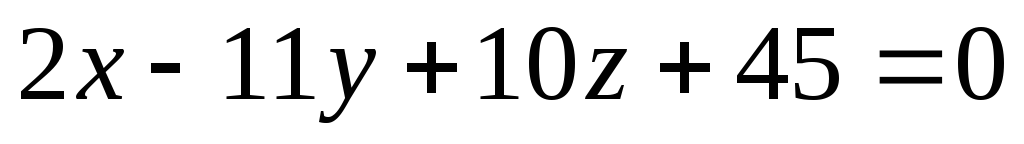
Написать каноническое уравнения прямой .
Найти точку симметричную точке С(-1; 2; 0) относительно прямой ,,.
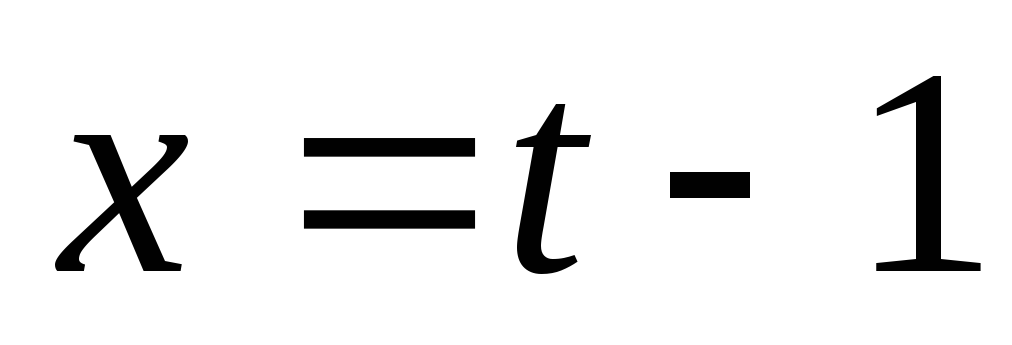При каком n плоскость будет параллельна прямой? При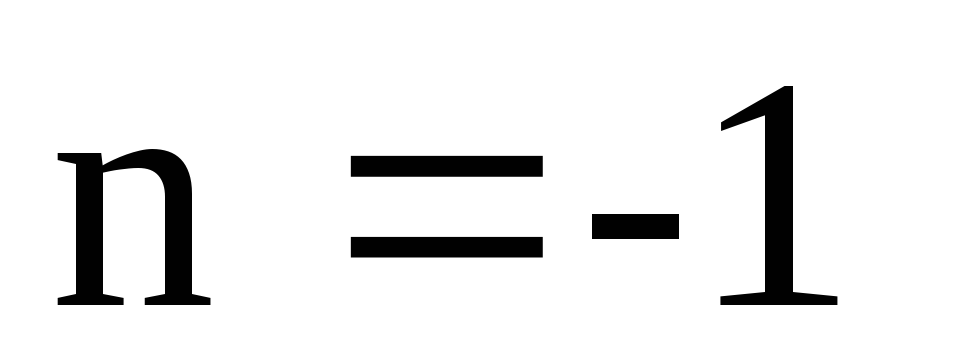найти точку пересечения и угол между прямой и плоскостью.
Прямая α проходит через точку M₁(3; 4; 7) и M₂(-1; 3; 3). Прямая β проходит через точку Р(3; 2; -1) параллельно прямой . Найти угол между прямыми α и β.