
- •Пермь 2007 Вариант решения заданий
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), Найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
- •Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции .
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Дифференциальное и интегральное исчисление функции одной переменной
Индивидуальные задания
-
Пособие разработано ст. преп. Смышляевой Т. В.
Одобрено методической комиссией кафедры «Высшая математика»
© 2007, каф. «Высшая математика» ПГТУ
Пермь 2007 Вариант решения заданий
-
Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции

Решение:
-
Придаем аргументу
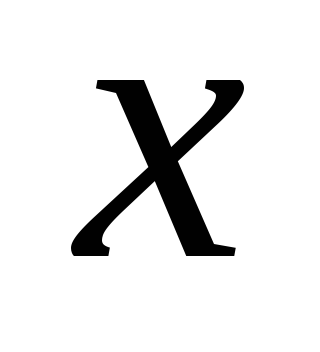 произвольное приращение
произвольное приращение
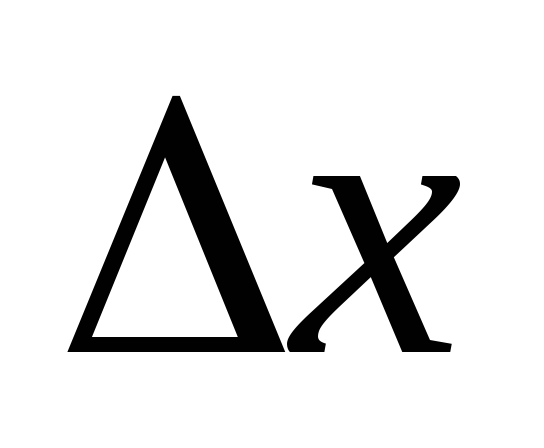 и,
подставляя в данное выражение функции
вместо
и,
подставляя в данное выражение функции
вместо
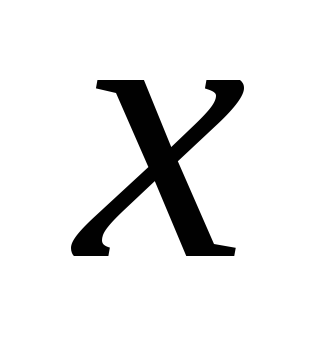 наращенное значение
наращенное значение
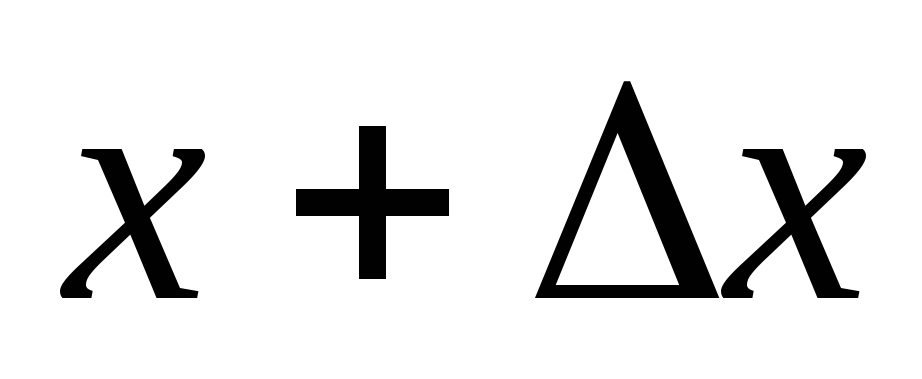 ,
находим наращенное значение функции
,
находим наращенное значение функции
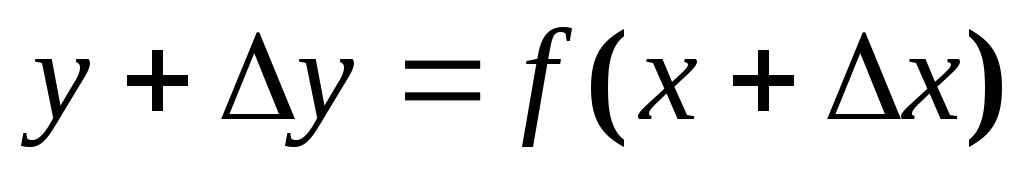
В данном случае
![]()
-
Находим приращение функции
![]()
-
Делим приращение функции на приращение аргумента, т. е. составим отношение
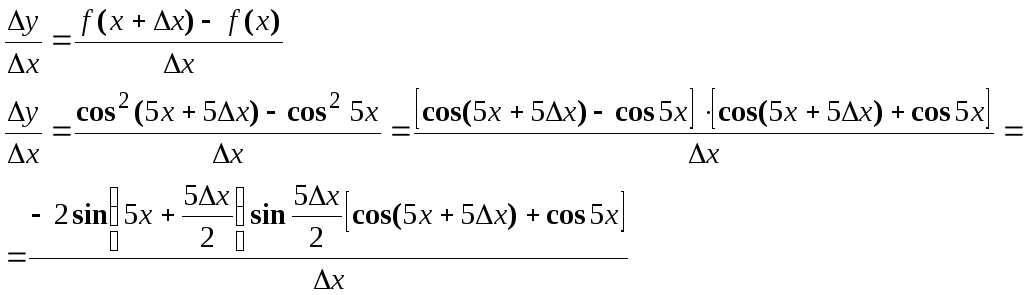
-
Ищем предел этого отношения при
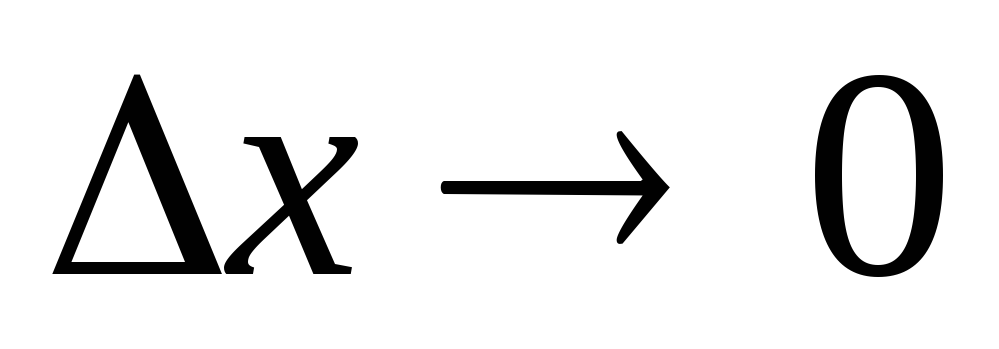 .
Этот предел и даст искомую производную
.
Этот предел и даст искомую производную
 от функции
от функции
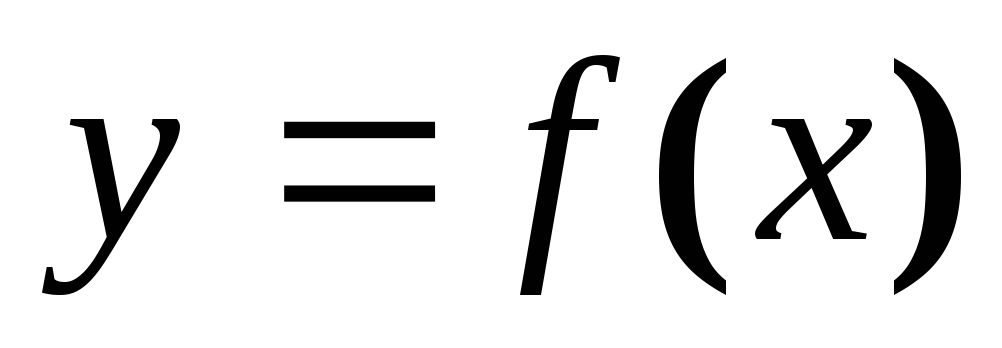 ;
;
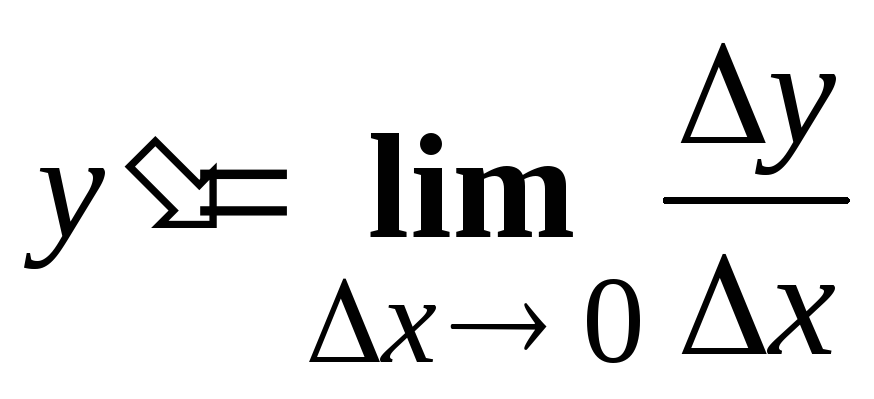
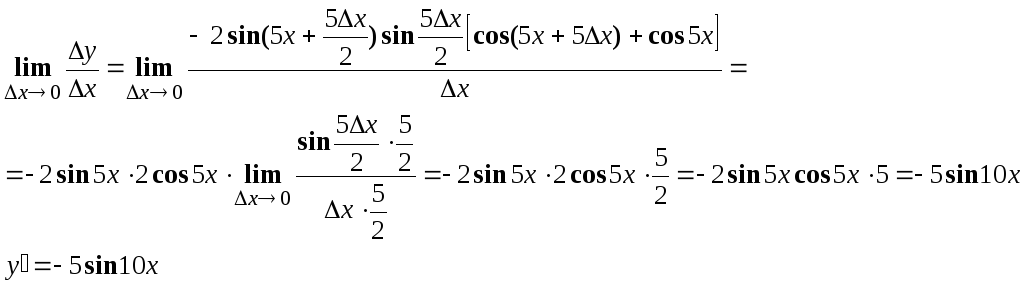
-
Производная сложной функции
Производная сложной функции равна произведению её производной по промежуточному аргументу на производную этого аргумента по независимой переменной.
![]()
Найти производные следующих функций:
![]()
![]()
![]()
![]()
![]()
![]()
Решение:
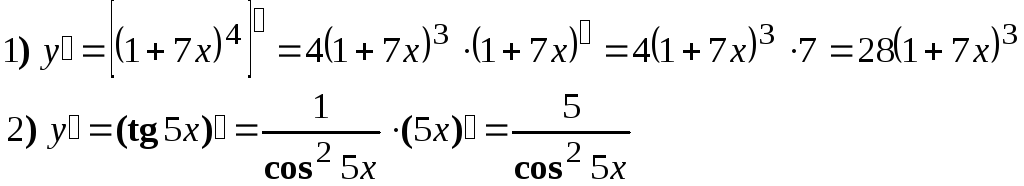

-
а) Производная неявной функции
Найти
![]() для данной неявной функции
для данной неявной функции
![]()
Решение:
Дифференцируем по
![]() обе части равенства, где
обе части равенства, где
![]() есть функция от
есть функция от
![]() ,
получим
,
получим
![]() .
.
Учитывая, что
![]() ,
получаем
,
получаем

б) Логарифмическое дифференцирование
Логарифмическое дифференцирование
полезно применять для нахождения
производной от показательно - степенной
функции
![]() ,
где
,
где
![]() - функции от
- функции от
![]() и когда заданная функция содержит
логарифмирующиеся операции (умножения,
деления, возведения в степень, извлечение
корня).
и когда заданная функция содержит
логарифмирующиеся операции (умножения,
деления, возведения в степень, извлечение
корня).
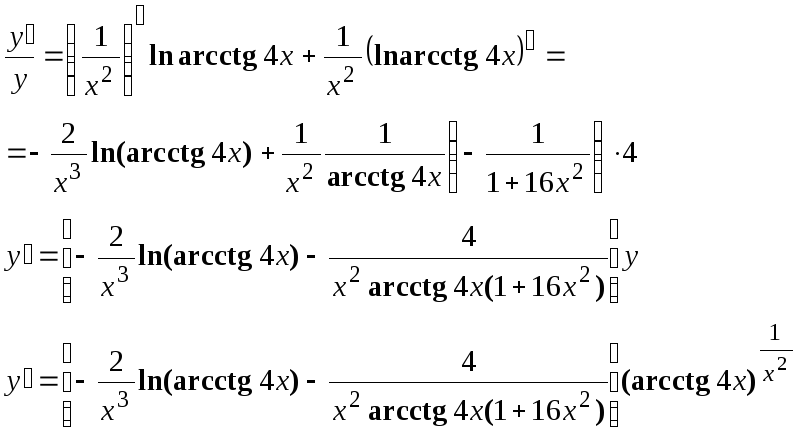
Найти производные следующих функций:
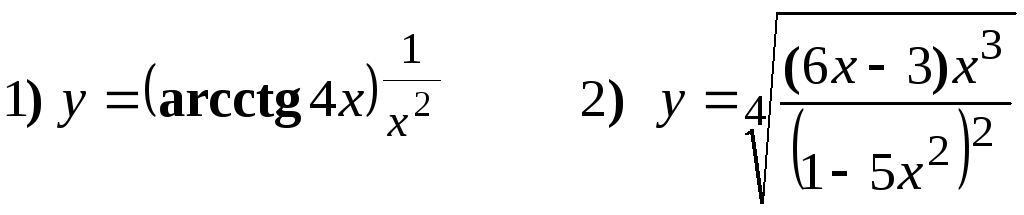
Решение:
Применяется логарифмическое дифференцирование, последовательно находим:
![]()
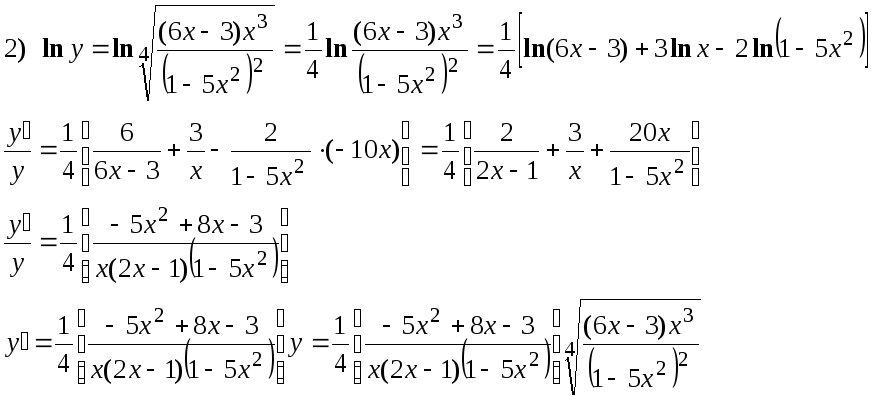
в) Производная от функции, заданной параметрически

Производная
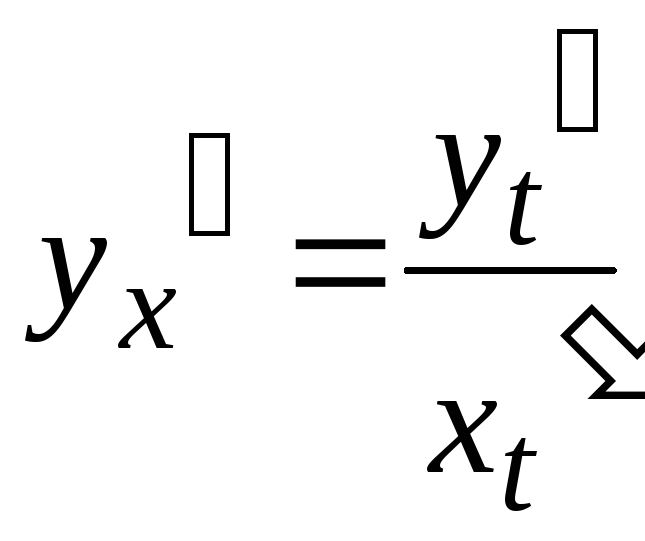
Найти производную
![]() для функции, заданной параметрически
для функции, заданной параметрически
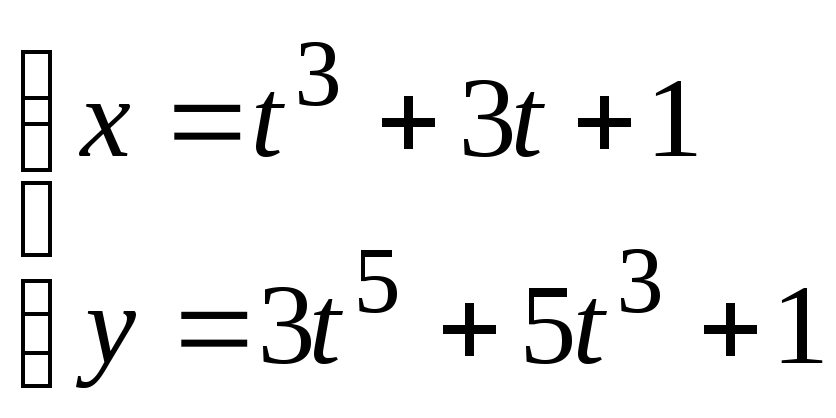
Решение:
Найдем
![]() .
Следовательно,
.
Следовательно,
![]()
-
Показать, что функция
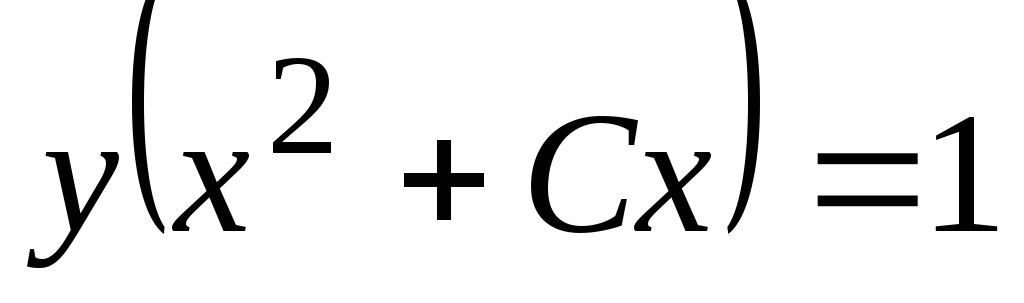 обращает уравнение
обращает уравнение
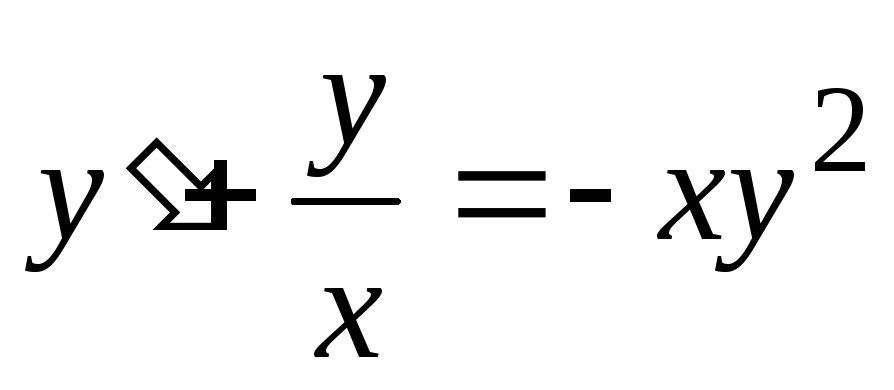 в тождество.
в тождество.
Решение:
Выразим
![]() в
явном виде
в
явном виде
![]() .
Найдем
.
Найдем
![]()
Подставляем
![]() и
и
![]() в левую часть уравнения, получаем
в левую часть уравнения, получаем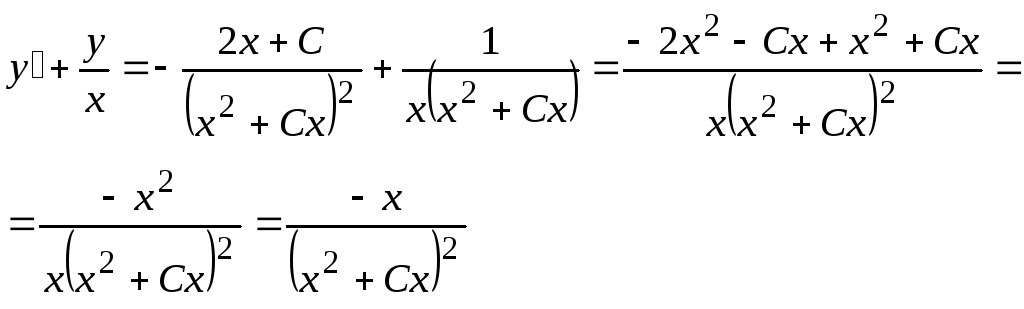
Подставляем
![]() в
правую часть равенства, получаем
в
правую часть равенства, получаем
![]()
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
-
Производные высших порядков
а) Производная явной функции
![]()
Решение:
Дифференцируя функцию
![]() ,
получим
,
получим
![]() .
.
Дифференцируя производную
![]() ,
получим
,
получим
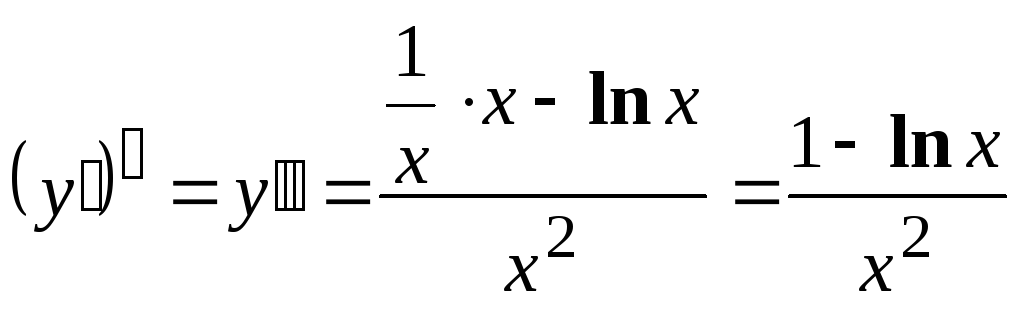
б) Производная неявной функции
Для данной неявной функции найти
![]() .
.
![]()
Решение:
Дифференцируем по
![]() обе части равенства, где
обе части равенства, где
![]() есть
функция от
есть
функция от
![]() ,
получаем
,
получаем![]()
Отсюда найдем
![]() .
.
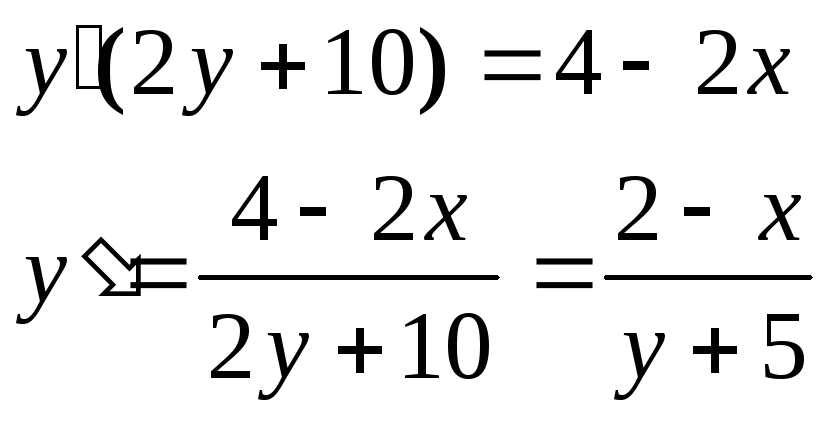
Найдем
![]() :
:
![]()
Подставляем в левую часть найденную
производную
![]() ,
получаем:
,
получаем:
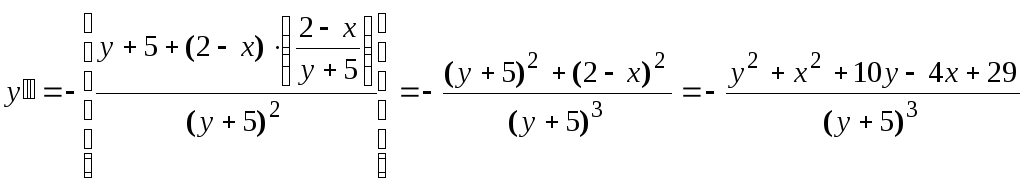 .
.
Учитывая, что
![]() ,
получим
,
получим
![]() или
или
![]()
-
Производная от функции, заданной параметрически
Для функции, заданной параметрически,
найти
![]() .
.

Решение:
Находим производные
![]() по параметру
по параметру
![]() .
.
![]()
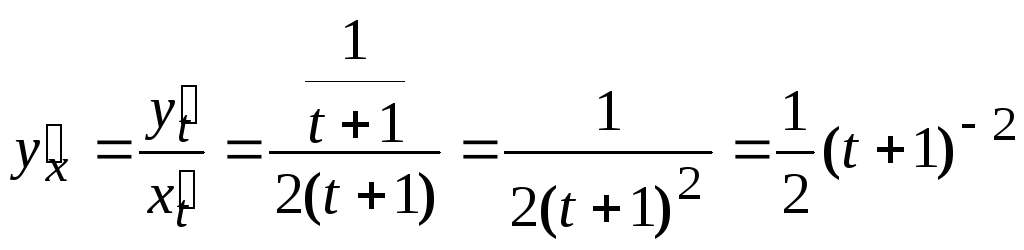
Далее находим производную от
![]() ,
а затем искомую вторую производную от
,
а затем искомую вторую производную от
![]() как отношение производных от
как отношение производных от
![]() и
от
и
от
![]() .
.
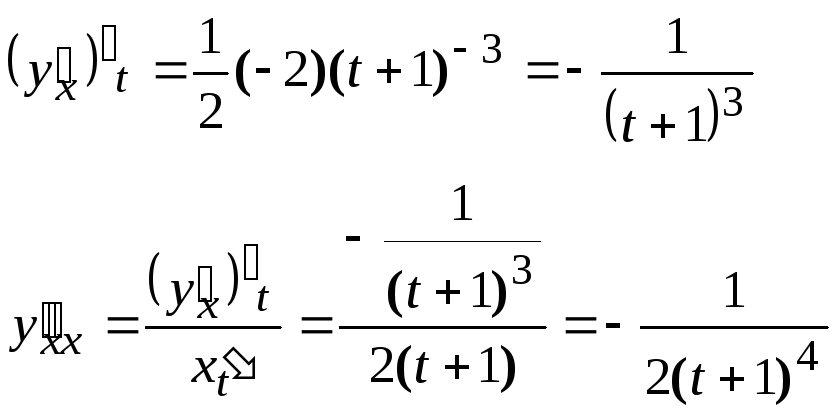
-
Касательная и нормаль к кривой
Если плоская кривая отнесена к
прямоугольной системе координат, то
уравнение касательной и нормали к ней
в точке
![]() имеют вид:
имеют вид:
 ,
где
,
где
![]() - значение в точке
- значение в точке
![]() производной
производной
![]() из уравнения кривой.
из уравнения кривой.

Найти уравнение касательной и нормали
к эллипсу
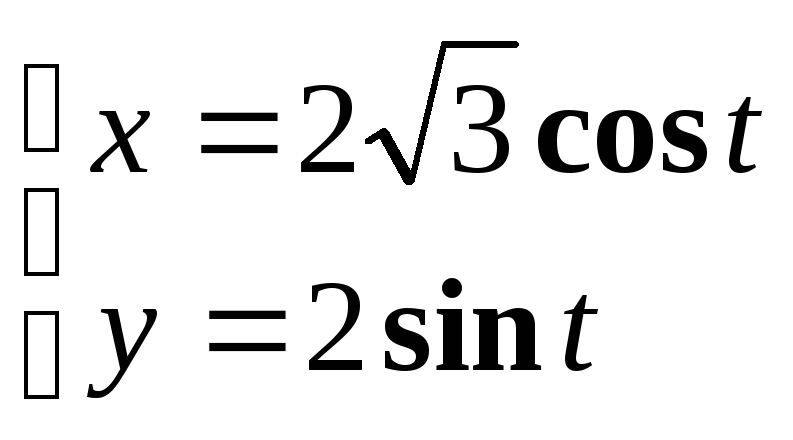 в точке, где
в точке, где
![]() .
.
Решение:
При
![]() ,
,
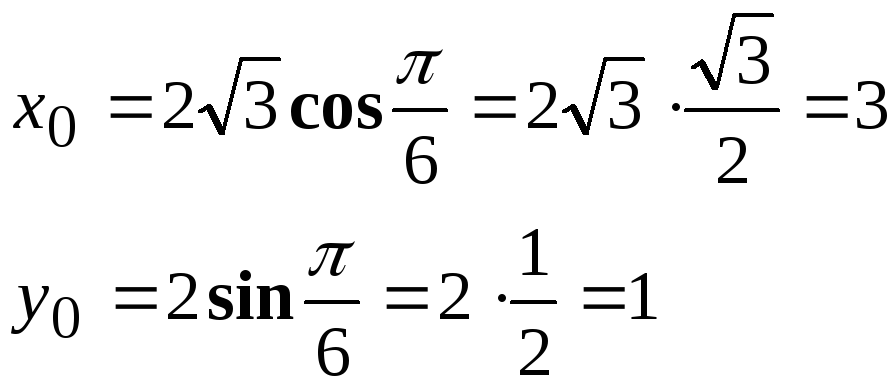 ,
получаем точку
,
получаем точку
![]()
Найдем
![]()
При
![]() ,
получаем
,
получаем
![]() .
.
Уравнение касательной:
![]()
Уравнение нормали:
![]()
-
Теорема Ролля, Лагранжа и Коши.
Теорема Ролля
Если функция
![]() :
:
-
непрерывна на отрезке [a, b]
-
имеет конечную производную в каждой точке интервала (a, b)
-
принимает равные значения на концах отрезка,
 ,
то в интервале (a,
b) существует по
крайней мере одна точка с, в которой
производная функции обращается в нуль:
,
то в интервале (a,
b) существует по
крайней мере одна точка с, в которой
производная функции обращается в нуль:
 .
.
Функция
![]() на концах отрезка [0, 4] принимает равные
значения
на концах отрезка [0, 4] принимает равные
значения
![]() .
.
Справедлива ли для этой функции теорема Ролля на отрезке [0, 4]?
Решение:
Найдем
![]() .
При
.
При
![]() ,
,
![]() не существует. Нарушено второе условие
теоремы Ролля.
не существует. Нарушено второе условие
теоремы Ролля.
Теорема Лагранжа.
Если функция
![]() :
:
-
непрерывна на отрезке [a, b]
-
имеет конечную производную в каждой точке интервала (a, b), то найдется по крайней мере одна внутренняя точка с интервала (a, b),
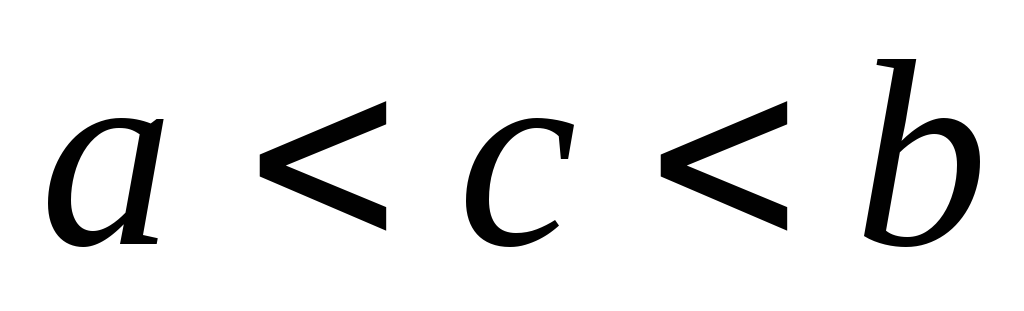 ,
для которой
,
для которой
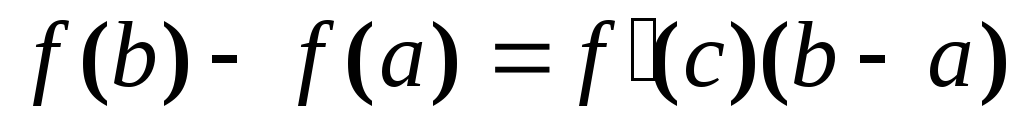 .
.
Проверить выполнение условий теоремы
Лагранжа для функции
![]() и найти соответствующее промежуточное
значение с.
и найти соответствующее промежуточное
значение с.
Решение:
Функция
![]() непрерывна и дифференцируема для всех
значений
непрерывна и дифференцируема для всех
значений
![]() ,
причем
,
причем
![]() .
Отсюда по формулам Лагранжа имеем
.
Отсюда по формулам Лагранжа имеем
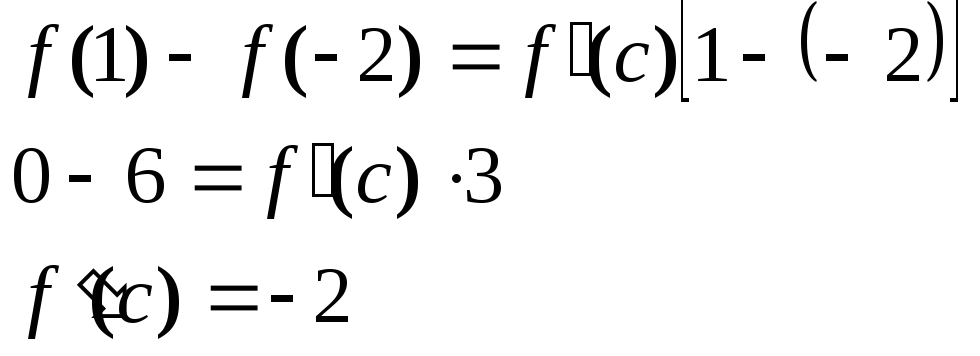
Следовательно,
![]() ;
годится только значение
;
годится только значение
![]() ,
для которого справедливо неравенство
,
для которого справедливо неравенство
![]() .
.
Теорема Коши.
Пусть функции
![]() удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
-
непрерывна на отрезке [a, b]
-
имеют конечные производные во всех точках интервала (a, b)
-
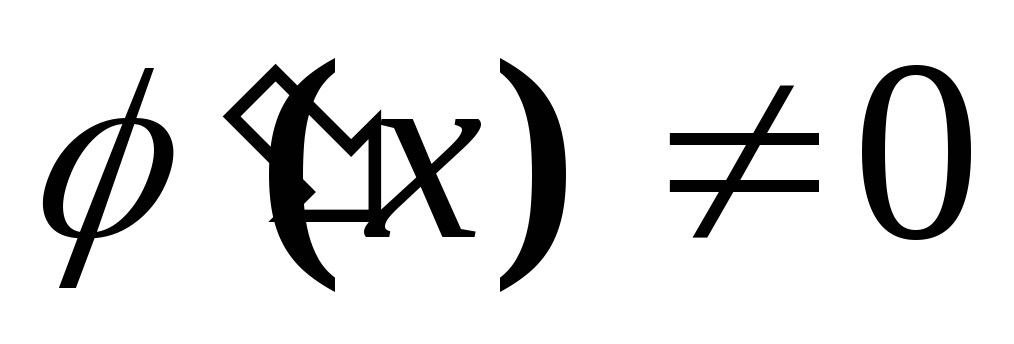 для любого
для любого
 ,
то внутри отрезка [a,
b] найдется такая
точка
,
то внутри отрезка [a,
b] найдется такая
точка
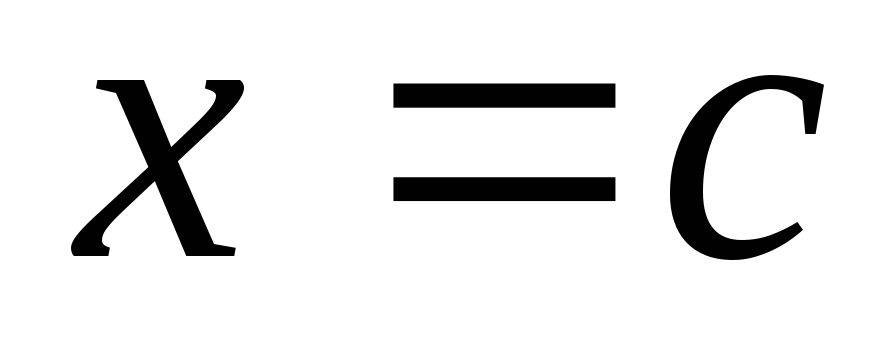 ,
,
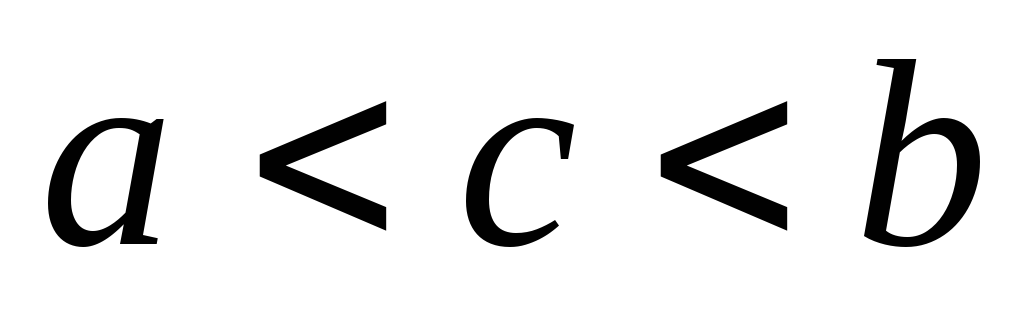 ,
что
,
что
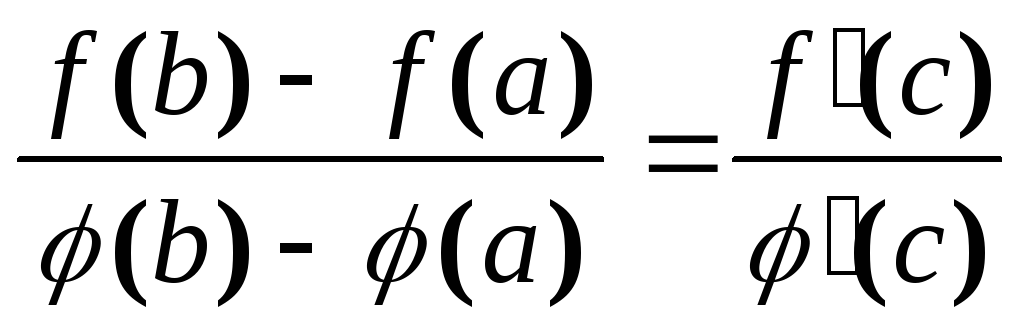
Проверить справедливость формулы Коши
для функций
![]() на отрезке [1; 2].
на отрезке [1; 2].
Решение:
Функции
![]() непрерывны и дифференцируемы при всех
значениях
непрерывны и дифференцируемы при всех
значениях
![]() .
Производные данных функций равны
соответственно
.
Производные данных функций равны
соответственно
![]() .
На отрезке [1, 2],
.
На отрезке [1, 2],
![]() .
.
Тогда между двумя значениями
![]() и
и
![]() существует значение
существует значение
![]() ,
удовлетворяющее равенству
,
удовлетворяющее равенству
![]()
![]() .
.
Вариант 1
