Построение центра и радиуса Кривизны
Определение центра и радиуса кривизны кривой m в заданной точке А выполняется в следующей последовательности:
1. На кривой по обе стороны от заданной точки отмечаем несколько точек.
2. Проводим из всех отмеченных точек полукасательные.
3. На полукасательных откладываем произвольные, но равные отрезки и через полученные точки проводим кривую.
4. Точке А заданной кривой соответствует точка A' построенной кривой. Проводим нормали к кривым в точках A и A'.
5. Точка пересечения нормалей 0 – центр кривизны кривой в точке А, а RA − радиус кривизны кривой в этой точке.
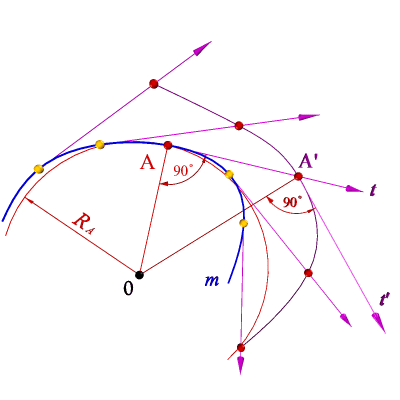
Множество центров кривизны кривой – это линия, которую называют эволютой данной кривой. Кривая по отношению к своей эволюте называется эвольвентой.
Свойства ортогональных проекций кривой
1. Проекцией кривой линии является кривая линия.
2. Касательная к кривой линии проецируется в касательную к ее проекции.
3. Несобственная точка кривой проецируется в несобственную точку ее проекции.
4. Порядок линии – проекции алгебраической кривой равен порядку самой кривой или меньше.
5. Число узловых точек (в которых кривая пересекает сама себя) проекции равно числу узловых точек самой кривой.
Случаи, когда плоская кривая проецируется в прямую (свойства 1, 4, 5), а касательная – в точку (свойство 2), не учитываются.
Рассмотрим три случая расположения окружности относительно плоскостей проекции.
Случай 1.
Окружность m лежит в плоскости || П1. Проекция окружности на П2 – отрезок, причем отрезок параллелен оси П2 / П1.
На плоскость П1 окружность проецируется в натуральную величину
Случай 2.
Окружность лежит
в плоскости 
П2
и под углом к плоскости П1. Проекция
окружности на П2 –
отрезок. Проекция окружности на П1 –
эллипс. Для уточнения формы эллипса
используем вспомогательные точки и
дугу радиусом данной окружности.
Случай 3.
Окружность лежит в плоскости общего положения. Обе проекции окружности –эллипсы.
Пространственные кривые линии
Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траектория движения точки.
Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.
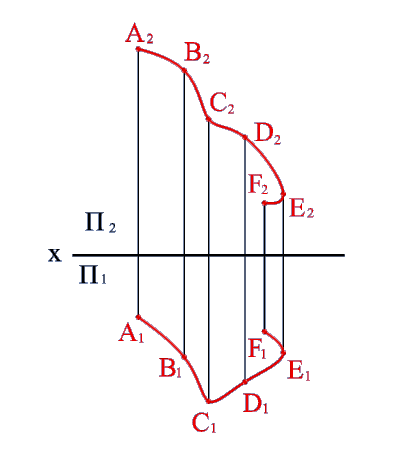
Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии
Цилиндрическая винтовая линия
Такую линию в пространстве описывает точка, которая движется по какой-либо образующей прямого кругового цилиндра, вращающегося вокруг своей оси так, что путь, проходимый точкой по образующей, пропорционален углу поворота цилиндра
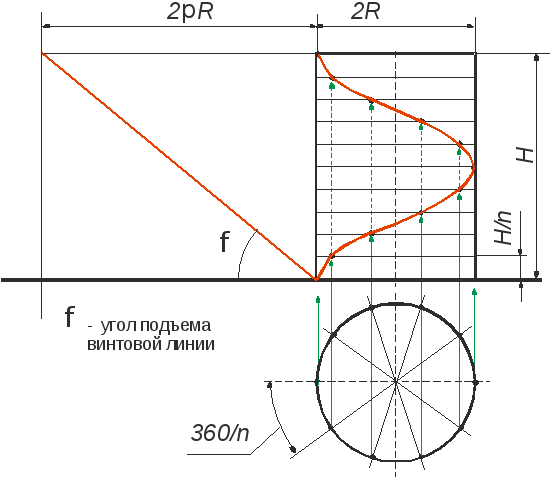
Смещение точки вдоль образующей за один оборот называется шагом цилиндрической винтовой линии. Различают правую и левую винтовые линии.
Горизонтальная проекция винтовой линии является окружностью, а фронтальная - синусоидой. На развертке цилиндрической поверхности винтовая линия изобразится в виде прямой. На рис.4 показан процесс формообразования винтовой линии.
Угол
называется
углом подъема винтовой линии. Этот угол
равен углу наклона касательной t в любой
точке винтовой линии к плоскости,
перпендикулярной ее оси. Цилиндрическая
винтовая пиния, подобно прямой и
окружности, обладает свойством
сдвигаемости.
Свойство сдвигаемости состоит в том, что каждый отрезок линии может сдвигаться вдоль нее, не подвергаясь деформации. Это свойство винтовой линии лежит в основе работы винтовых пар (винт-гайка). Винтовая линия является геодезической на цилиндрической поверхности.
Геодезической называется линия, принадлежащая поверхности и кратчайшая из всех линий, которые можно провести между двумя точками поверхности. Кроме цилиндрической винтовой линии, геодезическими линиями также являются прямая на плоскости, окружность большого круга на сфере и др.
Геодезическая линия изображается на развертке поверхности в виде прямой линии.