Лекция 4

МНОГОГРАННЫЕ ПОВЕРХНОСТИ. МНОГОГРАННИКИ

Поверхность, образованная частями попарно пересекающихся плоскостей, называется многогранной. На рис. 1 изображены виды многогранных поверхностей. Многогранная поверхность называется пирамидальной, если все ее ребра пересекаются в одной точке - вершине (рис.1, а). Многогранная поверхность называется призматической, если все ее ребра параллельны между собой (рис.1.б).

Рис.1. Изображение многогранных поверхностей, а - пирамидальной, б – призматической.

Элементами многогранных поверхностей являются грани, ребра и вершины. Отсеки плоскостей, образующие многогранную поверхность, называются гранями, линии пересечения смежных граней - ребрами, точки пересечения ребер - вершинами.

Геометрическое тело, со всех сторон ограниченное плоскими многоугольниками, называется многогранником. Простейшими многогранниками являются пирамиды и призмы. Среди других видов многогранников следует выделить - призматоиды и правильные многогранники (тела Платона). Призматоидом называется многогранник, у которого верхнее и нижнее основания - многоугольники, расположенные в параллельных плоскостях, а боковые грани представляют собой треугольники или трапеции (рис. 2).

Рисунок 2. Призматоид.

Существует пять правильных многогранников:

1. Тетраэдр (четырехгранник) - ограничен четырьмя равносторонними и равными треугольниками.

2. Гексаэдр (четырехгранник, или куб) - ограничен шестью равными квадратами.

3. Октаэдр (восьмигранник) - ограничен восемью равносторонними и равными треугольниками.

4. Додекаэдр (двенадцатигранник) - ограничен двенадцатью равносторонними и равными пятиугольниками.

5. Икосаэдр (двадцатигранник) - ограничен двадцатью равносторонними и равными треугольниками.

Вокруг всех правильных многогранников можно описать сферу.

Тетраэдр - правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это правильная треугольная пирамида).

Гексаэдр - правильный шестигранник (рис. 6.5.). Это куб состоящий из шести равных квадратов.

Октаэдр - правильный восьмигранник (рис.6.6.). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины.

Икосаэдр - состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины.

.   Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Звездчатый октаэдр - восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые "куски", внешние по отношению к октаэдру (рис. 6.9.). Это малые тетраэдры основания которые совпадают с гранями октаэдра. его можно рассматривать как соединение двух пересекающихся тетраэдров центры которых совпадают с центром исходного октаэдра. Все вершины звездчатого октаэдра совпадают с вершинами некоторого куба, а ребра его являются диагоналями граней (квадратов) этого куба. Дальнейшее продление граней октаэдра не приводит к созданию нового многогранника. Октаэдр имеет только одну звездчатую форму. Такой звездчатый многогранник в 1619 году описал Кеплер (1571-1630) и назвал его stella octangula - восьмиугольная звезда.

Малый звездчатый додекаэдр - (рис.6.10) звездчатый додекаэдр первого продолжения. Он образован продолжением граней выпуклого додекаэдра до их первого пересечения. Каждая грань выпуклого додекаэдра при продолжении образует правильный звездчатый пятиугольник. Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые "куски", внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра. При дальнейшем продолжении граней до нового пересечения образуется средний звездчатый додекаэдр - звездчатый додекаэдр второго продолжения. Последней же звездчатой формой правильного додекаэдра является звездчатый додекаэдр третьего продолжения - большой звездчатый додекаэдр. Он образован продолжением граней звездчатого додекаэдра второго продолжения до их нового пересечения

Точка на поверхности многогранника.

При построении проекций точек на поверхности (ребре или грани) многогранника необходимо следовать аксиомам принадлежности (принадлежность точке прямой и принадлежность точки плоскости). Проекции точек должны принадлежать соответствующим проекциям ребер. На рис.3 построены проекции точки D, принадлежащей профильному ребру SB боковой поверхности пирамиды. Проекция точки D₂ задана, для построения проекции D₁ используется вспомогательная прямая, которая параллельна ребру основания ВС.

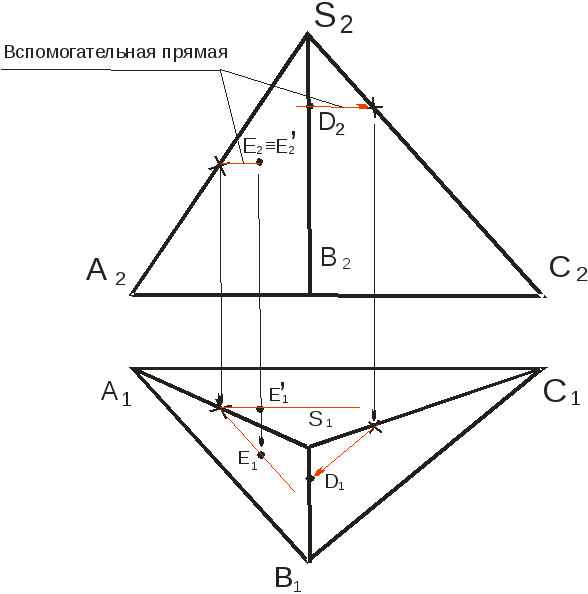
Рисунок 3. Точка на поверхности многогранника.

Точка Е принадлежит боковой поверхности пирамиды (Е₂ задана). По фронтальной проекции нельзя точно сказать, какой грани ASB или АSС, принадлежит точка, поэтому будем рассматривать две конкурирующие точки Е и Е^/. Для построения второй проекции точки Е (Е₁) проводятся вспомогательные прямые, параллельные ребрам основания АС и АВ.

Пересечение многогранника плоскостью

В результате пересечения многогранника с плоскостью получается ломаная линия. Вершины этой ломаной линии определяются на пересечении ребер многогранника и плоскости. Рассмотрим построение линии пересечения пирамиды с фронтально-проецирующей плоскостью  (рис. 4.). Линия пересечения на фронтальной плоскости проекций определена и проходит через точки 1₂, 2₂, 3₂ и 3₂`. Для построения второй горизонтальной проекции линии пересечения строим вторые проекции обозначенных точек, являющихся вершинами искомой ломанной, а затем последовательно их соединяем.

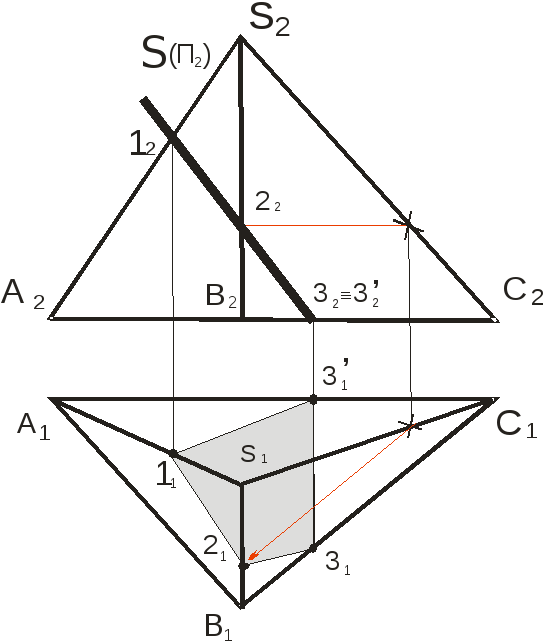
Рисунок 4. Построение линии пересечения пирамиды и проецирующей плоскости.

Рисунок 5. Наглядное изображение пересечения пирамиды и плоскости.

Пересечение многогранника с прямой.

Задача определения точек пересечения прямой линии с многогранником, сводится к нахождению точек пересечения прямой с плоскостями граней.

Алгоритм решения этой задачи, который рассматривался в одной из предыдущих лекций, начинается с того, что прямая заключается в проецирующую плоскость. Рассмотрим решение задачи на определение точек пересечения пирамиды и прямой m (рис. 6.).

1. Заключим прямую во вспомогательную фронтально-проецирующую плоскость ;

2. Построим линию пересечения пирамиды и вспомогательной плоскости по вершинам, которые находятся в точках пересечения ребер (1, 2 и 3);

3. Горизонтальная проекция линии пересечения (1₁, 2₁ и 3₁) и горизонтальная проекция прямой пересекаются в точках M₁ и N₁ , которые являются искомыми;

4. Строим фронтальные проекции точек M и N.

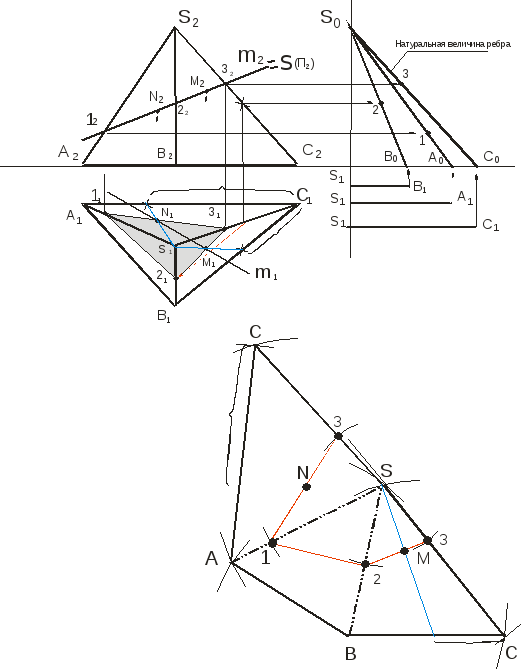
Рисунок 6. Построение точек пересечения пирамиды и прямой. Развертка пирамиды.

Развертка многогранника.

Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.

1. Длины двух соответствующих линий поверхности и ее развертки равны между собой;

2. Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;

3. Прямой на поверхности соответствует также прямая на развертке;

4. Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;

Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.

Существует три способа построения развертки многогранных поверхностей:

1. Способ нормального сечения;

2. Способ раскатки;

3. Способ треугольника.

При построении развертки пирамиды применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника - основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину ребер и сторон основания.

Построим развертку пирамиды, продолжив рисунок 6.

Определяем натуральные величины ребер основания методом плоско-параллельного перемещения. Построение развертки начинаем с грани ВSС. Для того чтобы нанести на развертку точки пресечения пирамиды с прямой, строим на развертке линию пересечения 1-2-3.

Для построения точек пересечения M и N на развертке воспользуемся вспомогательными прямыми, которые проведем из вершины пирамиды.