Лекция №5

кривые линии

общие определения и понятия

Все непрямые и не ломаные линии называются кривыми.

Кривая линия – это множество точек пространства, координаты которых являются функциями одной переменной.

В начертательной геометрии кривую рассматривают как траекторию, описанную движущейся точкой, как проекцию другой кривой, как линию пересечения поверхностей, как множество точек, обладающих каким-либо общим для всех их свойством, и т.д.

Способы задания кривой линии

• аналитический – кривая задана математическим уравнением;

• графический – кривая задана визуально на носителе графической информации;

• табличный – кривая задана координатами последовательного ряда точек.

Классификация кривых линий

Кривые линии могут быть закономерными, описанными уравнением, и незакономерными.

Закономерные кривые линии делятся на алгебраические, определяемые алгебраическими уравнениями (эллипс, парабола, гипербола и др.), и трансцендентные, определяемые трансцендентными уравнениями (синусоида, циклоида, спираль Архимеда и др.).

Важной характеристикой алгебраической кривой является ее порядок (трансцендентные кривые порядка не имеют). С алгебраической точки зрения порядок кривой линии равен степени ее уравнения, с геометрической - наибольшему числу точек пересечения кривой с прямой линией для плоских кривых и с произвольной плоскостью для пространственных.

Например, эллипс - кривая второго порядка, имеет уравнение x²/a² + y²/b² = 1 второй степени, пересекается с прямой максимум в двух точках. Прямую линию, имеющую уравнение первой степени ax + by + c = 0 (с произвольной прямой пересекается в одной точке), можно рассматривать как линию первого порядка. Кривыми второго порядка являются также окружность, парабола, гипербола.

Примерами кривых третьего порядка могут служить строфоида, Декартов лист, циссоида; четвертого - лемниската Бернулли, кардиоида, улитка Паскаля.

Начертательная геометрия изучает кривые линии и различные операции с ними по их проекциям на комплексном чертеже. Построение проекций кривой линии сводится к построению проекций ряда ее точек. В общем случае проекции кривой линии являются также кривыми линиями. Кривая линия определяется двумя своими проекциями.

Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими, остальные – пространственными.

Плоские кривые линии

 алгебраическая кривая 2-го порядка, прямая пересекает ее не более чем в двух точках.

Парабола

Гипербола

Эллипс

Синусоида – трансцендентная плоская кривая линия, получающаяся в результате двойного равномерного движения точки – поступательного и возвратно-поступательного во взаимно перпендикулярном направлении.

Кривые третьего и четвертого порядка

Все прямые и кривые второго порядка (окружности, эллипсы, параболы, гиперболы) являются частными случаями кривых третьего порядка.

Кривые третьего порядка

В общем случае уравнение кривой линии третьего порядка можно записать так: х³+а₁у³+а₂х²у+а₃ху²+а₄х²+а₅у²+а₆ху+а₇х+а₈у+а₉=0.

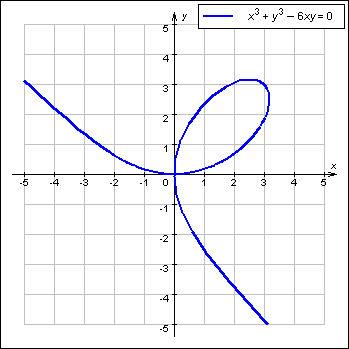
1. Декартов лист

Уравнение в прямоугольных координатах: x³ + y³ — 3аху = 0.

2. Строфоида (от греч. stróphos — кручёная лента и éidos — вид)

кривые четвертого порядка

1. Кардиоида (от греч. kardía — сердце и éidos — вид)

Кривая, описываемая какой-либо точкой М окружности радиуса а, катящейся без скольжения по неподвижной окружности того же радиуса. Уравнение в прямоугольных координатах: (x² + y² — 2ах)² = 4a(x² + y²); в полярных координатах: r = 2а (1 + cos j).

2. Лемниската Бернулли (от лат. lemniscatus, буквально — украшенный лентами)

Кривая, имеющая форму восьмёрки, уравнение в прямоугольных координатах:(x² + y²)² — 2a² (x² — y²) =0,

3. Улитка Паскаля

Уравнение в прямоугольных координатах: (x² + y² — 2Rx)² — а²(х² + y²) = 0,

4. Розы

Кривые, полярное уравнение которых:r = a sin mj; если m — рациональное число, то розы — алгебраическая К. чётного порядка. При m нечётном роза состоит из m лепестков, при m чётном — из 2m лепестков; при m рациональном лепестки частично покрывают друг друга.