Несобственный интеграл I рода
Пусть функция f (x) |
непрерывна |
при а х < |
+ . Тогда по |
|||||
определению полагают: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
f (x)dx. |
|
|
|
|
|
f (x)dx lim |
|
|
|
|
||
|
|
a |
b a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если предел существует, то несобственный интеграл называется
сходящимся; в противном случае расходящимся.
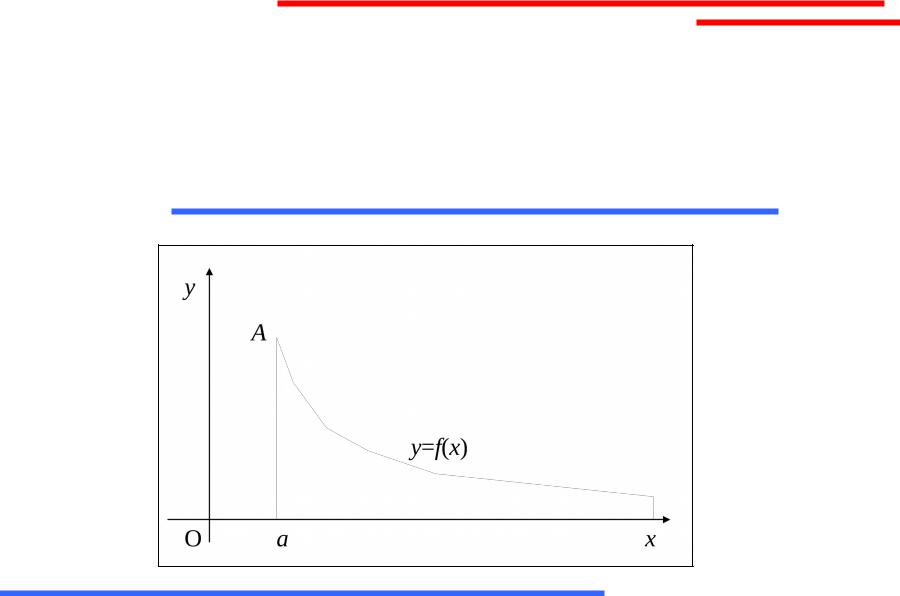
Несобственный интеграл I рода
Геометрически несобственный интеграл I рода представляет собой площадь криволинейной фигуры. ограниченной данной линией y = f (x), осью Ox и вертикалью х = а
Несобственный интеграл I рода
Пусть F(x) – первообразная функция для функции f (x):
F (x) f (x)
|
f (x)dx |
lim [F (b) F(a)]. |
|
||
a |
|
b |
|
|
Обозначим: F( ) lim F(b),
b
f (x)dx F ( ) F (a),
a
Пример:
|
|
dx |
|
|
|
|
|
|
|
arctgx |
|
|
|
|
|||
|
|
|
|
|||||
0 |
|
|
|
|
|
|||
1 x2 |
0 |
|
||||||
|
|
|
|
|
|
|||
; |
|
|
|
|
|
|
|
|
arctg( ) arctg0 |
|
|
0 |
|
||||
|
|
|
|
2 |
|
2 |
||
Теорема 1 (признак сравнения)
Если на промежутке [a; + ) непрерывные функции f (x) и (х) удовлетворяют условию 0 f (x) (х), то из сходимости интеграла
(x)dx
a
следует сходимость интеграла
|
|
f (x)dx |
|
|
|
|
|
||
|
a |
|
|
|
|
f (x)dx |
|
(x)dx ); |
|
(причем |
|
|||
a |
a |
|
|
|
|
Теорема 1 (признак сравнения)
а из расходимости интеграла
f (x)dx
a
следует расходимость интеграла
(x)dx
a
Замечание:
Для сравнения обычно используют интегралы вида:
dx , a 0, 0
a x
которые сходятся при > 1 и расходятся при 1.
–
.
Пример:
|
dx |
|
1 |
|
|
x2 (1 2x ) |
||
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
||
При х 1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||
x |
2 |
(1 2 |
x |
) |
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x |
|
|
dx |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dx |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
сходится (и < 1). |
||
1 |
|
|
|
|
|
|
|
|
|
x2 (1 2x ) |
||||||
|
x |
2 |
сходится |
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 2 (признак сравнения)
Если существует предел
то интегралы
f (x)dx и
a
lim f (x) k
x (x)
(f (x) > 0 и (х) >0),
(x)dx
a
ведут себя одинаково в смысле сходимости (т.е. одновременно сходятся или расходятся).
Пример:
|
x |
2 |
2 |
|
ln |
|
dx |
||
|
|
|
||
1 |
x2 1 |
|||
Решение:
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
||||||
|
dx |
|
|
|
ln |
x |
|
2 |
|
|
|
ln 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
x2 |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
– 1 |
1 |
сходится; |
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|||||||||||||
x2 |
lim |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
lim |
|
|
1 |
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
|
|
|
|
x |
|
|
|
1 |
|
|
|
x |
|
1 |
|
|
|
|||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
x2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x |
2 |
2 |
|
|
ln |
|
dx |
сходится |
||
|
|
|
|||
1 |
x2 1 |
|
|||