Определенный интеграл
1.Задача о вычислении площади криволинейной фигуры.
2.Задача о нахождении пройденного пути точки по заданной скорости .
3.Общее понятие определенного интеграла.
4.Свойства определенных интегралов.
5.Правила интегрирования.
6.Несобственные интегралы.
7.Понятие о приближенном вычислении определенных интегралов
? 1. Задача о вычислении площади криволинейной фигуры
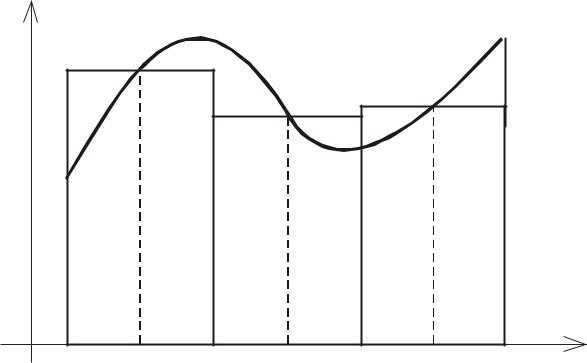
Задача о вычислении площади |
|||||||
криволинейной фигуры |
|
||||||
y ( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
y = f ( x ) |
|
|
|
A |
|
|
|
|
|
|
|
0 а = х 0 |
|
x 1 |
|
x 2 |
|
x n = b |
х |
|
|||||||
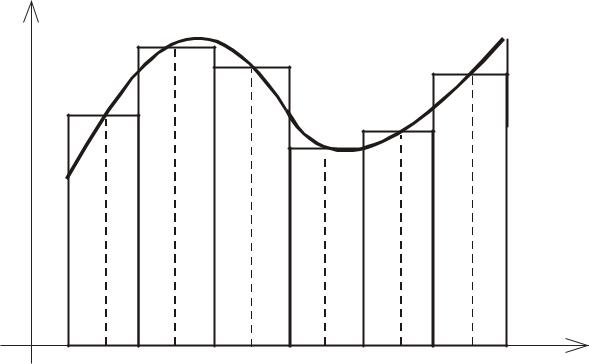
Задача о вычислении площади |
|
|||||||
|
криволинейной фигуры |
S |
0 |
f ( |
) x |
|||
y |
( x ) |
|
|
|
|
0 |
0 |
|
|
|
|
( x0 x1 x0 ) |
|||||
|
|
|
|
B |
||||
|
|
|
|
|
|
|
|
|
|
|
|
y = f ( x ) |
|
S1 f ( 1 ) x1 |
|||
|
|
|
|
|
|
|
( x1 x2 x1 ) |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
S j f ( j ) x j |
|||
|
|
|
|
|
|
( x j x j 1 x j |
||
0 |
а = х 0 |
x 1 x 2 |
|
n - x n = b |
х |
|
|
|
|
|
|
|
|||||
Sn f ( 0 ) x0 f ( 1 ) x1 ... f ( n 1 ) xn 1 |
|
|||||||
n 1 |
|
|
|
|
|
|
|
|
Sn f ( j ) x j |
|
( x j x j 1 x j ) |
|
|||||
0 |
|
|
|
|
|
|
|
|
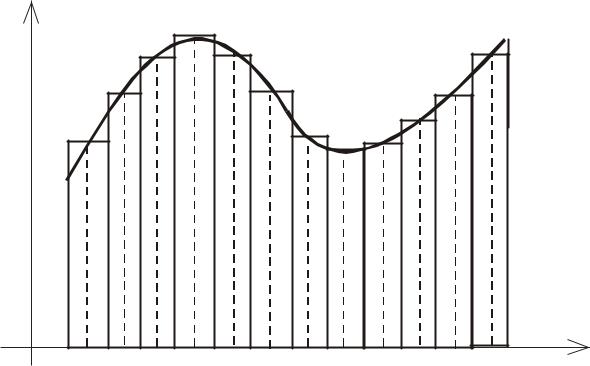
Задача о вычислении площади |
||||
|
криволинейной фигуры |
|
||
y ( x |
) |
|
|
|
|
|
|
B |
|
|
|
|
y = f ( x ) |
|
A |
|
|
|
|
0 а = х 0 x 1 x 2 x 3 |
|
n - x n = b |
х |
|
|
|
|||
|
S lim |
n 1 |
f j x j |
|
|
max x j 0 |
|
|
|
|
|
j 0 |
|
|
? 2. Задача о нахождении пройденного пути точки по заданной скорости
Задача о нахождении пройденного пути точки по заданной скорости
при равномерном движении
S
|
|
|
|
t0 |
T |
||
t
S V t
Задача о нахождении пройденного пути точки по заданной скорости
при неравномерном движении
Sj
tj
S j V ( j ) t j
n 1
S v( j ) t j
j 0
Задача о нахождении пройденного пути точки по заданной скорости
при неравномерном движении
S lim |
n 1 v j t j |
max t j 0 |
|
|
j 0 |
T
S v(t)dt
t0
