Многокритериальные задачи

Задача называется многокритериальной, если оценка варианта выбора ведется не по одному, а по двум или более критериям.

Ясно, что по каждому критерию в отдельности можно найти наилучший вариант выбора, однако практически всегда это будут различные элементы выбора. Поэтому необходимо обсудить разумную стратегию поведения ЛПР в этой ситуации.

Многокритериальный выбор оборудования

Перед ЛПР, действующего в производственной сфере, часто возникает задача выбора оборудования, наилучшим образом соответствующего имеющейся производственной задаче.

Выбор оборудования всегда является многокритериальным. Специфика такого выбора состоит в неизбежности применения той или иной схемы компромисса между критериями. Однако определение схемы компромисса является важной, но вторичной задачей, поскольку первичная проблема состоит в отборе критериев, адекватных решаемой производственной задаче.

По-видимому, не существует универсального набора критериев, пригодного для решения всех задач данной предметной области. Поэтому важно иметь достаточно широкий набор критериев, из которого в конкретных условиях может быть выбрано нужное подмножество критериев, адекватное решаемой задаче.

Таким образом, выбор наилучших вариантов оборудования сводится к трем последовательным выборам: выбор критериев, выбор схемы компромисса, непосредственный выбор вариантов оборудования.

Добавим здесь следующий грустный факт: в этом многоступенчатом процессе очень многое неизбежно носит субъективный характер.

Множество Парето

В таблице 1 приведен пример трехкритериального выбора

Таблица 1.

Здесь строки, отмеченные греческими буквами, соответствуют вариантам выбора, а столбцы- значениям критериев Ф₁, Ф₂, Ф₃

Будем считать, что все критерии максимизируемые. Нетрудно видеть, что варианта, который по всем критериям был бы наилучшим, нет.

Однако сравнивая попарно строки этой таблицы, мы можем заметить, что две строки могут быть сравнимыми, либо несравнимыми.

Две строки (а следовательно и два соответствующих варианта выбора) назовем сравнимыми, если все компоненты одной из них больше или равны соответствующих компонент другого.

У несравнимых строк (то есть не являющихся сравнимыми) найдется пара компонент, для одной из которых большей будет значение первой строки, а для другой – второй.

В таблице 1 сравнимыми, например, являются варианты и, а несравнимымии.

Для двух сравнимых вариантов могут возникнуть две ситуации.

Во первых, их строки могут полностью совпадать. Это значит, что соответствующие варианты неразличимы с точки зрения выбранного набора критериев. В этом случае мы будем рассматривать в дальнейшем любую из них, а вторую выбросим из рассмотрения и из таблицы. Правда такая ситуация довольно редкая. Нет ее и в нашем случае.

Во вторых, как в случае вариантови, один из сравнимых вариантов (у нас это) превосходит другого хотя бы по одному из критериев. Понятно, что в дальнейшем нет смысла рассматривать заведомо худший вариант из этой пары (у нас это). Поэтому вычеркнем его строку из таблицы.

После того, как всевозможные вычеркивания будут произведены, в таблице останутся только взаимно несравнимые варианты, а из ранее сравнимых останутся только лучшие.

Соответствующее множество вариантов называется множеством Парето.

В нашем случае это множество Соответствующие строки приведены в таблице 2.

Таблица 2

Значение множества Парето состоит в следующем.

Сложный выбор, и , частности многокритериальный, редко позволяет обоснованно выбрать единственный вариант. Процесс выбора – это часто всего лишь сужение области выбора.

Множество Парето – это максимальное сужение множества выбора до такого множества, внутри которого невозможно обосновать преимущества одного варианта перед другим, исходя только из критериальных оценок. Дальнейшее сужение возможно только либо за счет введения иерархии критериев, либо за счет введения некоторой схемы компромисса между ними.

Унификация (нормализация) критериев.

Некоторые их критериев, являются относительными, т. е. безразмерными величинами, заключенными между двумя крайними значениями 0 и 1. Такие критерии называются нормализованными или унифицированными.

Однако большинство критериев являются обычными физическими величинами, имеющими свои единицы измерения и диапазоны изменения. При этом некоторые из них являются максимизируемыми, другие – минимизируемыми. Помимо этого, существуют критерии, которые не выражаются непосредственно в числовой форме. Наконец, некоторые параметры, не оптимизируемые при проектировании, могут быть ограничены снизу, сверху или снизу и сверху одновременно.

Рассматриваемые ниже схемы при многокритериальном отборе вариантов предполагают, что наиболее удобной является унифицированная форма критериев. Унифицированными в данном контексте будем понимать критерии которые безразмерны, принимают значения между 0 и 1, максимизируемые (т. е. более предпочтительны с точки зрения данного критерия варианты, имеющие большее значение этого критерия).

Рассмотри одну из методик унификации критериев и ограничений.

Унифицированное значение произвольного максимизируемого критерия, для которого известны максимальное и минимальное значенияна произвольном варианте выбораопределяется так:

(1)

Для аналогичного минимизируемого критерия формула имеет вид:

(2)

Для критериев, формулируемых на обычном языке, унификация может быть произведена с помощью лингвистических переменных или экспертных оценок , о которых речь пойдет во второй части курса и в курсе «Системы искусственного интеллекта».

Наконец, для параметров, задаваемых в виде ограничений, используется следующая методика. Пусть допустимые значения критерия ограничены сверху величиной, т. е.

(3)

С учетом возможных погрешностей расчетов значений критерия для некоторых вариантов выборавыполнение неравенстване гарантирует выполнение последнего требования. Пусть- верхняя оценка погрешности вычисления для критерия. Положим

(4)

Тогда выполнение неравенства безусловно гарантирует выполнение требования (3).

Для тех вариантов , для которых

,…………………

положим

. (5)

При этом

(6)

Для ограничения снизу вида аналогично положим

(7)

и

(8)

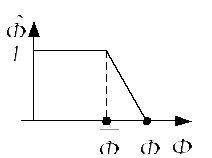
Унификация ограничения сверху

Унификация ограничения снизу

Здесь дана графическая интерпретация унификации ограничений

Пусть теперь критерий имеет интервальные ограничения вида:

, (9)

где и- нижняя и верхняя границы.

Вновь вводя величину предельной погрешности расчета , положим для произвольного варианта вывода:

(10)

Унификация двухстороннего ограничения